基于BO-SVM算法的钢板混凝土墙高速冲击损伤模式预测模型

陈沛涵,赵唯以

(青岛理工大学 土木工程学院,青岛 266525)

钢板混凝土(SC)墙是由钢板和混凝土通过连接件连接而成的组合结构。SC墙的外部钢板代替了传统钢筋混凝土(RC)墙的钢筋,并通过连接件和内部素混凝土相连。这一结构充分发挥了钢材抗拉和混凝土抗压的性能,使其具有承载力高、密闭性好、施工便捷等优点。同时,SC墙的抗冲击性能也十分出色,相比RC墙,SC墙防止击穿所需厚度可大幅降低,因此在核电厂房、防护结构等工程中得到了广泛应用[1]。

在导弹、飞机等的冲击作用下,结构可能发生局部损伤,甚至贯穿破坏。大量RC墙的高速冲击试验表明,即使墙体未发生贯穿,背冲击侧混凝土也会在冲击波的作用下开裂、飞射,严重威胁内部人员、设备的安全。而使用钢板包覆混凝土是一种有效的加固措施,WALTER等[2]、BARR[3]、TSUBOTA等[4]的高速冲击试验表明,在背侧布置钢板可以有效防止混凝土震塌破坏,提高墙体的抗冲击性能。

MIZUNO等[5-7]对SC墙在飞机模型撞击作用下的受力性能进行了试验研究和数值模拟,与以往RC墙的试验结果相比,SC墙防止击穿所需的厚度可以降低30%。SADIQ等[8]、LIU等[9]、BRUHL等[10]对MIZUNO等的试验建立了LS-DYNA有限元模型,并一致认为Mat_084(Winfrith模型)可以更好地模拟混凝土在高速冲击下的力学行为。HASHIMOTO 等[11]对12片RC墙、24片半SC墙以及4片SC墙在导弹撞击作用下的受力性能进行了试验研究,并基于能量原理提出了弹头速度与变形之间的计算式。研究结果表明,在不同的冲击速度下,半SC结构或SC结构的局部破坏表现为四种形式,如图1所示:(a)冲击物侵入目标;(b)目标背冲击侧混凝土崩落造成钢板鼓起;(c)冲击物撕裂背侧钢板;(d)冲击物贯穿目标。

图1 局部损坏效果[11]

结构在高速冲击下的破坏机理较为复杂,因此在设计中多采用经验公式计算侵彻深度或冲击物贯穿结构的临界速度。例如,基于大量RC墙的试验现象和数据,已有多个计算侵入深度或是防止目标贯穿所需厚度的经验公式[12]。针对SC墙,BARR[3]以等效配筋率考虑背侧钢板对结构抗冲击性能的贡献,提出了冲击物的穿透速度经验公式。WALTER等[2]、GRISARO等[13]将背侧钢板折算为一定厚度的混凝土,并按照RC墙计算防止穿透所需要的板厚。BRUHL等[10]根据已有文献中的高速冲击试验汇编了数据库,并在混凝土和钢板的穿透经验公式的基础上提出了SC结构抗冲击的三步设计法,该方法目前已被美国AISC N690s1-15规范[14]建议采用。KIM等[15-17]通过不同尺度SC墙的冲击试验对局部损伤模式进行了研究,结果表明三步设计法具有一定的保守性。

上述研究对SC墙局部损伤的计算均采用了经验公式法,而这些经验公式所使用的传统拟合方法需要预先假定某种特定的非线性函数形式,再确定函数中的待定参数,其计算结果往往偏保守。BRUHL等[10]利用三步法对130组被导弹冲击的SC墙进行损伤判别,其中有61组未被穿透的试件被偏保守地预测为穿透,总体准确率仅为51.5%。面对这样的强非线性问题,使用机器学习方法具有一定的优势。本文基于贝叶斯优化(BO)和支持向量机(SVM)算法,建立了高速冲击下SC墙局部损伤模式的BO-SVM分类模型,并通过F1得分、G-mean值、分类准确率评价模型的预测精度。研究结果表明,BO-SVM模型能够快速、准确地预测SC墙的冲击局部损伤模式,其预测精度优于传统计算方法,且优于K临近(KNN)和随机森林(RF)等其他常用机器学习算法。

1 研究方法

1.1 SVM算法

SVM算法建立在Vapnik-Chervonenkis维理论和结构风险最小原理的基础上,能保证找到的极值解是全局最优解而非局部最小值。因此,SVM算法能够避免过拟合,对未知样本有较好的泛化能力,可以很好地解决工程中的分类问题,但SVM算法具有较多的超参数,且超参数的调整直接影响模型的分类准确率,需对超参数进行反复调试才能得到最优的SVM模型[18]。

在现实问题中,输入参数和输出值之间通常具有高度的非线性。因此,需要利用非线性函数将数据映射到高维特征空间中,然后在高维特征空间中构建一个最优超平面,使所有数据点到该超平面的距离最大。超平面可以表示为

f(x)=wφ(x)+b

(1)

式中:φ(x)为非线性映射函数;w为权重;b为偏置。

如图2所示,在SVM模型中,假设f(x)与目标输出值y之间的差别绝对值大于ε时,均为预测正确。只有当误差小于ε时,才计算损失。ε-不敏感损失函数可表示为

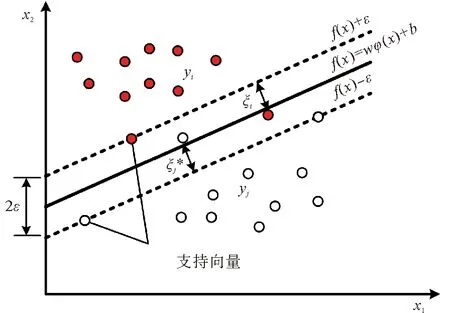
图2 SVM模型

(2)

为使所有数据点到超平面的距离大于一定的值,根据风险最小原理可得:

(3)

式中:C为惩罚参数;N为训练集样本个数。

(4)

限制条件为

(5)

该优化问题的目标函数为二次函数,限制条件为线性不等式,可以构造Lagrange函数,并转化为对偶问题,解得

(6)

使用核函数可以避免在高维空间中进行内积计算。常用的核函数包括线性核函数、多项式核函数、高斯径向基核函数等。

1.2 KNN算法

KNN是一种常用的有监督学习算法[19],为了判断未知样本的类别,KNN算法按照某种距离模式对未知样本与训练样本之间的距离进行计算,选择与未知样本距离最小的k个样本作为其k近邻,并根据未知样本的k个最近邻判断预测样本的类别。KNN方法计算简单且易于实现,对处理不规则数据的分类问题具有足够精度,但该方法高度依赖数据样本的精度,若样本中存在错误数据,会直接影响其准确率。

1.3 RF算法

随机森林(RF)属于集成学习的一种[20],其核心思想是以决策树为基学习器构建Bagging集成,并在决策树的训练过程中引入随机属性选择。随机森林具有结构简单、容易实现、计算开销小等优点,但对于小样本数据或特征较少的数据,可能不能产生较好的分类。对于分类问题,其分类精度通常与基学习器的数量选择有关。RF算法除了可以进行分类外还可以对参数进行灵敏度分析,通过每个特征在随机森林中决策树上的贡献值从而比较不同特征对最终结果的贡献程度。

1.4 贝叶斯优化算法

贝叶斯优化(BO)算法是一种常用的模型超参数优化方法[21]。假设一组超参数的组合为X=x1,x2, …,xn,不同的超参数组合会使模型取得不同的效果,而贝叶斯优化的目的则是选择出使SVM模型效果最好的超参数。

贝叶斯优化可以转化为如下问题:存在一个函数f(x),需要找到一个x∈X,使

(7)

式中:x为超参数。

由于并不能判断函数f(x)的凹凸性,所以需要基于序列模型求解问题,其算法如下:

第一步:确定函数f(x)、超参数搜索空间X和采集函数S[22]。

第二步:确定数据集D,该数据集中每一对数组表示为(x,y),x是一组超参数,y表示超参数对应的输出结果。

第三步:对数据集D拟合得到模型M,并求出模型的具体函数表示。

ρ(y|x,D)=FITMODLE(M,D)

(8)

第四步:求出使S(x,p)取得最大值所对应的变量点x(或x的集合),即

(9)

xi即为采集函数选择出的一组超参数。

第五步:将xi代入函数f(x)中,得到输出值yi。

第六步:更新数据集D。

D=D∪(xi,yi)

(10)

第七步:返回第三步,继续选择超参数x,循环T次停止。

1.5 SMOTE算法

为了解决数据集不平衡的问题,本文采用了SMOTE过采样技术。SMOTE算法是CHAWLA等提出的一种过采样算法[23],如图3所示,该算法将少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中,可有效解决少数样本量过少的问题,但是SMOTE算法在扩大数据规模的同时增加了模型训练的复杂度,会导致模型训练时间的增加。其生成新样本的过程如下:

图3 SMOTE采样原理

1) 对于少数类样本集中每一个样本x,以欧氏距离为标准计算它到所有样本的距离,得到其k近邻。

2) 根据样本不平衡比例设置一个采样比例以确定采样倍率N。

3) 随机选择k近邻中的一个进行线性插值,进而合成少数类样本。其合成公式为

xnew=x+rand(0,1)×|x-y|

(11)

式中:x为少数类样本;y为近邻样本。

1.6 BO-SVM模型

机器学习算法中的超参数往往决定着模型最终的性能,而传统的机器学习模型往往只能通过试错法来确定其超参数。本文提出的BO-SVM模型,主要通过BO算法优化SVM模型的3个超参数以及SMOTE算法平衡样本数据,所优化的3个超参数分别为K(Kernel)、C和G(Gamma)。其中,K为决定SVM核函数类型的超参数;C为惩罚参数,影响着SVM分类器对数据分类的严格程度;G为选用RBF作为核函数后自带的一个参数,决定了数据映射到新的特征空间后的分布,当选用RBF以外的核函数时,不赋予G值。

使用Python语言建立BO-SVM模型。如图4所示,BO-SVM模型的算法主要包含七个步骤:

图4 BO-SVM模型建立过程

第一步:收集高速冲击下SC墙局部损伤模式数据。

第二步:对收集的数据进行5折交叉验证。在这一步骤中,SC墙数据被分为5个数据集,其中4个数据集用来训练,另1个数据集用来测试。整个交叉验证过程中,BO-SVM模型被训练和测试了5次。

第三步:对划分的训练集进行SMOTE过采样。

第四步:建立SVM模型作为基础模型。

第五步:使用BO优化SVM。对过采样后的训练集进行训练,寻找效果最好的模型对应的超参数。这一步骤使用BO算法对SVM模型的K,C和G3个超参数进行优化。其中,K的搜索范围为linear(线性核)、polynomial(多项式核)、rbf(高斯核)三种类型的核函数;C的搜索范围为[0.001, 1000];G的搜索范围为[0.001, 1000]。

第六步:使用获得的超参数构建最终的BO-SVM模型,并在测试集上进一步测试模型效果。

第七步:从第二步开始重复该过程,其中交叉验证过程生成另一个训练测试集。

1.7 模型评价指标

本文使用准确率(Accuracy)、F1得分(F1-score)和G-mean 3个指标来度量分类模型的性能。以上指标均需根据表1所示的样本混淆矩阵来进行计算。

表1 混淆矩阵

1) 准确率(Accuracy)。准确率可以衡量模型的整体分类效果,准确率越接近1,分类效果越好,其计算公式如下:

(12)

式中:A为准确率(Accuracy)。

2) F1得分(F1-Score)。F1-Score[24]为查准率(Precision)和召回率(Recall)的调和值。其中,Precision为正确预测为某类占全部预测为某类的比例,Recall为正确预测为某类占全部实际为某类的比例。F1-Score越接近1,分类效果越好,其计算公式如下:

(13)

(14)

(15)

式中:P为查准率(Precision);R为召回率(Recall);F为F1得分(F1-Score)。

3) G-mean[25]是各类样本召回率的几何平均值。相对于其他指标,G-mean对判别模型在少数类别上的判别效果更敏感,只有当各类样本分类精度均较高时,G-mean才会较大。G-mean越接近1,分类效果越好,对于多分类问题,其计算公式如下:

(16)

式中:M为各类样本召回率的几何平均值(G-mean)。

2 数据收集

本文在BRUHL等[10]汇编的130组样本组成的数据库基础上,增加了LEE等[15]、KIM等[16-17]和XU等[26]报道的试验样本。由于钢板撕裂破坏为冲击物恰好穿透试件且无残余速度的临界破坏模式,且该类别的试验样本较少,因此在研究中偏于保守地将其归类为贯穿破坏模式。同时,剔除仅含有前钢板的样本,最终数据库中共采集到163组样本。

2.1 高速冲击试验

数据库中的样本均为研究人员对钢板混凝土墙进行的高速冲击试验得到。如图5所示,冲击物由气枪射出,垂直射向钢板混凝土墙,通过高速摄像机记录整个碰撞过程。试验完成后,观察试件的局部变形和失效模式。表2提供了各研究人员通过高速冲击试验得到的3种损伤模式的样本数。

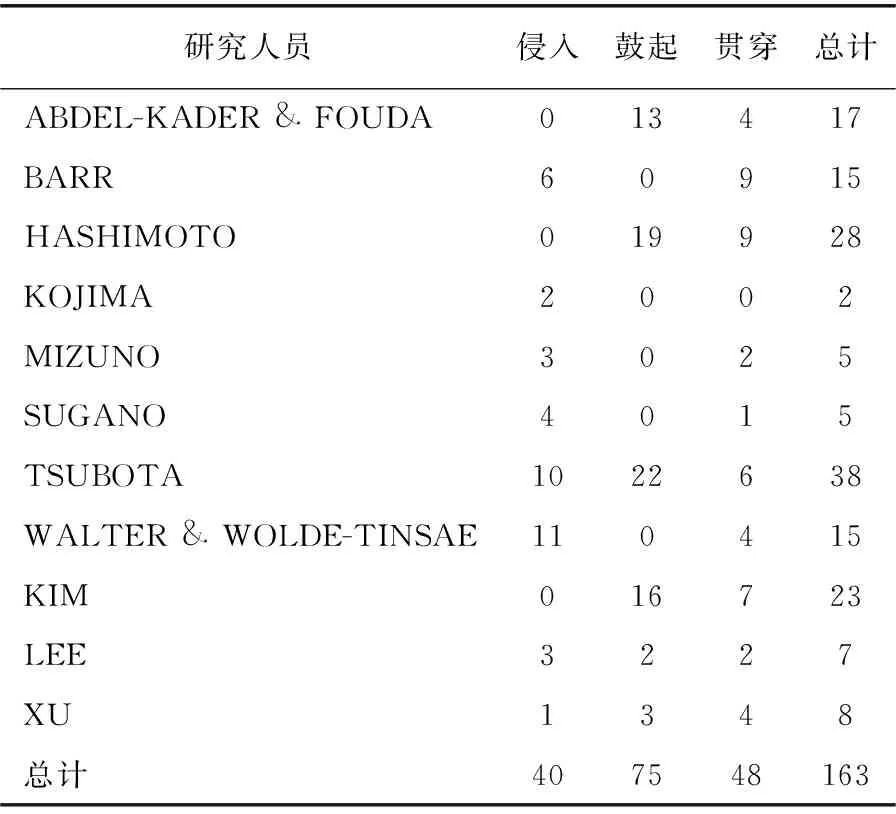
表2 数据库试验结果汇总[10,15-17] 组

图5 高速冲击试验装置

由表2可知,最终采集到的163组试验样本共包含3个输出类别:侵入——40组样本;鼓起——75组样本;贯穿——48组样本。输入包含10个特征,输入特征见表3。

表3 训练模型的特征描述

2.2 数据预处理

2.2.1 输入参数灵敏度分析

从现有的试验数据中共采集到如表3所示的10个输入参数,输入过多对结果贡献程度较小的参数可能会导致建立的机器学习模型产生过拟合现象,而以往的研究并未具体讨论各个输入参数对最终结果的影响程度,因此使用RF算法对模型输入参数进行灵敏度分析,并剔除对结果影响极小或者无关的参数。

如图6所示,根据RF算法分析得到的权重可知混凝土厚度Tc为影响SC墙损伤模式最重要的参数,其次,冲击初速度v0和混凝土抗压强度fc也是判断损坏模式的关键指标,这可以为高速冲击下的参数优化提供参考。同时,从图6中可以看出,每个输入参数都对结果有明显影响,因此不对输入参数进行剔除。

图6 模型各输入参数重要程度

2.2.2 数据过采样

从采集到的数据可以看出,各个类别的样本数量分布不均,损伤模式为侵入和贯穿的样本数明显少于损伤模式为鼓起的样本数。因对不平衡的数据集的分类预测会产生较大误差[27],往往会使预测结果偏向多数类,故采用SMOTE采样算法[28]对侵入类和贯穿类数据进行过采样,为少数类别生成更多的数据。同时,使用交叉验证将数据集分为5个部分,其中1个数据集用于性能评估,剩余4个数据集用于模型训练和选择,此过程有助于使模型产生更可靠的结果[29]。

3 结果与讨论

按照图4所示流程建立BO-SVM模型并与SVM(有过采样)模型、SVM模型、KNN模型和随机森林(RF)模型进行对比。为尽量降低模型误差,除BO-SVM模型以外的4个模型超参数均采用试错法进行选择。因此,由试错法选择的基础SVM模型K=’rbf’,C=20,G=4.6;在KNN模型中,邻居数k过小会导致过拟合,k过大会使整体模型变得简单,从而导致精度不够。经试错过程选择k_neighbors=10,p=1;RF模型的决策树数目ntree=500。最终所提出的BO-SVM模型K=’polynomial’,C=546,其余超参数与基础SVM模型相同。

3.1 F1-Score测试结果

5个模型的平均F1-Score结果见表4,可以看出BO-SVM模型的F1-Score为0.73,高于其他4个模型,这表明提出的BO-SVM模型具有较高的预测能力。

表4 不同模型评价指标结果

3.2 G-mean计算结果

由表4可以看出,BO-SVM模型的G-mean值为0.73,高于其他4个模型。SVM(有过采样)模型的G-mean值为0.60,大于SVM模型的0.55,这说明SMOTE过采样增加了SVM模型对正负类样本的判别效果。可以看出,BO-SVM模型无论是对多数类还是少数类样本,都有较好的判别效果。

3.3 准确率测试结果

由表4和图7可知,BO-SVM模型的平均分类准确率为74.23%,高于其他4个模型,表明取得最佳超参数的BO-SVM模型获得了较高的平均准确率。同时, SVM(有过采样)模型对于鼓起破坏模式预测精度低于SVM模型,但对于侵入类和贯穿类的预测精度均高于SVM模型,这是因为SMOTE过采样对少数类产生了一部分伪样本,从而影响其对多数类的判别,但也使SVM(有过采样)模型对少数类别预测的精度有所提高,使整个模型更加均衡。对比KNN模型和RF模型,RF模型的准确率优于SVM(有过采样)模型仅次于SVM模型,且RF模型对侵入类和贯穿类的预测精度较低,表明RF模型对少数类的预测效果较差。总的来说,尽管BO-SVM模型对鼓起类的预测精度略小于部分模型,但其平均精度仍然更高,且BO-SVM模型对3个损伤水平的准确性比其他模型更加均衡,这有助于更好地预测未知数据。

4 结论

1) 本文提出的BO-SVM模型平均准确率达到74.23 %,远优于传统的理论计算方法,优于包括未BO优化下的SVM(有和没有过采样)模型、KNN模型、RF模型在内的传统机器学习模型。

2) BO方法和SMOTE算法成功达到寻找模型最佳超参数和平衡模型样本的目的,使BO-SVM模型在F1-Score值(0.73)和G-mean值(0.73)方面实现了更高的损伤预测能力。

3) BO-SVM模型可用作实际设计中预测SC墙局部损伤水平的工具,特别是在初始设计阶段。

4) 利用随机森林算法初步分析了各输入参数对损坏模式影响的重要程度,为高速冲击下的参数优化提供参考。

5) 该研究仅限于考虑SVM模型的3个超参数,下一步应考虑对其他超参数优化以及更优秀的过采样技术提高模型性能。