基于人体感知模型的汽车驾驶模拟器动感模拟逼真度评估方法

熊 威，李 鹏，王晓蕾，吴婷婷

(南京林业大学汽车与交通工程学院，江苏 南京 210037)

0 引言

动感模拟平台的运动空间有限，一般单自由度平动运动范围为1.5 米左右，转动运动范围为40°左右，具体数值随构型和尺寸的不同而存在差异[1]。因此，如何在有限的运动空间内模拟实际车辆的运动便成为了关系到模拟逼真性和平台运动模拟能力的关键问题。动感模拟算法（又称洗出滤波算法、运动模拟策略等）正是为了解决这一问题而产生的，其目的就是在平台有限的运动空间内给车辆驾驶员以逼真的运动感受[2]。

动感模拟算法最早为飞行模拟器而研发，为使飞行员产生持续的运动体感，动感模拟平台在完成一次运动后，需要缓慢地返回中位，为下一次运动模拟做准备，实现这一过程的算法叫做洗出算法，又称体感算法，该算法被广泛使用，俗称经典动感模拟算法[3]。该算法的输入为车辆运动在车体坐标系下的线加速度和角速度，线加速度一部分经过高通滤波通道得到平台的线位移，高通滤波器将容易导致平合超限的低频信号滤除，主要模拟高频加速度信号，另一部分通过低通滤波器通道通过将平台倾斜，依据人体对运动的感觉机理，利用重力在倾斜方向上的分量模拟持续低频加速度，该通道叫倾斜协调通道，这种技术叫倾斜坐标技术[4]。角速度通过高通滤波器通道经变换后得到高频角位移，与倾斜协调通道的低频角位移叠加得到平台的总的角位移，由此实现了车辆运动到平台运动的变换。

洗出滤波算法最初是由Schmidt和Conrad提出[5]，之后由于学者多以此为基础进行研究，该算法又被称为经典洗出算法，它以形式简单、易于调节、执行速度快、反应速度快等优点得到广泛认可。1972 年Nahon基于经典洗出滤波算法提出了一种新的洗出滤波算法——自适应洗出滤波算法[6]，同经典洗出滤波算法和最优洗出滤波算法相比，三者在结构上基本相同，区别在于自适应洗出滤波算法的滤波器参数的可变性，即滤波器参数可根据输入信号的变化进行自适应调节，解决了经典洗出滤波算法和最优洗出滤波算法参数固定的问题，实现参数随输入信号实时改变，达到防止运动超限的目的，并尽可能使驾驶员获得更高逼真度的体感，而且自适应洗出滤波算法的代价函数相当灵活，能够根据实际需求添加相应的约束条件。王辉[7]分析了自适应洗出滤波算法输出随着输入增大而发散的原因，并确定了自适应滤波器系统稳定时的自适应权重、自适应步长与输入幅值需满足的关系。葛冠宇[8]在此基础上做了改进，并在模拟器上应用了改进后的自适应算法，实验证明该算法对提高运动临场感效果明显。王军政[9]的研究成果又表明2 阶的代价函数所模拟出的运动临场感更加逼真。闫剑锋[10]对自适应算法的稳定性做了研究分析，还提出了改进的自适应算法，较好的解决了模拟器可能超出运动极限的问题。我国目前对于动感模拟逼真度的研究同发达国家相比存在着不小的差距，存在着较难突破的瓶颈问题，但是发展的速度较快，不仅在关键技术上取得众多突破，而且许多研究成果已经广泛的应用于生产实践，取得了较好的经济效益。然而，当前的研究大多基于一些理论假设，缺少现实条件的约束，主要存在算法解算能力不强，模型尺寸优化效率低等问题，影响了研究成果的实用性。

本文首先建立人体感知模型作为模拟试验人体感知参数的评价标准，然后通过设置汽车工况试验对体感模拟算法进行了验证，包括加速试验，爬坡试验以及制动试验。通过对比每种工况下汽车模拟试验的输出感知参数与模拟器试验的输出感知参数可以得出，本文优化设计的洗出滤波算法能够有效的降低驾驶员模拟时的体感误差，提高驾驶模拟的逼真度，给予驾驶员更真实的驾驶感觉。

1 模拟流程及仿真模块搭建

模拟流程图如图1 所示，其中所建人体感知模型为相同感知模型。

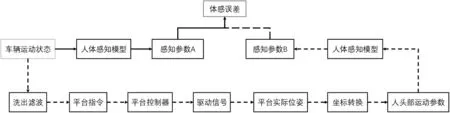
图1 模拟仿真流程图

洗出算法仿真如图2 所示，主要由三部分组成。第一部分为加速度的高通滤波器，该滤波器主要是用来模拟车辆产生的瞬时加速度；第二部分为加速度的低通滤波器，该滤波器主要用于模拟车辆产生的低频加速度信号；第三部分为角速度的高通滤波器，主要用于模拟车辆产生的高频角速度信号。由于模拟平台的空间有限，无法完全模拟低频加速度信号，于是采用倾斜协调的方式，利用重力和角度倾斜来模拟x，y 方向的低频加速度信号，第一部分和第二部分共同构成了加速度的模拟。

图2 输入模块

以加速度的高通滤波器为例解释自适应高通滤波器的实现：输入为三个方向的加速度信号，经过限幅信号后，与重力加速度相加，再经过坐标变换矩阵将车体坐标系转换到世界坐标系下，并减去重力加速度。将该信号输入到自适应高通滤波器中，输出得到输入给平台的加速度数据，并将其二次积分限幅后得到平台的位移。在自适应高通滤波器中，通过自适应算法，根据输出加速度信号，速度输出信号，位移输出信号和位移积分的加速度信号，实时变化自适应增益k。

2 建立人体感知模型

2.1 人体前庭系统

前庭系统是由半规管和耳石等多种组织构成的，它通过进行一系列复杂的物理化学变化，从而引起了人体的运动感知[11]。对于驾驶感知相关的研究而言，恰当的前庭系统模型对于实现动感模拟算法至关重要，动感模拟算法的好坏则直接取决于前庭模型的选用。

人体前庭器官的感觉阈值存在差异，同时耳石和半规管在各个方向上的运动感知灵敏度也有所不同，如表1所示。

表1 人体前庭器官感觉阈值

2.2 耳石模型

耳石的作用在于提供人体感受线加速度的信息，这种感知是通过感知毛细胞的运动来实现的[12]。直线运动和重力分量均可引发加速度，耳石感应到的加速度是相对加速度，如式⑴所示：

其中，f—人体前庭中心的输入比力，m/s2；a—人体的绝对加速度，m/s2；g—重力加速度，m/s2。

人体耳石模型如图3所示。

图3 人体耳石模型

耳石模型传递函数如式⑵所示：

耳石模型参数如表2所示。

表2 耳石模型参数

2.3 半规管模型

人体前庭系统中的半规管承担着感应空间中角速度的职责，其模型如图4所示。

图4 人体半规管模型

图4中，ω—人体前庭某方向的输入角速度，rad/s；—人体感受到该方向的角速度，rad/s；Ta、TL、TS—半规管模型的物理参数，无量纲；δTH—半规管感受器偏差阈值，rad/s。

半规管模型传递函数如式⑶所示：

半规管模型参数如表3所示。

表3 半规管模型参数

2.4 搭建感知模型仿真模块

感知参数A 模块如图5 所示，以人体感知A 为例，包含三个加速度方向和三个角速度方向一共六个方向的感知。由于洗出算法的输出是在世界坐标系下的，因此，首先将其通过变换矩阵转移到人体坐标系下，其中加速度通道叠加x，y方向的倾斜角对加速度的感知。在进行坐标变换后，将其引入人体耳石模型感知加速度，引入人体半规管模型感知角速度，最终得到人体感知的加速度和角速度。感知参数B的模块搭建与图6相似，只需舍弃坐标转换模块即可。

图6 输入加速度信号

3 动力性试验

3.1 加速试验

将输入信号设置为从0 开始的x轴方向的模拟加速度信号，加速段加速度为ax=2m/s2，持续时间为4s，输入加速度信号如图6所示，平台输出位移如图7所示。

图7 输出位移

感知参数A 与感知参数B 的输出如图8 所示，设定评价标准如式⑷所示，评价标准曲线如图9所示，其中设置10%为误差评价标准值。

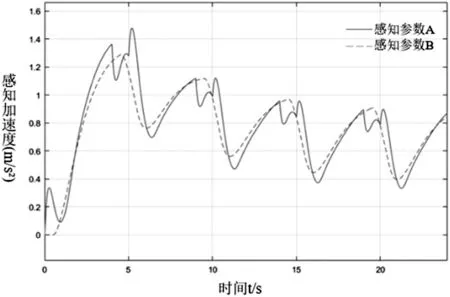
图8 人体感知参数输出图

图9 模拟准确性评价

由图7 可知，平台输出位移在加速的过程中逐渐减小，且动平台的最大输出位移0.21m 小于平台工作空间的边界限制1.15m，同时能够减少平台回到中位的时间。由图8可知，在模拟开始时，模拟器试验输出的人体感知参数与车辆模拟试验输出的人体感知参数二者之间的感知参数误差较大，随着模拟工况试验时间的进行，感知参数之间的感知参数误差逐渐减小，体感逼真度逐步提高。由图9可知，整个模拟过程中超出误差评定标准时间段共有2.2s，占据总模拟时间25s 的8.8%，加速试验的感知参数A 与B 的差值较小，在90%以上的试验持续时间内，差值与感知参数A变化值的比值百分比在10%以下，这表明动感模拟算法能比较准确地对人体的运动感觉进行模拟。

3.2 爬坡试验

将输入信号设置为2-2.5s 内短时间x 轴方向的模拟角速度信号ωx=0.05rad/s，输入信号如图10 所示，平台输出角度如图11所示。

图10 输入角速度信号

图11 输出角度

此时，感知参数A 与感知参数B 的输出如图12 所示，由于平台角度变化较为缓慢，故使用x方向的角速度通道来对比感知参数。自适应增益K的值会影响平台的输出角度，因此为了保证平台输出真实的角度，自适应增益K 值取1。评价标准如式⑷，评价标准曲线如图13所示。

图12 人体感知参数输出图

图13 模拟准确性评价

由图11可知，在2s时输入角速度信号之后平台角度会产生一个缓慢变化以此模拟车辆从平坦道路进入坡道的过程，且平台最大输出角度0.75rad不超过平台工作空间角度限制1.18rad。由图12可得，在模拟器模拟试验开始时存在0.2s 延时，而后随着模拟时间的进行，模拟器试验输出的人体感知参数与车辆试验输出的人体感知参数二者之间的感知参数误差减小，驾驶员体感逼真度逐渐提高。由图13可知，整个模拟过程中超出误差评定标准时间段共有2s，占据总模拟时间20s 的10%，爬坡试验的感知参数A 与B 的差值较小，在90%以上的试验持续时间内，差值与感知参数A 变化值的比值百分比在10%，这表明动感模拟算法能比较准确地对人体的运动感觉进行模拟。

4 制动性试验

将模拟输入信号设置为前24秒加速，加速段加速度为2m/s2，时间为4s，然后以-3m/s2的加速度减速，直至速度为0。输入信号如图14 所示，平台输出位移如图15所示。

图14 输入加速度信号

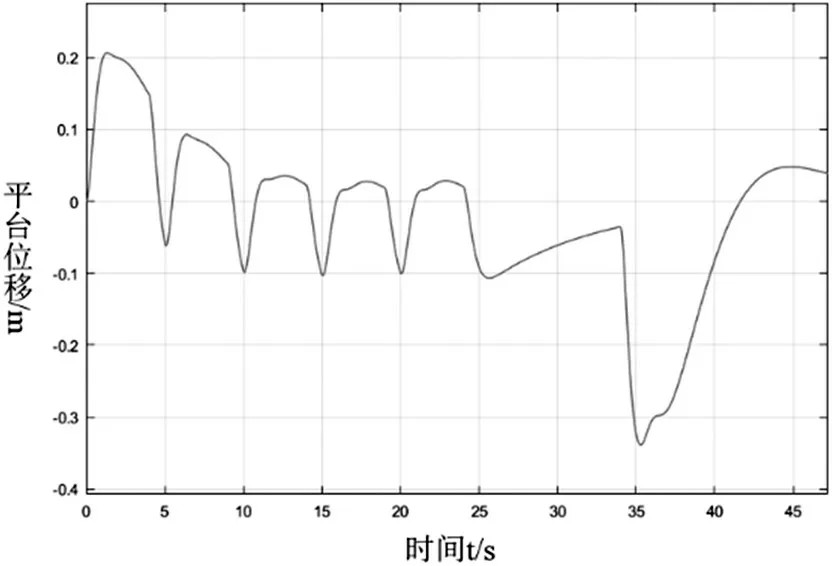
图15 输出位移

感知参数A与感知参数B的输出如图16所示。

图16 人体感知参数输出图

评价标准如式⑷，评价标准曲线如图17所示。

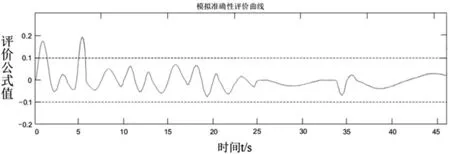
图17 模拟准确性评价

由图15可知，加速时间段平台输出位移与加速试验平台输出位移近乎相同，且最大输出位移0.21m 不超过平台工作空间位移限制1.15m。制动之前的十秒钟匀速模拟，34s 后输入制动加速度，使得平台输出位移有一个突变。图16表明，加速段人体感知参数的输出对比与加速试验基本一致；匀速时段感知误差近乎为0，模拟器输出的感知参数更低，便于能够更好的模拟制动；当输入制动加速度时，模拟器试验输出的人体感知参数与车辆试验输出的人体感知参数二者下降梯度几乎相同，但模拟器试验输出的人体感知参数下降更低，能更好地模拟汽车制动时的人体感知。由图17可知，整个模拟过程中超出误差评定标准时间段共有2.2s，占据总模拟时间45s 的4.8%，制动试验的感知参数A 与B 的差值较小，在90%以上的试验持续时间内，差值与感知参数A 变化值的百分比在10%以下，这表明动感模拟算法能比较准确地对人体的运动感觉进行模拟。

5 结束语

本文首先建立了人体感知模型作为驾驶模拟试验人体感知参数的评价标准，然后通过设置汽车典型工况试验对体感模拟算法进行了验证，其中包括了加速试验，爬坡试验以及制动试验。通过对比每种典型工况试验下汽车模拟试验的输出感知参数与模拟器试验的输出感知参数可以得出，本文所采用的洗出滤波算法能够有效的降低驾驶员模拟时的体感误差，提高驾驶模拟的逼真度，给予驾驶员更真实的驾驶感觉。