一种基于新移动策略的灰狼优化算法*
张 军,代永强,施秋红
(1.甘肃农业大学信息科学技术学院,甘肃 兰州 730070;2.甘肃农业大学信息网络中心)
0 引言
灰狼优化算法[1(]grey wolf optimization,GWO)是Mirjalili 等人于2014 年提出的一种群体智能算法,通过模拟自然界中灰狼的领导层级和狩猎机制,采用搜索、包围和追捕攻击等群体行为,实现目标的优化,具有参数少、结构简单、易于实现等优点,该算法广泛应用于路径规划[2]、工程设计[3]、辅助医学图像分析[4]、广域电力系统稳定器[5]等方面。
虽然GWO 已经在工程和科学领域得到了广泛应用,但该算法仍存在一些缺点,如寻优精度低、缺乏多样性、探索和开发的不平衡以及在处理大规模问题中易过早收敛。针对以上问题,专家学者们提出了许多改进方法,如朱海波等[6]将差分进化与优胜劣汰混合策略加入算法中,提高了GWO 算法运算前期的探索能力和后期的开发能力。刘成汉等[7]为了提高算法的收敛精度,引入了改进的鲶鱼效应策略,以保证种群活力。王敏等[8]通过对当前群体中最优个体进行Rosenbrock 局部搜索,增强了GWO 算法的局部搜索能力并加快收敛速度。张悦等[9]利用自适应调整策略来控制参数调整和位置更新,提高了算法的收敛速度。Saremi 等[10]将动态进化种群(evolutionary population dynamics,EPD)算子引入GWO 算法,加快了算法收敛速度,增强了局部搜索能力。Zhu 等[11]将GWO 算法与差分进化算法结合,利用差分进化算法强大的搜索能力使GWO及时跳出停滞,提高了算法收敛速度。
基于以上分析,本文提出一种改进的灰狼优化算法(dynamic approach gray wolf optimizer,DAGWO)。首先,为灰狼个体增加直接跟随最优头狼攻击猎物的行为方式,从而增加其捕获猎物的机会,以提升算法的收敛速度和寻优精度。其次,提出基于停滞检测的随机初始化策略,以增加种群多样性,从而提高跳出局部最优的能力。
1 DAGWO算法
DAGWO 算法在每一次迭代中,群体中最优个体称为α狼,次优个体称为β狼,第三优个体称为δ狼,剩余个体称为ω狼。狩猎过程中,ω狼接受α、β、δ狼的领导向猎物位置靠近。狼群的捕猎行为分为跟踪、包围和攻击猎物三个阶段。灰狼群体逐渐接近并包围猎物的数学模型如公式⑴所示:
其中,t为当前迭代次数;为第t次迭代时猎物的位置;x(t+1)为第t+1 次迭代时灰狼的位置;A和C为系数向量。当|A|<1 时,狼群攻击猎物,当|A|>1 时,狼群寻找猎物。A和C的定义分别为:
其中,r1和r2为[0,1]之间的随机数,a称为收敛因子,其随迭代次数增加从2线性减小到0,即:
⑷式⑷中,tmax为最大迭代次数。狼群中其他灰狼个体根据α、β、δ狼的位置xα、xβ、xδ来更新各自的位置:
x(t+1)即为灰狼个体根据α、β、δ狼位置信息调整后的更新位置。迭代完成后,xα即为所求猎物位置。
2 新移动策略的DAGWO算法
在标准GWO 算法中,首先,由于ω狼在狩猎过程中向三只头狼(α、β、δ狼)所围成的区域移动,而不是向猎物最有可能的位置即α狼所在位置移动,因此并不能最快速的冲向猎物发起攻击,导致算法的收敛速度变慢。其次,在寻优后期,灰狼群体逐渐聚集于α、β、δ狼所确定的位置周围,有可能陷入小范围优化而导致算法无法求出目标函数的全局最优值。为解决上述问题,提出两种策略来改进GWO算法:
⑴提出一种新的ω狼位置移动策略,使得ω狼能够直接向猎物靠近。
⑵提出一种基于停滞检测的随机初始化策略,避免算法陷入局部最优。
2.1 ω狼位置新移动策略
DAGWO 算法中,增加ω狼直接跟随α狼,向猎物位置发起攻击或堵截的行为,以提高算法的收敛速度。改进策略的数学模型如下:
其中,r3,r4为[0,1]之间的随机数,F为控制搜索方向参数,随机取值为-1或1。xt为第t次迭代时ω狼的位置,为第t次迭代时α狼的位置,K 为卡方分布随机数,本文取值6。M 为一个控制系数,用来控制跟随α狼进行捕猎的ω狼数量,当M=0.2,表示有20%的ω狼会跟随α狼攻击猎物。x(t+1)为更新后的ω狼位置。式⑻中,当r4
灰狼个体与理论最优值的欧式距离(d)反映了整个种群与理论最优值的聚集程度。当d 较小时,表明整个种群聚集程度高,如果d迅速变小,则种群迅速聚集。本文采用GWO 和DAGWO 优化同一函数,记录迭代过程中d 的变化,图1 显示DAGWO 算法的迭代过程种群迅速聚集,而GWO 算法的迭代过程聚集过程缓慢,且d值远高于DAGWO 算法。因此,本文提出的ω狼位置移动策略能够显著提高算法的收敛速度。
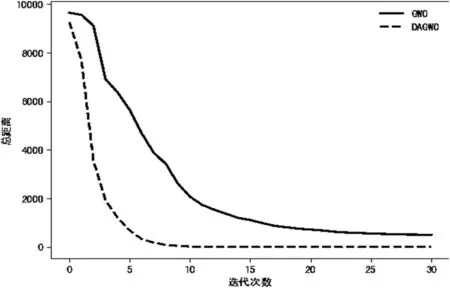
图1 种群聚集程度
2.2 基于停滞检测的随机初始化策略
标准GWO 算法寻优至中后期时,整个灰狼种群都趋向α、β、δ狼所在区域移动,一旦头狼陷入局部最优,就会使整个狼群陷入局部最优,从而导致算法出现停滞,无法探索更多区域。因此,需要对部分个体位置进行剧烈变动,寻找新的位置,带动整个种群跳出局部最优。本文提出一种基于停滞检测的随机初始化策略,在迭代过程中当适应度的变化率小于设定值时,则判定算法停滞,对种群个体进行随机初始化。其中,适应度变化率计算公式表示如下:
其中,fcur表示当前迭代次数的最优值,fbest表示当前迭代次数之前取得的全局最优值。rate表示最优值的变化程度,本文中取值10-5。当rate大于10-5则表明算法运行良好,不需要干预,反之当rate小于10-5时则表明算法停滞,需要对灰狼种群进行随机初始化。基于停滞检测的随机初始化策略伪代码如下:
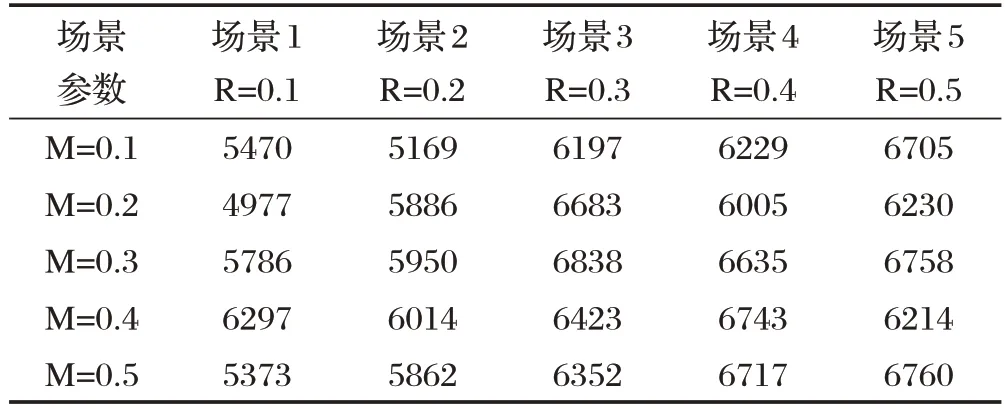
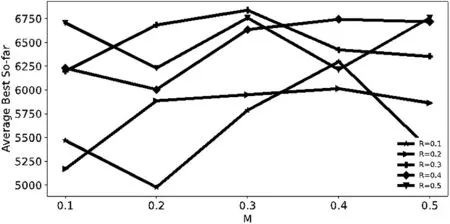
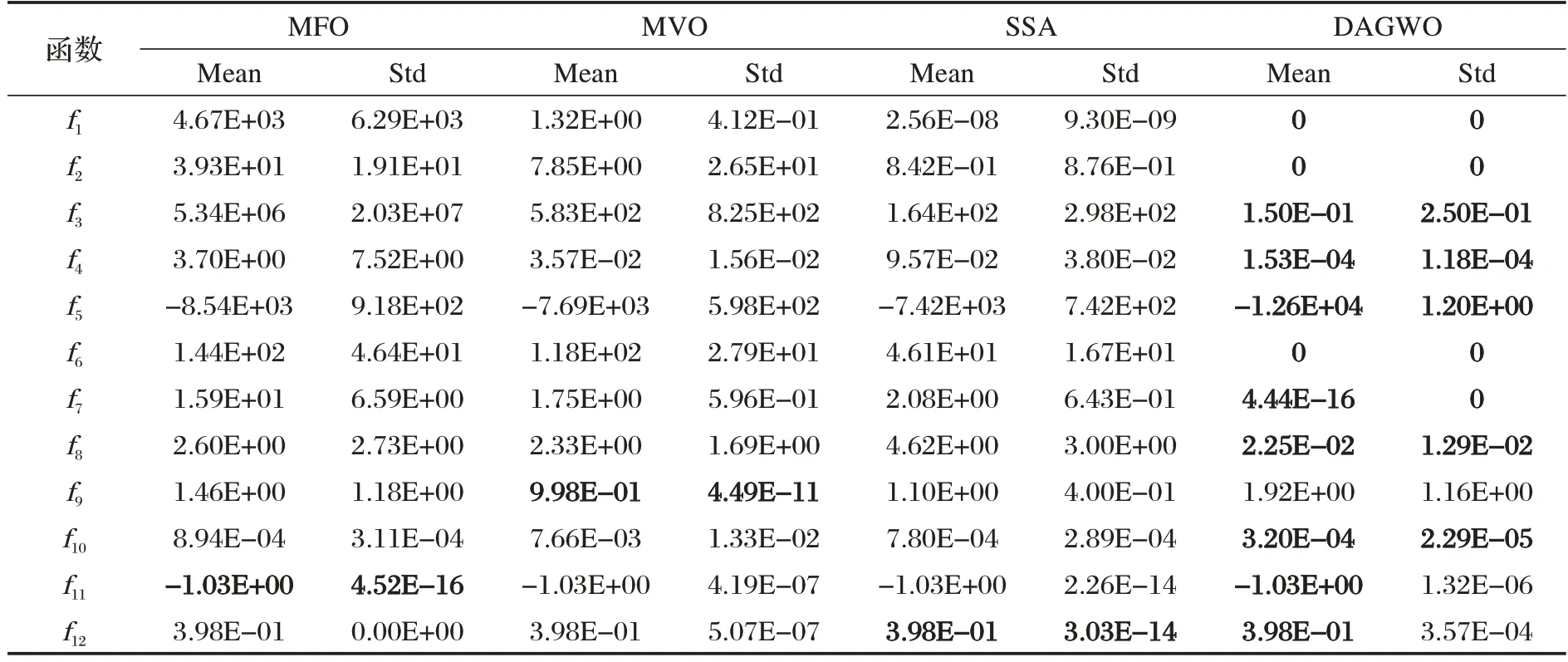
其中,r5、r6为[0,1]之间的随机数,a,b为搜索空间的下限和上限表示随机从灰狼中选择一个个体将其位置进行重新初始化。R 为控制系数,用来控制进行随机初始化的灰狼的概率。如果rate<10-5,则表明算法陷入了停滞需要采取增加多样性措施。ran是个随机数,当r5 DAGWO 算法的性能受到控制系数M 和R 的影响,需要谨慎选择这些参数。为了分析它们的影响并选择最佳组合,通过对CEC Composition Function 2(N=3)进行敏感性分析,在不同的M和R值组合下绘制了5 种场景,如表1 和图2 所示。结果表明,当M=0.2,R=0.1 时适应度值最佳。因此,DAGWO 算法的最佳控制系数为M=0.2,R=0.1。 表1 M和R参数敏感性分析 图2 参数M和R参数敏感性分析图 DAGWO算法执行步骤描述如下: 算法1:DAGWO算法 输入:种群大小N,最大迭代次数max 输出:最优位置xα 本文所有仿真实验均在CPU 为Inte(lR)Xeon(R)Gold 5118 CPU @ 2.30 GHz,内存为16GB 的主机上开发和执行。编程软件为Python 3.7。所有算法设置相同的种群数量和迭代次数,种群数量为30,迭代次数为500,搜索维度为30,以算法独立运行30 次的适应度值的平均值(Mean)、标准差(Std)作为评价指标,统计结果中的最优数据以加粗方式显示。 为了验证DAGWO 算法的有效性和优势,将DAGWO 算法与GWO 算法和其他参考文献中改进的灰狼算法:AGWO[12]、MGWO[13]、I-GWO[14],以及其他三种著名智能算法:飞蛾扑火算法[15(]moth flame optimization,MFO)、多元宇宙优化算法[16](multiverse optimizer,MVO)、樽海鞘群算法[17(]salp swarm algorithm,SSA)进行比较。选择与文献[18]相同的12 个基准函数测试算法的性能。测试函数如下:Sphere(f1)、Schwefel's problems 2.22(f2)、Generalized Rosenbrock's function(f3)、Quartic function with noise(f4)、Generalized Schwefel's problem 2.26(f5)、Generalized Rastrigin's function(f6)、Ackley's function(f7)、Generalized penalized function(f8)、Shekel's Foxholes function(f9)、Kowalik's function(f10)、Sixhump camel-back function(f11)、Branin function(f12)。其中f1-f4为多峰函数,f5-f8为多峰函数,f9-f12为为固定维度多峰函数。实验中各算法的参数设置如表2所示。 表2 算法参数设置 3.2.1 求解精度分析 在元启发式算法中,求解精度和收敛速度可以用单峰函数来衡量。因此,使用适应度值的平均值(mean)和标准偏差(std)来研究所提出算法的整体开发行为。表3 和表4 分别列出了DAGWO 与其他算法的测试结果。表3 中DAGWO 算法能在单峰测试函数f1、f2上找到最优适应度值,表明ω狼位置移动策略能够显著提升DAGWO的开发能力。在函数f4上DAGWO的性能仅次于I-GWO。表4中,对于函数f1-f4,DAGWO算法的平均值和标准偏差都优于其他三种算法。这些结果均表明ω狼位置移动策略可以有效提高DAGWO算法的求解精度和收敛速度。 表4 DAGWO算法与MFO、MVO、SSA算法测试结果对比 多峰函数(f5-f8)和固定维度多峰函数(f9-f12)具有多个局部最优解,会导致算法陷入局部最优。因此可用于评估算法的全局探索能力及跳出局部最优的能力。表3 和表4 所列实验结果表明DAGWO 算法在函数f5-f8上取得了有竞争力的结果。表3 表明DAGWO算法在函数f11-f12上取得了理论最优值。表4表明,对于固定维多峰函数f9-f12,DAGWO 算法在其中3 个函数上的寻优精度均优于其他算法。 基于上述实验结果,本文提出的DAGWO 算法采用的ω狼位置移动策略能够有效地提升算法开发能力,提高寻优精度;采用的基于停滞检测的随机初始化策略可以在一定程度上平衡算法开发和探索能力,在优化多峰函数时能够有效增强算法跳出局部最优的能力,帮助算法获得最优值。 3.2.2 收敛曲线分析 为了验证DAGWO 算法的收敛性能,以及跳出局部最优的能力,本实验列出了DAGWO 算法与其他智能算法基准测试函数迭代收敛曲线的对比图(图3)。限于篇幅限制,这里仅选取单峰函数f1、f3、f4,多峰函数f5、f7、f8,固定维度多峰函数f10、f11的收敛曲线对比图。由图3 可知,在单峰函数f1中,DAGWO 能够快速收敛到理论最优值且收敛速度大幅度领先,而其他算法均无法取得较好的收敛精度;在单峰函数f3、f4中,DAGWO 虽然未收敛到理论最优值,但在迭代前期收敛速度均快于其他算法;在多峰函数f5、f7中,DAGWO能够收敛到理论最优值且具有较快的收敛速度。在固定维度多峰函数f10、f11中可以看出,相比其他算法DAGWO 具有更强的全局搜索能力。在函数f11中,GWO、DAGWO均收敛到了最优值。 图3 算法收敛曲线对比 综上分析,DAGWO 算法在处理简单的单峰函数时,在收敛精度及收敛速度上优势明显,具有更优的收敛精度;在处理多峰函数时也能够跳出局部最优,获得较好的收敛精度。 为验证DAGWO 算法的实用性,通过经典的工程应用优化案例-减速器优化设计问题,对DAGWO 算法进行测试。设置算法的种群数量为50,迭代次数为1000,以算法独立运行30 次的最佳结果(包括最优值和最优设计变量)与人工峰群算法[19(]Artificial bee colony algorithm,ABC)、花斑鬣狗算法[20](Spotted hyena optimizer,SHO)、MGWO[21]算法、RW-GWO[22]算法、WF-GWO[23]算法、GWO 算法进行比较。为确保数据的准确性,相关算法数据均来自于原文献。 DAGWO算法的应用之一是减速器优化设计问题。减速器优化设计问题的目标是使减速器的体积(或重量)最小,其设计结构如图4[24]所示,该问题包含7 个设计变量和11 个约束条件,其中设计变量分别为:端面宽度x1、齿模x2、小齿轮齿数x3、第一轴长度x4、第二轴长度x5、第一轴的直径x6、第二轴的直径x7。其数学模型如下: 图4 减速器结构设计图 表5列出了不同算法求解减速器优化设计问题的最优解。从表5 可知,在减速器优化寻优结果中,DAGWO 获得了最佳解决方案,且优势较为明显。这表明其在用于解决实际工程问题时具有较好的寻优能力及实用性。 表5 不同算法求解减速器优化设计的最优解对比 针对标准GWO 算法收敛速度慢、容易陷入局部最优问题,本文提出了一种新的基于移动策略的灰狼优化算法。新的ω狼位置移动策略增加了狼群攻击的多样性和随机性,提高了算法的收敛速度和寻优精度。同时,基于停滞检测的随机初始化策略增加了种群多样性,提高了算法的全局搜索能力,避免陷入局部最优。仿真实验结果表明,DAGWO 算法两种改进策略可以有效提高收敛速度和求解精度。减速器优化设计工程实例的结果验证了DAGWO 算法在解决工程优化设计问题时的适用性。未来的研究将聚焦于DAGWO算法在更多实际优化问题上的应用。2.3 参数敏感性
2.4 DAGWO算法步骤
3 仿真实验与分析
3.1 实验环境及参数设置
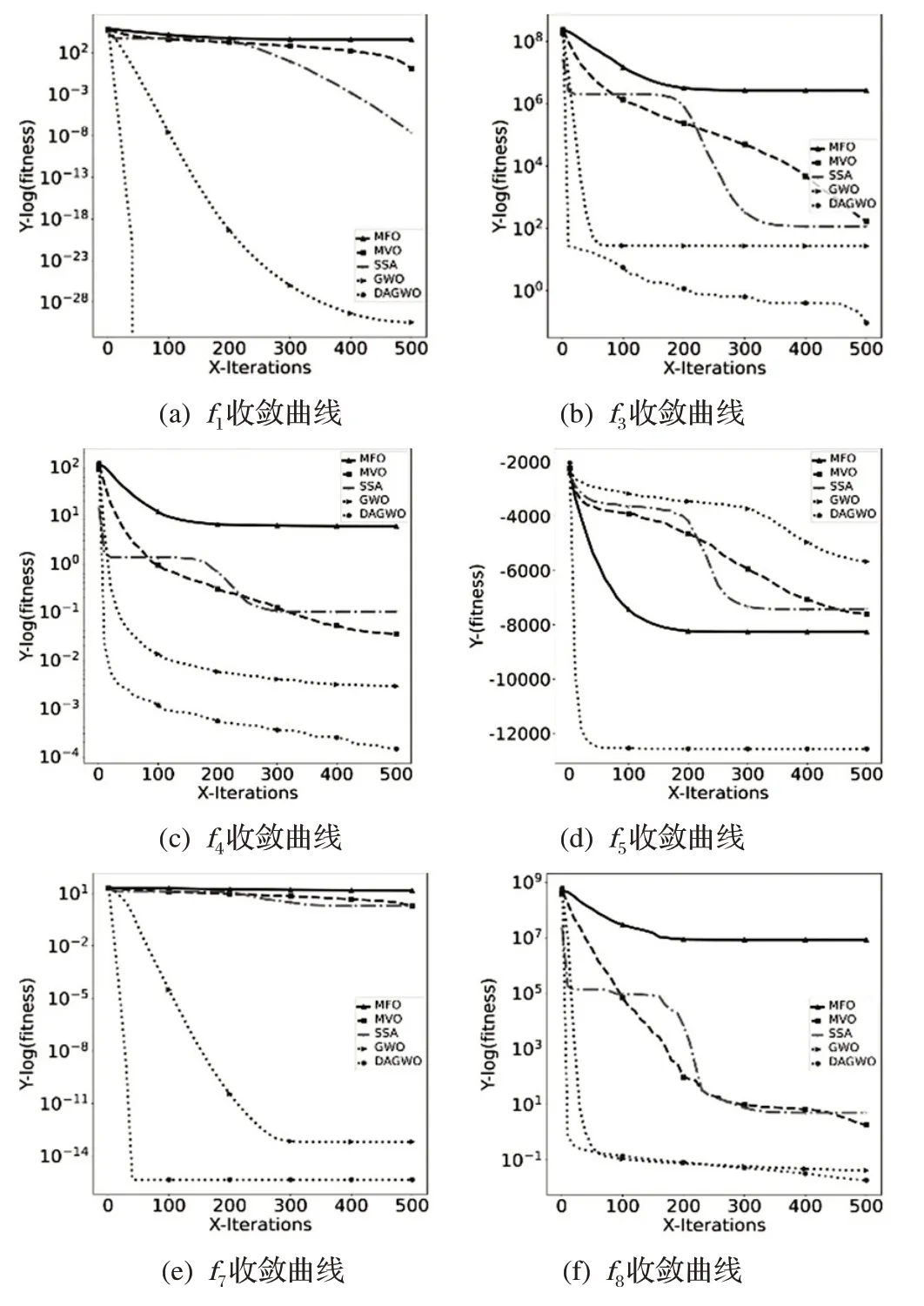
3.2 基准测试函数仿真实验

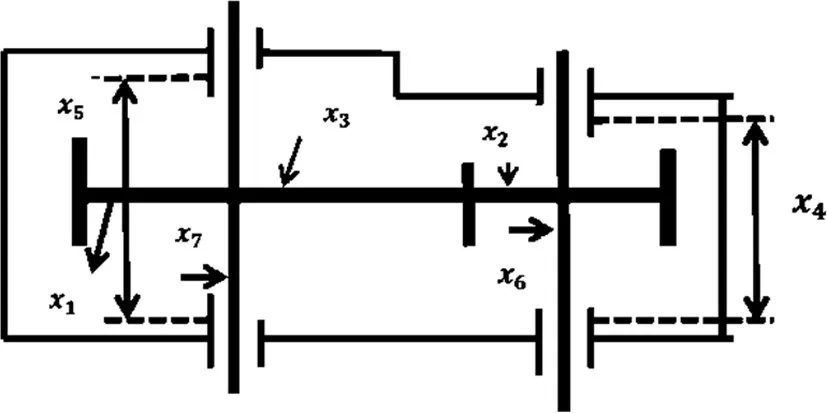
4 工程应用及结果分析
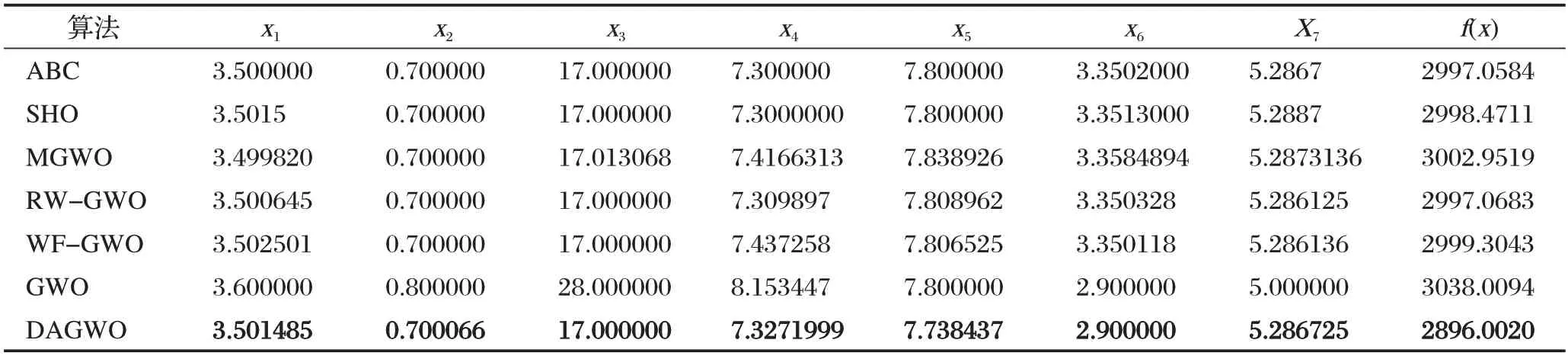
5 结束语

