基于遗传算法的无人机农药喷洒航迹规划

赵 越， 李言锋

（上海理工大学管理学院， 上海 200093）

0 引 言

近年来，无人机在农业领域的应用日益广泛，植保无人机凭借其灵活性，可以在农田中进行植物检测、施肥、喷洒农药等操作。 中国农业土地辽阔且分布不均，不仅有集中的大块田地、也有较为分散的小块农田，不只有单一作物种植、也存在种植作物分散的多样化种植区［1］，因此对多区域无人机航迹规划进行研究具有实际应用价值，可以减少不必要的航行和能耗，降低任务成本。

针对单架无人机的路径规划问题，已经得到了广泛的研究和探讨。 武锦龙［2］和李靖等学者［3］在避开障碍物的同时对多区域喷洒路径进行全局规划。 当单架次无人机对多区域执行遍历任务时，王嘉琪［4］和Liu 等学者［5］分别使用改进编码的差分进化算法和基于蚁群二元迭代优化的动态遗传算法对转化后的TSP 问题进行求解。 也有路径规划研究以多目标来确定任务收益，如飞行总路程、多任务区的侦查时间［6］、目标摧毁概率［7］等。 当无人机被分配到一个区域执行任务时，提出了全区域覆盖搜索路径规划问题［8-9］，大多数研究方法基于无人机飞行航向对无人机工作区间进行划分与路径规划。 多架无人机的路径规划也得到了研究。 杜芳芳等学者［10］等和张哲等学者［11］研究了多无人机以最小成本完成任务目标的MTSP 问题，并泛化出异构无人机执行不同任务的多车型VRP 问题［12］等。

上述研究方法大多是将区域看作一点，将路径规划问题转化为旅行商问题或多车辆路径问题，或者对单一区域内的路径覆盖问题展开研究，但在农业应用中，将区域转化为一点并不实际，无人机在区域内的覆盖路径将直接影响区域间的飞行距离。 针对上述问题，本文从超级网络的角度，对多作业地块之间的调度问题以及地块内覆盖路径选择问题进行描述，建立更具一般化的数学模型，并设计出一套高效求解的算法，再与将区域转化为一点的处理方法做结果对比，证明本方法的可行性。

1 问题描述

假设现有若干不连续地块，使用无人机对其执行喷洒任务，使得路径从出发点开始遍历所有地块并回到出发点后无人机能耗成本最小。 将地块间的飞行任务看作旅行商问题，将地块内的飞行任务看作覆盖路径规划问题，因此，无人机执行地块喷洒任务为旅行商问题与覆盖路径规划问题的结合。

机械覆盖路径方式主要有牛耕往复法和内外螺旋法，在相同大小地块内作业时，内外螺旋法的飞行长度大于牛耕往复法，因此本文选择牛耕往复法作为区域内无人机作业方式。 牛耕往复法在矩形区域作业方式有2 种，如图1 所示。 图1 中，a、b为地块的长度与宽度，d为无人机作业直径，图1 （a）、（b）两种方式的作业长度相同，均为但由于转弯会产生一定的非作业长度，将其称为“转弯长度”，分别为可以看出（b）方式的转弯长度更小，因此在区域内使用（b）方式遍历路径可使飞行能耗更小。 但是如果只追求区域内路径长度最小，可能会导致区域间飞行长度或转弯角度增加，考虑到地块的飞入点与飞出点会直接影响区域间的飞行路径，因此要获得最优的多区域覆盖路径，应合理选择地块飞入点，使得整体飞行能耗最小。

图1 无人机覆盖路径方式示意图Fig. 1 UAV coverage path planning diagram

使用牛耕往复法对区域内进行遍历，一个地块内有8 个可行的飞入点，假设区域长度与宽度均为作业直径的整数倍，那么8 个飞入点对应8 个可行的飞出点，将其进行编号，如图2 所示。

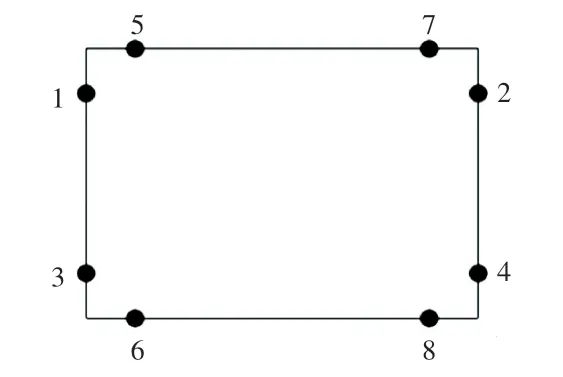
图2 区域进入点示意图Fig. 2 Regional gateway diagram

超级网络是指通过添加虚拟节点和弧段形成一个网络拓扑结构，对研究对象的行为与特征进行抽象化描述的一种研究方法［13］。 在地块规模较大时，利用超级网络的虚拟节点与虚拟弧段代替无人机真实飞行路径，使得问题与数据信息更加简洁清晰。下面利用超级网络对无人机喷洒农药过程进行描述，如图3 所示。 地块飞入的8 个点对应了8 条不同的覆盖路径，将无人机在地块内的8 条覆盖路径转化为8 条虚拟弧段，该虚拟弧段包含区域内飞行距离、覆盖线路起点坐标、终点坐标等已知信息。 地块间的飞行路径实际为地块内覆盖线路终点至下一地块覆盖线路起点的弧段，由于无人机实际以哪一条线路覆盖地块未知，因此将地块看作一矩形点用虚拟弧段将其连接起来，该矩形点包含地块排列序号与覆盖线路序号的未知信息，该虚拟弧段包含地块间飞行距离的未知信息。

图3 超级网络示意图Fig. 3 Super network diagram

2 无人机航迹规划模型

考虑研究问题的情景，对模型建立进行了如下假设：

（1）无人机在飞行时通过改变飞行方向和姿态来完成转弯和变向操作，而不需要绕着一个固定的曲率半径进行圆弧形的转弯，即飞行轨迹为直线或折线；

（2）实施喷洒任务的地块为矩形区域且不重叠；

（3）起点看作边界点坐标和飞入飞出点坐标均为（0，0）、区域内各线路距离均为0 的地块；

（4）无人机有足够的动力完成该任务，并以恒定的高度飞行。目标函数为：

约束条件为：

模型中有2 类符号：模型参数和决策变量。 在式（1）～式（6）中，模型参数主要有：n为目标点总数，包括1 个出发点和n- 1 个地块；为无人机在覆盖地块i的路线起点，共8 条线路；是无人机在覆盖地块i的路线终点，共8 条线路；为无人机以第k条路线覆盖地块i的终点与无人机以第l条路线覆盖地块j的起点的欧式距离；为无人机以第k条线路覆盖地块i时的飞行距离。 决策变量主要有：xij表示无人机是否将从地块i移动到地块j，如果是，xij＝1，否则xij＝0；表示如果无人机以第k条路线覆盖地块i，则＝1，否则＝0；zjl为如果无人机以第l条路线覆盖地块j，则＝1，否则＝0。

具体来说，式（1）的目标函数为最小化飞行距离；式（2）、式（3）表示每个地块只能进入一次；式（4）、式（5）表示每个地块只能以一种线路覆盖；式（6）的约束表示消除子环路、但不消除最大的环路。

3 模型求解

遗传算法是一种启发式优化算法，通过模拟自然界中的进化过程来解决问题。 将问题的解表示为某个个体的基因型，通过选择、交叉和变异等基因操作，产生新的解，并逐步优化当前的最优解。 现已广泛应用于优化问题、机器学习、图像处理等领域。

3.1 编码

本文采用顺序表示的编码方式，每一个数字代表一个地块，遍历所有的地块产生一条染色体、即产生了1 个解，以6 个地块1 个起点为例，地块编码是2～7 的数字，若生成的染色体是1342756，表示从起点1，依次经过地块3、4、2、7、5、6，最终回到起点1的一条路径回路。

3.2 适应度求解

假设由n个地块构成的染色体为｜C1｜C2｜…｜Cn-1｜Cn ｜，个体的适应度值为f＝-F，其中F为从起点出发遍历所有地块回到起点所产生的距离与地块内作业距离的总和。 适应度越大表示染色体越优，反之越劣。 定义了一个计算目标函数值F的函数CalObj，输入参数为区域信息（包含地块编号、地块内线路编号、地块内遍历长度）以及出发点坐标，将地块内线路编号序列映射到实际的路径上，如Xnow＝｛2，4，6，3，2，8｝，假设最大地块数为6，那么进行6 次for 循环，将Xnow的第一个元素对应的区域的信息存储在一个新的矩阵中，其中新矩阵已包含起点坐标，从Xnow数组中删除第一个元素，变为5 个元素，再进行下一次循环，根据新生成矩阵中节点之间的距离计算目标函数值F。

3.3 交叉与变异

交叉操作采用“子路径互换交叉”的交叉方法，确定待交叉的2 个父代个体，从变量列数中随机生成2 个位置，确定需要进行交叉的位置区间，即2 个随机位置之间的所有位置。 将父代1 中位置区间的值与父代2 中相同的值进行交换，将父代2 中的位置区间的值与父代1 中相同的值进行交换。 变异操作采用的是2-opt 组合优化邻域算子，是一种基于交换2 个城市路径中间的路径段来产生新解的变异方法。 从待变异的个体中随机选择2 个位置，将这2 个位置之间的路径段反转，即路径上这2 个地块之间的所有地块的顺序反转，得到一个新的路径。

3.4 变邻域深度搜索

变邻域深度搜索实现了5 种不同类型的邻域操作，包括交换邻域（swap）、插入邻域（insert）、2-opt邻域、or-opt 邻域和反转加上插入邻域。 对于每种邻域操作，该函数都会在当前解的邻域中进行搜索，生成一个新解，并计算新解的目标函数值。 如果新解的目标函数值比当前最优解更优，则更新最优解，并记录产生最优解的邻域操作的具体参数，即交换、插入、反转等操作的具体位置。

3.5 基本步骤

步骤1种群初始化。 根据地块顺序对该问题进行编码形成初始化种群。

步骤2适应度求解与选择。 根据染色体基因的排列得到初始解的目标函数值，并计算种群中每个染色体的适应度以及种群中最佳的适应度，同时使用锦标赛选择法对随机选取的2 个个体进行比较，选取适应度值最优的个体作为本次选择的结果。

步骤3染色体交叉操作。 首先通过锦标赛从当前种群中选择出一组父代个体，然后通过交叉概率来决定是否进行交叉操作。 如果需要进行交叉操作，将这2 个父代个体进行子路径互换交叉，生成新的子代。

步骤4染色体变异操作。 由交叉操作生成的染色体通过变异概率来决定是否进行变异操作，使用2-opt 交换方法进行变异，从而得到一个新的基因序列。

步骤5局部搜索操作。 将交叉变异后的子代个体作为下一代种群并进行局部搜索操作，得到更新后的解。

重复步骤2～5，直至满足终止条件，即可输出当前的迭代次数和无人机地块访问顺序。

4 仿真实验

实验在Matlab R2022a 环境下构建基于遗传算法的植保无人机路径规划模型。 本文实验地块数据来源于某种植区地图信息。 首先选用6 块区域，区域A、B、C、D、E、F的边界点坐标与中点坐标见表1，无人机喷洒直径为5 m。

表1 各地块边界点坐标与中点坐标Tab. 1 Coordinates of boundary points and midpoints of each block

首先使用将区域转化为地块中点的方法对该案例进行求解，设交叉率crossover_prob＝0.6，变异率mutation_prob＝0.2，种群大小pop＝50，当进化到第3 代时得到最优路径为A-C-B-D-F-E，确定了地块顺序后，使用Matlab 内置遗传算法求得地块内线路序号为6-5-4-2-7-2，得到距离最优值为1 065.4 m。

如果考虑地块内飞行路线对区域间飞行距离的影响对该案例进行求解，设交叉率crossover_prob＝0.6，变异率mutation_prob＝0.2，种群大小pop＝50，迭代50 次，进行10 次实验，记录每次实验下的区域顺序、线路序号、距离最优值等结果，并得到最大值、最小值和方差，见表2、表3。

表2 迭代50 次实验结果Tab. 2 The experimental results after 50 iterations

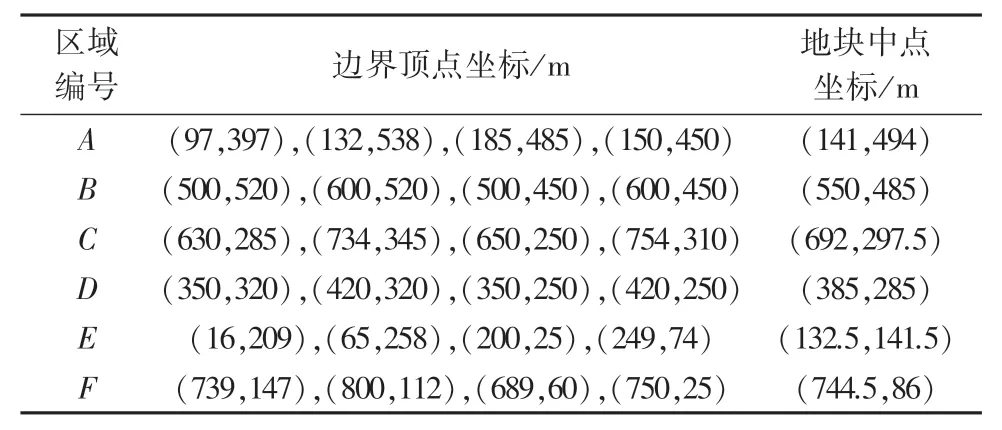
表3 各地块边界点坐标与中点坐标Tab. 3 Coordinates of boundary points and midpoints of each block

根据实验结果可看到， 当区域顺序为A-B-D-F-C-E，对应线路序号为6-6-1-7-2-2 时，飞行距离最小值为935.15 m，与将区域转化为地块中点相比飞行距离减少12.2%。 达到飞行距离最小值的次数为4 次，方差较小，结果更加稳定。 迭代50 次进化过程如图4 所示，对模型进行50 代循环求解时，可以看出算法收敛较快，下降趋势明显，第8 代求得疑似最优解。 航迹规划示意如图5 所示。图5 中，蓝色线为无人机在区域内作业路径，红色线为区域间飞行路径，绿色点表示地块飞入点，黄色点表示地块飞出点，箭头为飞行方向。

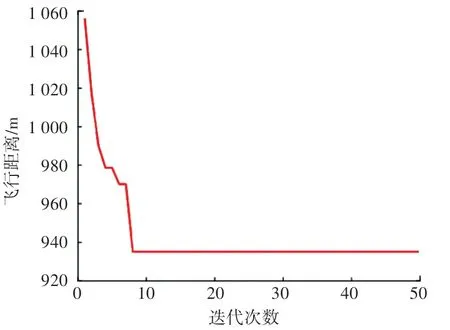
图4 迭代50 次进化过程图Fig. 4 The evolutionary process diagram for 50 iterations

图5 航迹规划示意图Fig. 5 Schematic diagram of path planning

当地块距离较远时，同样选取6 块区域进行求解，区域A、B、C、D、E、F的边界点坐标与中点坐标见表3。

若使用将区域转化为地块中点的方法对该案例进行求解，当进化到第3 代时得到最优路径为A-B-C-F-D-E，确定了地块顺序后，使用Matlab内置遗传算法求得地块内线路序号为5-2-2-7-8-8，得到距离最小值为10 291 m。 若考虑地块内飞行路线对区域间飞行距离的影响对该案例进行求解，进行10 次实验，当区域顺序为E-A-D-B-C-F，对应线路序号为5-6-5-6-1-1 时，得到飞行距离最小值为9 673.6 m，与将区域转化为地块中点相比飞行距离减少6.0%，因此当地块距离相距较近时，地块飞入飞出点对区域间飞行距离的影响更大。

为了验证该方法在解决更大规模问题的能力，创建了20 个矩形区域。 进行100 代循环求解，种群大小为200，记录10 次实验下的区域顺序、线路序号、距离最优值、最小值和方差等结果，见表4。

表4 迭代100 次实验结果Tab. 4 The experimental results after 100 iterations

根据实验结果可知，当区域顺序为7-16-20-13-18-1-4-2-14-5-3-17-15-6-8-10-12-9-11-19，对应线路序号为7-7-3-8-4-6-5-4-2-5-3-8-1-1-2-1-7-2-2-4 时，飞行距离最小值为3 331.49 m。飞行航迹规划示意图如图6 所示（地块内飞行线路省略）。 对模型进行100 代循环求解时，可以看出算法收敛较快，下降趋势明显，第50 代求得疑似最优解，如图7 所示。

图6 较大规模的区域航迹规划示意图Fig. 6 Large-scale area trajectory planning diagram

图7 迭代100 次进化过程图Fig. 7 The evolutionary process diagram for 100 iterations

5 结束语

本文针对无人机农药喷洒问题，考虑了地块飞入飞出点对总飞行距离的影响，建立了一般化的区域间覆盖路径规划模型，将无人机多地块农药喷洒问题转化为旅行商问题与覆盖路径规划问题的结合。 使用遗传算法对2 种区域规模的算例进行求解，验证了该方法的可行性，得到了最佳迭代次数下最优飞行距离。 未来将对不规则地块进行覆盖路径规划研究。