基于不同覆土厚度的地铁车站无梁结构体系受力性能研究

李玉洁

（中铁上海设计院集团有限公司,上海 200070）

0 引言

近年来，我国轨道交通的发展势头十分迅猛，对于地铁车站来说，采用无梁结构体系不仅能解决为满足净空要求带来的工程造价增加的问题，还能便于管线铺设，使管线的铺设更加灵活[1]。同时，无梁结构顶板的平整和整体性较好，顶板防水效果得到显著提升。因此，对于地铁车站无梁结构体系的受力性能研究具有十分重要的意义。

该文以苏州某标准单柱双跨岛式车站为研究背景，运用Midas Gen 软件对该车站在不同覆土厚度下顶板的受力性能展开对比分析，提出了无梁结构体系的相关设计要点。

1 工程概况及模型方案

1.1 工程概况

苏州轨道交通3 号线某车站为地下两层单柱双跨岛式车站，车站主体结构外包总长198.2 m，标准段宽19.7 m。车站中柱尺寸0.8 m×1.1 m，柱距9 m，围护结构采用800 mm 厚地下连续墙，车站标准段断面图如图1 所示。

图1 车站标准段断面图

1.2 模型方案

（1）模型对比方案。运用Midas Gen 软件建立地铁车站基本三维模型，为节省软件运算时间，对车站主体结构取半建立基本三维模型，如图2 所示。

图2 车站基本三维模型图

在基本三维模型基础上建立6 组对比分析模型，分析模型如表1 所示。

表1 分析模型

（2）单元选取。模型中顶、中、底板及侧墙均采用板单元进行模拟，混凝土强度等级为C35；梁、柱采用梁单元模拟，混凝土强度等级为C35、C45。梁、板单元网格划分长度为0.5 m（研究区域细化后为0.2 m），满足数值模拟精度和工程需求。

（3）边界条件及荷载施加[2-3]。对于结构底板，用弹性支撑来模拟土体作用，选择面弹性支撑转换为弹性连接，输入底板所在土层的基床系数，弹性连接长度为1 m。

该车站围护结构采用地连墙，与内部结构侧墙组成复合墙结构形式，在永久使用阶段围护结构承受外侧土压力作用，内部结构侧墙仅承受水压力。顶板恒载按γh计算（γ为覆土容重，一般取18.5 kN/m3，h为覆土厚度），地面超载取20 kPa；中板恒载取5 kPa，活载取8 kPa，底板水浮力作用及侧墙水土压力作用均根据相应覆土厚度确定。

2 主要计算结果分析

选取顶板一边格板（如图3 矩形框所示），沿x轴和y轴按1 m 划分为9 个板格条带，以所选板格左上角角点为坐标原点（0,0）建立坐标系(上边缘为墙边，下边缘为柱边)，得到x轴与y轴方向的内力分布。

图3 板带选取示意图

分析模型A 所选的板格主受力方向Myy云图如图4所示。

现对模型A 及其余各模型计算结果中取x=1、x=5、x=8 的同区域板带，提取相应计算分析数值后，分别绘制Myy内力（主受力方向）对比曲线，如图5 所示。

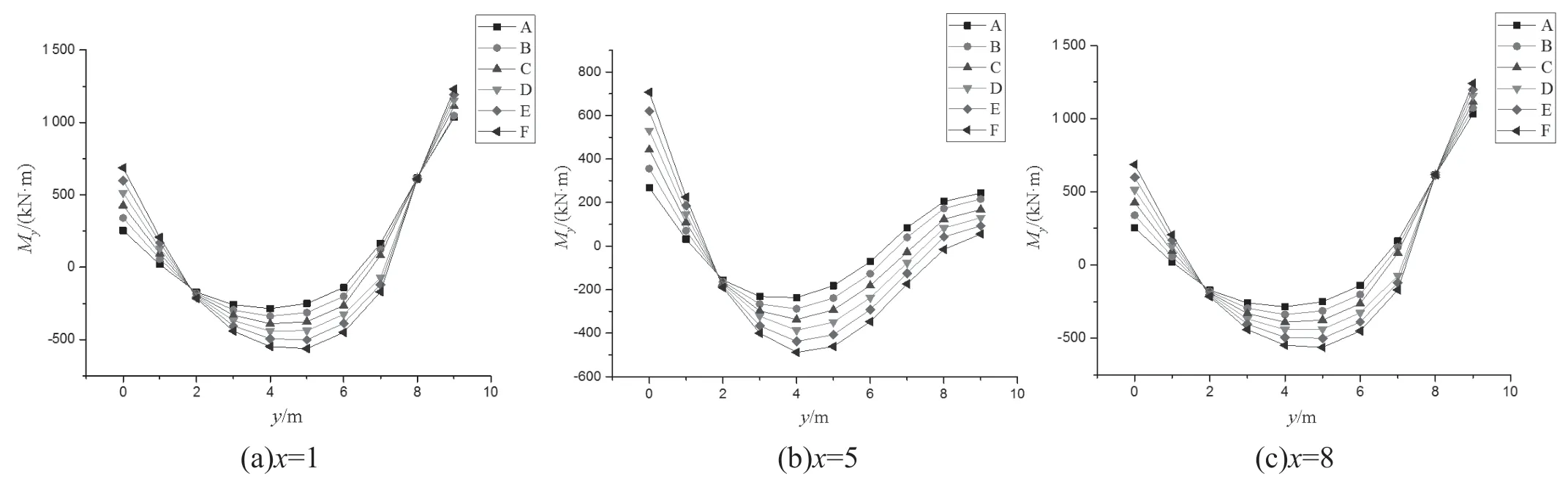
图5 相同板带区域Myy 变化曲线

不同覆土厚度下各模型的双向弯矩、剪力最值如表2 所示，正负弯矩板带宽度如表3 所示。

表2 不同覆土厚度下内力最值

表3 不同覆土厚度下正负弯矩板带宽度

根据各模型弯矩云图、变化曲线以及表2~3 分析可知：

（1）随着覆土的增加，各模型板带Myy内力变化规律一致，基本呈线性增长趋势，且最大正负弯矩位置与常规地铁车站梁柱结构体系一致，同时得出以下规律：

①y=1~6 时，Myy变化规律一致，Myy内力与梁柱体系下内力基本一致，由于内力重分配的作用，局部内力会小于梁柱体系下内力，此范围内配筋按照梁柱体系下最大正负弯矩指导Myy配筋；

②y=7~9 时，即柱支座影响范围内，Myy均大于梁柱体系下弯矩值，该范围需根据实际弯矩值进行针对性设计。

（2）由表2 可知，随着覆土的变化，最大剪力值为呈线性增加的趋势，线性关系近似为Vmax=600H+2100（H为覆土厚度/m）。经验算，当覆土厚度为大于1.5 m 时，剪力值大于3 090 kN，不满足顶板厚800 mm 的抗剪承载力要求，因此，应考虑增加板厚、增设柱帽等方式。

（3）由表3 可知，随着覆土的增大，受拉板带宽度不发生变化，表明覆土厚度变化对Myy的各支座范围内板带宽度的影响不大。在覆土厚为1.5~4 m 时，墙边上侧受拉板带宽度可取1.4 m，跨中下侧受拉板带宽度可取5.5 m，柱范围内上侧受拉板带宽度可取2.1 m。

3 框柱影响半径及柱帽范围

3.1 框柱影响半径

由于覆土厚度的增加对弯矩值和剪力值的变化基本呈线性增加，因此，当顶板在柱附近处的弯矩等于墙边支座弯矩时定义柱在x轴方向的影响半径Rx。

根据《地铁设计规范》[4]规定车站结构构件裂缝限值为0.3 mm，分布钢筋的配筋率不宜低于0.2%。通过计算，根据Mxx方向的弯矩，可定义当柱范围顶板（板厚800 mm 情况下）的弯矩为300 kN·m 为柱在y 轴方向的影响半径Ry。不同覆土厚度下Rx、Ry值见表4 所示。

表4 不同覆土厚度下Rx、Ry 值

由表2、表4 可得以下规律：

（1）覆土厚度增加时，作用在顶板上的荷载增加，柱范围内与墙边支座作用一致的位置变形增加，支座作用得到削弱，使得与墙边支座作用相同的位置继续往柱边靠近，Rx从3.6 m 线性减小至1.4 m，影响半径呈减小趋势。

（2）覆土厚度的增加会使得墙、柱支座作用相对削弱，从而降低原位置处支座负弯矩，框柱一定范围内Mxx增加幅度明显大于Myy，综合支座效应和弯矩增加幅度，导致Ry数值基本无变化，均为2.6 m。

根据以上数据及分析可以得出，随着覆土的变化，框柱横向的影响无变化，框柱纵向的影响范围拟合公式近似为Rx=3.4-0.5H（H为覆土厚，2.0 m ≤H≤4.0 m）。

3.2 柱帽设置

在顶板厚度受弯和抗剪计算不满足要求时，顶板需要加厚，加厚区域即为柱帽设置区域。分别定义柱帽横向长度为Dx（柱帽宽度的一半）与纵向长度Dy（柱帽长度的一半）。通过对计算结果的提取，得出不同覆土厚度下的Dx和Dy的最大包络值，并绘制Dx和Dy变化曲线，如表5 和图6 所示。

表5 不同覆土厚度下Dx、Dy 值

图6 Dx 和Dy 变化关系曲线

通过表5 和图6 可知，Dx与Dy基本呈线性增加，表明覆土的变化对柱边板带弯矩有一定的影响，在覆土为1.5~4.0 m 时，对Dx与Dy可用线性公式进行拟合，可得出Dx=0.2+0.1H，Dy=0.2+0.1H（其中H为覆土厚，单位均为m）。

4 结论

该文通过对某地铁车站在不同覆土厚度情况下运用Midas Gen 进行有限元分析，得出以下几个主要结论：

（1）在不同覆土条件下，各分析模型内力变化规律相同，无明显突变点，最大正负弯矩、最大剪力均呈线性变化[5]。

（2）通过对各模型的内力分析，得到各模型正负弯矩板带宽度，实际工程中可以此来对该区域进行合理加强配筋。

（3）对于一般地铁车站覆土大于1.5 m，板厚为800 mm 的情况下，均需设置柱帽来满足顶板抗冲切要求。

（4）通过对柱帽尺寸的包络设计，得出柱帽范围的一般性规律，类似工程中可以参考以确定增设柱帽的范围，并对柱帽合理设计，来满足顶板抗冲切要求。

（5）该文对常规地铁车站顶板板厚为800 mm 情况下，进行不同覆土情况下的受力分析，得出了一般性结论，后续研究和工程应用中应考虑对柱跨、板厚等情况进行进一步分析，以确定更为合理的地铁车站无梁结构设计方案。