网络学习空间中学习画像的标签模型构建研究

赵 春,李 欣

(成都锦城学院 计算机与软件学院,四川 成都 611731)

1 概 述

在“互联网+教育”的背景下,随着移动智能设备的普及和数字化学习资源的极大丰富,网络学习逐渐成为一种主流的学习模式。学生在网络学习空间中的学习行为产生了大量的学习数据。利用基于大数据的用户画像技术对学生的线上学习数据进行挖掘分析、构建学生学习画像变得现实可行。

用户画像是根据用户数据提炼出的描述用户属性及行为的标签集合[1],被广泛地应用于描述用户特征、用户兴趣和用户偏好等[2-4]。学生画像则是用户画像技术在教育领域的应用,反映了学生的学习特征和学习行为。它可以帮助教师理解教学实施情况,也可以辅助制定新的教学策略[5]。余明华等将学生画像划分为能力属性、行为属性和兴趣属性,以数据分析和人工手段相结合的方式建立了学生画像的标签体系[6]。杨长春等认为创建用户画像的过程就是依据构建的用户模型在用户信息中得到特征,并将特征标签化的过程[7]。他从学生的基本特征、学习特征、学习能力、素质与偏好五个维度进行了学生画像建模。黄文林认为学生画像是用能够反映学生的特征描述、行为诊断和需求预测属性的三类标签来刻画,并进行可视化呈现的用户画像方法[8]。任红杰认为学生画像是根据学生的基础信息、学习习惯、学习偏好、学习行为和学习期待等方面的数据信息构建出来的标签化学生模型[9]。杨彩霖认为可以从线上学习的活跃度、参与度、持久度、学习效果和学习预警五个维度刻画学生个体画像,并对每个维度赋予相应的权值[10]。

以上研究基于各自不同的数据基础和画像需求,从不同的角度提出了构建学生画像标签模型的方法。它们各自抽取的数据维度和粒度虽然有所不同,但学习能力和学习行为均被包含其中,是最被研究者重视的两个维度。上述研究中提到的学习习惯和学习偏好等维度完全可以合入学习行为维度中体现。学习能力标签模型可以以学生的学习成绩为主要依据进行分析刻画,而学习行为标签模型的构建所依赖的数据维度则相对较为复杂,比如设备使用习惯、登录时间习惯、作业完成习惯和学习响应习惯等。

在构造学习画像标签的过程中,传统方式采用的单纯统计类标签维度刻画的模式具有颗粒度粗糙、标签等级不够精准的缺陷。因此很多研究者利用聚类方法进行用户分类与画像构建。张毅认为大数据背景下用户画像的统计方法可以简单概括为针对用户属性加以统计,建议从统计分析视角出发,明确画像指标,做好主客观指标之间的转换,从而获得用户画像更详细的特征[11]。翟鸣宇等为适应教育大数据中含有的大量类别信息,采用了K-prototype聚类方法对高校学生大数据进行聚类,以此构建学生画像[12]。许智宏等通过改进K-means算法和PCA算法来对学生行为进行用户画像[13]。凌玉龙等在引入马氏距离的基础上通过改变初始聚类中心的选择来改进K-means算法,从而适应学生群体聚类场景,更好地刻画学生的消费画像[14]。王惠惠等在实施学生群体画像的过程中为了提高聚类结果的精确性和鲁棒性,利用KMeans、KModes和GMM三种聚类方法构建基聚类器,并通过投票方法对聚类结果进行集成处理[15]。袁苗苗等基于改进的K-means聚类算法针对记录数据和用户评论数据分别建立了用户兴趣特征标签库和用户消费特征标签库,提出了多数据源融合的用户画像构建方法[16]。

由此可见,K-Means聚类算法成为研究者构建用户画像时最常被采用的方法,但是KMeans等聚类算法鲁棒性不好,对噪声敏感,同时存在对离散型特征无法进行有效训练的缺陷。考虑到不同维度的特点,针对具有代表性的学习能力及学习行为标签,文中通过提出一种新的调整的线性加权变异系数算法,实现了学生学习能力标签模型;同时基于偏好随机变量概率分布理论,利用箱线图和k百分位数方法构建了学生行为标签模型,较好地实现了学生画像的精准构建。

2 学习能力标签模型

文中使用的学生学习数据集按照教学周阶段性产生、采集,具有连续的数值型特征,同时也具备周期性、动态性的特点。对学习能力的阶段性刻画,集中趋势度指标是一种常用的方法,如均值、众数、中位数等,因为这些指标代表了学生的平均水平。但是均值的鲁棒性非常差,容易受到噪声的影响,而众数则更加适合离散的数据特征。中位数虽然克服了上述两种指标度量的缺点,兼具鲁棒性和数值特征适应性,但是又没有考虑到每一次成绩的变化波动情况。离中趋势度指标是另外一种可以用于刻画学习能力的方法。但是如果单纯使用方差或者标准差,虽然能够度量数据的离散程度,但是忽略了成绩数据的周期动态性特点,即每周都会有新的成绩数据产生。成绩数据集合以周为单位进行扩充,样本容量每周发生变化。因此采用变异系数(Coefficient of Variation,CV)的形式度量学习能力稳定性是较为合适的方法。CV没有量纲,不受样本容量限制,这样就可以对学习能力稳定性进行客观比较。

传统的变异系数CV的计算方式为原始数据标准差与原始数据平均数的比,如式(1)所示:

(1)

传统的变异系数CV计算方法简洁,但是没有考虑变量每一次取值的差异性与重要性,因此,该文引入了加权调整的变异系数Adjusted_CV,解决带权重的特征稳定性的计算问题。

图1是构建学习能力稳定性的算法模型。

图1 学习能力稳定性算法模型

成绩数据源SDataset如式(2)所示,包括m个学生,n次成绩。

SDataset=[s1,s2,…,sm]=

(2)

其中,Si{i=1,2,…,m}为学生成绩样本,wsi,j为第i个样本第j周的成绩(ws为weekscore的简记),如式(3)所示:

可以通过图1所示的学习能力稳定性算法模型计算si的CV系数值。模型输入层InputLayer接收到按周期采集的n次成绩:weekscore1,…,weekscoren,每次成绩根据其难度系数给予不同权重fi,i的取值为1,2,…,n。转换层TransferLayer根据接收到的成绩及权重数据,计算集中趋势度和离中趋势度。集中趋势度采用加权线性平均的形式进行计算,计算结果记为Weighted_Mean(score_stu),如式(4)所示:

(4)

其中,fi为每次任务的难度系数权重,i的取值为1,2,…,n。

离中趋势度的计算采用加权的样本标准差进行计算,其中n为样本容量,即当前个体成绩数量。计算结果记为Weighted_σ(score_stu),如式(5)所示:

Weighted_σ(score_stu)=

(5)

其中,weekscorei是动态的每周学习成绩,n为时间窗口期内的作业数量。

模型输出层OutputLayer计算最终的学习能力稳定性系数CV值,采用加权的标准差与加权线性均值的比值计算,进而调整的Adjusted_CV计算公式如式(6)所示:

(6)

其中,Adjusted_CV(score)作为个体成绩稳定性原始评价指标,可有效衡量窗口期内学生成绩的稳定性情况,消除量纲与样本容量的影响。Adjusted_CV(score)数值越小,窗口期内学生成绩越稳定地趋近于该学生的平均水平,集中趋势的代表性越好,学生的学习能力越稳定。Adjusted_CV(score)数值越大,平均成绩的代表性也就越差,成绩数值的震荡性越大,因而学生能力的稳定性也就越差。

经过上述算法对Adjusted_CV值的处理,可以得到一系列个体成绩稳定性原始评价数据集合。Adjusted_CV(score)={scorei,i=1,2,…,n},n为样本容量。为了评价个体学生成绩稳定性在全量样本中的位置,此处采用箱线图k百分位数的方式进行离散化,计算方法为p=1+(n-1)×k%,p为k百分位数的位置,此处k的取值为序列[0,25,50,75,100],从而最终产生个体学习稳定性标签。上述完整的学习能力稳定性标签构建算法如算法1所示。

算法1:学习能力稳定性标签构建算法

输入:阶段性在线学习事务数据集C

过程:

(1)Shuffle(C) //随机打乱数据集

(2)For each score_stu inC:

(3) Aggregation(score_stu) //分组聚合个体样本的阶段性评分数据

(4) 根据式(4)计算Weighted_Mean(score_stu) //计算个体线性加权集中趋势度指标

(5) 根据式(5)计算Weighted_σ(score_stu) //计算个体加权离中趋势度指标

(6) 根据式(6)计算Adjusted_cv(scorei) //计算该个体成绩稳定性指标

(7) Add(CV, Adjusted_cv) //将个体成绩稳定性指标Adjusted_cv加入全量样本稳定性指标集合CV

(8)End For

(9)Sort(CV) //对全量样本cv值进行排序

(10)P=1+(n-1)×k% //计算箱线图k百分位数,P为k百分位数位置集合,k取值序列为[0,25,50,75,100],n为样本数

(11)For each cv in CV:

(12) loc=Position(cv,P) //计算个体样本所处百分位数位置

(13)Fi=AssignFlag(loc) //根据个体位置赋予对应标签

(14) Add(F,Fi) //将个体成绩稳定性标签Fi加入全量样本稳定性标签集合F

(15)End For

输出:学习成绩稳定性画像标签集合F

3 学习行为标签模型

学习行为是指学生在线学习的行为习惯,如学习响应习惯、设备访问习惯、登录时间习惯、作业完成习惯等。其中学生对学习任务的响应习惯最具代表性,反映了学生的学习主动性和积极性。下面以学习响应习惯为例,详细阐述行为偏好类画像标签模型的构建算法。图2展示了学习响应习惯偏好行为的事务数据流。学习响应偏好数据的产生主要由任务点、作业、测试、讨论等行为触发,而终端个体会响应该任务,形成访问时间数据流。学习响应习惯偏好标签模型以全量时间数据流为基础,利用箱线图k百分位点方法及概率分布等理论产生。相比较传统的忽略中间时刻敏感度、使用部分响应取平均的方式,这种构建方法更为精准客观。

图2 学习响应习惯偏好行为事务数据流

第一步是单次行为事件的触发,将每一次任务的发布事件序列记为T={trelease,tcheck,tsubmit}。其中trelease、tcheck、tsubmit分别为发布时间、查看时间和提交时间。切片时间段数据记为V={vsensitive,vcomplete},其中vsensitive=tcheck-trelease,vcomplete=tsubmit-tcheck。学习响应敏感度为任务查看时间减去任务发布时间,学习响应完成度为任务提交时间与查看时间之差。每一个个体一次任务的响应值计算公式如式(7)所示:

rj,i=w1*vsensitive+w2*vcomplete

w1+w2=1,i=1,2,…,m,j=1,2,…,n

(7)

响应值rj,i即为响应敏感度和完成度的线性加权平均,m为发布任务数,n为学生样本量,vsensitive为一次任务的学习响应敏感度,vcomplete为一次任务的学习响应完成度,w1、w2分别为敏感度和完成度权重。

对于一次任务,全量学生形成的响应度集合为Ri={r1,i,r2,i,…,rn,i}。

第二步,采用箱线图k百分位数的方式对响应度集合Ri进行离散化,计算方法为p=1+(n-1)×k%,p为k百分位数的位置,k的取值为序列[0,30,70,100]。

第三步,采用众数投票的方式对每一次任务分段结果进行投票计数,取分段频次最大概率值作为最终的学习响应习惯标签。分段概率计算公式如式(8)所示。

(8)

其中,n_pos、n_com、n_neg为第j个样本的积极性、一般、消极性的支持度计数,m为任务数,pj为第j个样本学习响应分段频次概率集合,ppos为响应积极的概率,pcom为响应一般的概率,pneg为响应消极的概率。最终的个体标签取决于概率分布的最大值, maxPj=max{ppos,pcom,pneg}。上述完整的学习响应习惯标签模型构建算法如算法2所示。

算法2:学习响应习惯标签模型构建算法

输入:切片时间事件数据集C

过程:

(1)For eachTiinC.T: //遍历学习任务数据集

(2) For eachSjinTi.S: //遍历第i次任务的个体样本学习数据集

(3)Sj.vsensitive=Sj.tcheck-Sj.trelease//计算样本j的任务敏感度

(4)Sj.vcomplete=Sj.tsubmit-Sj.tcheck//计算样本j的任务完成度

(5) 根据式(7)计算Rj,i//计算个体样本j的第i次任务的响应值

(6) Add(Ri,Rj,i) //将个体任务响应值Rj,i加入全量样本响应值集合R

(7) End For

(8)P=1+(n-1)×k% //计算箱线图k百分位数,P为k百分位数的位置集合,k的取值为序列[0,30,70,100],n为个体样本数

(9) For eachRj,iinRi:

(10) loc=Position(Rj,i,P) //计算个体样本j所处百分位数位置

(11) MFj,i=Flag(loc) //计算样本j第i次任务的标签

(12) Add(MF,MFj,i) //将样本j第i次任务标签MFj,i加入全量样本任务积极性标签阶段性集合MF

(13) End For

(14)End For

(15)For each MFjin MF:

(16) 根据式(8)计算Pj={Ppos,Pcom,Pneg} //计算个体学习响应分段频次概率集合

(17)Fj=max(Pj) //生成个体学习响应习惯标签,个体标签取决于概率分布的最大值

(18) Add(F,Fj) //将个体响应习惯标签Fj加入全量样本响应习惯标签集合F

(19)End For

输出:学习响应习惯标签集合F

4 实验结果与分析

实验数据通过学习通系统在线数据采集,并结合教务系统历史成绩等辅助信息进行人工标注。利用调整的线性加权变异系数算法进行学习能力稳定性模型实验,部分抽样数据及处理结果如表1所示。表中,wsi表示周次,Linearwei_CV表示调整后的CV值,Lw_CV_Quan表示样本所处分位点,tra_tendency表示样本成绩平均值。

表1 调整的线性加权变异系数算法处理结果示例

从表1可以看出,序号为19*****04、19*****27的两个样本在文中所采用的变异系数方法中系数值分别为0.02、0.05,在全量样本中位于第Q1分位点处,成绩稳定性都很高,4号样本成绩高且稳定在98.69附近,27号样本成绩低且稳定在均值67.13附近。19*****02在全量样本中位于第Q2分位点处,成绩稳定性良好,在均值附近有一定的波动,但与均值的偏差不大。19*****26、19*****07,在全量样本中位于第Q3分位点处,成绩稳定性一般,震荡较明显。19*****28在全量样本中位于第Q4分位点处,成绩稳定性差,各次成绩与平均值70.56的偏差较大,震荡明显。

利用调整的线性加权变异系数Adjusted_CV算法与传统的变异系数算法进行学习能力稳定性对比实验,模型效果如图3所示。相较于传统的变异系数算法,调整权重后的Adjusted_CV算法具有更好的拟合效果。

图3 学生学习稳定性加权效果对比曲线

通过学习通系统累计采集16周的在线学习行为数据并进行人工标注,利用箱线图k百分位数及随机变量概率分布的组合方法进行学习响应习惯标签模型实验,部分抽样数据及处理结果如表2所示。表中,Ti_release表示第i次任务的发布时间,Ti_check表示第i次任务的查看时间,Ti_submit表示第i次任务的提交时间,sensitive表示敏感度,complete表示完成度,vote表示样本第i次任务的标签,P(pos)表示样本积极性概率,P(com)表示样本一般性概率,P(neg)表示样本消极性概率,total表示样本响应习惯最终标签。

表2 箱线图k百分位数及随机变量概率分布方法处理结果示例

从表2可以看出,19*****02、19*****04、19*****26、19*****28四个样本对历次任务响应比较积极,其中19*****02积极响应的占比达88%。从上述样本的过程细节数据来看,积极响应的个体样本历次任务的完成度较为及时。19*****27、19*****07号样本响应程度分别为一般和消极,占比分别为63%、50%。从这些样本的过程细节数据来看,此类样本单次任务响应敏感度和完成度较差,尤其是19*****07号样本虽然有时查看任务及时，但是执行力很差，有严重的拖沓习惯。

通过基于箱线图k百分位数及随机变量概率分布的方法可以得出学生响应偏好识别结果的混淆矩阵,如图4所示。从图中可知,方法的准确率为83%,识别效果良好,能够很好地刻画个体的响应习惯偏好。

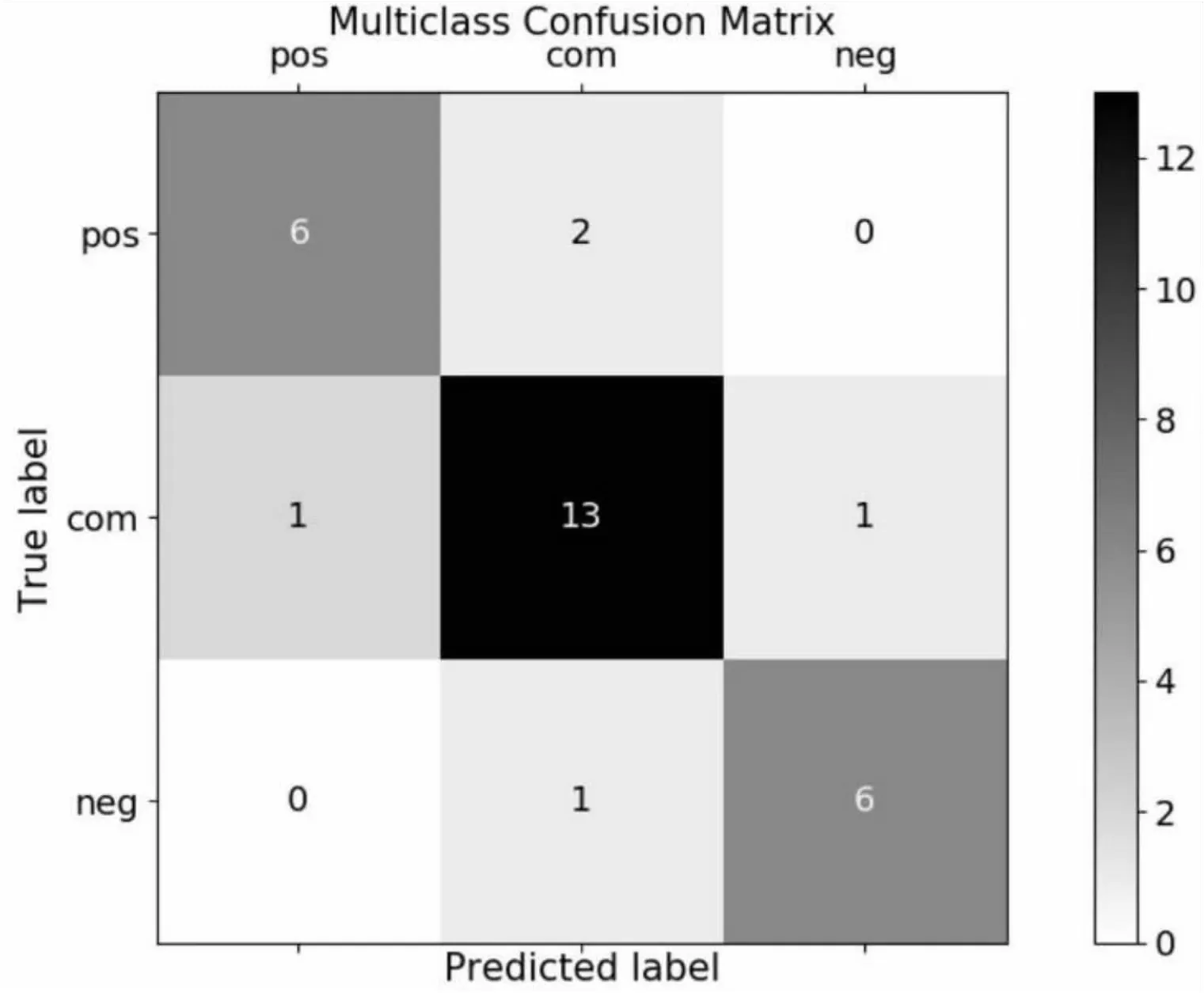
图4 学生响应偏好识别结果混淆矩阵

5 结束语

混合式学习积累了海量的学生学习数据。充分挖掘和利用这些学习过程和学习结果数据,实施学生学习画像是面向未来型教育的一个重要研究领域。学习画像能够很好地刻画学生在学习能力、学习行为和学习成效等方面的特征,实现学生群体的划分[17-18],通过数据驱动更好地为个性化学习规划学习路径[19-20]。学习画像的关键在于对学生学习各个特征维度的标签模型进行构建,从数据的分析结果中提炼出合适的标签来对目标对象的学习特征进行标识。文中提出的一种调整的线性加权变异系数算法,以及对偏好随机变量概率分布理论和箱线图k百分位数方法的应用,成功地构建了学习画像中最关键的学习能力和学习行为两个维度的标签模型。实验结果的对比分析也证明了这种构建方法的合理性和有效性。在后续模型优化过程中,可以考虑扩充数据维度、调整过程权重等方式进一步优化模型效果。