基于小波分解的颅脑动态电阻抗监测中体动干扰实时处理方法研究

陈晓飞，张 戈，王辉林*

（1.联勤保障部队第980 医院医学工程科，石家庄 050051；2.联勤保障部队第980 医院放射诊断科，石家庄 050051）

0 引言

颅脑动态电阻抗断层成像（electrical impedance tomography，EIT）是一种无创、低成本、可连续监护的生物医学功能成像技术，在脑损伤等疾病的早期诊断方面有着良好的应用前景[1-2]。动态EIT 系统通过均匀安放在头部的16 个电极，在2 个不同的时刻向颅脑施加安全电流激励并测量边界电压，并利用一定的算法根据边界电压重构出2 个时刻间颅内的阻抗变化分布[3]。为了保证重构图像的真实有效，参考帧时刻和前景帧时刻的边界电压差应尽可能只来自于颅内阻抗变化，而良好稳定的数据采集过程是满足这一需求的首要条件[4]。然而，在长时连续监护的过程中，电极易受临床上的体动因素如患者的体动（如摆头、翻身）以及医护人员的护理操作等的影响，使得电极-皮肤的接触状态发生改变，从而在边界电压的测量中引入体动干扰，影响重构图像的质量[5-7]。因此，需要对信号中的体动干扰进行处理。

体动干扰是人体生理相关光、电信号采集过程中的常见问题。以是否需要额外的参考信号输入为标准，可将体动干扰处理方法大致分为2 类：第一类为基于自适应滤波器的处理方法[8-9]。其特点在于需要额外的输入信号作为信号处理的期望，以此作为体动干扰或理想信号的先验信息再对干扰信号进行处理。此类方法要求硬件设备具备相应的参考信号采集功能，因此其适用范围受到一定限制。第二类处理方法主要包括维纳滤波法[10]、信号相关提升法[11]、卡尔曼滤波法[12]、主成分分析法[13]、独立成分分析法[14]等。以上方法不需要额外的输入信号，而是通过利用信号的时域、空域或频域特征，或采用奇异值分解等方法，对体动干扰信号进行检测、分离。然而，上述方法均有其特定的使用前提，并且难以进行实时处理[15]。

小波分解法是一种通过分析信号的时频特性来检测并处理体动干扰成分的信号处理方法。最早Sato 等[16]利用小波分解的方法实现了颅脑近红外光光谱检测中体动伪影的精准识别。后续研究人员在此基础上通过对对应体动干扰的小波分解系数进行处理，实现体动干扰的抑制[9，17-18]。Yang 等[19]通过小波分解的方法对肺部呼吸EIT 监测中体动干扰信号进行处理，表明小波分解法在阻抗监测信号的质量提升方面也有着良好的应用潜力。目前，将小波分解方法应用到颅脑电阻抗监测中的文章鲜有报道。

基于此，本研究利用小波分解的方法处理颅脑EIT 监测中的体动干扰信号。与传统小波信号处理的方法不同，本研究拟基于不同来源信号小波分解系数的分布特征对体动干扰信号进行检测，并采用垒墙式的计算策略实现该处理方法的实时运行。本方法摆脱了传统小波处理方法在软硬阈值选择上的局限性，通过概率分布的方法实现小波分解系数的动态选择，提高了数据处理的效能。

1 方法

1.1 EIT 的数据采集

本研究使用的颅脑EIT 系统需要等间距受试者头部环贴16 个电极，采用对向激励、邻近采集的工作模式进行边界电压数据的测量，数据采集流程如图1 所示。该数据采集模式下单次激励可得到12 个边界电压数据，遍历所有电极构成完整的一帧测量数据[20]。

图1 对向激励-邻近测量模式下EIT 数据采集示意图

1.2 基于小波分解的体动干扰处理

通常颅脑EIT 监测采集得到多个通道平缓慢变的时间序列边界电压信号[21]。当体动干扰发生时，边界电压信号发生剧烈波动，与脑电等人体生理相关电信号中体动干扰信号的形态相似，使得使用小波分解的方法来区分正常EIT 信号与体动干扰成为可能。

对于动态EIT 而言，其重构过程可以简略表示为

式中，y表示阻抗变化图像；B表示重构矩阵；xf表示前景帧边界电压数据；xb表示参考帧边界电压数据。体动干扰会体现在前景帧xf中并影响重构结果。

前景帧数据中同时包含了正常的EIT 信号和体动干扰信号，可以表示为

式中，xf（t）表示时间序列的前景帧边界电压信号；xf0（t）表示正常的EIT 边界电压信号；xf0（t）表示正常的EIT 信号；ε（t）表示体动干扰信号。使用Mallet 方法进行小波分解的形式可以将原始信号表示为[22-23]

从图3可以看出，试验期间，不同覆盖条件下，水温平均日较差从高到低为单层薄膜覆盖、对照、双层薄膜覆盖；单层薄膜覆盖条件下，30、60 cm水深的池子水温平均日较差分别为5.9、5.8℃， 相差不大；双层薄膜覆盖条件下，30、60 cm水深的池子水温平均日较差分别为2.5、2.2℃，同样相差不大；但露天条件下，60 cm 水池的变化范围在 2.3～7.0℃，平均日较差为4.3℃，比30 cm的水池高1.1℃。双层薄膜覆盖、露天处理的日较差变化趋势基本一致，表现为晴天条件下日较差较大，多云次之，阴天最小；而单层薄膜覆盖表现为多云条件下日较差较大，晴天次之，阴天最小。

式中，øjk（t）=2j/2ø（2jt-k），表示重构尺度函数；ψjk（t）=2j/2ψ（2jt-k），表示重构小波函数；j和k分别表示小波分解层数和尺度平移系数；v表示尺度分解系数；wj表示第j层小波分解系数，并且有

式中，g（n）和h（n）分别为高通滤波器和低通滤波器。

任意时间序列信号的小波分解系数均可以使用包含2 个独立的高斯分布模型的混合高斯分布模型来描述其分布特征[24-25]。2 个高斯分布模型的均值均为0 但方差不同。方差较小的高斯模型代表幅值变化幅度较小的小波分解系数分布特征，方差较大的高斯模型则代表幅值变化幅度较大的小波分解系数分布特征。与体动干扰信号相比，正常的颅脑EIT 信号在时间序列幅值改变更为缓慢，因此其对应的小波分解系数方差更小，在0 均值周围波动范围更窄。所以，可使用小方差的单个高斯分布模型来描述正常颅脑EIT 信号小波分解系数的分布[24]。对应wjk的分布可以表示为wjk~N（0，σ2j）。其中每层的方差σ2j估计依据绝对中位差确定。绝对中位差对数据集中的异常值不敏感，具有良好的稳定性。在颅脑EIT 数据采集过程中，体动干扰表现为叠加在正常颅脑EIT 信号上的离散异常值，其对应的总体分布方差与期望估计的先验正态分布方差不同。少量体动干扰的发生不影响对正常颅脑EIT 信号小波分解系数先验高斯分布σ2j的估计结果。σ2j的具体计算公式为[26]

每个wjk对应一个曲线下面积pjk，将其称为拒绝概率，表示wjk并非来源于预定义正态分布总体的概率，具体定义为

式中，|wjk|/为标准化后的正态分布；其中x∈R，为正态分布的积分函数。

参考统计置信区间定义，设定置信概率阈值α，若pjk≥α，则表明wjk并非来源于预定义正态分布总体，其对应的原始数据为体动干扰信号，否则对应正常的颅脑EIT 信号，基于此对wjk进行处理，具体可表示为

包含体动干扰的wjk来源于先验正态分布N的事件发生概率位于置信区间外，其对应的拒绝概率应大于置信概率阈值，因此受体动干扰影响严重的分解系数置零，从而抑制体动干扰成分。阈值α决定了对体动干扰的判定标准和抑制程度，当α→0 时，则对所有的小波分解系数均不作处理。本研究中设置α=0.9。各参数定义如图2 所示。

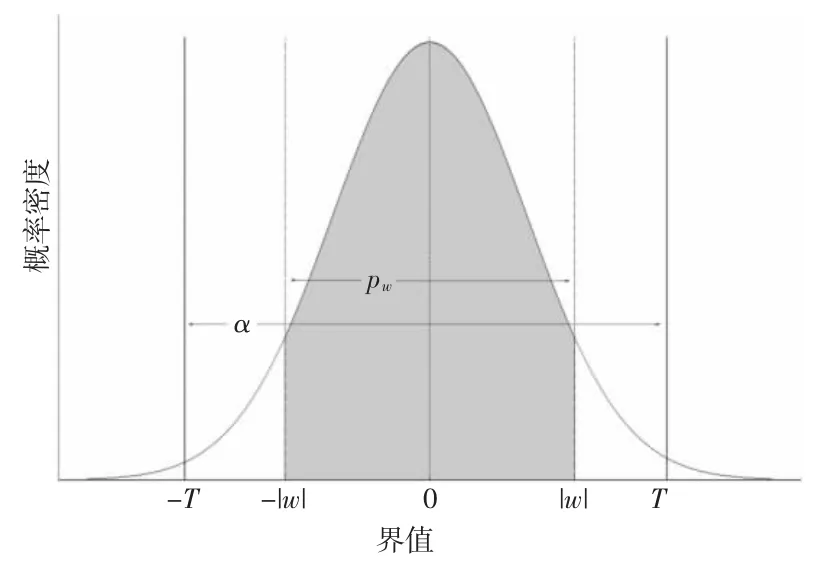
图2 利用小波拒绝概率筛选体动干扰对应的小波分解系数方法示意图

对小波分解系数的处理与否取决于体动干扰的严重程度。体动干扰的严重程度具体定义为当前尺度下小波分解系数超出预定义阈值α的数量。定义数据集合和，其中I为指示函数。设置尺度系数j，得到数据集合{ψj}，进行体动干扰筛选处理的小波分解层标记为ψj，processed，{ψj，processed}的和不应小于{ψj}的90%，以保证体动干扰处理的效果，并据此反向确定小波分解的层数。

1.3 实时小波计算

通常离散小波分解采用的是Mallet 方法，其通过滤波器族以逐级递推的方式进行计算。在进行离线小波分解计算时，一般将全部数据一次性读入后再逐层分解。然而，由于分解和重构滤波器的长度有限，单次卷积计算所需要的数据长度也是有限的，数据长度满足向下一层分解时即可进行小波分解运算。基于此，饶贵安等[27]提出了一种垒墙式的小波分解计算方法（如图3 所示），随着数据的不断读入，同时进行小波分解的计算，数据长度满足计算需求即向下进行一次小波分解计算，计算流程整体横向发展。

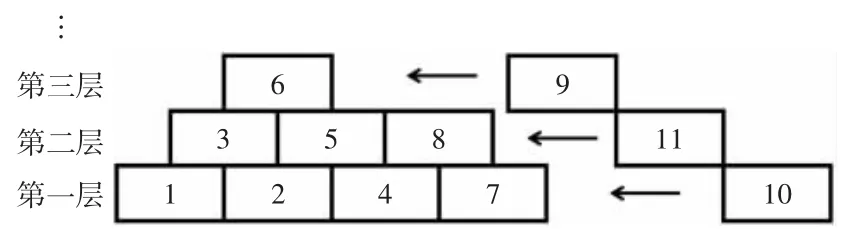
图3 垒墙式小波分解示意图

1.4 实验验证设计

为了验证上述方法的有效性，开展仿真实验和人体实测数据实验研究。

1.4.1 仿真实验

设计以下含高斯白噪的复合频率正弦信号模拟颅脑EIT 信号：

式中，n=4；ω=2πf；μ 为正弦波的振荡幅度；σ（t）为高斯白噪声，模拟信号采集过程中的系统噪声；γ为噪声幅值，设置为1%水平。xsimulate（t）的幅值控制为（-1，1）。正弦波参数的设置涵盖可能存在的人体生理信号及其他干扰，具体设置参照文献[28]，其中包括：（1）同步心率信号，f1=1 Hz，μ1=0.4；（2）同步呼吸信号，f2=0.25 Hz，μ2=0.4；（3）低频混叠信号，f3=0.1 Hz，μ3=0.4；（4）极低频混叠信号，f4=0.01 Hz，μ4=0.5。仿真信号共包含1 000 个数据点。

向上述仿真信号中添加尖峰信号模拟体动干扰。本研究设置如图4 所示的4 种不同类型的尖峰信号，分别为MA1、MA2、MA3、MA4。4 种尖峰信号与原始信号叠加得到混合信号xmix。采用均方根误差百分比（percent root difference，PRD）、Pearson 相关系数（r）、决定系数（R2）3 个量化指标分别对混合信号x和处理后信号y与原始信号xsimulate的一致性进行评价，量化评估模拟体动干扰的处理效果。其中PRD 反映2 组数据的离差特征，PRD 越小则2 组数据的背离程度越小；r评价2 组数据的相似程度，r越大则2 组数据越相似；R2反映在空间距离上y（t）向x（t）的逼近程度，最大值为1，越接近1 说明y（t）对x（t）的拟合程度越好。具体的计算公式如下：

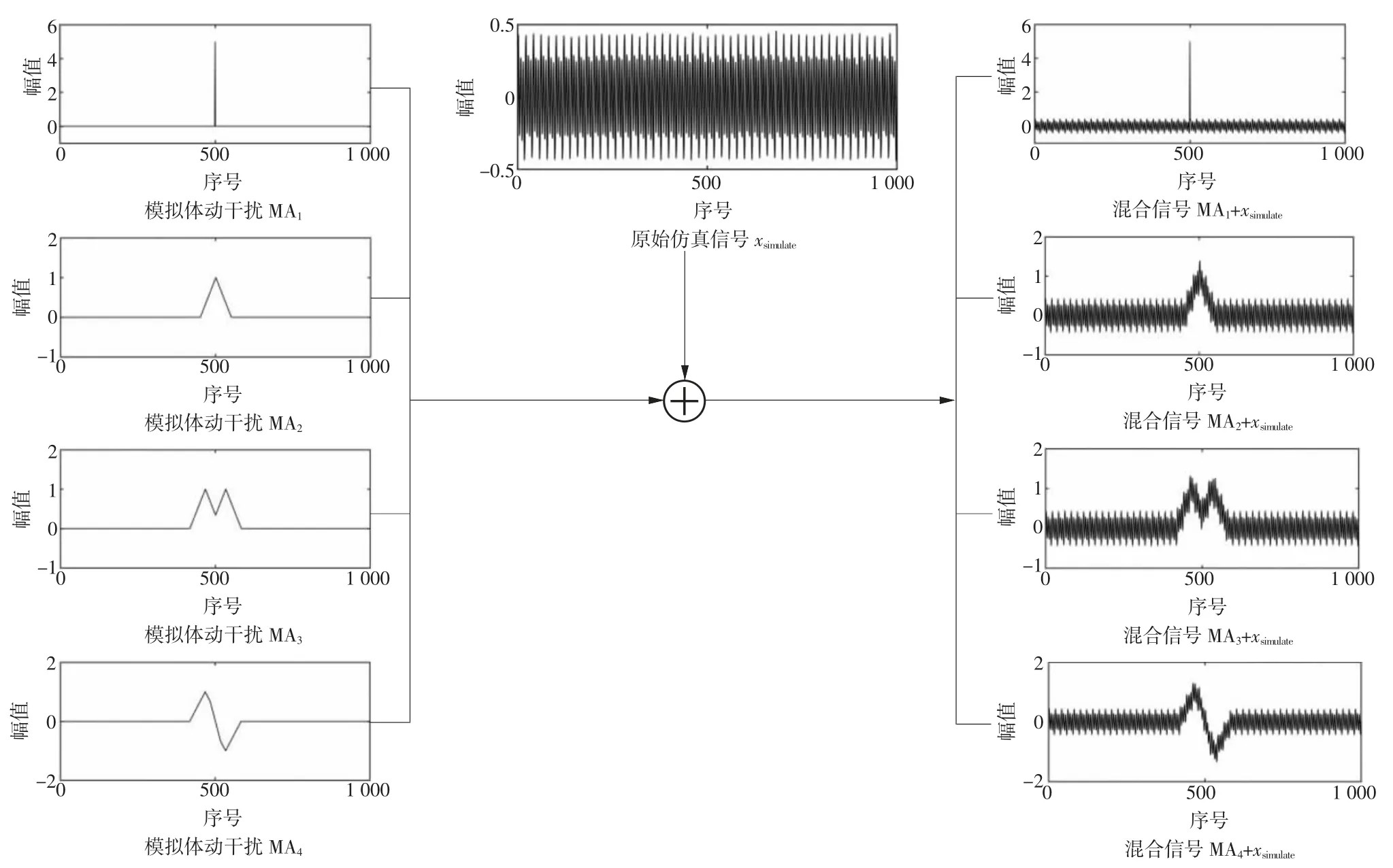
图4 仿真信号及体动干扰设置示意图

式中，x（t）和y（t）为要比较的时间序列信号，N为数据长度。对于本研究，x（t）为不含模拟体动干扰的原始信号xsimulate（t），y（t）为处理前后的含体动干扰信号xmix（t）。

1.4.2 人体实测数据实验

被试的纳入标准如下：（1）头皮表面无创伤；（2）非危重症，无颅骨骨折；（3）意识清醒，可配合进行数据采集；（4）无其他不适合进行颅脑EIT 数据采集的情况。最终纳入的被试为2018 年3 月于空军军医大学附属医院神经外科就诊的2 例男性患者（年龄分别为18 岁、53 岁）的数据，均为轻型头部外伤后留观。将16 个进行过消毒处理的杯状电极涂抹导电膏后，均匀环贴于患者头部。数据采集使用FMMU-EIT5 数据采集系统，激励电流为500 μA，激励频率为50 kHz，数据采集速度为1 帧/s。在数据采集开始前，将16 个进行过消毒处理的杯状电极涂抹导电膏后，均匀环贴在患者头部。数据采集过程中患者躺在病床上，对患者的体动和医护人员的护理操作不做干涉。人体数据采集已获伦理委员会批准。

2 结果

2.1 仿真实验

本研究中数据处理方法对仿真信号的处理效果如图5 所示。仿真实验采用db6 小波，分解层数为10。图5（a）、（b）、（c）、（d）为图4 中对应的混合信号经过小波处理后的结果。在信号形态上，尖峰信号模拟的体动干扰得到了有效抑制，处理后的数据与原始数据高度相似。量化评估体动干扰抑制方法的结果见表1。不同指标的改善程度与干扰信号类型密切相关。对于MA1和MA2，ΔR2大幅上升，而对于MA3和MA4，则Δr改善最明显。除MA2以外，ΔPRD 的改善均超过70%。

表1 混合信号处理前后PRD、r 及R2 量化指标的比较

图5 仿真实验结果

表1 为混合信号处理前后均方根误差百分比PRD、Pearson 相关系数r、决定系数R2量化指标的比较。ΔPRD、Δr、ΔR2为对应指标在数据处理后相较于处理前的百分比改变。

2.2 人体实测数据实验

人体实测数据的处理结果如图6 所示。由于颅脑EIT 有192 个通道的有效数据，因此需要对192个通道分别进行处理。针对纳入的2 名被试，分别截取650 帧和280 帧长度的临床实测数据，其中包含了数个观测到的体动干扰。选用db4 小波，分解层数为6，对数据进行处理，处理结果如图6 所示。对比处理前后的信号波形，原始数据中包含的体动干扰都得到抑制，数据的连续性明显提升。

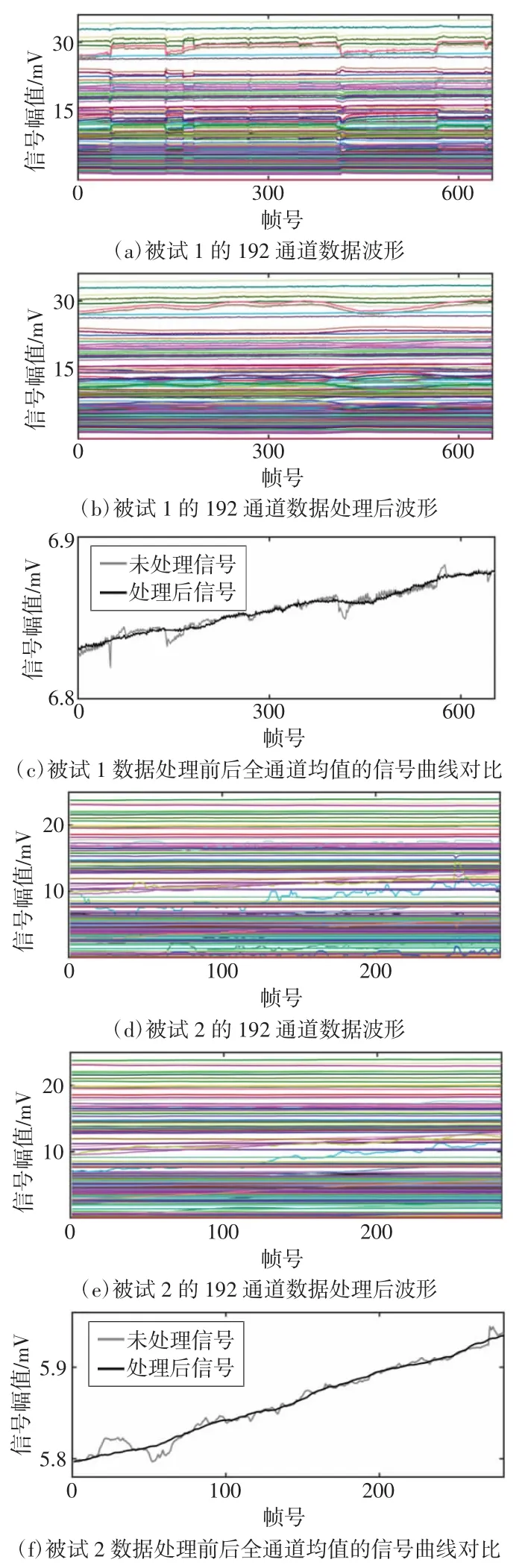
图6 人体实测数据处理结果

颅脑EIT 图像监护需要将边界电压数据重构为二维阻抗分布图像，因此对处理前后的数据进行图像重构以检验干扰抑制效果。图像重构使用基于Matlab 2016b 的EIDORS v3.8 工具箱，图像重构方法为高斯牛顿法。图7、图8 分别为被试1、被试2 的电压均值曲线图。图9~12 为被试1 数据处理前后的图像重构结果对比，图13~15 为被试2 数据处理前后的图像重构结果对比。体动干扰导致重构图像出现明显的体动伪影[如图9（a）、10（a）、11（a）、12（a）所示]，经小波方法处理后图像的均匀性显著提升[如图9（b）、10（b）、11（b）、12（b）所示]。在相同坐标尺度范围下，数据处理后的重构图像三维幅值分布更加平滑。同样的，从重构图像重构值变化范围上看，在相同尺度下，处理后数据的重构图像上的伪影基本消失，重构图像的幅值更为平滑。

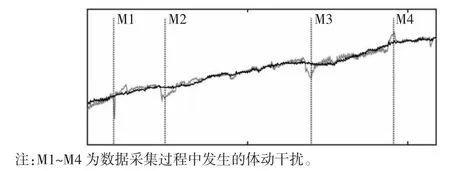
图7 被试1 电压均值曲线

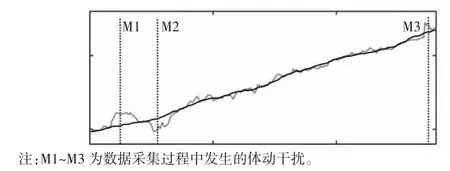
图8 被试2 电压均值曲线

图9 被试1 体动干扰M1 处理前后的重构图像及其三维幅值分布

图10 被试1 体动干扰M2 处理前后的重构图像及其三维幅值分布

图11 被试1 体动干扰M3 处理前后的重构图像及其三维幅值分布

图12 被试1 体动干扰M4 处理前后的重构图像及其三维幅值分布

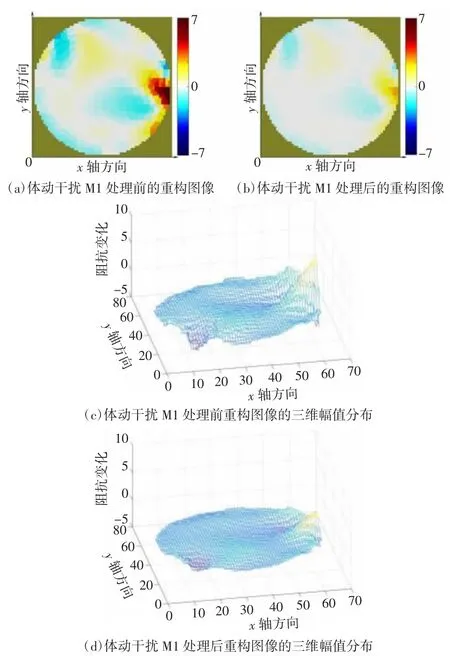
图13 被试2 体动干扰M1 处理前后的重构图像及其三维幅值分布

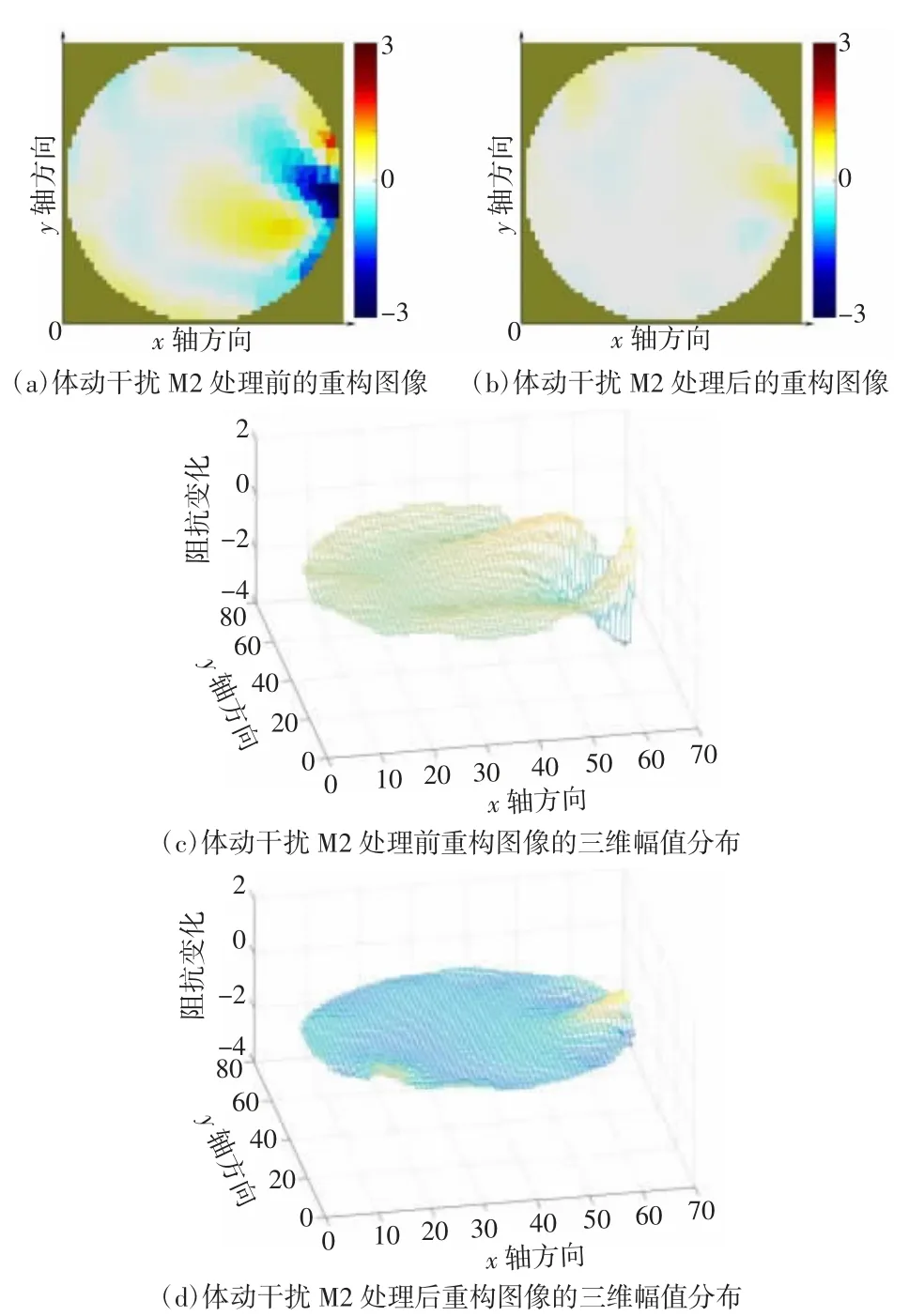
图14 被试2 体动干扰M2 处理前后的重构图像及其三维幅值分布

图15 被试2 体动干扰M3 处理前后的重构图像及其三维幅值分布

3 讨论

本研究采用小波分解的方法对颅脑EIT 数据采集中的尖峰型体动干扰进行处理。与既往小波处理方法不同的是，本研究放弃了既往研究中需要手动确定硬阈值或软阈值的方法，采用了概率计算的策略进行体动干扰信号的筛选。基于正常颅脑EIT 信号的小波分解系数构建代表其总体的高斯分布模型，针对单个小波分解系数，计算其在先验高斯模型下对应的曲线下面积，即为拒绝概率。如果该小波分解系数位于预设定的先验高斯分布置信区间外，则其对应的拒绝概率应大于预设的概率阈值，由此实现体动干扰成分的筛选并加以处理。该方法仅需设定统一的概率阈值，不需要为每层小波分解系数单独设置特定阈值，大大减轻了算法设计的负担，提高了体动干扰的检测效能。特别是对于EIT 信号这样的多通道数据而言，该方法尤其适用。人体实测数据实验表明，该方法可有效抑制时间序列信号中的体动干扰成分，恢复信号的连续性，减轻重构图像伪影。

前期文献对于体动干扰信号的形态特征进行过经验性总结，研究人员将生理相关光电信号采集中的体动干扰总结为时间序列信号中幅值超出正常信号范围的快速、剧烈变化信号成分，并且与正常信号相比更缺乏周期性[16]。在颅脑EIT 信号中，与平缓慢变的正常信号相比，体动干扰主要包含高频成分。因此，根据小波函数与信号间断点的卷积特性，体动干扰部分信号对应的小波分解系数表现为局部的模极大值[19]。这种小波分解系数模值的差异是使用混合高斯分布模型描述小波分解系数分布特征并对干扰信号进行鉴别的基础。

本研究仍存在一定的不足：本研究中提出的基于小波分解的尖峰型体动干扰处理方法在干扰界定的阈值上具有较好的灵活性，但其大范围推广应用仍需进行更多的临床实测数据验证。此外，临床上体动干扰的发生有可能存在尖峰型干扰与其他类型体动干扰混叠的场景，降低本研究中小波方法的处理效能。因此，在下一步的研究中将收集更多的临床体动干扰类型数据，对本研究中处理方法进行针对性的改进，增强鲁棒性，从而提升颅脑EIT 的临床实用性与适用性。

综上，本研究提出的基于小波分解系数统计特征的颅脑EIT 体动干扰处理方法避免了对每次小波分解结果设定具体阈值，而是通过设定置信概率区间的方法实现体动干扰成分的筛选与处理，特别适合颅脑EIT 多通道数据采集的应用场景。实验结果表明，该方法可有效抑制体动干扰成分，恢复正常的图像监护。