基于优化支持向量回归算法的锂离子电池可用容量估计
陈 峥,陈 洋,申江卫,夏雪磊,沈世全,肖仁鑫
(昆明理工大学交通工程学院,云南 昆明 650500)
锂电池具有寿命长、充电速度快、无记忆效应等优点,因此被广泛用作纯电动汽车和混合动力汽车的储能器[1]。锂电池在使用过程中其性能会随着充放电循环次数的增加而逐渐退化,具体表现为内阻增加以及可用容量减少[2]。当电池可用容量衰退到额定容量的80%时,电池达到寿命终止(end of life,EOL),若继续使用电池,则更容易发生故障,存在较高安全风险[3]。因此,在使用过程中准确估算锂电池容量,对电池高效和安全运行具有重要意义[4]。
目前大概有三类方法被广泛应用于电池可用容量准确估算:直接测量法、基于模型的估算、基于数据驱动的估算[5]。直接测量法通过对电池进行完整充放电,利用安时积分法计算电池当前可用容量,该方法简单、精确,然而该方法仅适用于离线电池的容量标定,且耗时较长,难以实现车载条件下的可用容量测量[6]。基于模型的方法是通过建立电池模型并获取模型参数,进而根据模型参数估计电池可用容量,常用的模型有电化学模型、经验模型等。电化学模型是从电池内部化学反应的角度建立模型来反映电池在退化过程中表现出的规律[7]。经验模型是通过分析大量的电池充放电实验数据,得出电池容量与电池各参数的变化规律,进而建立容量与各参数之间的函数关系[8-9]。基于模型的方法能较好反映电池的物理特性,但是构建一个精确的电池退化模型较复杂,模型精度依赖于模型参数的准确辨识,而模型参数容易受到温度、老化等多因素耦合影响[10]。
基于数据驱动的估算方法不需要构建复杂的电池模型,可以通过测量得到的电压、电流和温度等数据来自主学习电池容量与外部特性的非线性关系,具有较高的可迁移性、鲁棒性与泛化性[11]。常用的数据驱动方法包括长短期记忆网络(long shortterm memory,LSTM)、支持向量机(support vector machine,SVM)、支持向量回归(support vector regression,SVR)、高斯过程回归(Gaussian process regression,GPR)等。文献[12]采用LSTM 来估计电池的可用容量,选取电池表面平均温度、电池充电内阻以及增量容量曲线峰值作为老化特征和模型输入,最大误差为2.84%,但LSTM模型仍存在梯度消失、训练时间长以及对训练数据要求高的问题。文献[13]采用卷积神经网络模型从电池电压和电流数据中自动学习电池老化特征,并实现了可用容量的精确估计。文献[14]采用鲸鱼优化算法优化GPR 模型并进行电池可用容量估计,所建立的优化GPR 模型能够基于较少训练数据实现电池容量的精确估算,最大误差低于1.56%。文献[15]基于改进双最小二乘支持向量机方法和Box-Cox 变换,进行锂离子电池的可用容量及剩余循环寿命的协同估算,可用容量估计误差小于1.44%,但是Box-Cox变换的阈值给电池容量估算引入了新的不确定性。文献[16]提出了一种基于时间规整图来提取健康特征参数的方法,并使用SVR 模型估计电池可用容量,最大容量估计误差小于3%。目前使用传统的SVR 估算电池可用容量时,依然存在估算时间长、不能找到全局最优等问题。因此对传统的SVR在参数寻优的方法上,需进一步深入研究从而提高估算效率。文献[17]提出了一种将麻雀优化算法(sparrow search algorithm,SSA)用于微电网容量的优化配置的应用,提高了系统供电可靠性及整体经济效应。在参数寻优方面,SSA算法凭借其收敛速度快、寻优精度高等优点被广泛应用于电池的可用容量估计中。
综上,针对传统SVR 算法在处理大样本数据时,参数寻优存在时间耗时长、容易陷入局部最优、对可用容量准确估计不够精准的问题,本工作选用SSA 算法对SVR 进行核函数参数寻优,提出了一种优化支持向量机回归算法,用于准确估计锂电池的可用容量。首先通过分析电池老化数据来提取特征因子,并通过皮尔逊相关系数法分析其关联性;然后利用SSA 对SVR 的超参数进行寻优,并搭建SSA-SVR 电池可用容量估计模型,实现了电池可用容量衰退过程的准确追踪;最后选择不同参数寻优方法以及不同估算模型进行了模型验证,并在不同电池上实现了锂电池可用容量的准确估计,证明了算法的有效性。
1 电池老化实验
本节将介绍电池循环老化实验测试流程,并通过分析老化数据,提取能够表征电池容量衰减的特征因子,然后通过皮尔逊相关系数验证所选取特征因子与电池可用容量衰退的相关性。
1.1 电池老化实验
本工作使用的电池数据来源于一个较大的电池数据库[18],该数据库收集了各种商用LFP/石墨电池的循环寿命测试数据。从中选取了5块电池,分别表示为电池1、电池2、电池3、电池4 和电池5。该电池正极材料为磷酸铁,负极材料为石墨,标称容量为1.1 Ah,额定电压为3.3 V,电压工作范围为2.0~3.6 V。电池老化实验流程遵循相同的充放电流程,其中充电阶段首先是C1-C2 多段恒流充电,然后是恒流-恒压充电。C1 和C2 是指第一段和第二段恒流充电,当电池荷电状态(state of charge,SOC)达到80%时,多段恒流充电停止,之后静置10 s,然后1 C 恒流充电至3.6 V,最后以3.6 V 恒压充电至0.05 C。充电完成后对电池使用4 C 恒定电流放电至2 V,当电池可用容量衰减到初始容量的80%时老化实验终止。电池老化实验流程如图1所示。

图1 电池老化实验Fig.1 Battery aging experiment
图2 展示了通过循环寿命测试得到的5 块电池的可用容量衰退曲线。由图2可知,随着电池充放电循环的增加,其可用容量整体表现出逐渐下降的趋势;5 块电池的可用容量衰退曲线整体下降趋势相近,表明同一类型锂电池在相似的工作条件下有着相近的衰退规律;电池容量在由100%至90%的阶段,衰退较为平缓,当电池容量衰退到90%以后,衰退明显加快。结果表明锂离子电池的容量衰退过程呈现强非线性特征,这也给电池可用容量的准确预测带来了挑战。因此需要更加充分地分析电池老化数据,从而获得能够更好地表征电池容量衰退过程的特征因子。
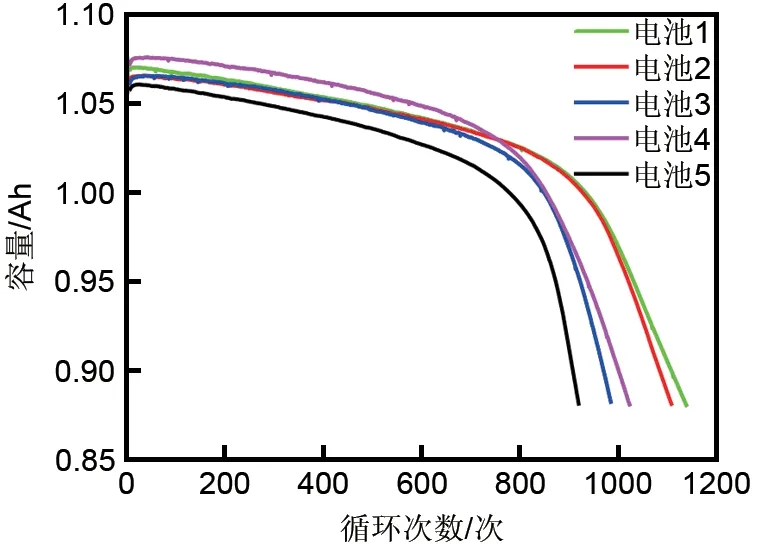
图2 1~5号电池可用容量衰退曲线Fig.2 Available capacity decline curve of cells No.1—5
1.2 老化数据分析及特征提取
将端电压视为容量增量函数,可以得到容量增量(incremental capacity,IC)曲线,该方法被广泛应用于电池可用容量的估计中。IC曲线能够将电池充放电过程中相对平缓的电压平台转化为变化趋势明显的IC 曲线,并且不需要完整的充放电数据,能够从实车原始数据直接提取,具有较好的优势。IC曲线计算公式为:
式中,Q为充放电容量;V为电池端电压;t为时间。当取较短的时间间隔时,由式(1)可得:
通过高斯滤波处理后的容量增量曲线如图3所示。由图3可知IC曲线具有明显的峰值点,随着电池循环次数的增加,峰值点高度不断降低并向左偏移。为进一步验证其与电池可用容量衰退的关系,提取1~5号电池的IC曲线峰值绝对值与循环次数的关系,如图4所示。由图4可以看出随着循环的不断进行,IC曲线峰值绝对值整体呈下降趋势,且在前800 个循环下降较为平缓,当循环次数达到800 次后,下降趋势加剧。这与图2中电池可用容量的衰减趋势呈现强一致性,因此提取IC曲线峰值绝对值作为表征电池可用容量衰退的特征因子,记为F1。
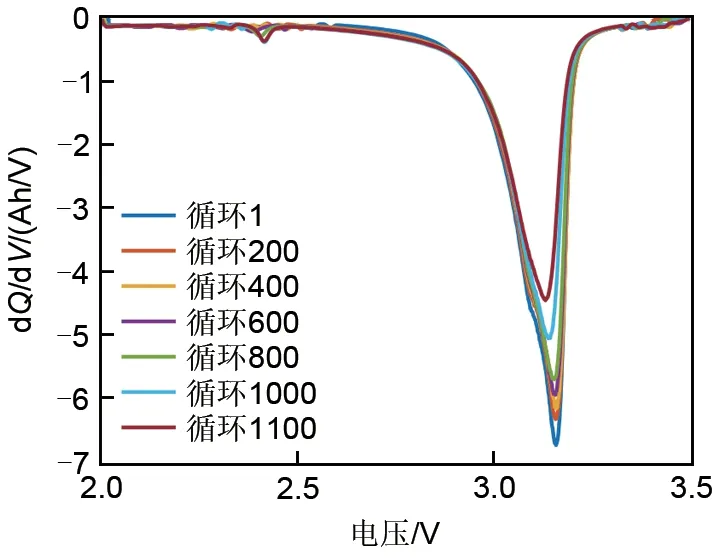
图3 电池1不同循环的容量增量曲线Fig.3 The variation curves of discharge incremental capacity at different cycle numbers for cells No.1

图4 电池1~5容量增量曲线峰值绝对值Fig.4 The peak absolute value of capacity increment curve for cells No.1—5
由图3还可以看出,随着电池老化的进行,容量增量曲线峰值对应电压不断减小。为探究其与电池可用容量衰退的关系,提取1~5 号电池IC 曲线峰值对应电压与循环次数的关系,如图5所示。由图5 可以看出,随着循环的不断进行,在前1~800 个循环内,IC 曲线峰值对应电压基本保持稳定,当循环次数达到800次后,电池IC曲线峰值对应电压迅速减小,这与图2中电池可用容量的衰减趋势呈现较强的一致性。所以,将每个循环下的IC曲线峰值对应电压作为一个特征因子,记作F2。
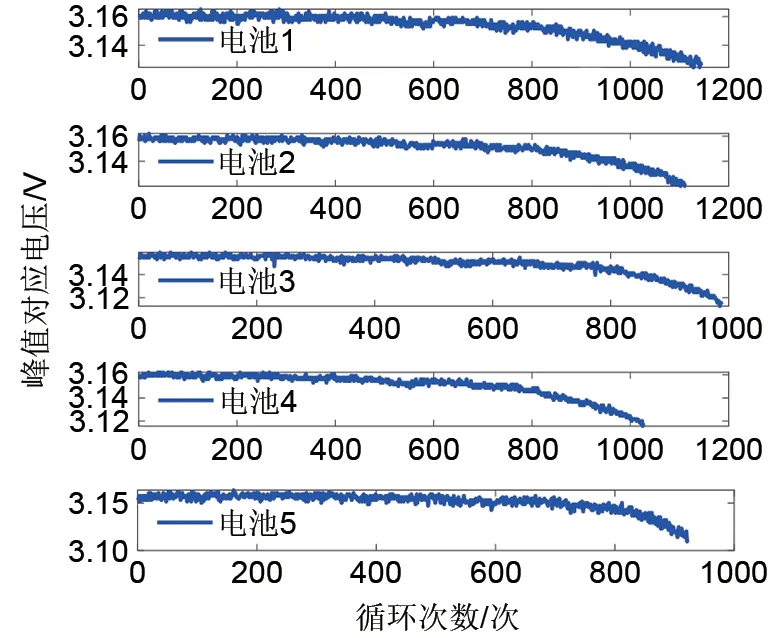
图5 电池1~5 特征因子F2变化趋势Fig.5 Variation trend of characteristic factor F2 of cells No.1—5
1.3 基于皮尔逊相关系数的相关性分析
为了进一步验证所选取的特征因子是否合理,采用皮尔逊相关系数评估其与可用容量之间的相关性。皮尔逊相关系数是表达两变量线性相关程度及方向的统计指标,其绝对值越接近1,表明相关性越强。皮尔逊相关系数计算公式如下
式中,n为样本数;Xi、Yi为样本;、为样本平均值。通过计算,得到所选特征因子与电池可用容量的皮尔逊相关系数如表1所示。
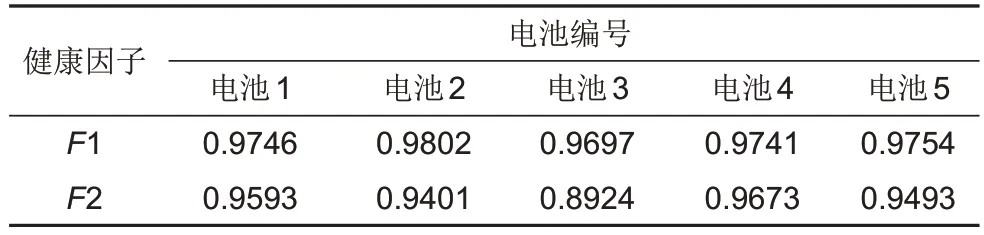
表1 电池容量与特征因子的皮尔逊相关系数Table 1 Pearson correlation coefficient between capacity and features
从表1可以看出,除电池3的特征因子F2的相关系数小于0.9 外,其余特征因子与容量的相关系数均超过0.9,因此可以认为选取的特征因子能较好地反映电池可用容量的衰减。
2 SVR模型以及优化SVR训练
本部分将主要介绍SVR 模型以及SSA 算法原理,并基于SSA-SVR 算法构建了电池可用容量估算框架。
2.1 SVR算法原理
SVR模型是通过最小化总损失和最大化间隔来得出优化后的模型。相较于其他机器学习算法,SVR 基于核函数(kernel function,KF)理论,将高维样本映射到特征空间后再进行回归,能够较好地处理高维线性问题,有效地提高了估算精度。除此之外,SVR模型参数较少,模型训练效率高。而且SVR 方法使用少数的支持向量代替整个样本空间,使得计算最终决策函数时更简便,且有较好的“鲁棒性”。
假定训练样本集为{(xi,yi)|i= 1, 2 …n},其中n为训练样本集的数量,SVR回归函数为:
式中,w和b分别为模型的权重参数以及偏置参数。通过引入拉格朗日乘子将公式(5)转化为求解凸二次优化问题,其中对偶函数和约束条件为:
式中,ω为权重;c为惩罚因子;ξ与ξ*均为松弛因子;ϕ为映射函数;ε为不敏感损失函数;b为阈值;xi、yi为样本。求解式可以得到:
式中,x为样本值;αj和均为拉格朗日乘子;nsv为支持向量个数;K(xj,x)为核函数,本工作使用的RBF核函数为:
式中,g为核函数参数。
2.2 麻雀优化算法
麻雀优化算法是受麻雀觅食行为以及反捕食行为启发而提出的一种智能优化算法,该方法具有设置参数少、操作简单、搜索精度高、寻优速度快以及跳出局部最优能力强等优点。算法具体可抽象为发现者-追随者模型,并加入了侦查预警机制。在麻雀觅食时,一定比例的麻雀当作发现者,用于寻找食物,剩余麻雀当作加入者,在发现者的领导下获取食物。同时一部分麻雀会进行侦查,麻雀在发现捕食者后,会放弃食物。搜索算法流程如图6所示。
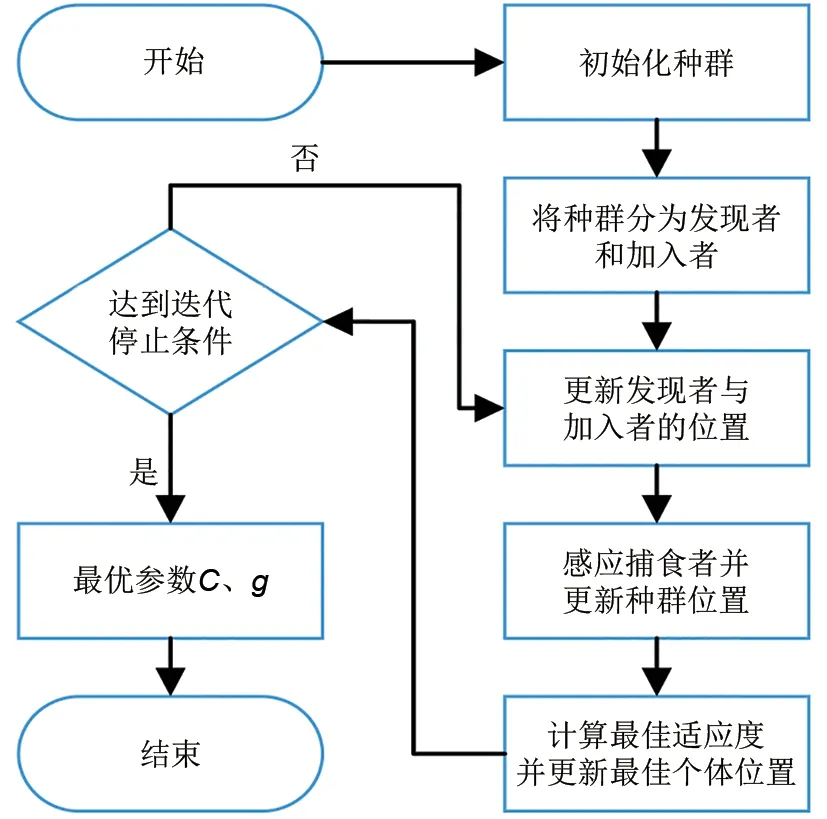
图6 麻雀搜索算法流程Fig.6 Sparrow search algorithm flow
其中发现者的位置更新描述如下:
式中,itermax为最大迭代次数;Xi,j为麻雀的位置信息;α是一个随机数;R2为预警值;ST为安全值;Q是服从正态分布的随机数。L表示一个1行多维的矩阵,其中每个元素都为1。
加入者的位置更新描述如下:
式中,Xp表示最优位置;Xworst表示最差的位置;A是一个1×d的矩阵。
警戒者位置更新描述如下:
式中,Xbest表示最优位置;β、K是都随机数;fi表示麻雀的适应度;fg和fw分别表示全局最佳和最差的适应度。
2.3 SSA-SVR模型训练
在SVR 中,惩罚因子C影响模型的复杂度和精度,而核函数参数g则控制着模型径向的效应范围,是影响SVR 性能的主要因素。传统SVR 对寻找最优C和g的效率低,精度差,故引入麻雀搜索算法,提升参数寻优的效果。SSA 优化SVR 流程如图7所示。首先是通过分析电池老化数据提取特征因子F1、F2,然后用特征因子与对应可用容量组成样本集,并按照比例将样本集分为训练集和测试集。其中训练集用于SSA 对SVR 的参数寻优,并结合最优C和g完成SSA-SVR 模型的搭建及训练。最后利用测试集评估SSA-SVR 模型估计电池可用容量的精度。
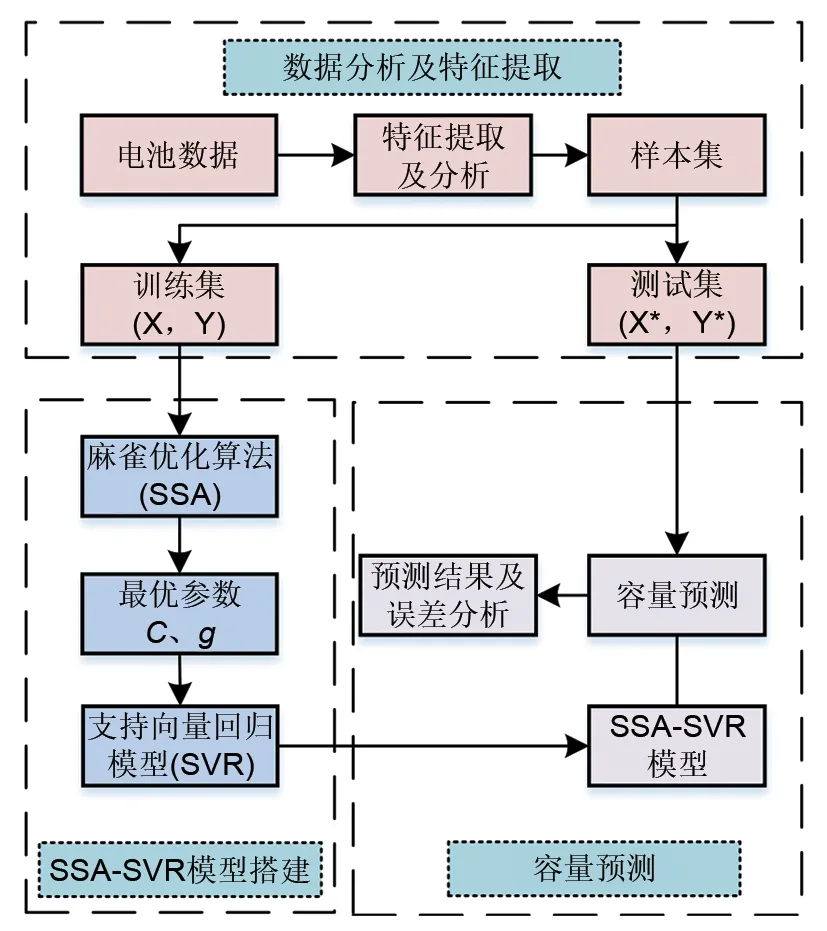
图7 SSA-SVR算法流程Fig.7 Algorithmic flow of SSA-SVR
2.4 性能评价指标
本工作利用判定系数(cofficient of determination,R2)、均方根误差(root mean square error,RMSE)、平均绝对误差(average absolute error,AAE)、最大绝对误差(maximum absolute error,MAE)[19]为评价指标,用来评估电池可用容量估计的准确度。具体计算公式如下:
式中,m为样本数量;yi为真实值;ŷi为预测值;为响应变量均值。其中,R2取值范围为[0,1],越靠近1 说明拟合程度越高,模型质量越好;而MAE、AAE 及RMSE 越小,说明模型估算精度越高。
3 实验验证及结果分析
本部分首先分析了不同长度训练集对模型训练精度以及效率的影响,其次对比了SSA 与遗传搜索算法(genetic algorithm,GA)、粒子群算法(particle swarm optimization,PSO)用于SVR 模型优化的效果,然后与其他基于数据驱动的可用容量估算模型进行了对比,最后在不同电池上验证了模型的有效性。
3.1 不同长度训练数据
为探究训练数据量对模型的估计精度及训练速度的影响,分别取电池1 全部老化数据的前50%、60%以及70%数据作为训练集训练模型,对应地,分别将数据的后50%、40%及30%作为测试集,用于验证模型的精度。不同长度训练数据下可用容量估算结果如图8及表2所示。
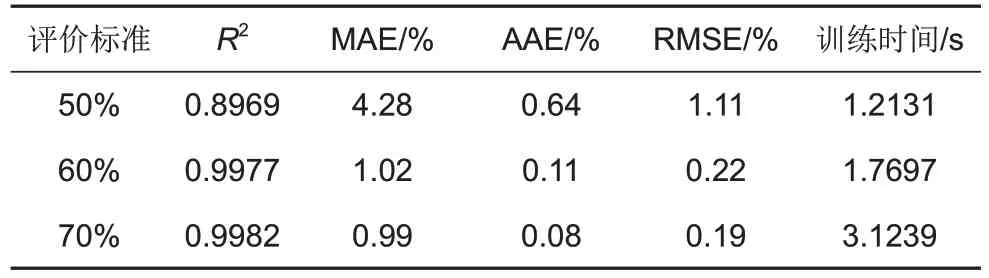
表2 不同长度训练数据估算结果及误差Table 2 Estimation results and errors of different length training data
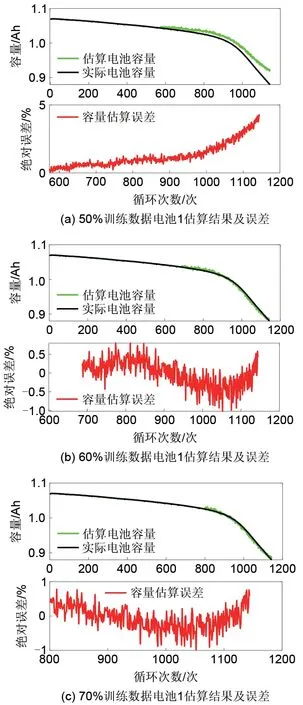
图8 不同长度训练数据估算结果及误差Fig.8 Estimation results and errors of different length training data
由图8和表2可知:①当选择50%的训练数据时,其MAE 达到了4.28%、AAE 达到了0.64%、RMSE达到了1.11%,出现了较大的误差。且随着循环的进行,误差快速增大,表明模型没有很好地学习特征因子与可用容量之间的关系。但由于其训练数据较少,使得模型训练时间最短,仅为1.2131 s。②当选择70%的训练数据时,可用容量估算结果最好,其MAE仅为0.99%,AAE及RMSE分别为0.08%和0.19%,说明模型得到较好地训练,能够很好地跟踪电池可用容量的衰退轨迹。但由于其训练数据较多,导致训练时间最长,达到3.1239 s,为50%训练数据用时的2.6 倍。③当选择60%训练数据时,其MAE、AAE 及RMSE 分别为1.02%、0.11% 和0.22%,模型训练时间为1.7697 s。模型估算精度较高,且估算时间较短,符合电池可用容量准确估计的需求。由于训练数据的增加在提升模型精度的同时也会增加训练的时间,因此综合考虑模型训练时间成本以及模型估算精度情况下,选择60%数据训练模型,并进行后续的模型性能验证。
3.2 不同优化算法
为分析不同优化算法对SVR模型精度的影响,以RMSE最小作为优化目标,将SSA与常用的GA算法以及PSO 算法进行了对比。同时为了体现不同优化算法对比的准确性,将GA、PSO算法参数设置与SSA 参数设置保持一致。估计结果及误差如图9及表3所示。
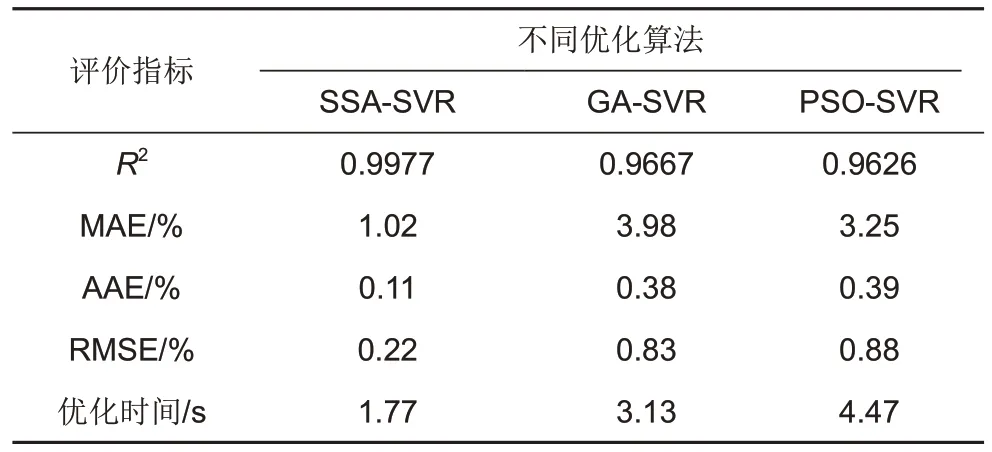
表3 不同优化算法估算结果及误差Table 3 Estimation results and errors of different optimization algorithms
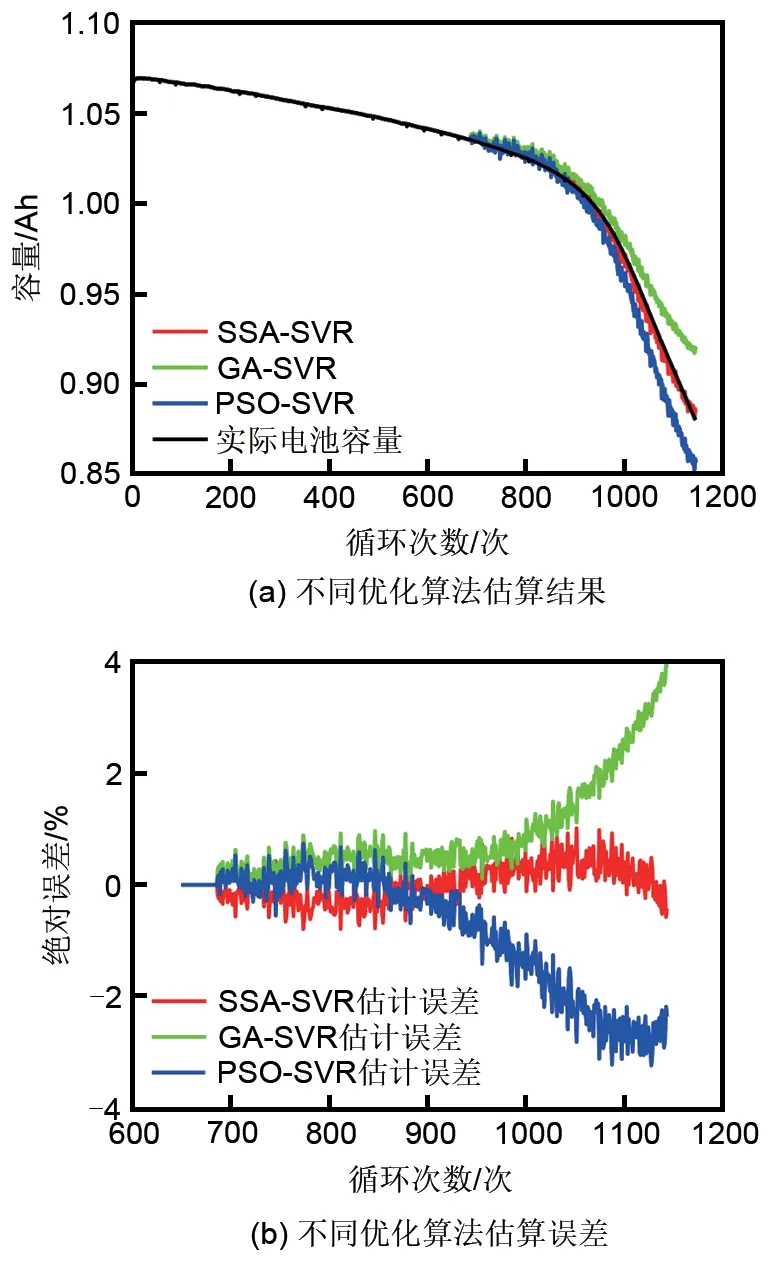
图9 不同优化算法估算结果及误差Fig.9 Estimation results and errors of different optimization algorithms
由图9 及表3 可知:①使用GA 算法与PSO 算法优化的SVR 模型,其可用容量估计结果准确度相近,且明显低于SSA 算法优化的SVR 模型。其中GA 算法的MAE、AAE 及RMSE 分别为3.98%、0.38%以及0.83%,而PSO 算法的MAE、AAE 及RMSE 分别为3.25%、0.39%以及0.88%。模型在电池老化初期能较好地跟踪电池可用容量衰退趋势,但随着循环的进行,特别是当循环达到900次以后,模型估算误差迅速增大。表明GA 算法及PSO 算法在SVR 模型超参数寻优上未能得到较好效果。②利用SSA 算法优化的SVR 模型得到了最好的估算结果,其MAE 仅为1.02%,而AAE 和RMSE 则分别为0.11%和0.22%,表明SSA 算法对SVR 模型的超参数寻优取得了优异的效果,使得模型能够更精确地估计电池可用容量。③在参数寻优耗时上,GA算法及PSO算法分别为3.13 s和4.47 s,而SSA算法用时最短,仅为1.77 s,进一步降低了模型训练的时间,这是因为SSA算法的原理更为简单、参数较少。总之,结果表明,SSA算法具有较高的参数寻优精度且参数寻优速度较快。
3.3 不同数据驱动模型
为进一步验证模型效果,将传统的SVM模型、GPR 神经网络、LSTM 模型与本工作所建立的SSA-SVR 模型进行对比。为保证对比的公平性,四种模型都使用电池1 数据的前60%作为训练集,后40%作为测试集,不同数据驱动模型可用容量估算结果与误差以及几种方法的优缺点如图10 及表4所示。
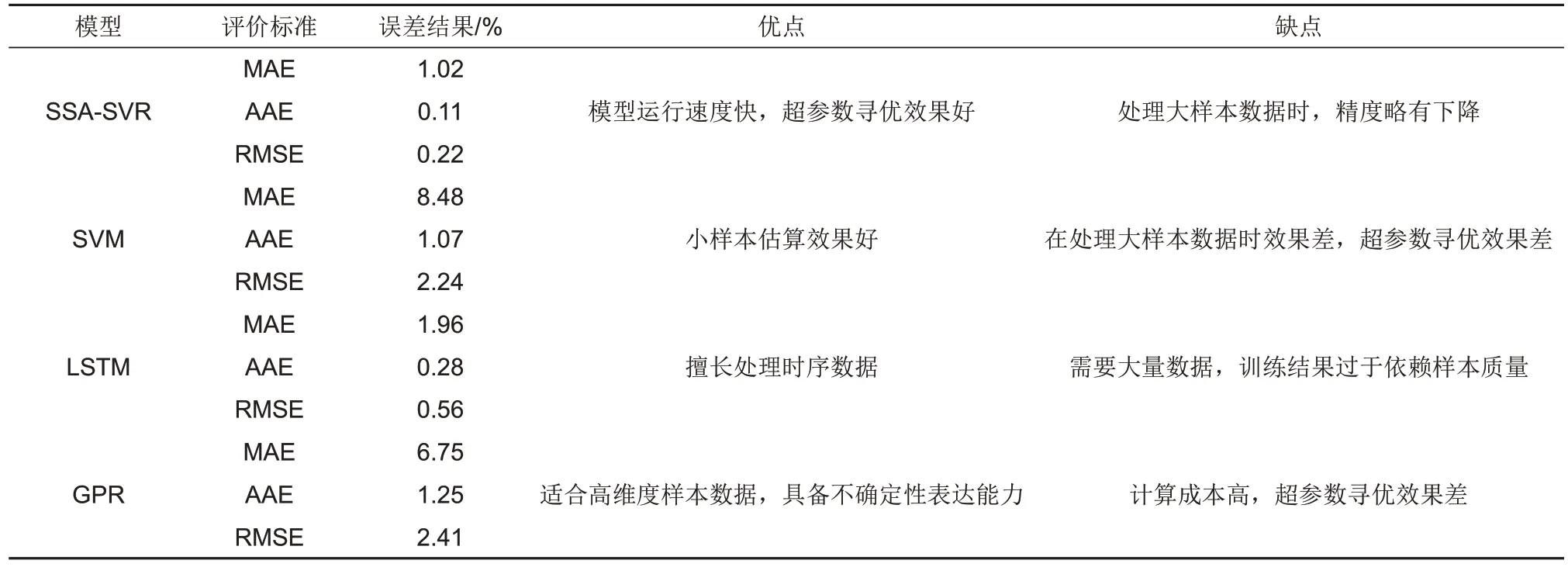
表4 不同方法估算结果及优缺点Table 4 Estimation results and advantages and disadvantages of different methods
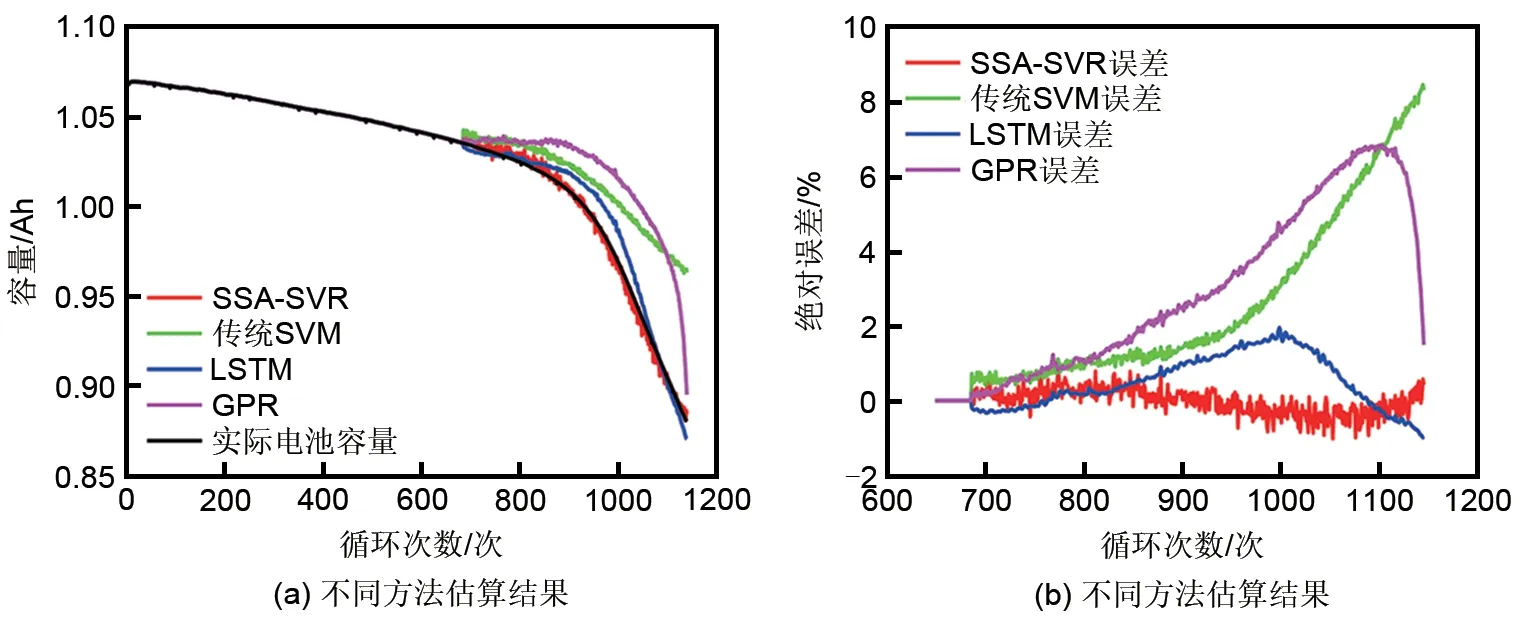
图10 不同方法估算结果及误差Fig.10 Estimation results and errors of different methods
由图10 及表4 可知:①传统SVM 模型在估算小样本数据时效果较好,但随着样本规模的提升,其复杂度会显著提升,同时精度也会有所下降。在本工作中由于其核函数参数寻优效果不理想,未能找到最优的超参数C和g,导致其估算电池可用容量时出现较大的误差,其MAE已经达到了8.48%,是SSA-SVR 模型MAE 的8.3 倍,并且随着循环进行呈现不断增大的趋势。②LSTM模型在长序列数据的训练中有较好的表现,能够较好地估计电池可用容量,其MAE、AAE 及RMSE 分别为1.96%、0.28%以及0.56%,但在可用容量估算的后期,仍出现了大幅偏离容量实际衰退轨迹的情况。③GPR模型能够对不确定性做出可靠的估计,在可用容量估算初期能够较好地估计电池可用容量,但在估算后期同样出现了较大的误差,主要原因还是其本身的共轭梯度超参数寻优方法陷入了局部最优,没能找到最优参数导致的。④SSA-SVR 模型具有最好估算结果,其MAE 仅为1.02%,而AAE 和RMSE则分别为0.11%和0.22%,这表明了SSA 在模型参数寻优上取得了非常好的结果,促使模型能够很好地追踪电池可用容量的衰退过程。综上可知,SSA-SVR 模型具有更好的估算性能,能够准确估计电池的可用容量。
3.4 不同电池
为验证模型在不同电池上的适应性和泛化能力,将电池1的数据作为训练集用来训练模型,将电池2~5的数据作为测试集验证模型的估算精度。可用容量估算结果如图11和表5所示。
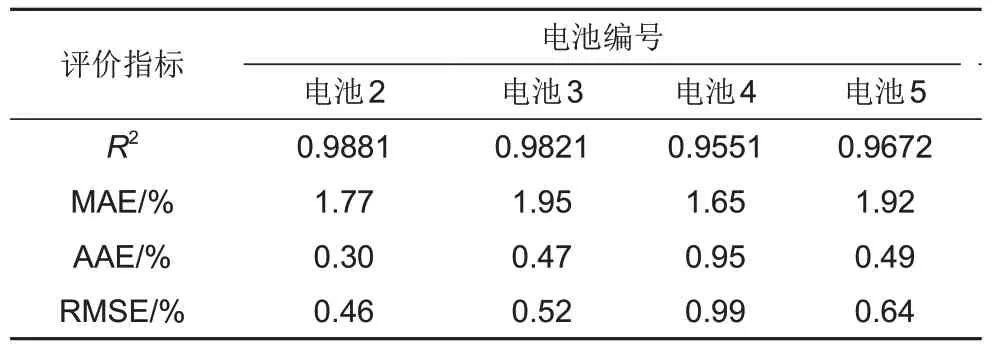
表5 不同电池估算结果及误差Table 5 Estimation results and errors of different batteries
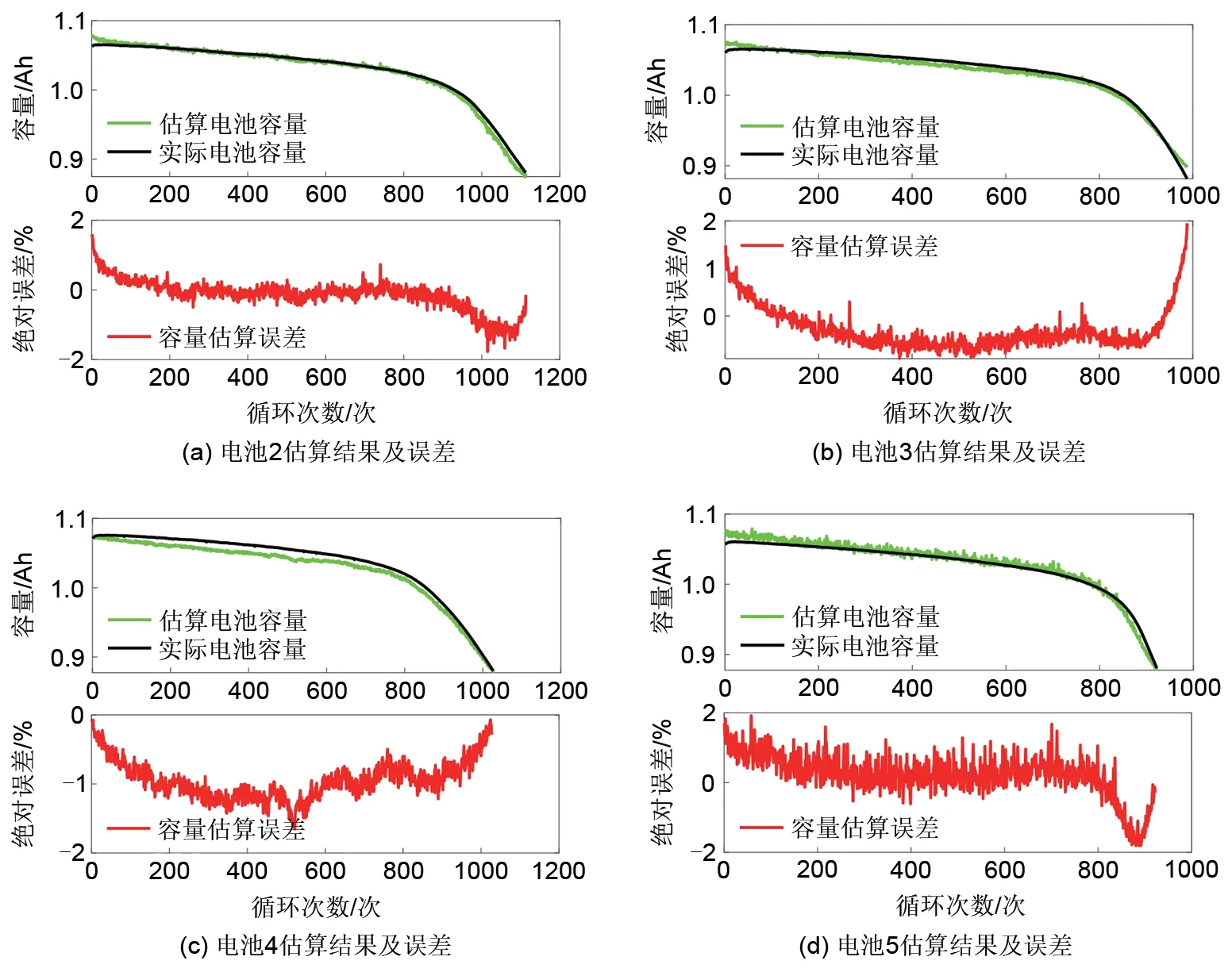
图11 不同电池估算结果及误差Fig.11 Estimation results and errors of different batteries
由图11及表5可知:①电池2~5的MAE分别为1.77%、1.95%、1.65%以及1.92%,最大误差保持在2%以内,且最大误差多出现在可用容量估计的开始和结尾处,整体估算结果较为理想。②电池2 的AAE 及RMSE 分别为0.30%和0.46%,电池3 的AAE 及RMSE 分别为0.47%和0.52%,电池4 的AAE 及RMSE 分别为0.95%和0.99%,电池5 的AAE 及RMSE 分别为0.49%和0.64%,本工作提出的估算模型在不同电池上均表现出了较高的可用容量估算精度。③最大MAE 出现在电池3的可用容量估算中,仅为1.95%,且其AAE 仅为0.47%,估算结果仍较为理想。综上可知,当利用不同电池的数据分别作为训练集和测试集时,模型仍能够准确地估算电池可用容量。
4 结 论
为了解决当前基于数据驱动的锂离子电池可用容量估计算法存在的老化特征提取不准确、可用容量衰退趋势跟踪精度低以及模型参数寻优耗时长等问题,本工作基于SSA-SVR 算法构建了电池可用容量准确估计框架。通过分析电池老化数据,提取了IC 曲线峰值、IC 曲线峰值对应电压2 个特征因子,并通过皮尔逊相关系数分析了所选取特征因子的合理性。然后,基于SVR 算法构建了容量估算框架,针对SVR 本身超参数寻优存在的寻优时间过长、易陷入局部最优、寻优结果不够优良的问题,选用SSA算法进行超参数寻优,完成SSA-SVR模型的搭建;其次,通过不同长度的训练数据下估算结果的对比,确定将全部老化数据的前60%作为训练集;最后与传统的SVM、LSTM 及GPR 进行对比,还在不同的电池上验证了模型的泛化性。结果表明,本工作提出的SSA-SVR 模型具有较高的容量估计精度以及较短的模型训练时间,在不同电池上也有较好的容量估计效果,最大误差为1.95%。
本工作所构建的模型具有精度高,泛化能力强等特点,同时大幅降低了模型训练所用的时间。但目前研究仍停留在准确估计单体电池的可用容量上,在实车情况下实现电池组的可用容量准确估计将是下一步主要的研究方向。

