基于塑性区演化的煤柱宽度留设及柔性锚索支护技术研究

杨永亮，杨 森

（1. 国家能源集团神东煤炭集团公司，陕西 神木 719315；2. 中煤科工西安研究院（集团）有限公司，陕西 西安 710077）

0 引言

合理煤柱宽度设计对巷道稳定性控制、煤炭资源高效回收利用等具有重要意义[1]。不同的煤柱宽度下巷道所处应力环境不同，为了提高巷道稳定性、减小巷道支护难度，通常将巷道布置于开采扰动应力降低区[2-5]。对此，相关研究人员主要通过数值模拟、理论分析、现场探测相结合的方法研究不同工程地质条件下的合理煤柱宽度[6-9]。张金贵等[10]建立了煤柱宽度计算理论模型及数值模型，明确了不同煤柱宽度下的巷道位移场、应力场及塑性区分布特征，并经现场实践进行了验证；王俊峰[11]通过极限平衡理论确定了煤柱宽度为5 m，比原方案多生产原煤2.83万t，有效提高了经济效益；蒋威等[12]认为煤柱稳定性与覆岩结构为巷道变形的主要影响因素，并确定了合理煤柱宽度为5～10 m；何文瑞等[13]基于沿空巷道覆岩结构，揭示了不同煤柱宽度下的巷道应力环境分布特征。在巷道支护方面，针对巷道大变形锚索易过载拉断的问题，李冲等[14]提出采用柔性锚索支护以释放部分能量，经工程实例验证取得了良好的支护效果；曹建来[15]针对五阳煤矿支护密度大、成本高、效果差等问题，提出采用超高强柔性锚杆支护，提高了巷道围岩承载能力，取得了良好的支护效果。

以上研究成果多是针对具体工程地质条件，对布尔台煤矿及类似工程地质条件的矿井应用效果较差。基于此，以神东布尔台煤矿42108辅运巷道为工程实践对象，通过理论分析、数值模拟等方法确定合理煤柱宽度并提出相应支护技术，保障工作面安全高效生产，为类似条件矿井提供借鉴。

1 工程概况

神东布尔台煤矿42煤层平均埋深约350 m，与上覆已采的2号煤层间距为45～78 m，42107工作面位于42煤层一盘区中部，与南侧已开采的42106工作面、北侧未开采的42108工作面之间的区段煤柱均为25 m。42107工作面平均煤厚6.9 m，采用综放工艺进行开采，采高为3.7 m，放煤高度为3.2 m。煤层直接顶是厚度为6.5 m的砂质泥岩，老顶为细砂岩及砂质泥岩；煤层直接底是厚度为6.3 m的砂质泥岩。参考相邻矿井地应力测量结果，该矿井处侧压系数约1.2。工作面综合柱状图及巷道布置示意如图1所示。

图1 地质综合柱状图及巷道布置Fig. 1 Comprehensive of geological histogram and roadway layout

42108工作面辅运巷道设计断面为矩形，宽×高为5.4 m×3.8 m。巷道的原支护方案为：顶板采用“左旋无纵筋螺纹钢锚杆+钢筋网+锚索+π型钢带”，其中，锚杆的规格为Φ22 mm×2000 mm，间排距为1100 mm×1000 mm，锚索的规格为Φ22 mm×8000 mm，间排距为2100 mm×2000 mm，锚索布置在π型钢带上，钢带的规格为4600 mm×140 mm×8 mm；帮部采用“玻璃钢锚杆+木托板＋金属网”，其中，锚杆的规格为Φ18 mm×2000 mm，间排距为800 mm×1000 mm，金属网的规格为1200 mm×4200 mm，网孔的规格为45 mm×45 mm。42108工作面辅运巷开掘并进行支护后，在42107工作面采动的影响下出现了帮部移近量接近1 m的大变形，进行多次补强支护后仍然不能有效地控制巷道变形。辅运巷表面变形量及深基点变形量实测情况如图2所示，均为该测站首次测量时与工作面的距离。

图2 巷道变形量实测Fig. 2 Actual measurement of roadway deformation

2 回采巷道塑性区演化特征

2.1 巷道塑性区分布特征

王卫军等[16]给出了非等压圆形巷道围岩塑性区分布形态隐性方程，见式（1）。

式中：γ为岩石容重，取25 kN/m3；H为埋深，取350 m；k为侧压系数，取1.2；R为当量巷道半径，计算得R=3.3 m；r、θ分别为极坐标任一点半径及角度；c为黏聚力，取7 MPa；φ为内摩擦角，取41°。

将42108辅运巷相关参数带入式（1），当f（r，θ）=0时可得巷道围岩塑性区分布方程，如图3所示。由图3可知，侧压系数不同时巷道塑性区分布形态不同。整体上，巷道塑性区形态向右偏转约20°，说明42107工作面开采时42108辅运巷发生了应力向右偏转约20°。塑性区分布范围随侧压系数的增大而增大，在巷道所处应力环境中（k=1.2）塑性区分布范围为1.8～2.7 m，呈现非对称破坏特征。

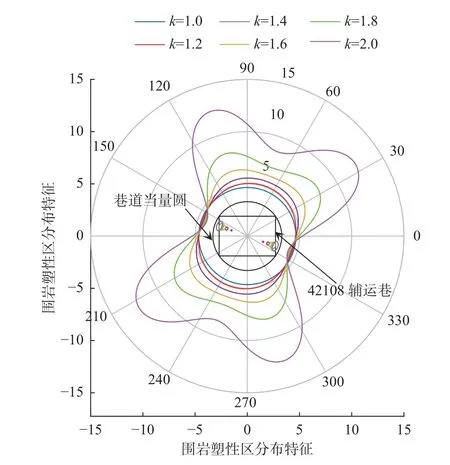
图3 42108辅运巷塑性区分布规律Fig. 3 Distribution law of plastic zone in 42108 auxiliary haulage roadway

2.2 煤柱宽度的塑性理论计算

为确定合理煤柱宽度，降低巷道维护难度，以42108辅运巷为例，采用极限平衡理论初步计算合理煤柱宽度。沿空巷道的保护煤柱宽度通常可分为三部分（图4），其中X1为沿空巷道锚固有效长度，X2为根据工程地质条件增加的保障性安全系数区，X3为区段煤柱受相邻工作面采动采动影响产生的塑性区宽度，按X2=0.3（X1+X3）计算，则煤柱宽度B=X1+X2+X3。

图4 煤柱的弹塑性变形区Fig. 4 Elastic-plastic deformation zone of coal pillar

根据极限平衡理论[17-18]，采动塑性区宽度X3可表示为式（2）。

式中：M为采高，取3.2 m；ξ为三轴应力系数，ξ=（1+sinφ）/（1-sinφ）；f为煤层与顶底板的摩擦系数，取0.2；k1为应力集中系数，取3；P1为支护结构对煤体的支护强度，取0.1 MPa。将上述各参数带入式（2），得X3=9.48 m。

巷道掘进形成的塑性区宽度X1可表示为式（3）。

式中：α、k2为广义Mises准则系数，α=

将上述参数带入式（2），得X1=10.90 m，则X2=6.11 m，煤柱宽度B=26.49 m。即通过极限平衡理论可得，煤柱宽度应不小于26.49 m。

2.3 不同煤柱宽度巷道塑性区分布形态

基于42108辅运巷工程地质条件建立FLAC3D数值模型，明确巷道塑性区分布特征。数值模型长×宽×高为1000 m×600 m×200 m，包含2#煤层、4#煤层等在内共12层岩层，各岩层物理力学参数见表1。模型左右两侧各留50 m保护煤柱，固定模型前后左右及底部边界，在模型顶部施加8.25 MPa垂直载荷模拟覆岩应力。42煤层上覆45～78 m为22煤层采空区，因此采用双屈服模型描述22煤层采空区垮落岩体的破坏特征，其他岩层的破坏准则为Mohr-Coulomb准则。

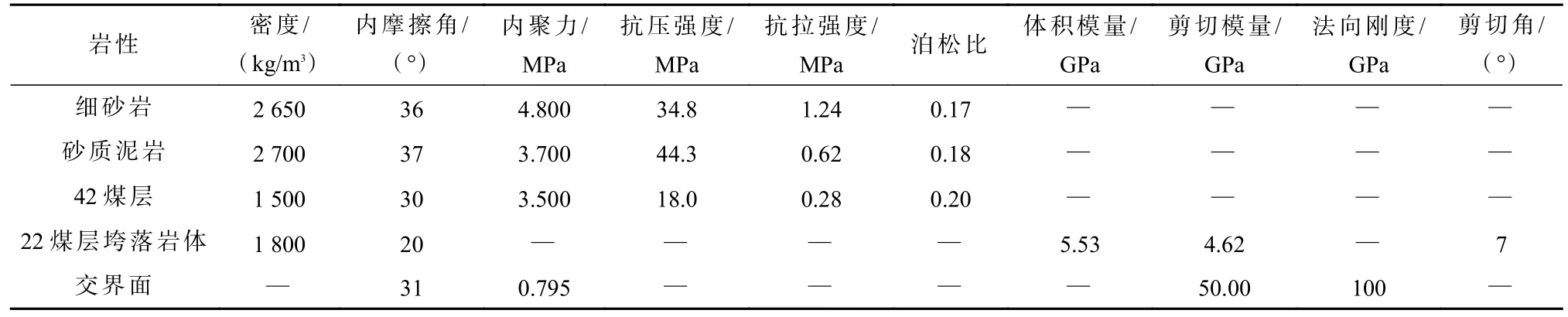
表1 岩石力学参数Table 1 Rock mechanical parameters

双屈服模型参数校核过程为：通过经验公式确定22煤层垮落带发育高度为12 m，通过Salamon经验公式确定垮落岩体理论应力-应变关系，最终采用试错法比对数值模型中的块体应力应变关系与Salamon理论计算结果，一致性极高时即可将该参数作为双屈服模型的参数，结果见表1。

细化巷道附近区域的网格密度以提高计算精度，同时保障计算速度。按上述方案进行模拟，不同煤柱宽度下的塑性区分布形态如图5所示。由图5和图6可知，不同煤柱宽度下巷道塑性区均呈非对称分布形态，煤柱宽度为25 m时顶板塑性区达3.5 m，煤柱侧塑性区3.5 m，煤壁侧塑性区3 m且与顶板非对称塑性区贯通，底板塑性区非对称性与顶板相反，这与理论分析所得结果一致；煤柱内部有两个距离较近的弹性核，此时巷道处于应力集中区与卸压区的交界处，在一定程度上仍影响巷道稳定性。煤柱宽度为30 m时，煤柱侧塑性区范围减小为3.0 m，但煤柱内部两个弹性核中间出现明显的应力降低区，这有利于降低巷道维护难度，增强巷道稳定性。随着煤柱宽度的继续增大，巷道塑性区发育范围基本未变，随之变化的是两个应力弹性核区的间距，但这表明此煤柱宽度下巷道已处于卸压区。综上所述，考虑塑性区发育范围、应力分布特征及煤炭回收率，确定煤柱宽度为30 m。

图5 不同煤柱宽度下的塑性区分布形态Fig. 5 Distribution pattern of plastic zone under different pillar widths

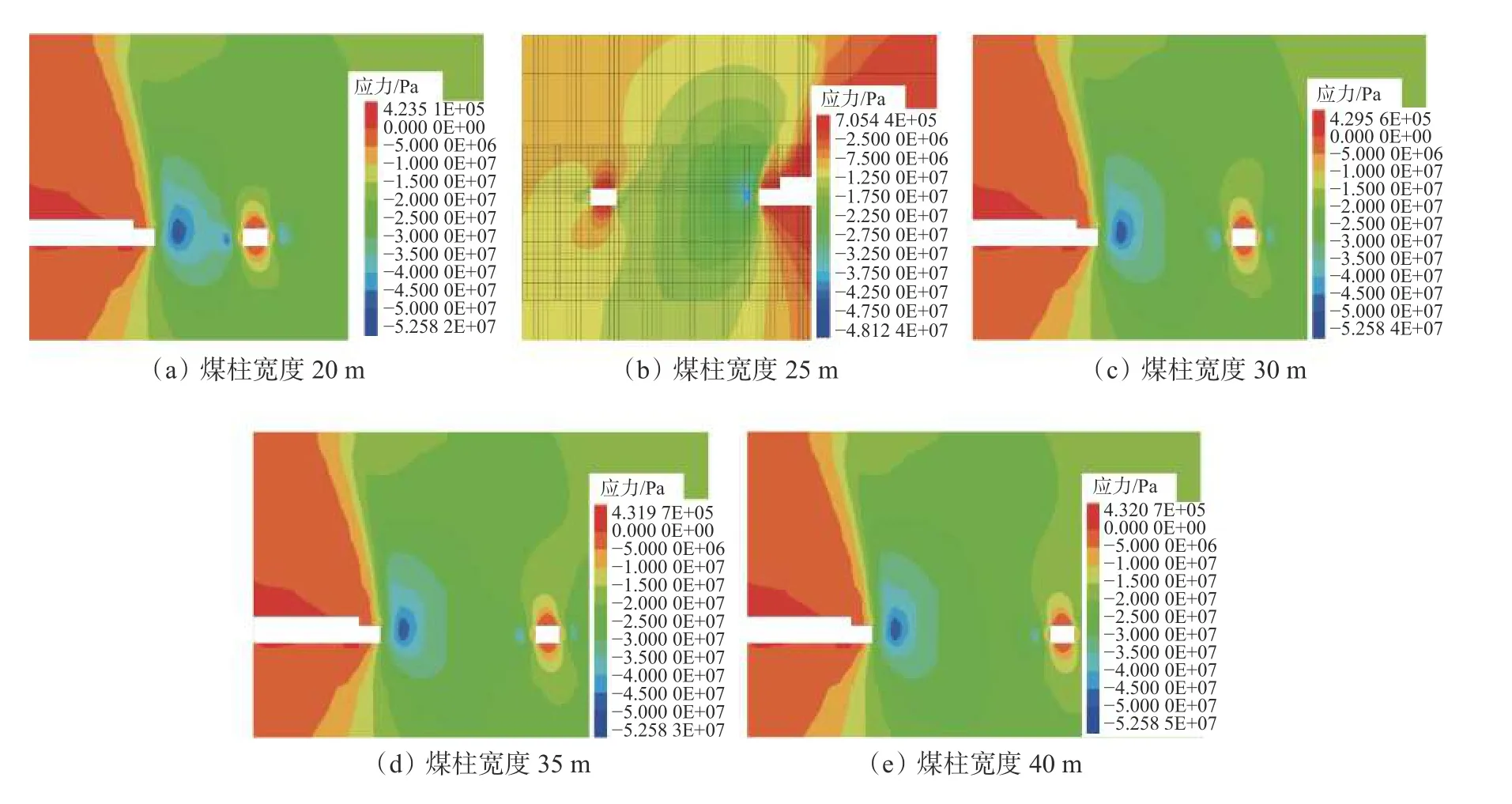
图6 不同煤柱宽度下的垂直应力分布特征Fig. 6 Vertical stress distribution characteristics under different pillar widths

3 柔性锚索支护技术研究及应用

3.1 巷道大变形失稳原因

结合前文所述，巷道进行了多次补强支护仍无法有效控制巷道变形量，模拟分析了煤柱宽度为25 m时不同锚索支护方案下的巷道塑性区分布特征，揭示巷道大变形失稳原因，为30 m煤柱宽度下的巷道支护方案设计提供借鉴。支护方案主要为补强支护，模拟结果如图7所示。由图7可知，不同支护方案下巷道塑性区形态均呈蝶形分布，与图3所示理论分析结果较为一致。经计算，顶板补强支护3根锚索、6根锚索、9根锚索时，支护阻力分别为0.52 MPa、0.72 MPa、0.91 MPa，此时图7（c）所示的顶板塑性区最大深度减小至3.2 m，相比原支护方案仅减小0.3 m，塑性区面积由原支护方案下的14.92 m2减小到13.28 m2，3种补强支护方案对顶板塑性区面积控制率分别为9.00%、12.25%、17.00%，塑性区依然呈现非对称形态。

图7 补强支护下巷道塑性区分布Fig. 7 Distribution of plastic zone in roadway under reinforcement support

综上所述，提高支护阻力对控制巷道围岩破坏范围的作用较为有限。锚杆锚索支护作用的实质是将塑性变形围岩锚固在稳定岩层中，形成组合梁、加固拱等结构增强浅部围岩承载能力，从而控制巷道非连续大变形，而42108辅运巷整体变形量较大，帮部锚索呈现拉伸破断形态，这意味着现用锚索无法有效适用于该巷道，据此提出采用延伸率较大的柔性锚索进行高强让压支护。

3.2 柔性锚索补强支护方案

柔性锚索内部充填了一定量的橡胶块，当巷道发生大变形锚索内钢绞线受力超过某一阈值时，橡胶块受压逐渐开始变形，将锚索内部钢绞线拉直，达到既增大锚索延伸率的同时又不损害锚索整体强度的目的。

柔性锚索由7股高强度低松弛的钢绞线组成，杆体直径22 mm。在杆体上每隔0.5 m设置一个鸟巢结构填充橡胶块，填充长度为0.1 m，单个鸟巢可伸长2～3 cm，锚索整体延伸率可达20%，相比普通锚索延伸率约为4%。

在现有支护方案的基础上，将帮部锚杆间距缩减至750 mm×750 mm，并增加三根柔性锚索进行补强支护，锚索规格为Φ22 mm×6500 mm，间排距1500 mm×1500 mm；同时将顶板的锚索规格更换为Φ28.6 mm×8000 mm，间排距不变，支护方案示意如图8所示。

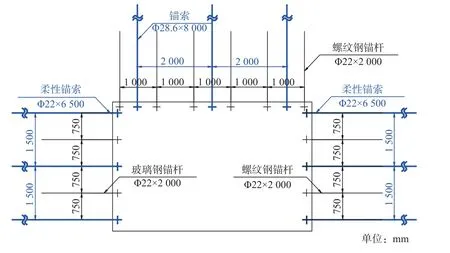
图8 支护方案Fig. 8 Support scheme

3.3 工业性实践

按上述支护方案进行施工并持续监测巷道帮部移近量，结果如图9所示。其中，进行首次测量时测站1、测站4的位置分别超前工作面30 m、80 m，测站2、测站3分别滞后工作面40 m、20 m。由图9可知，巷道施工后两帮位移量显著降低，受采动影响时间较短的区段30 d时巷道位移量为40～80 mm，受采动影响时间较长的区段（如原帮部位移量约1 m的区段）此时仍产生160 mm左右的片帮量，但整体控制效果显著，为巷道安全高效开采提供了有力保障。

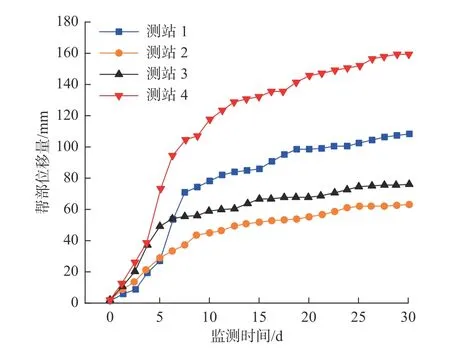
图9 巷道支护效果Fig. 9 Roadway support effect

4 结论

1）明确了巷道塑性区非对称蝶形向右偏转约20°分布的形态，塑性区分布范围为1.8～2.7 m。

2）建立了煤柱弹塑性力学模型，基于极限平衡理论明确了合理煤柱宽度应不小于26.49 m，结合数值模拟进一步明确了不同煤柱下的塑性区及应力场分布特征，综合考虑确定了合理煤柱宽度为30 m。

3）结合数值模拟明确了多次补强支护仍无法有效控制巷道变形量的原因，在此基础上提出了柔性锚索支护方案，经现场实践后30 d内两帮最大变形量160 mm，围岩控制效果显著。