利用计算机数值模拟探究悬链线的形状
杨一鸣 刘博文 石 磊
(1. 南京师范大学附属中学,江苏 南京 210000; 2. 复旦大学物理学系,上海 200433)
《抱银貂的女人》是达·芬奇所画的世界名画.在创作此画的过程中,如何写实地描绘画中主人公脖颈上所戴的一串黑色珍珠项链,让达·芬奇陷入了沉思:固定项链的两端,使其在重力的作用下自然下垂,项链所形成的曲线应该是什么?在高中阶段学习了力学和曲线方程的情况下,高中学生可能对这个问题感到好奇,但因为缺乏微积分知识,无法进一步探究.
计算机在当今科学研究中起到重要作用,利用计算机辅助解决问题的思路也有很大价值.尽早让高中生提前接触这类思想可以帮助他们自主探究一些原本在高中阶段难以讨论的问题,拓展思维宽度,益处良多.[1]在本文中,我们将主要介绍如何利用计算机数值计算,处理原本需要高阶变分数学技巧才能解决的悬链线问题.在此过程中,我们还将介绍与悬链线问题相关的最小作用量原理和最小势能原理.这将有助于高中生开阔视野,理解书本上的物理知识背后的图像和原理,形成一种完整统一的物理观.
1 最小作用量原理、最小势能原理
物理学家们有一个信念:“大自然不会做徒劳无功的事情(Nature does nothing in vain).”即一切物理现象的发生一定是因为这样发生最为“省劲”,大自然倾向于以“作用量”最小的方式运行,这就是“最小作用量原理”.[2]
物理学家们始终在探讨何为“作用量”.不同的科学家提出了各种不同的“作用量”.费马提出“最短时间原理”,即光线移动的路径是用时最少的路径.莫佩尔蒂提出作用量为质量和速率的积在运动路径上的积分.哈密顿提出作用量为动能与势能的差在运动时空上的积分等.而针对静力学问题,伯努利提出了“最小势能原理”:当一个体系处于稳定平衡状态时,其系统的势能最小.本文将依据此原理进行探讨.
2 悬链线问题
悬链线问题是一个非常古老的问题,伽利略认为是抛物线但并未证实,达·芬奇提出问题后还没有找到问题的答案便去世了,最终伯努利利用最小势能原理解决了悬链线问题.[3]悬链线问题的具体描述是:两端固定的一条均匀(粗细与质量分布)、柔软(不能伸长)的链条,在重力的作用下所具有的曲线形状.在本文中,不考虑绳子的弹性势能,仅仅考虑重力势能.在实际的教学探索中,也可以鼓励学生自主探究考虑弹性势能的情况.本质上,从最小势能原理出发,悬链线问题是一个数学上的变分问题,在高中阶段原本是难以讨论处理的.但事实上,高中生可以借助计算机数值计算,在避开微积分的情况下,将积分问题转化为求和问题,直接计算机模拟得到悬链线问题的近似解.
如图1,将悬链线分成很多小段,设每一小段水平长度为Δx,竖直长度为Δy,坐标为(x,y),绳子密度为ρ=ml,并且其数值被设定为1.则对于每一小段,它的长度为
(1)
这一小段质量为
(2)
因此该小段的势能ΔV为
(3)
将每一小段的势能累加求和,便得到整个悬链线的总势能,为
(4)
根据最小势能原理,悬链线应是总势能取最小值时的曲线.对于这样一个求和问题,学生可以借助于计算机很容易地实现.同时,也能够利用交互式的界面,通过改变曲线的形状,直观地感受不同形状对应的势能大小,以及符合最小势能情况下的悬链线曲线.
具体而言,学生可以在计算机显示屏上生成一个交互式界面,界面中创建许多滑动条,每一个滑动条对应于悬链线上的一个点,而两点之间的横纵坐标差即是Δx和Δy,并利用式(4)实时计算出总势能并显示在屏幕上.通过调整曲线形状、观察势能值,就可以认识到悬链线的形状以及深刻理解最小势能原理.
3 使用计算机数值模拟悬链线形状
下面介绍具体的代码实现过程.本文以mathematica为例,其他的程序语言,例如python等均可完成任务.
定义悬链线的两固定端的坐标为(-1,0)和(1,0),从-1到1每0.2取一个点.该点的横坐标和纵坐标在程序中分别为x和y.这里,为了方便起见,没有赋予数字的具体单位.教师可以根据实际需要定义.首先,利用公式(4)计算总势能的程序为:

为了更加直观,也增加程序与学生的交互性,如前所述,我们可以制作交互式界面,通过滑动条控制构成悬链线上的点,进而调节悬链线形状.通过在屏幕上实时显示曲线形状和所计算的总势能,体现形状和势能的关系.具体可以利用mathematica中的ListLinePlot函数和manipulate函数实现.具体程序实现如下:

值得注意的是,确保探究正确的基本条件是保证总绳长不变.如果直接从-1到1设立多个滑动条会导致总绳长受到影响,进而影响结果.一种解决方法是,空出中间横坐标为0的点,自动改变它的位置以保证总长不变.设它左右两侧点的纵坐标为y1,y2,当前总长度与总长度的差值为Δl,得到方程
(5)
只要解出方程(5),即可得到此时中间点的纵坐标,以保证总长度l相同.可以用如下语句解出方程,并将输出作为函数calcmid的定义(程序中的y/.可以将Solve函数的输出中的y替代为calcmid):

然后我们可以定义len函数来计算y1和y2,并利用它计算中间坐标.

定义好函数后,可以按如下方式计算中间点的坐标:

为了方便,在实际的编程中,教师可以预先利用已知的悬链线曲线获得悬链线的总长度l.最终的程序交互式界面如图2所示.运行程序后,在调整图像形状的同时,界面上可以直接显示总势能的变化.可以看出,当曲线逐渐接近悬链线时,总势能也在不断减小.最终得到的曲线即为近似的悬链线.

图2
图2为最小势能模拟计算机界面.左侧的滑动条分别对应着右侧图中点的纵坐标,可以通过拖动滑动条改变点的位置。右图会显示出所有点的位置,并计算出此时对应的势能。(假设,横纵坐标单位为m)
4 做实验进行验证
为了验证在实际生活中很多固定两端的悬链线的形状的确是符合最小势能原理,可以使用珍珠项链等进行简单实验.以珍珠项链为例,测量出项链长度后,控制两端点间的距离为15 cm和20 cm,将程序中l设为总长与短点距离比值的两倍(因为程序中将两端点距离设为2).观察项链形状,并与拟合出的形状进行比较.可以发现曲线是几乎重合的(如图3),因此可以认为得到的悬链线曲线的确是最小势能情况.也可以让学生运用相同方法自主探究两端点不等高的情形,拓展思维.
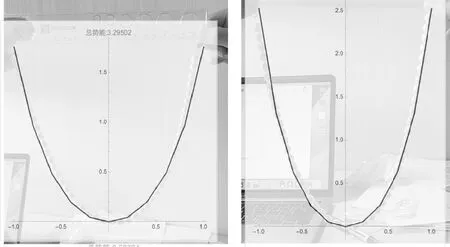
图3
图3将珍珠项链两端点距离控制为15 cm和20 cm,并输入到程序中,模拟出势能最小时的曲线,并与原图进行对比.图像坐标轴单位为任意单位.
5 与抛物线的区别
悬链线和抛物线看起来非常相似,相信有很多学生会猜测悬链线曲线形状实际上就是抛物线.但是我们通过程序模拟,可以排除掉悬链线是抛物线的可能性.
如图4,先通过上述方法调整出悬链线图案(实线),然后分别作出过曲线两端点和极值点(A、B、C3点)的抛物线(虚线).因为3点可以确定一个这样的抛物线,如果悬链线曲线为抛物线,实线和虚线形状应相近.然而可以发现悬链线长度与两端点距离的比值越大(悬链线竖直方向上越长),它的图像和抛物线差异越大,因此可以排除悬链线为抛物线的可能性.

图4
6 生活中的悬链线
进一步,还可以组织学生寻找生活中的悬链线并进行自主探索.例如,找到生活中的悬链线并拍照.通过测量估算出大致绳长后,输入到程序中,通过拖动各个节点找到最小势能曲线,再将曲线与实际情况进行比较.
例如,图5是一张常见的河边石墩间铁链的照片.设两端点距离数值为2,则可以用棉线测出它的对应的长度数值约为17/8.将程序中的长度数值设为17/8,再不断拖动点,达到势能最小时,观察线的形状.最终可以发现与图片中悬链线形状相似.

图5
7 结语
本文主要介绍如何通过计算机模拟的方式,结合最小作用量原理在高中教学中探讨悬链线问题.利用计算机数值计算的强大能力,将积分转变为求和,并借助交互式界面这样一个有趣的方式,弥补高中生现阶段数学知识的不足,使高中生对悬链线问题和最小作用量原理有较为直观的理解.
更为重要的是,本论文的尝试说明了利用计算机模拟的思路在高中学习中将会起到重要作用.鼓励高中学生在遇到无法凭借自己现有知识解决的问题时,运用信息技术,通过计算机模拟的方式得到近似结果,将有助于学生创新素养的培养.
本文受到复旦大学“步青计划学术见习课程:物理学中的作用量”课程的支持.
——《势能》

