ZIF-8多孔材料吸附CO2的格子Boltzmann模拟

杨会盼, 金 晶, 赵 健, 侯封校, 丁正浩, 朱 杰

(1.上海理工大学 能源与动力工程学院,上海 200093;2.中钢集团鞍山热能研究院有限公司,辽宁鞍山 114000;3.中北大学 能源与动力工程学院,太原 030051)

目前,我国能源消费仍以煤炭、石油和天然气等化石燃料为主。但化石能源在转化与利用过程中会排放大量CO2,引起全球气候反常等环境问题。因此,基于我国能源消费情况以及国家“双碳”计划的战略形势,对传统化石能源的使用必将向无污染、低碳乃至“零碳”技术方向转型。二氧化碳捕集、利用与封存技术是针对化石能源碳排放和环境改善的一种综合性解决方案[1]。CO2吸附分离法是目前研究及应用最多的燃烧后CO2捕集技术之一[2]。

沸石咪唑酯骨架(Zeolitic Imidazolate Frameworks,ZIFs)系列材料[3-4]是一种由过渡金属和咪唑衍生物配体合成的新型金属有机骨架吸附材料,具有选择性好、吸附量大的特点,是一类有潜力的CO2吸附材料。ZIF-8材料作为ZIFs系列材料的典型代表,由于其优异的热稳定性和化学稳定性以及在CO2气体储存和分离方面显示出的巨大潜力,受到国内外学者的广泛关注[5-6]。Zhang等[7]在ZIF-8材料骨架中加入了烷基胺,以增加ZIF-8表面碱基数量,提高其对CO2的吸附能力和选择性。Liu等[8]研究了ZIF-8与氨基修饰后的ZIF-8-NH2和ZIF-8-(NH2)2对CO2的吸附效果,结果显示适当的氨基官能化可直接增强ZIF-8对CO2的吸附量。Vendite等[9]研究了ZIF-8材料表面成分对CO2选择性的影响,结果发现N2分子的存在几乎不影响CO2的吸附,且ZIF-8颗粒表面富含不饱和锌原子的纳米颗粒时,CO2捕获量会大大增加。

目前,针对ZIF-8吸附材料的研究工作集中在通过增加ZIF-8材料的表面修饰来提高其对CO2的吸附效果,而针对ZIF-8颗粒本身的不同多孔形态对CO2动态吸附性能产生影响的研究缺少相关报道。格子玻尔兹曼方法(Lattice Boltzmann Method,LBM)是一种不依赖于连续性假设的介观尺度数值模拟方法,具有易于处理复杂边界的优点[10-11]。经过几十年的发展,现已有许多学者利用LBM研究了多孔介质内非均相反应流动等问题。刘波等[12]、Wang等[13]采用LBM分别对单颗粒多孔MgO、铜-苯-1,3,5-三羧基颗粒吸附CO2过程进行了数值模拟,讨论分析了不同孔隙率和粒径对吸附效果的影响。

笔者采用LBM模拟研究ZIF-8多孔材料吸附CO2的过程,研究其内部流动与吸附扩散过程,对ZIF-8吸附剂颗粒的孔隙率、排列方式以及粒径如何影响CO2吸附过程进行了分析,目的是获取ZIF-8吸附CO2体系的微观信息,指导设计合成出高效且低成本的ZIF-8材料,用于CO2混合气体的选择性吸附存储。

1 物理模型

图1所示为ZIF-8多孔材料吸附CO2的物理模型,尺寸为2 mm×3 mm。吸附管道为圆柱体,整个系统呈轴对称,可将计算域简化为二维模型。在二维管道内填充有圆形ZIF-8吸附剂颗粒,左右管壁为绝热不可渗透边界,从燃煤电厂出来的烟气经过脱硫脱硝工艺后以0.002 m/s的流速通入ZIF-8吸附床中。模拟烟气浓度为5.9 mol/m3,组分为体积分数14.5%的 CO2和体积分数85.5%的 N2。为使反应更加充分,烟气从吸附床下端入口流向上端出口,CO2吸附发生在ZIF-8吸附剂颗粒填充的吸附床上。区域内温度保持恒定308 K,忽略吸附过程造成的温度变化。

在LBM中,数值计算的精度、稳定性以及效率受边界条件影响很大[14]。经过网格无关性验证后,计算域的网格数取200×300,吸附区域取中间200×200,上下各留出200×50个格子。在初始时刻,整个区域内CO2浓度与速度数值均为0。吸附床下端入口处密度、速度及浓度恒定,在吸附床内混合烟气流动达到充分发展,上端出口速度不再变化,组分场在出口处均为零梯度边界条件;左、右侧管道壁面处的速度场采用无滑移边界条件,组分场为零梯度边界条件。

在众多研究结果基础上[4,15],建立3组共11种不同工况,参数见表1。

2 格子Boltzmann模型

2.1 流动场模型

采用Guo等[16]提出的表征体元(Representative Elementary Volume,REV)尺度下渗流广义LBM模型模拟ZIF-8多孔材料吸附CO2的气体流动过程,采用D2Q9模型,在二维空间内有9个离散速度。其演化方程为:

(1)

式中:fi(x,t)为t时刻x处的速度为ei的粒子密度分布函数;c为格子速度,c=δx/δt,δx为格子步长,δt为时间步长,本文c取1.0;ei为粒子离散速度,对于D2Q9,e0=(0,0),e1=-e3=(1,0)c,e2=-e4=(0,1)c,e5=-e7=(1,1)c,e6=-e8=(1,-1)c;τυ为与流体运动黏度υ相关的流动格子方程无量纲松弛时间。

(2)

外力项Fi定义为:

(3)

F的表达式为:

(4)

式中:G为体积力;K为多孔介质的渗透率;Fε为多孔介质的结构参数。

(5)

(6)

式中:d为固体颗粒的直径。

与标准LBM模型类似,渗流密度ρ和速度U定义为:

ρ=∑fi

(7)

(8)

(9)

式中:a0、a1为参数;v为一个临时速度。

(10)

(11)

(12)

对格子Boltzmann方程(1)进行Chapman-Enskog多尺度展开,即可得到N-S方程:

(13)

∇(εp)+F

(14)

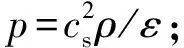
2.2 组分场模型

REV尺度的多孔介质吸附过程可以通过混合气的连续性方程和动量方程描述流场,而通过引入一个被吸附气的浓度扩散方程来描述微量气体的吸附过程[17]。采用Agarwal等[18]提出的D2Q5多孔介质吸附模型模拟ZIF-8多孔吸附材料的吸附过程。其演化方程为:

(15)

式中:gi(x,t)为t时刻x处的速度为ei的粒子浓度分布函数;对于D2Q5,e0=(0,0),e1=-e3=(1,0)c,e2=-e4=(0,1)c;τc为与扩散系数D有关的浓度格子方程的无量纲松弛时间。

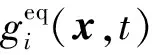
(16)

式中:对于D2Q5,ω0=1/3,ω1～ω4=1/6;a为吸附常数;m为吸附等温线的斜率。

(2)民俗风情生态游。张家界属于民族地区，生活在此的民族主要有土家族、白族、苗族。但是与相邻近的湘西州、恩施州相比较，民族人口密度不高、民族资源不算丰富。因此对于此类偏弱势的旅游资源，不能按照民族聚居地区的开发模式进行生搬硬套，这样开发出来的产品不具备市场竞争力。将民俗风情融入到景区开发中，是一个比较合适的选择。比如，在景区基础设施的建设中，可以把土家族、白族、苗族的民族元素展示到建筑设施中，这样既美观又实用；在景区周边开设剧场，进行民俗歌舞演艺，生动地向游客展示民俗风情；邀请专家设计具有民族特色的旅游商品，要注重产品的高品味，避免随市场的大流。

宏观浓度定义为:

ε+amC=∑gi

(17)

气固之间的吸附平衡受到多孔介质中气体迁移所带来的局部波动的影响。采用Langmuir吸附速率方程来揭示ZIF-8多孔材料中CO2气体的吸附特性[19]:

(18)

式中:V为吸附量;Vm为饱和吸附量;ka为吸附速率常数;kb为脱附速率常数。

3 流动耦合传质模型的验证

为了验证流动耦合传质模型的正确性,对在二维管道内充满了多孔介质的泊肃叶流动及传质扩散过程进行模拟。假设计算域大小为100×100,入口处有一固定速度U0,参数设定为:ε=0.5,Re=33.3。其流动宏观控制方程为:

(19)

解析解为

(20)

(21)

其中,γ=υε/(Kυe);H为沿Y轴方向的高度。

在入口处设置恒定的浓度c0,计算域内其他处的初始浓度设为0,吸附速率常数为0.05,脱附速率常数为0.01[20]。

图2(a)为出口处沿Y方向速度的分布曲线,其中H为沿Y轴方向的高度。由图2(a)可以看出,采用LBM获得的模拟值与方程解比较吻合。图2(b)给出了出口处吸附量和浓度的关系。由图2(b)可知,模拟值与Langmuir等温曲线拟合良好。图2的拟合结果证明了该模型的正确性。

4 数值研究结果与讨论

4.1 吸附剂粒径的影响

图3给出了时间步长为300 000时不同ZIF-8吸附剂粒径下的气体流速分布、CO2浓度分布和颗粒内吸附量分布。通过对比图3(a)的速度云图可知,在颗粒分布较稀疏区域,流场速度均出现明显增大。这是由于气体在吸附剂颗粒较密集区域受到更大的阻力,使更多气体流向稀疏区域。且粒径越大,颗粒分布越不均匀,局部速度增大越明显。

(a) 速度

ZIF-8颗粒吸附CO2过程的质量扩散阻力分为两部分:粒子间对流扩散阻力和粒子内扩散吸附阻力。由图3(b)和图3(c)可以看出,随着粒径的增大,CO2浓度扩散的区域增大,颗粒吸附量也增大。这是由于相同孔隙率的颗粒内传质阻力相等,但粒径越大,稀疏区域的局部对流作用变强,导致颗粒间传质阻力减小。因此,在计算范围内吸附床中CO2质量扩散速率和吸附速率均随着ZIF-8吸附剂粒径的增大而增大。

图4给出了出口处不同吸附剂粒径下的流场速度、颗粒内CO2浓度随时间的变化。由图3和图4可知,在吸附初始阶段,速度场很快就达到流动稳定状态。随着吸附的进行,颗粒内CO2浓度逐渐增大,且增大速率逐渐变慢。粒径为0.05 mm时,吸附床中流场区域的局部速度为0.000 54 m/s,CO2浓度为4.14 mol/m3;粒径为0.20 mm时,吸附床中流场区域的局部速度达到0.000 72 m/s,CO2浓度为5.46 mol/m3,这证实了前文中所说粒径越大,局部速度增大越明显,ZIF-8颗粒吸附CO2越多的观点。

图5给出了不同粒径下ZIF-8吸附剂对CO2的吸附量随时间的变化。由图5可知,随着ZIF-8吸附剂对CO2的不断吸附,颗粒内部的吸附位点不断被消耗,剩余固体量越来越少,导致吸附量曲线斜率均越来越小,即吸附速率逐渐减小。随着粒径的增大,达到吸附平衡所需时间逐渐缩短。

4.2 吸附剂孔隙率的影响

图6给出了时间步长为300 000时不同ZIF-8吸附剂孔隙率下的气体流速分布、CO2浓度分布和颗粒内吸附量分布。对比图6(a)速度云图可知,吸附剂孔隙率越小,局部流速增大越明显;吸附剂孔隙率越大,吸附区域速度分布更为均匀。这是由于孔隙率越小,颗粒内部流动阻力越大,气体在通过无颗粒区域时流速增大越明显。

通过对比图6(b)和图6(c)可知,由于孔隙率越大,局部流速增大越不明显,导致流场域中CO2质量扩散速率随颗粒孔隙率增大而逐渐减小,以及在未达到吸附平衡的同一时间下ZIF-8吸附剂内所吸附的CO2量越少。

图7给出了出口处不同吸附剂孔隙率下的流场速度、颗粒内CO2浓度随时间的变化。由图7可知,孔隙率越大,流场速度越先达到稳定状态。孔隙率为0.50时,吸附床中流场区域的局部速度为0.000 63 m/s,CO2浓度为4.09 mol/m3;孔隙率为0.80 mm时,吸附床中流场区域的局部速度达到0.000 53 m/s,CO2浓度为3.24 mol/m3,这证实了前文中所说孔隙率越大,局部流速增大越不明显,流场域中CO2质量扩散速率越小,ZIF-8颗粒吸附CO2越少的观点。

图7 出口处不同吸附剂颗粒孔隙率下的流场速度、颗粒内CO2浓度随时间的变化

图8给出了不同孔隙率下ZIF-8吸附剂对CO2的吸附量随时间的变化情况。在其他条件相同时,不同孔隙率下的颗粒间传质阻力相等、颗粒内传质阻力不等。颗粒内传质阻力主要取决于CO2在ZIF-8吸附剂内的扩散系数,其中CO2气体在ZIF-8吸附剂中的扩散系数远小于在流场域中的扩散系数。因此,在吸附过程中,不同孔隙率下总传质阻力基本相等,从而达到吸附平衡所需时间基本相同。

图8 不同吸附剂颗粒孔隙率下吸附量的变化

4.3 排列方式的影响

图9给出了时间步长为300 000时不同ZIF-8吸附剂颗粒排列方式下的气体流速分布、CO2浓度分布和颗粒内吸附量分布。从图9(a)速度云图可知,在采用顺列和错列方式时,管道中吸附剂颗粒分布均匀,出现的局部速度大小基本相等,且位置分布规律。采用随机分布时,速度分布不均匀,局部增大的速度值超过顺列和错列分布时的局部速度最大值。

(a) 速度

由图9(b)和图9(c)可知,采用顺列分布的CO2浓度扩散速度更快,管道中CO2吸附量最大。这是因为随机分布时,虽然部分流体区域出现了更大的局部速度,产生了气体扰动,但由图9(a)可知,采用随机分布时,管道中有较多颗粒密集区域,其流速较小。且管道中吸附剂的填充率较大,颗粒密集区域较颗粒稀疏区域大得多,导致密集区域流速减小产生的影响大于稀疏区流速增大产生的影响。因此,在其他条件一定时,颗粒间传质阻力大小为:顺列<错列<随机,从而导致总传质阻力大小为:顺列<错列<随机。

图10为出口处不同吸附剂颗粒排列方式下的流场速度、颗粒内CO2浓度随时间的变化。由图10可知,吸附剂颗粒顺列分布时,吸附床中流场区域的局部速度为0.000 235 m/s,CO2浓度为3.41 mol/m3;吸附剂颗粒随机分布时,吸附床中流场区域的局部速度达到0.000 293 m/s,CO2浓度为3.13 mol/m3,这证实了前文中所说的采用顺列分布时局部速度较小,但CO2浓度扩散速度更快,管道中CO2吸附量更大的观点。

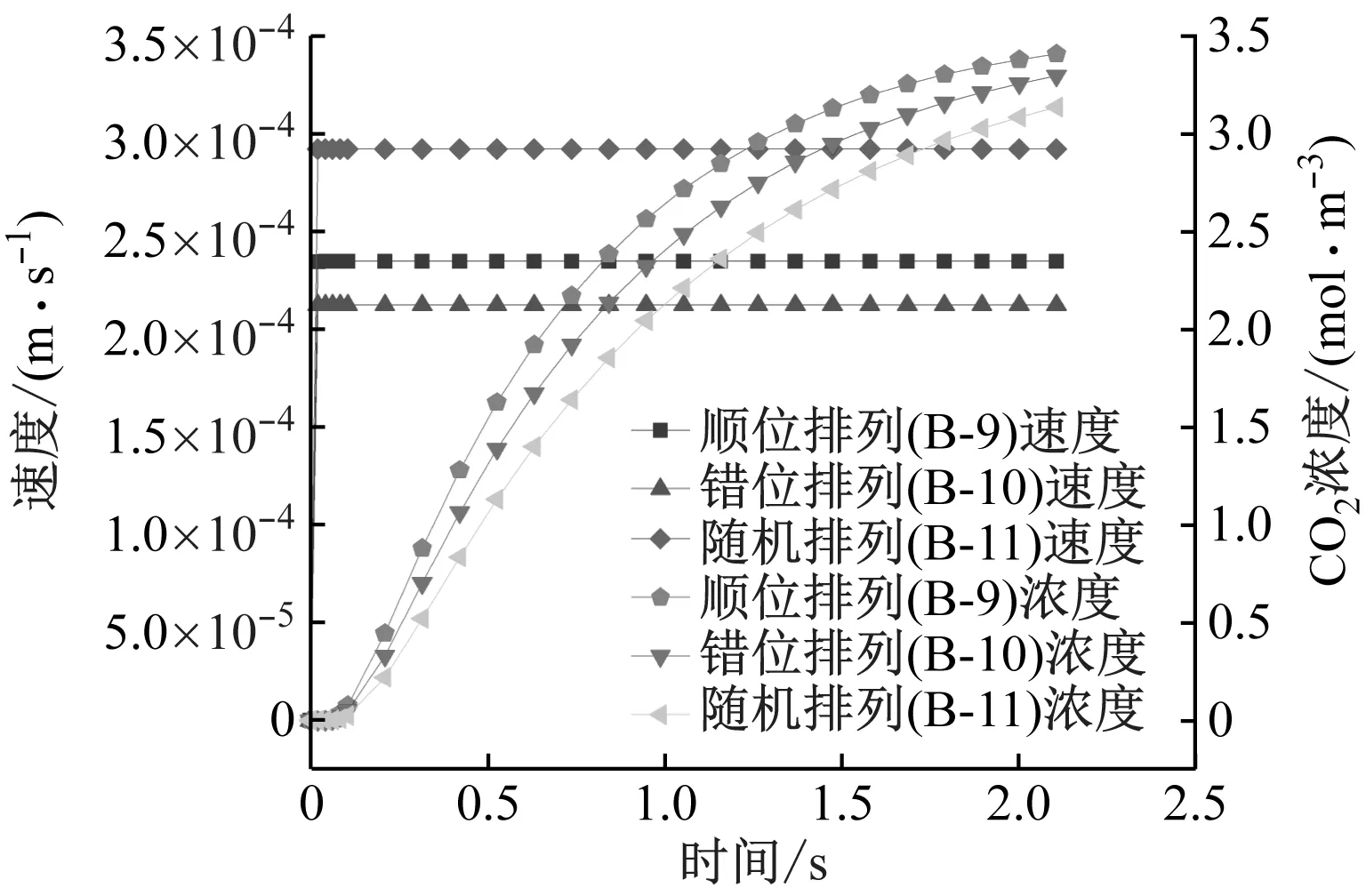
图10 出口处不同吸附剂颗粒排列方式下的流场速度、颗粒内CO2浓度随时间的变化

图11为不同颗粒排列方式下ZIF-8吸附剂对CO2的吸附量随时间的变化情况。由图11可知,由于3种颗粒分布方式的总传质阻力大小为:顺列<错列<随机,因此,顺列分布时达到吸附平衡所需时间最短,错列分布次之,随机分布最长。

4.4 敏感性分析

图12给出了不同影响因素下ZIF-8吸附剂对CO2的饱和吸附量。由图12可知,吸附剂粒径引起的吸附量变化幅度为0.007 mol/kg;吸附剂孔隙率引起的吸附量变化幅度为0.057 4 mol/kg;吸附剂颗粒排列方式引起的吸附量变化幅度为0.006 9 mol/kg。

图12 不同影响因素下ZIF-8吸附剂对CO2的饱和吸附量

为了找到对ZIF-8吸附CO2的饱和吸附量影响最大的参数,利用极差分析法分析模拟结果。对图12进行分析后得到表2所示的极差分析结果。其中K1、K2、K3、K4为在同一因素下的相同水平试验结果的总和;k1、k2、k3、k4则为K1、K2、K3、K4的平均值;Rj表示不同因素的极差。由表2可知,吸附剂孔隙率的极差Rj为0.054 4,说明它对饱和吸附量的影响最大,颗粒排列方式的极差次之,粒径的极差最小,为0.007 2。因此,ZIF-8吸附剂孔隙率对CO2吸附过程的影响更加敏感。在ZIF-8吸附剂的制备与实际工程应用中,应当优先调控吸附剂的孔隙率,以此调控对CO2的吸附量。

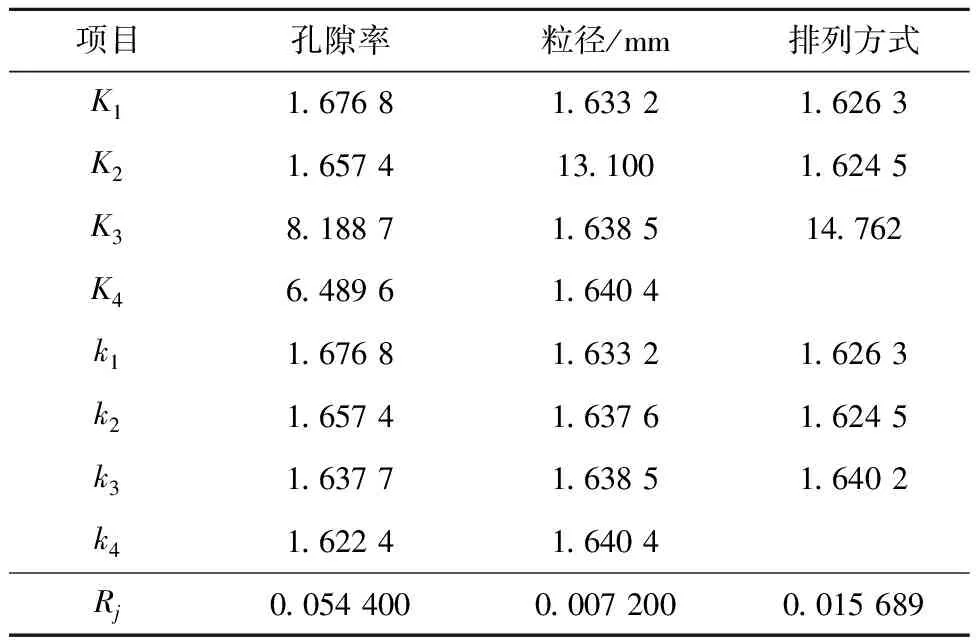
表2 极差计算分析结果

5 结 论

(1) ZIF-8吸附剂孔隙率对吸附过程中速度及浓度分布影响较大。在其他条件一定时,孔隙率越小,达到吸附平衡时吸附量越大,但同时局部流速增大越明显。因此,对孔隙率在0.50～0.80的ZIF-8材料进行工程应用时,宜采用孔隙率较大的ZIF-8吸附剂吸附CO2,避免因流速过大造成局部吸附不充分的风险。

(2) 在其他条件一定时,粒径越大,颗粒分布越不均匀,局部对流作用越强。因此,对粒径在0.05～0.20 mm的ZIF-8材料进行工程应用时,宜采用较大粒径的ZIF-8材料吸附CO2,有效缩短达到吸附平衡的时间。

(3) 在颗粒粒径和孔隙率一定时,与错列分布和随机分布相比,吸附床中ZIF-8颗粒采用顺列分布可以有效缩短达到吸附平衡所需要的时间。因此,在实际吸附过程中可采用颗粒顺列分布,尽量保证吸附床中颗粒分布的均匀性。

(4) ZIF-8吸附剂多孔形态及排列方式对CO2吸附量影响的敏感性依次为:孔隙率>排列方式>粒径。因此,在使用ZIF-8材料吸附CO2的实际应用中,应优先考虑对ZIF-8吸附剂孔隙率的选择,以达到吸附更多CO2的目的。