高位远程古滑坡既有变形特征和后续变形发展规律研究

李晓斌 白海军

1 陕西铁路工程职业技术学院工程管理与物流学院,陕西省渭南市站北街东段1号,714000 2 中铁四局集团第六工程有限公司,西安市大庆路3号,710000

近年来,我国滑坡灾害频发,其中,高位远程滑坡具有孕灾隐蔽、威胁范围大等特点,其危害性尤为严重,因此,以其为研究对象具有重要意义[1]。目前,已有不少学者对高位远程滑坡开展相关研究,如朱赛楠等[2]对该类滑坡的失稳机理及其防灾策略进行分析,殷跃平等[3]构建了该类滑坡发生的动力模型,高扬等[4]对该类滑坡解体时的动力效应进行研究。上述研究虽取得了相应成果,且各有侧重点,但总体来说针对该类滑坡的研究较少,且未涉及变形规律方面。因此,研究该类滑坡的变形规律具有重要意义。

在一般滑坡变形规律研究方面,总体来说,现有研究[5-7]多是基于现状监测条件下的统计分析,缺乏后续发展特征研究,且多侧重于累积变形量的统计,缺少滑坡变形序列的深入挖掘研究,尤其缺乏深入构建变形速率及加速度序列的相关研究,使得高位远程滑坡的变形规律分析仍有较大空间。

基于上述分析,本文将开展高位远程滑坡变形规律的综合研究。首先基于变形监测成果,应用统计分析方法开展既有变形特征分析,从累积变形、变形速率及变形加速度3个方面开展相应的变化规律分析及特征参数统计,以掌握滑坡变形的基础特征。为保证分析结果的全面性,并实现变形序列特征的深度挖掘,本文将分析序列确定为3类——累积变形序列、变形速率序列及变形加速度序列,即从累积变形量到变形加速度进行深度分析;同时,考虑到极限学习机[8]、Mann-Kendall检验(简称M-K检验)[9]及Spearman秩次检验[10]在岩土变形趋势判断中具有良好的适用性,因此,提出以此三者作为高位远程滑坡后续变形发展特征分析模型构建的基础。通过预测模型、M-K检验及Spearman秩次检验等方法分别开展3类变形序列的趋势变化特征分析,并结合既有变形特征分析结果,充分掌握高位远程岩质滑坡的变形规律。

1 古滑坡后续变形特征分析模型构建

滑坡变形具有较强的复杂性和不确定性,非线性特征显著,该特征在高位远程岩质滑坡变形中表现尤为突出,因此,滑坡监测数据并不一定完全代表滑坡真实变形,可将其表示为:

y(t)=z(t)+b(t)

(1)

式中,y(t)为滑坡变形监测数据;z(t)为滑坡变形真实信息,命名为真实变形分量;b(t)为滑坡变形的不确定信息,由监测误差、环境变化等造成,命名为不确定变形分量。

1.1 累积变形序列分析模型构建

在以往研究成果中,小波分解[11]、经验模态分解[12]已被广泛应用于式(1)中的分解处理,但其均侧重于分解序列的固有特性,存在一定不足,因此,Christiano Fitzgerald滤波[13](简称CF滤波)应运而生,其具有更强的带通特性,可分解滑坡变形数据。

在CF滤波[13]基础上,将分解效果评价指标设定为信噪比SNR和均方根误差RMSE:

(2)

(3)

式中,ps为变形信号的原始功率,pn为变形信号处理后的功率,n为分解序列的样本数,fi为变形数据的原始信号,f′i为变形数据处理后的信号。按照2个指标的构建原理,SNR值越大越好,RMSE值越小越好。

同时,为充分保证分解处理过程的准确性,进一步提出通过粒子群算法(particle swarm optimization,PSO)优化CF滤波过程中的模型参数,并将其优化过程表示为:

1)初始化设置PSO算法的基础参数,如将种群规模设置为400,最大迭代次数设置为650等。

2)以信噪比和均方根误差构建适应度函数,先计算出各粒子的初始适应度值,再确定初始全局最优适应度值。

3)不断更新、改变粒子状态,随即计算出新状态下粒子对应的适应度值,将其与全局适应度值对比,以实现迭代寻优。

4)当完成寻优后,输出寻优结果。

最终将滑坡变形数据的分解模型确定为PSO-CF滤波,即通过其将滑坡变形数据分解为真实变形分量和不确定变形分量。

考虑到滑坡变形数据已进行分解处理,因此后续预测模型也应相应构建。极限学习机(extreme learning machine, ELM)操作较为简便,非线性预测能力较强,本文以其构建真实变形分量的预测模型。

根据ELM模型的基本原理,其训练过程为:

(4)

式中,tj为真实变形分量的预测值,l为隐层节点个数,βi、wi为权值向量,g(x)为激励函数,xj为输入层信息,bi为阈值向量。

在ELM模型应用过程中,其对噪声较为敏感,会影响映射过程的准确性。为解决该问题,Huang等[14]引入正则化系数来降低噪声和映射的随机性,构建出KELM模型。但是,随着研究的深入,发现KELM模型的单核结构无法排除核函数的敏感性,因此,进一步将局部核和全局核融合,构建出MKELM模型,以进一步增加预测模型的泛化能力。

MKELM模型可在较大程度上保证核函数的最优性,但其权值向量和阈值向量均是随机产生,客观性仍待进一步优化。为解决该问题,进一步提出通过海鸥算法(seagull optimization algorithm, SOA)进行优化处理。因此,将滑坡真实变形分量的预测模型确定为SOA-MKELM模型,且考虑到真实变形分量的预测结果也会存在一定的预测误差,将其误差叠加至不确定变形分量中,以得到新的不确定变形分量。

广义回归神经网络(generalized regression neural network,GRNN)具有显著的非线性预测能力,对不确定信息的预测能力强,因此以其构建不确定变形分量的预测模型。该方法的原理参考文献[15],本文不再赘述。

综上所述,将累积变形序列的分析模型确定为SOA-MKELM-GRNN模型。

在滑坡变形预测模型构建基础上,如何通过其预测结果合理判断滑坡变形程度仍有待解决。为合理构建滑坡变形等级划分标准,引入现状速率V和预测速率Vc,前者主要由现有监测成果统计得到,后者主要通过外推预测结果统计得到,且由于外推预测周期数设定为4,因此两者的求解期数均确定为4,即现状速率V是由实测的最后4个周期统计得到,而预测速率Vc是由外推预测的4个周期统计得到。

结合以往经验,再进一步将累积变形序列条件下的变形程度等级划分标准设计如表1所示。

表1 累积变形序列条件下的变形程度等级划分Tab.1 Classification of deformation degree under cumulative deformation sequence

1.2 变形速率序列分析模型构建

由于变形速率值较小,通过变形预测难以保证其预测精度,提出利用M-K检验开展速率序列的发展趋势评价[9]:

(5)

式中,S为初步统计量;var(S)为初步统计量的特征参数,计算表达式为[n(n+1)(2n+5)]/18,其中,n为分析样本数。

通过Z值即可开展变形速率序列的发展趋势评价,具体评价标准为:当Z>0时,滑坡变形速率具有上升趋势;当Z<0时,滑坡变形速率具有下降趋势。Z绝对值越大,其对应的趋势程度相对也越大。结合M-K检验的基本原理,在相应显著水平a条件下,可查得对应的Za值,因此可通过a水平设定来对速率变形序列的趋势程度进行分类(表2)。

表2 变形速率序列的趋势程度分类标准Tab.2 Classification criteria of trend degree of deformation rate sequence

1.3 变形加速度序列分析模型构建

类比变形速率分析模型的构建过程,为合理评价变形加速度序列的发展趋势,引入Spearman秩次检验,以其构建变形加速度序列的分析模型。结合Spearman秩次检验的基本原理,将变形加速度序列设定为{Xi;i=1,2,…,n},再按照数值大小进行重新排序,得到{Yi;i=1,2,…,n},两个序列可按下式计算得到秩系数rs:

(6)

式中,n为样本总数。

通过rs值大小即可开展变形加速度序列的发展趋势评价:当rs<0时,变形加速度序列具有下降趋势;当rs>0时,变形加速度序列具有上升趋势。rs绝对值越大,其趋势性越显著,且在相应显著水平a条件下,可查得对应的Wp值,并以其确定相应的趋势等级。结合工程经验,将变形加速度序列的趋势等级划分标准设定如表3。

表3 变形加速率序列的趋势程度分类标准Tab.3 Classification criteria of trend degree of deformation acceleration sequence

2 工程实例与分析

2.1 工程概况

结合现场勘查成果,滑坡研究区属中高山地地貌,区内高程范围为3 100～3 700 m,平均坡度约40°,最大可达55°～70°,地形起伏相对较大。研究区内岩性以变质岩为主,多为板岩、变质石英砂岩,其次还分布有白云岩、灰岩等,岩层产状为184°∠53°,考虑到边坡倾向为195°,因此,该滑坡坡体具顺向坡结构。在水文地质条件方面,区内地下水类型主要为孔隙水和裂隙水。

为充分掌握滑坡形成特征,对滑坡样品进行14C测试,测得滑坡堆积物形成年代为2 700 a BP,说明该滑坡具有古滑坡特征。

滑坡整体平面形态呈条带状(平面形态见图1),主滑方向为195°,纵向长度3 000 m,前后缘高程范围为2 600～3 800 m,高差1 200 m,宽度变化相对较小,前缘宽度相对较宽,宽度范围为350～600 m,平均厚度约20 m,体积约1 600×104m3,属特大型滑坡。

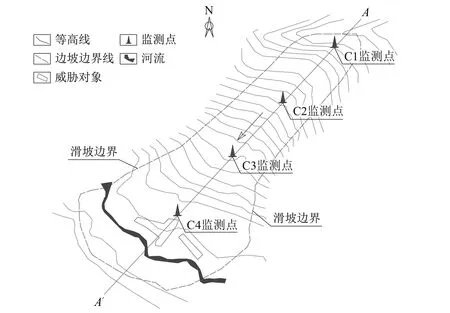
图1 滑坡平面形态示意图Fig.1 Schematic diagram of plane shape of landslide

在滑坡体岩性及结构方面,主要特征为:该滑坡规模较大,滑坡区基岩主要为变质砂岩与板岩互层,片理化发育,易形成层间软弱带,因此,该滑坡主要滑面位于基岩层内,属岩质滑坡。同时,第四系地层以崩坡积物为主,结构较为松散,渗透性强,易于降雨入渗,且由于其厚度分布不均,斜坡坡度较陡,会使得滑坡浅部形成一定规模的次级滑面。

2.2 既有变形特征统计分析

基于滑坡变形监测成果,通过统计分析开展不同变形序列的特征研究。结合坡体地层分布特征,共计选取4个监测点进行分析,其分布位置如图1所示;监测频率设置为1次/d,共计监测45期。

统计得到4个监测点的累积变形曲线,结果如图2所示。由图可知,4个监测点的累积变形具有持续增加趋势,其中,C1监测点的累积变形量达205.51 mm,C2监测点的累积变形量达143.53 mm,C3监测点的累积变形量达176.03 mm,C4监测点的累积变形量达96.57 mm,可见滑坡形成区的变形更大。

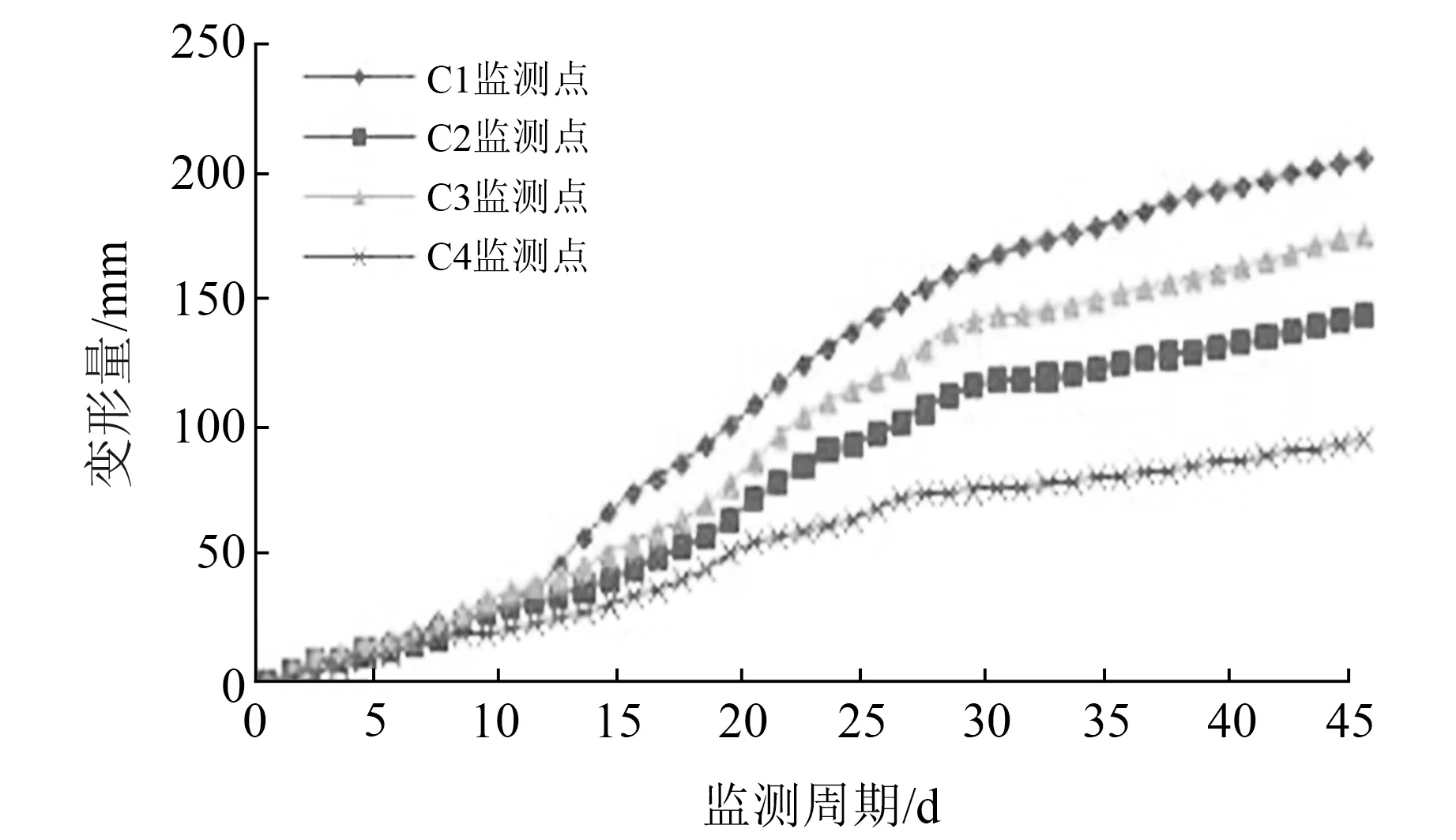
图2 滑坡累积变形曲线Fig.2 Cumulative deformation curve of landslide

2.3 后续变形发展特征规律研究

2.3.1 累积变形发展特征分析

按照研究思路,累积变形发展特征分析可通过变形预测实现,其分析过程包括PSO-CF滤波对变形数据的分解处理和SOA-MKELM-GRNN模型的逐步预测处理。

1) PSO-CF滤波对变形数据的分解处理结果。采用PSO算法对CF滤波进行优化处理,对其优化前后的分解结果进行统计,以验证PSO算法的优化效果。结果表明,CF滤波的信噪比值为36.91 dB,均方根误差为6.51×10-4mm;PSO-CF滤波的信噪比值为45.98 dB,均方根误差为4.73×10-4mm。由此可见,PSO-CF滤波具有相对更大的信噪比和更小的均方根误差,说明其分解效果相对更优,也验证了PSO算法的有效性。

为进一步验证PSO-CF滤波相较于其他分解方法的优越性,采用小波分解和经验模态分解进行类似预测,且为便于直观对比,将信噪比与均方根误差参数进行归一化相加,构建出评价指标M,其值越大说明分解效果越优,评价结果如图3所示。4类分解模型的评价指标M值存在较大差异,说明其分解效果不同,其中,PSO-CF滤波的M值为1.987,sym小波的M值为1.622,EMD模型的M值为1.728,db小波的M值为1.549。由此可见,PSO-CF滤波相较于其他3种分解模型具有明显的优势,充分表明该方法在本文实例中具有适用性。

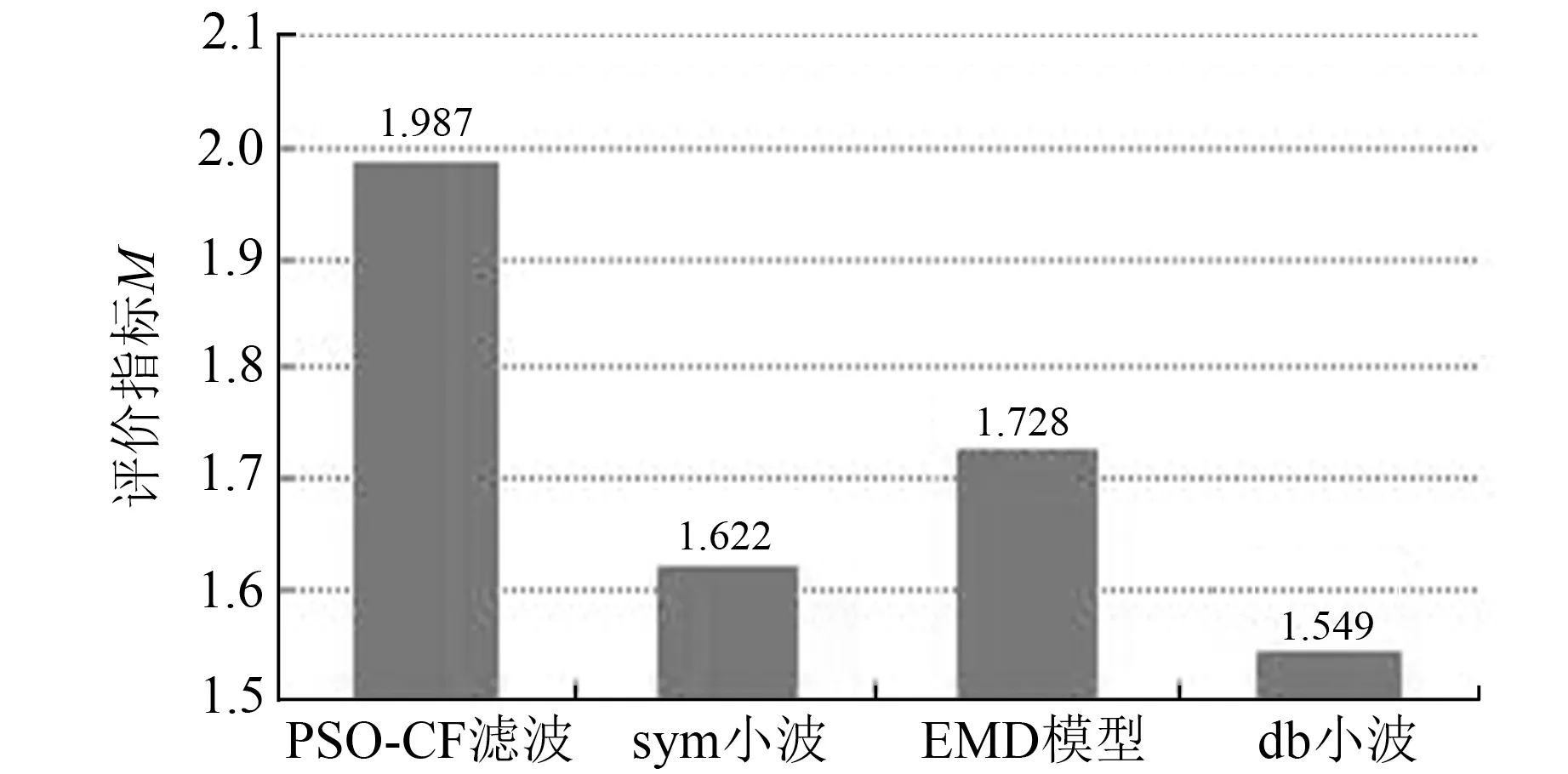
图3 不同模型的分解结果统计Fig.3 Decomposition results statistics of different models

综上可知,PSO-CF滤波在滑坡变形数据的分解处理中具有较好的效果,因此,利用其将变形数据分解为真实变形分量和不确定变形分量。

2)SOA-MKELM-GRNN模型逐步预测处理结果。在变形数据分解处理基础上,进一步开展逐步预测处理,且在该过程中,考虑到SOA-MKELM-GRNN模型是由基础模型逐步优化而来,因此,以C1监测点为例,对比分析不同模型的预测效果。

首先,对C1监测点真实变形分量在不同预测模型中的预测结果进行统计(表4)。由表可知,真实变形分量在不同模型中的预测效果存在差异,结合预测结果,对其特征参数进行统计:ELM模型的E值范围为3.55%～4.05%,平均值为3.78%,训练时间为302.18 ms;KELM模型的E值范围为3.11%～3.45%,平均值为3.28%,训练时间为274.31 ms;MKELM模型的E值范围为2.50%～2.77%,平均值为2.61%,训练时间为244.31 ms;SOA-MKELM模型的E值范围为2.18%～2.31%,平均值为2.24%,训练时间为214.72 ms。

表4 C1监测点真实变形分量的预测结果统计Tab.4 Statistics of prediction results of real deformation components at monitoring point C1

对比4类模型的预测结果可知,随着模型逐步递进优化处理,预测精度不断提高,训练时间也逐步减小,说明模型的收敛速度不断提高,验证了逐步优化过程的合理性。

其次,在真实变形分量预测基础上,再利用GRNN模型进一步开展不确定变形分量预测,得到C1监测点的最终预测结果(表5)。由表可知,

表5 C1监测点的最终预测结果统计Tab.5 Statistics of final prediction results of C1 monitoring point

C1监测点最终预测结果的E值范围为2.03%～2.22%,平均值为2.13%,训练时间为183.57 ms,相较于真实变形分量的最终预测结果,其在精度和收敛速度方面均有所提高,初步验证了SOA-MKELM-GRNN模型的有效性。

在C1监测点预测基础上,再对所有监测点进行类似预测及后续变形预测,且将后续预测周期数设定为4期,得到所有监测点的累积变形预测结果(表6)。由表可知,4个监测点的累积变形预测结果存在一定差异:C1监测点的E值范围为2.03%～2.22%,平均值为2.13%,训练时间为183.57 ms;C2监测点的E值范围为1.95%～2.16%,平均值为2.09%,训练时间为159.32 ms;C3监测点的E值范围为1.99%～2.20%,平均值为2.10%,训练时间为203.77 ms;C4监测点的E值范围为2.01%～2.18%,平均值为2.06%,训练时间为194.71 ms。

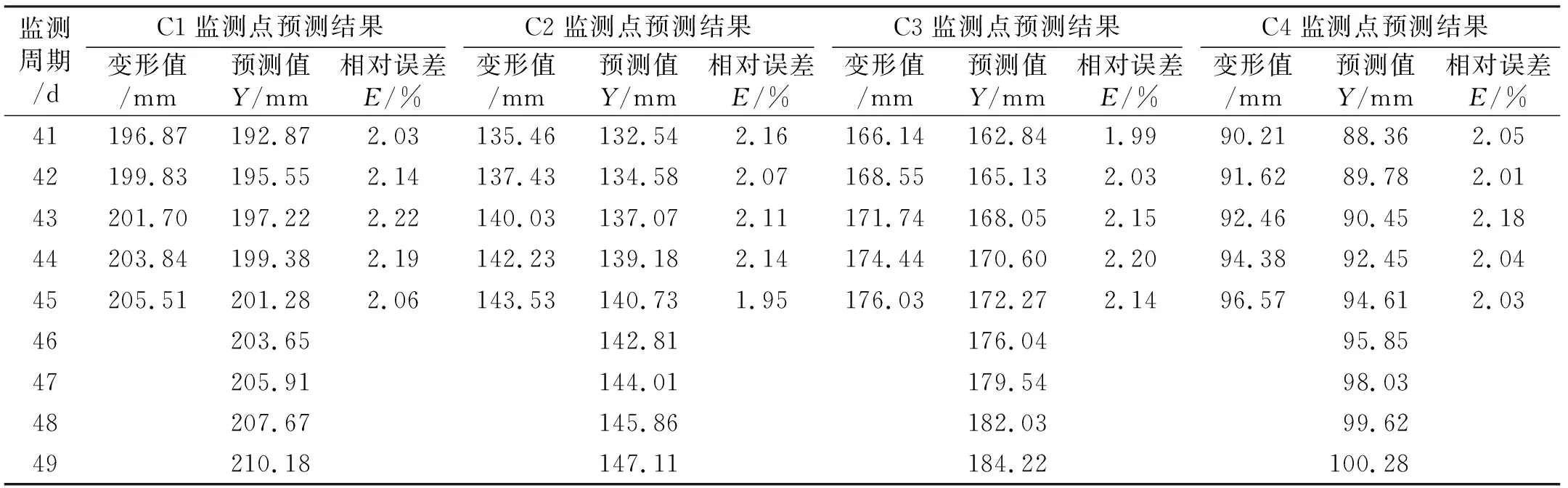
表6 滑坡累积变形的预测结果统计Tab.6 Statistics of prediction results of cumulative deformation of landslide

总体来说,四者预测效果相当,充分验证了SOA-MKELM-GRNN模型的有效性,且4个监测点的后续变形具有持续增加趋势。

结合表6结果,对累积变形序列条件下的变形程度分级结果进行统计(表7)。由表可知,4个监测点的累积变形程度存在一定差异,其中,C2监测点属1级,C4监测点属2级,其余2个监测点属3级。

表7 累积变形序列条件下的变形程度分级Tab.7 Classification of deformation degree under cumulative deformation sequence

2.3.2 变形速率发展特征分析

以各监测点变形速率序列为基础,通过M-K检验开展其发展特征分析(表8)。4个监测点变形速率序列的后续发展趋势存在较大差异,其中,C2和C4监测点的Z值小于0,具有下降趋势;其余2个监测点的Z值大于0,具有上升趋势。同时,按照趋势程度排序为:C3监测点(趋势程度非常强)>C2监测点(趋势程度较强)>C1监测点(趋势程度一般)>C4监测点(趋势程度一般)。

表8 变形速率序列的分析结果统计Tab.8 Analysis results statistics of deformation rate sequence

2.3.3 变形加速度发展特征分析

利用Spearman秩次检验开展变形加速度序列发展特征分析(表9)。4个监测点加速度序列的发展趋势存在较大差异,其中,C2和C4监测点的rs值小于0,具有下降趋势;其余2个监测点的rs值大于0,具有上升趋势,这与速率序列的分析结果一致。按照趋势等级划分,C1监测点的趋势等级为A级,C3监测点的趋势等级为B级,按趋势程度排序为:C4监测点>C3监测点>C1监测点>C2监测点。

表9 变形加速度序列的分析结果统计Tab.9 Analysis results statistics of deformation acceleration sequence

上述滑坡后续变形发展特征分析结果表明,不同序列的后续发展规律存在较大差异,但通过累积变形序列、变形速率序列及变形加速度序列的后续发展特征联合评价,能全面掌握其后续发展规律,具有较强的可推广性。

3 结 语

通过对高位远程顺层岩质古滑坡的既有变形特征及后续发展特征进行分析,得出以下结论:

1)滑坡既有变形特征显著,最大累积变形量已达205.51 mm,且变形速率序列和变形加速度序列的波动特征明显,其中,C1监测点的速率变化范围相对最广,速率均值也相对最大;加速度序列值则是前期相对较大,后期相对略小,说明该滑坡在监测前期变形加速更强。

2)在滑坡后续变形发展特征分析结果中,PSO-CF滤波能有效实现滑坡变形数据的分解处理,且SOA-MKELM-GRNN模型的预测效果较优,适用于滑坡变形预测。同时,M-K检验和Spearman秩次检验能有效实现变形速率序列和变形加速度序列的趋势判断,验证了两类方法的有效性。

3)不同分析序列的发展特征存在一定差异,其中累积变形序列会进一步增加,但不同监测点的变形速率及加速度变化趋势并不一致。