具有唯一平衡点的共存混沌系统及同步控制

张 萍

(沈阳化工大学信息工程学院 辽宁 沈阳 110142)

自从Lorenz发现第一个混沌吸引子以来,到目前为止混沌学已经发展了几十年。学者们从最开始的对混沌系统的动力学行为研究[1-2],逐步开始尝试实现对混沌系统进行在一定限制条件下同步控制[3-5],再到将混沌系统应用于图像加密、保密通信和生物医疗[6-9]等方面。因此,混沌学的研究开始从单一的研究混沌系统的动力学特性向实际应用方面转换[10-11]。一个结构简单并且动力学行为多样的混沌系统,在进行跨学科研究时往往能够起到决定性的作用。

混沌系统的种类层出不穷,但混沌吸引子的类型大抵可以分为单涡卷、多涡卷以及保守系统的类混沌吸引子[12-13],不同吸引子类型的出现主要受混沌系统结构中的非线性项以及初始条件的影响。近几年,混沌系统中吸引子共存现象受到了众多学者的青睐,忆阻器的使用对混沌系统[14-15]的混沌特性的影响尤为明显。一个简单的忆阻器以及结构简单的混沌系统相互结合产生吸引子共存的现象更能引起人们的兴趣。

本文对加入忆阻器的混沌系统的吸引子共存现象进行了探究,文章第一部分介绍了改进得到的新混沌系统及相应的混沌特性。第二部分对加入忆阻器的四维混沌系统的吸引子共存现象进行了相应阐述,并使用复杂度进行了验证。第三部分对新构造的四维混沌系统进行了电路仿真设计。最后一部分设计了自适应控制器,在参数不确定的情况下,实现了主从系统的同步控制。

1 混沌系统动力学分析

为探究混沌系统的吸引子共存现象,本文在经典Lorenz系统的基础上改进得到新的混沌系统为

(1)

其中,x、y、z为系统(1)的状态变量,a、b、c为未知参数,系统(1)含有7项且包含一个常数项,系统由同一未知参数调节,结构比较简单但含有丰富的混沌特性。

选取初始值(0.1, 0.1, 0.1),参数a=10,b=10,c=10时,系统(1)的相图以及时序图如图1。

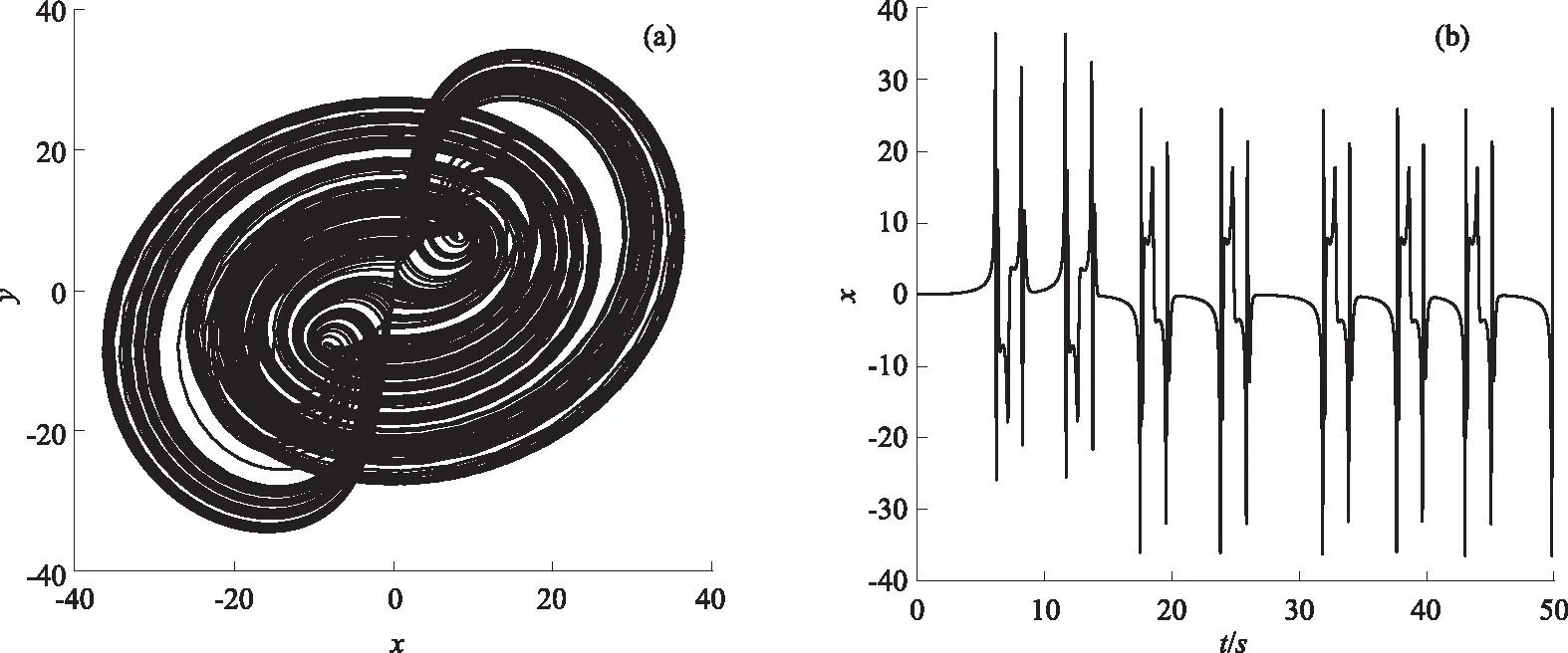
图1 相图和时序图

通过图1展现的系统(1)的混沌吸引子图像和时序图,能够清晰地看出系统(1)能够产生混沌吸引子,新提出的系统(1)具有混沌特性,为后续的动力学行为探究提供了先决条件。

2 负反馈构造四维混沌系统

具有忆阻器的混沌系统,由于忆阻器的特殊非线性特性,使系统容易产生多个共存吸引子。系统(1)虽然具有非线性有源忆阻,但由于系统的电路结构过于简单,不具备产生多个吸引子共存的能力。当系统电路存在多重均衡时,这种多重均衡会使系统在不同均衡周围产生不同的吸引子池。

本文考虑加入正弦函数作为反馈控制输入,得到新系统为

(2)

系统(2)在(x,y,z,w)→(-x, -y,z, -w)的坐标变换下保持不变,说明系统具有对称性。通常,混沌系统自身具有对称性的情况下,会使多个吸引子共存成为可能。

在对系统(2)的混沌特性进行探究时,使用李雅普诺夫指数图对系统(2)进行仿真,发现系统(2)在选取初始值为(0.1, 0.1, 0.1, 0.1),参数选取a=7.5,b=4,c=7,得到系统(2)的吸引子如图2所示。

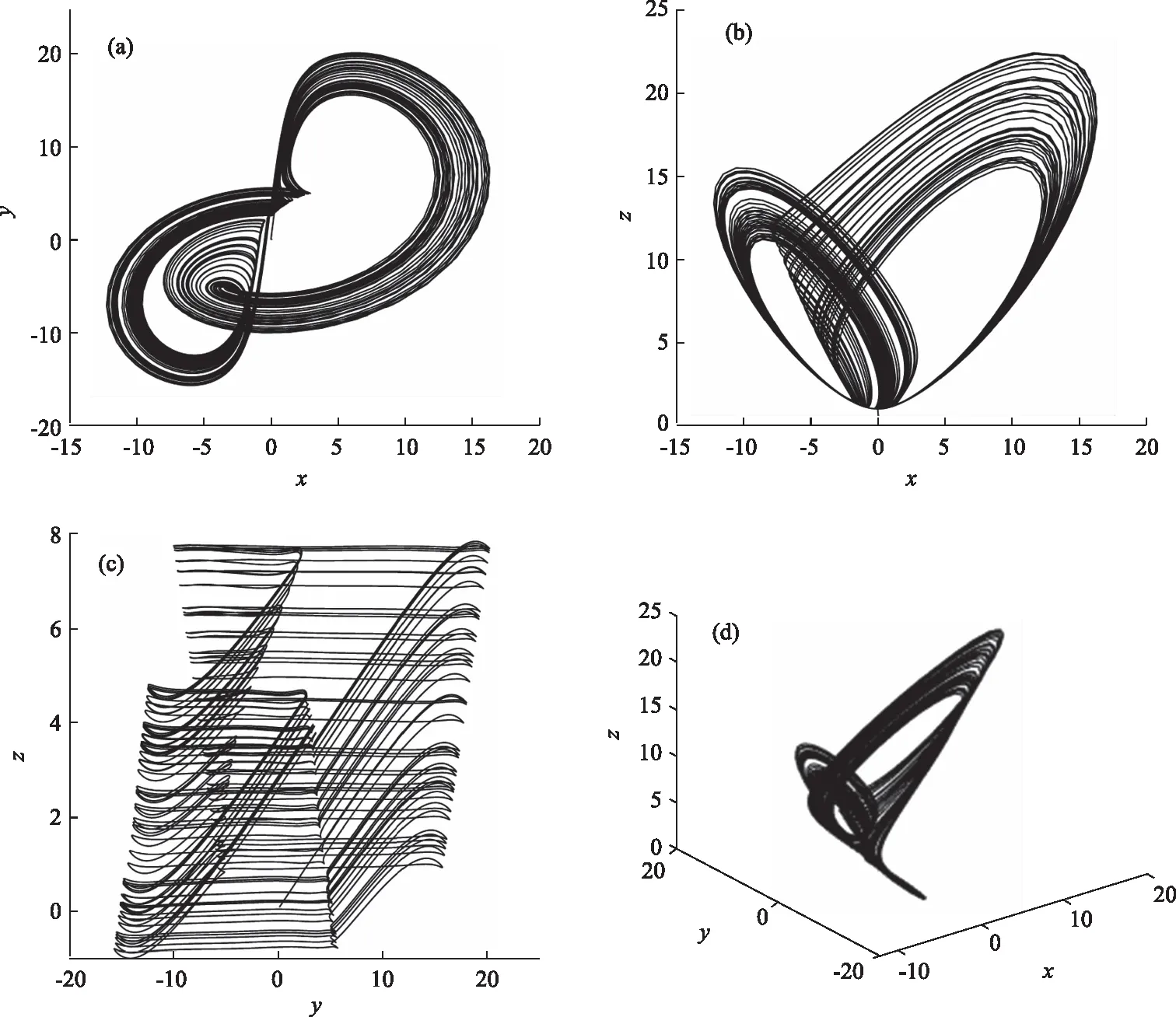
图2 相图和吸引子图

根据吸引子图和相图可以看出,系统运动轨迹复杂,具有重复、折叠以及延展的特性,但又是有界的。

3 混沌系统的吸引子共存现象

吸引子共存是混沌系统中重要且有趣的现象。为进一步探索系统(2)中吸引子的共存现象,现使用分岔图和相图对其进行进一步的探索。其中,a、b、c为未知参数。为探究新系统的吸引子存在情况,选取初始值为x01=(0.1, 0.1, 0.1, 0.1),x02=(-0.1, -0.1, -0.1, -0.1),参数设置b=4,c=5,a∈[1,8],得到系统(2)的分岔图如图3所示。为清晰地展现系统(2)在不同初始值时混沌吸引子的具体存在情况,选取多个具体的参数a的值,得到吸引子共存的相图(如图3所示)。

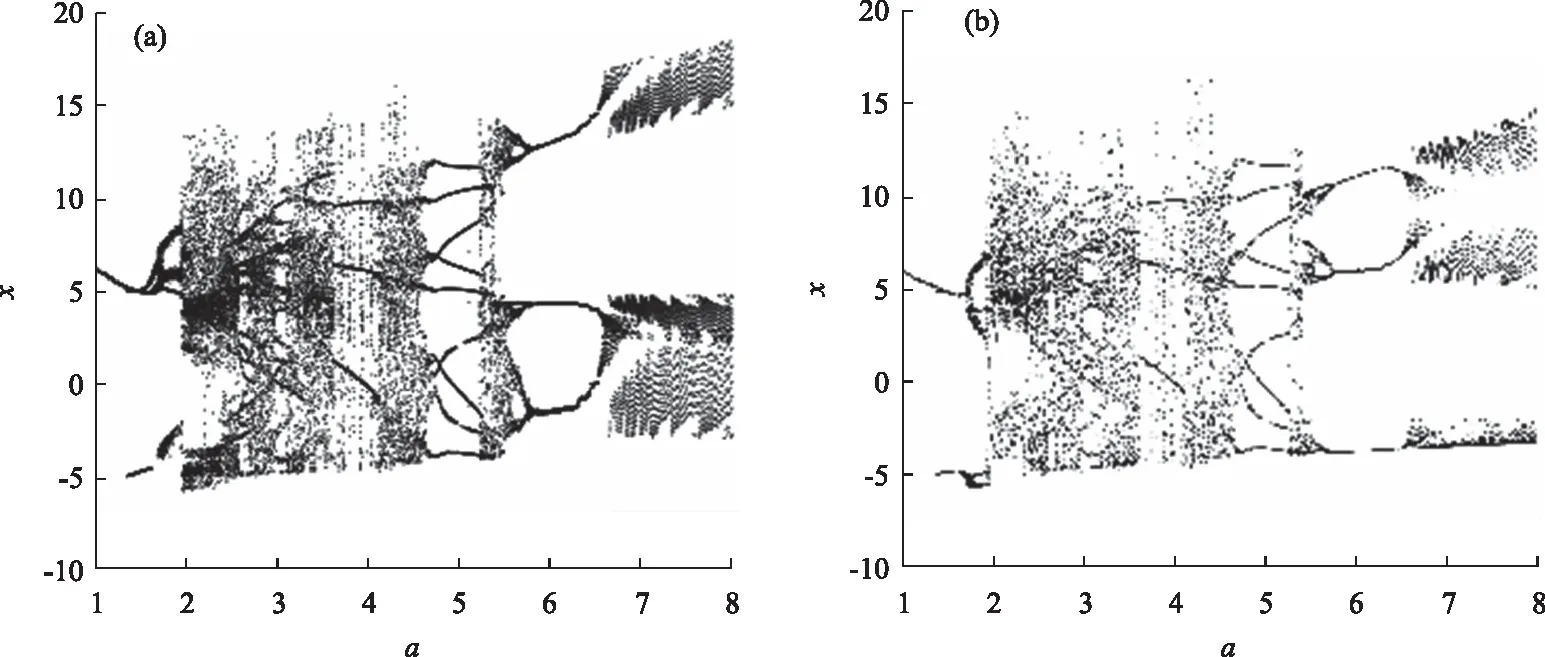
图3 不同初始值时系统(2)的分岔图

通过图3能够对比看出,系统(2)产生的分岔图中的密集点存在清晰的差异,说明系统(2)的动力学行为受初始值的影响。通过选取的不同参数得到的吸引子共存相图(如图4),能够看出系统(2)存在周期吸引子共存、倍周期吸引子共存和混沌吸引子共存,进一步展示了系统(2)的动力学行为。

图4 不同时期吸引子共存相图

4 新系统的复杂度分析

混沌系统的复杂度是描画混沌系统动力学特性的重要方法之一。本文主要使用SE算法和C0算法对比分析系统(2)的动力学行为。SE算法通过傅里叶变换域内能量分布与香农熵结合得到相应的谱熵值。C0算法主要将序列分解成规则和不规则部分,对于复杂度的计算主要为计算序列中非规则成分所占比例。系统(2)在初始值选取为(0.1,0.1,0.1,0.1)和(-0.1, -0.1, -0.1, -0.1),参数设置b=4,c=5,a∈[1,8]时的复杂度对比分析图如图5所示。

图5 复杂度分析

通过图5中的复杂度对比分析图能够清晰地看出,系统(2)在初始值的选取值不同时,复杂度存在明显的差异。图5中的复杂度变化规律与图3中的分岔图中的密集点的存在情况趋于一致,说明复杂度验证分析法有效性。

5 电路设计

为验证系统(1)和系统(2)电路实现的可行性,搭建的电路图如图6所示。

图6 系统的电路仿真图

图6中乘法器(AD633)的输出增益为1,运算放大器(LM324M)等相关组件,分别用于加法、减法和积分等相关运算。对图6应用基尔霍夫定律,得到微分方程

(3)

通过比较系统(2)与上式,选取参数b=4,c=7得到

(4)

通过改变电阻R1的阻值,能够得到系统(2)在参数a的不同取值时的吸引子。本文选取参数a的取值为a=3,4.5,7,10,电阻R1对应的电阻值分别为333.33 kΩ、222.22 kΩ、142.86 kΩ、100 kΩ,得到相应的电路仿真吸引子图如图7所示。

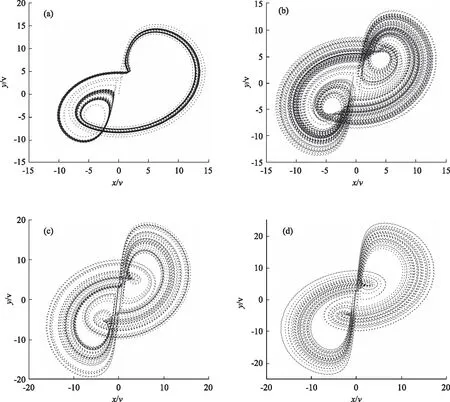
图7 各种时期x-y通道的吸引子图

通过各时期x-y通道的吸引子图,能够清晰地观察到电路仿真的结果与数值模拟的结果一致,进一步解释了系统(2)的复杂动力学特性。

6 自适应同步控制

6.1 理论分析

取式(2)转换为下列形式,作为驱动系统为

(5)

对应驱动系统为

(6)

将同步误差定义为

(7)

因此,可以得到同步误差系统为

(8)

考虑设计自适应控制器为

(9)

其中,k1、k2、k3、k4为正增益常数。

将式(9)代入(8)可得,闭环误差动态方程为

(10)

设置参数估计误差为

(11)

因此,方程(10)可以转换成

(12)

对方程(11)进行微分可得

(13)

取李雅普诺夫函数为

(14)

对其求导可得

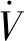
(15)

(16)

所以,可以得到

(17)

因此,由李雅普诺夫稳定性理论可知,误差系统是渐近稳定的,驱动系统与响应系统能够达到同步。

6.2 数值仿真

为了验证控制器的有效性,通过仿真实验对其进行验证。取驱动系统的初始值为(-1, 2, 0.1, 2),响应系统的初始值为(1, 2, -2, 0),因此,误差系统的初始值为(2, 0, -2.1, -1),设置控制参数kn=20,n=1,2,3。基于上述数据进行仿真,可以得到同步误差结果(如图8所示)。

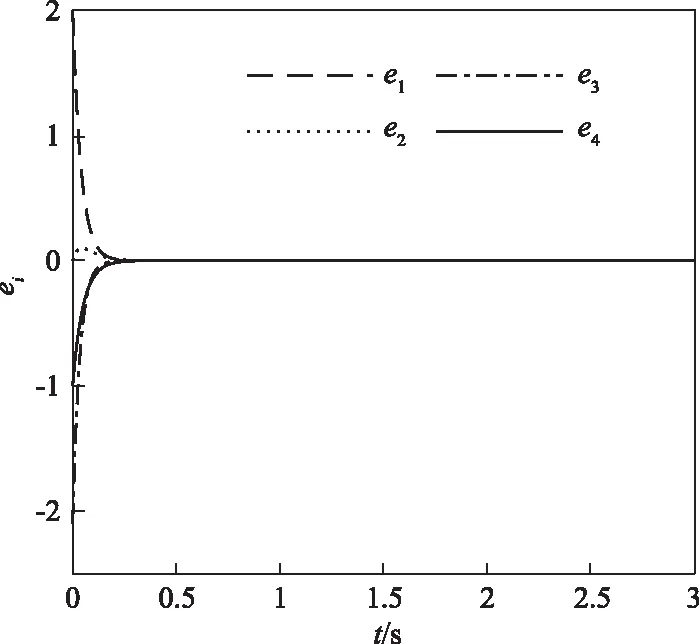
图8 同步误差仿真结果

根据图8同步误差仿真结果可以看出,系统很快达到同步,同步误差在0.5 s内,趋近为0。这验证了驱动系统和响应系统能在较短时间内达到同步。

7 总结

本文构建了一个结构简单的混沌系统,并通过负反馈引入忆阻器构造出新的四维混沌系统。文章对新系统的平衡点以及对称特点进行了阐述。通过分岔图和复杂度等方式,对新系统的吸引子共存现象进行了充分的说明。将新构造的四维混沌系统应用于电路仿真,为将系统应用于硬件实现等领域提供了理论基础。最后研究了对该混沌系统的同步控制,设计了自适应控制器,通过数值仿真验证是切实可靠的,符合实际应用。