带坞舱船舶尾舱消浪装置消浪性能研究

孙雷，杨雨田，韩易健，马玉祥

（大连理工大学 a.船舶工程学院 b.水利工程学院，辽宁 大连 116024）

尾部半开敞式坞舱的船舶不论是在军事领域，还是在工程建设领域，都能够发挥出重要的作用。在正常作业时，其尾部的半开敞坞舱处于半浸没状态，形成与外部连通的自由液面。在外部波浪的作用下，舱内的自由液面会形成波浪，形成有害的波浪砰击，影响舱内装备的正常作业。因此，有必要对坞舱内水体的波浪消减和控制方法开展深入研究，需要提出一套适用于带坞舱船舶尾舱内波浪特性的消浪装置方案。

目前对半开敞液舱数值模拟的研究成果还比较少，且大多都基于计算流体力学（CFD）方法。Bass等[1]采用Flow-3D 对4 级海况作用下具有半开口液舱的登陆平台进行了模拟，并分析了平台舱口的运动状况和舱内的波高情况。Cartwright 等[2]采用SPH 方法对具有半开口液舱的登陆平台进行了模拟。胡晓庆[3]对Wigley 船型进行了改造，增加了尾部船坞，之后用Fluent 对该船型进行了一系列的数值模拟，发现船体运动是否受到约束对船舱内的流场波浪波面起伏具有很大的影响，并指出对尾舱内进行合理的消浪装置设计具有重要意义。物理模型试验也是研究复杂水动力问题的必要手段[4]。目前关于半开敞式液舱的物理模型试验还比较少，对于液舱问题的研究多为液舱晃荡试验[5]及月池试验[6]。Hopman 等[7]以荷兰海军登陆舰为原型进行了4 级海况下舱内流体运动的物理模型试验，发现舱内波面运动幅度与波浪周期有关。翁欢英[8]对不封闭舱容内部消波装置的设计选型进行了试验研究。Zheng 等[9]采用了变态比尺的方法（水平与垂直方向的比尺不同），在试验水池的深度有限的情况下，对港湾共振问题进行了研究。在使用变态比尺进行模型试验时，需要对原模型与变态比尺后的模型进行相似条件的验证[10]。

国内外学者一直致力于消浪装置的研究，对消浪装置的研究通常从理论研究、物理模型试验和数值模拟等3 个方面展开。理论研究方面，Ursell 等[11]在有限水深情况下，对直立挡板进行了研究，给出了透射系数的计算公式。Heins[12]研究了水平板在有限水深水域的水面处的透射系数。Stoker 等[13]对单块水平板在长波作用下的消浪性能进行了研究。Siew 等[14]研究了下潜式水平板，用简单形式的方程描述了其在长波作用下的反射系数和透射系数。物理实验研究方面，Paterapanich 等[15]进行了物理模型试验，对水平板的板宽和水深等参数进行了研究。Murakami 等[16]对斜板式消浪装置进行了研究。Liu 等[17]研究了潜式双层水平板消浪结构。王国玉等[18]利用物理模型试验的方法研究了二维规则波作用下开孔斜板的消浪性能。数值模拟方面，Yu 等[19]基于势流理论研究了带孔水平板上的波浪运动，讨论了不同因素对其能量损耗的影响。Carter 等[20]研究了波浪经过平板结构时平板下方的逆流现象。Guan 等[21]研究了不同型式挡板的制荡消波作用。Cho[22]利用ALE 有限元方法对燃料储罐结构内挡板的抑制作用进行了研究。Zang 等[23]得出了多孔挡板的长度、孔隙率等因素对波浪的影响。丁俊杰等[24]利用CFD 方法对透水式多层开孔板进行了数值模拟研究，研究了消浪装置的反射系数和透射系数与入射波波长和波高的关系。任冰等[25]基于VOF 方法，模拟研究了海绵层结构在水池实验中的消浪系数。

综上所述，目前对于半开敞液舱的研究成果较少，主要方法为CFD 数值模拟和物理模型试验。消浪装置的研究已经非常丰富，有众多学者在这一领域进行开拓性的研究。其中，数值模拟由于其低廉的成本、可靠的求解结果，在工程领域得到了广泛的应用。本文针对荷兰皇家海军两栖运输船，使用多孔挡板为基础，给出了开孔板消浪装置的选用与布置方案，并使用CFD 方法模拟带有消浪装置方案的船舶响应，监测船舶的运动响应和舱内多个监测点的波高情况，评估给出的消浪装置方案的消浪性能。

1 理论及数值方法

1.1 基础理论

1.1.1 基本控制方程

本文数值模型的建立是基于不可压缩黏性流体的基本假定。流体运动遵循质量守恒定律、动量守恒定律和能量守恒定律。

1）连续性方程（质量守恒方程）。连续性方程指出流体在流经某一控制体时，流入控制面与流出控制面的流体质量之差，必然等于该控制体的流体质量增量，见式（1）。

式中：V为流体微元控制体；A为流体微元控制体的表面（也称控制面）；t为时间；ρ为流体密度；v→为控制面上的流体速度矢量；n→为流体控制面上一点的法向单位矢量。表达式在直角坐标系下的微分方程见式（2）。

式中：x、y和z为流体位置坐标值；u、v和w为流体在x、y和z方向上的速度分量。可将式（2）进一步写成张量形式：

对于不可压缩流体，密度ρ为常数，式（3）可简化为：

2）N-S 方程（动量方程）。动量方程表明单位体积控制体内流体动量的时间变化率等于作用其上的力，见式（5）。

式中：fx、fy和fz分别为体积力在x、y和z方向上的分量；p和τ为流体表面力的法向应力分量和切向应力分量。当引入平衡压强即静水压强，并引入Stokes 假定（法向应力和切向应力与线应变率和角变形率呈线性关系）时，动量方程（5）转化为N-S 方程，其表达式张量形式：

当忽略黏度时，表达式简化为式（7）。

其分量形式：

3）能量守恒方程。能量守恒代表控制体中能量的增加等于外力对其做的功，见式（9）。

或写成：

式中：T为温度；Cp为流体的比热容；k为传热系数；ST为黏性耗散项。

1.1.2 拓展型缓坡方程

当舱门开敞时，尾部坞舱为半封闭环境水域。对于尾部坞舱内的水体晃荡，波浪于船底底部的透射可以看作一种能量损耗，只影响水体晃荡的强度，而不改变舱室水体运动的固有频率。此外，舱室水体是在不透水的底边界和垂向舱壁边界的约束下运动的，与港湾振荡现象最为接近。因此，可采取广泛应用于港湾振荡研究的拓展型缓坡方程模型（EMSE）进行尾部坞舱内水体的固有频率和波浪运动形态的计算。缓坡方程控制方程见式（11）。

式中：∇为平面微分算子，∇=(∂/ ∂x,∂/∂y)；φ为速度势；k、C和cg分别为波数、波浪相速度和群速度，它们由以下式（12）和（13）决定。

式中：h为水深。控制方程和边界条件构成封闭的方程组后，才能对物理现象进行合理的描述。

在水体共振研究中，常用的边界为混合元边界，其表达式为：

1.2 数值模拟

本文采用荷兰皇家海军两栖运输船[7]，其主尺度参数见表1。本文对船舶进行等比例建模，船舶实体及船体几何模型如图1、图2 所示。其中，为了方便计算与后续分析，本文对该船舶的尾部舱室进行了简化。由于船舶原舱室在舱内靠近首端部分有一个上升的斜坡，因此将船舱分成了2 个不同高度的部分。本文将舱室简化为简单的长方体，其中舱长为52 m，舱宽为15 m，舱内水深为1.2 m。

图2 船舶模型Fig.2 Ship model

表1 船舶主尺度参数Tab.1 Main dimension parameters of ship

表2 半开敞状态下舱内水体固有周期Tab.2 Natural period of water body in cabin under semi-open state

用EMSE 模型计算尾部坞舱内水体的固有频率和波浪运动形态。舱室的响应曲线和固有模态的周期如图3 所示，4 个固有周期的瞬时波面如图4 所示。

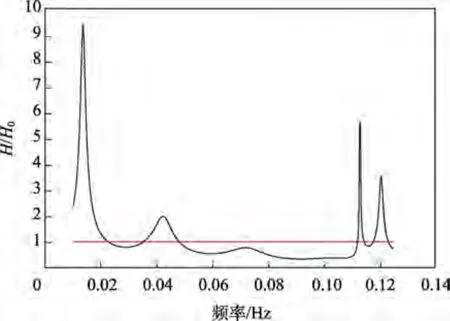
图3 半开敞舱室响应曲线Fig.3 Response curve of semi-open cabin

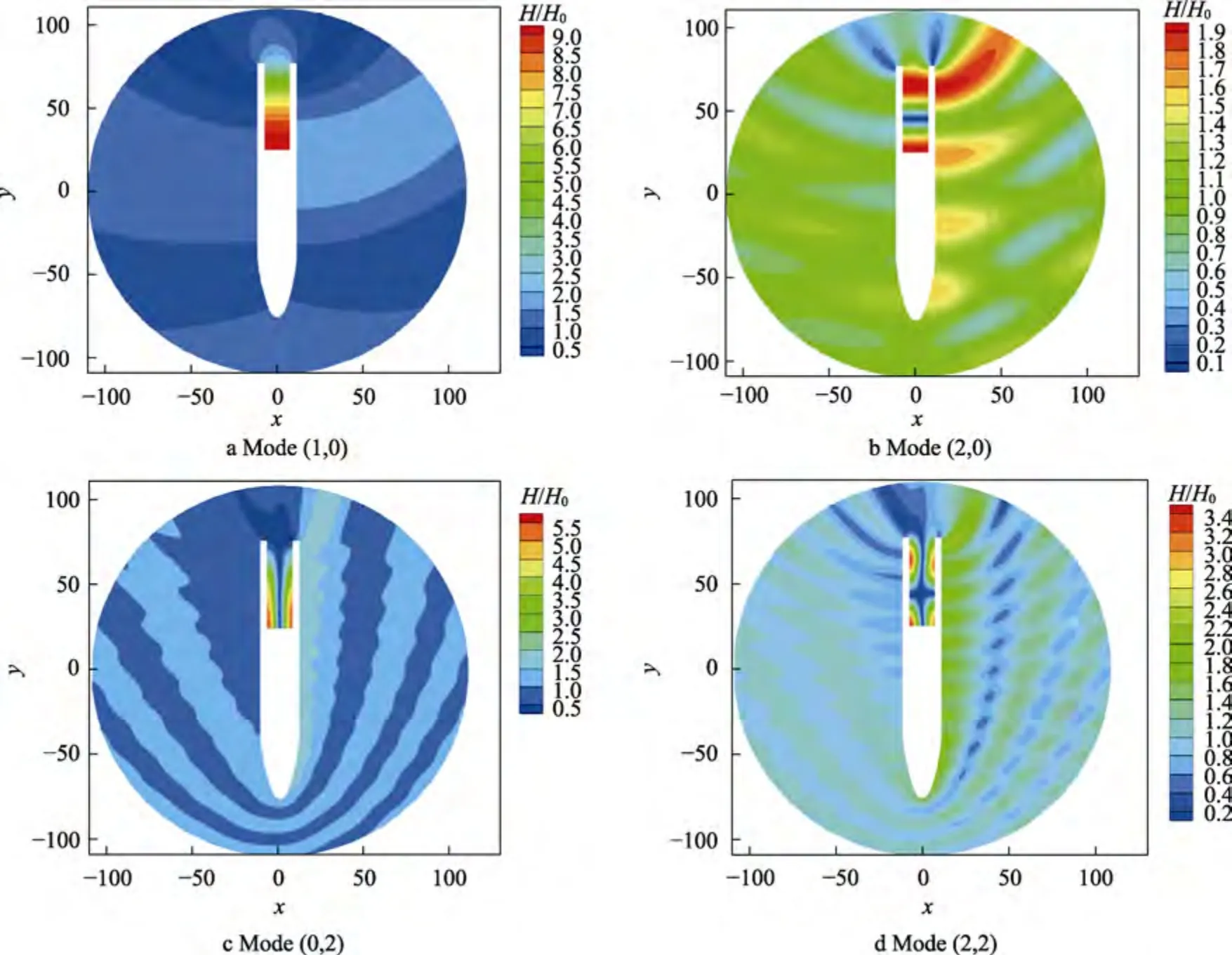
图4 固有模态瞬时波面Fig.4 Natural modal instantaneous wave surface

本文对该船舶模型进行计算，得到其纵摇、垂荡和液舱耦合共振周期为 11.393 4 s。该船舶的纵摇RAO 曲线如图5 所示。

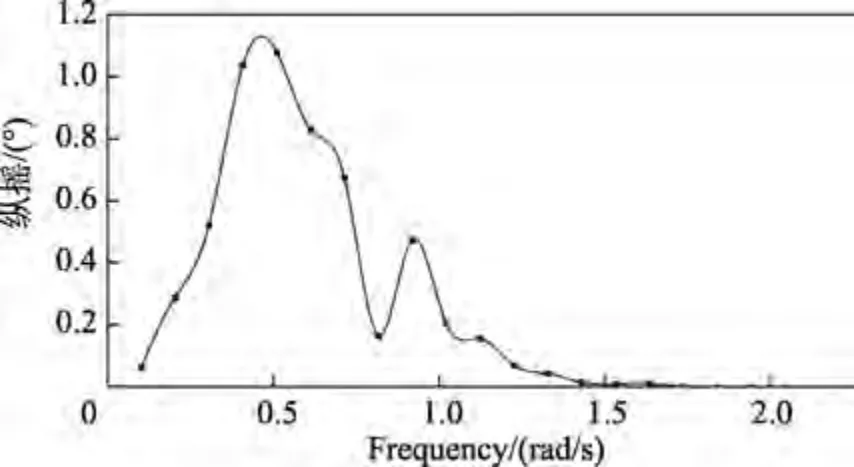
图5 纵摇RAO 曲线Fig.5 Pitch RAO curve

本文在基于CFD 数值模拟软件Star-CCM+中的网格划分及网格收敛性验证基础上，分别采用网格基础尺寸为15、25、35 m 等3 种不同的网格尺寸进行模拟（如图6、图7 所示），其中网格尺寸为25 m 的网格总量约为500 万。输出船舶的纵摇时程曲线（如图7 所示），可以看出，网格基础尺寸为25 m 时已经达到收敛，故采取基础尺寸为25 m 的网格划分方案。

图6 流域网格划分Fig.6 Watershed grid division

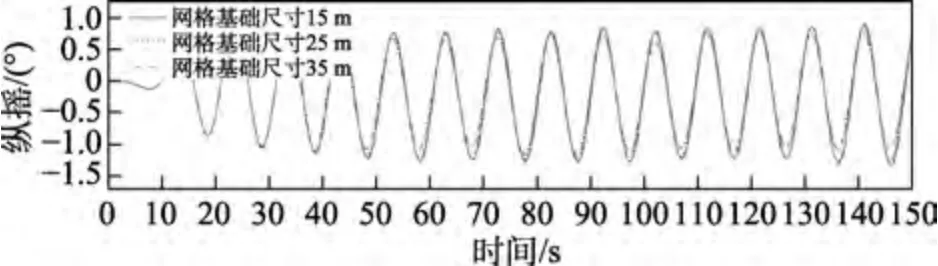
图7 3 种不同尺寸网格结果对比Fig.7 Comparison of grid results of three different sizes

经过分析，本文在荷兰皇家海军两栖运输船的坞舱内分别设置了如下4 种方案。

方案一：不设置消浪装置的空舱对照组，如图8a 所示；

图8 不同布置方案模型Fig.8 Models of different layout schemes:a) scheme 1;b) scheme 2;c) scheme 3;4) scheme 4

方案二：仅布置首端开孔板消浪装置，孔隙率为7.4%，如图8b 所示；

方案三：仅布置侧壁开孔板消浪装置，孔隙率为8%，如图8c 所示；

方案四：同时布置首端和侧壁开孔板消浪装置，孔隙率分别为7.4%和8%，如图8d 所示。

本文采用多孔介质区域模型对多孔板结构进行等效替代，对由多孔板结构组成的消浪装置进行CFD数值模拟。这种处理方法的优点在于无须考虑多孔板的细小空洞，节省大量计算资源。由于消浪装置设置在舱室四周，且本身由多孔介质模型组成，因此不会对坞舱内设备的正常出入及工作产生不利影响，而且坞舱内水体的固有频率也不会产生明显的变化。

在液体流过多孔介质区域时会经历一个降压过程。达西定律将流速与基于渗透率测量的压力梯度联系起来，见式（15）。

式中：μ表示流体的分子黏度；kp表示渗透率（被认为是多孔介质的一种内在性质）；vs是通过介质的表面速度。随着流速的增加，流体流速与压力梯度的关系将会变得非线性，于是有了Forchheimer 方程：

在STAR-CCM+中，对于多孔介质区域的描述便使用了Forchheimer 方程，在单项流中，流体的压降Δp被定义为：

式中：vn为物面的法向速度；a和b为阻力相关系数；ρ表示界面处的流体密度。

多孔介质在流动方向上的长度L，将压降转换为压力梯度：

式中：α为惯性阻力相关系数；β即黏性阻力相关系数。

为了验证数值实验方法的正确性，采用相同的惯性和黏性阻力系数，分别对多孔板和多孔介质区域进行模拟。选取与本文消浪装置具有相同板厚与孔排布的正方形多孔板（如图9 所示），其边长为11.7 cm，圆孔的孔径为0.8 cm，孔隙率约为29.7%，板厚为1 cm。在相同流域与流速情况下，多孔板与多孔介质区域得到的数据曲线对比如图10 所示。

图9 多孔板结构Fig.9 Porous plate model

图10 多孔斜板模型与多孔介质区域得到的数据曲线对比Fig.10 Comparison of data curves between porous inclined plate model and porous media region

为了定量地探究消浪装置的消浪效果，在舱内x方向设置了24 个测点，y方向设置了7 个测点，共168 个测点。其中，x方向间隔 2 m，y方向间隔 2 m，原点在坞舱尾端开口与中纵平面交点处。每个监测点测得波面时程曲线，同时记录舱内波面侧视图和三维视图，用于后续分析，监测点示意图如图11 所示。波况设置见表3。

图11 舱内监测点布置Fig.11 Layout of monitoring points in the cabin

表3 波况参数Tab.3 Parameters for different wave conditions

2 结果和讨论

以波况1 为例，首先模拟对比了4 种方案的船舶运动响应，如图12 所示。可以看出，消浪装置的装载对船舶的响应情况几乎没有影响。

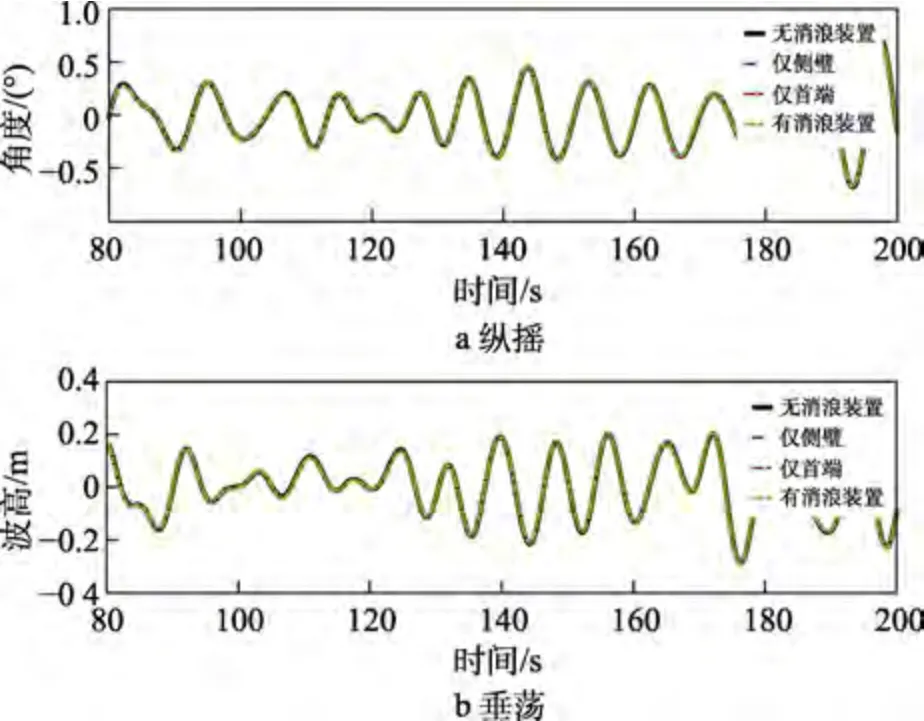
图12 运动响应时程曲线对比Fig.12 Comparison of motion response time history curves:a) pitch;b) heave

第一个较为明显的波浪在t=16.3 s 时到达船舱内部，如图13 所示。可以看出，波浪从坞舱尾端开口传至坞舱首端的过程中，在方案一、二中到达首端的波浪相较于方案三、四具有一个较为明显的起伏。这说明侧壁消浪装置对于入射波具有一定的削弱作用，但这种减小作用是十分有限的，并不能将任意波高的波都完全消除。

图13 t=16.3 s 舱内波面展示Fig.13 Wave surface in cabin when t=16.3 s:a) vertical view;b) partially enlarged view

从图14 可以看出，在随后的17.8 s，没有首端斜坡板的方案一、三出现了较为明显的反射波，而方案二、四则没有反射波的出现。可以看出，仅具有一个斜板的消浪装置便可以较好地消除反射波。之后，舱内便不断有入射波和反射波生成，并且这些入射波和反射波相互作用会形成新的波，这导致舱内的波面变得十分复杂。方案二中，首端消浪结构可以减弱反射波，但并不能完全消除。方案三中，坞舱尾端开口形成的入射波在侧壁装置的作用下会逐渐减弱，但后面形成的波高较高的波并无法完全消除，依然会发生如反射波相汇的情况。方案四则很少看到有入射波与反射波相汇的情况，且波浪不断衰减，如图15 所示。

图14 t=17.8 s 舱内波面展示Fig.14 Wave surface in cabin when t=17.8 s:a) vertical view;b) partially enlarged view

图15 t=89.8 s 舱内波面展示Fig.15 Wave surface in cabin when t=89.8 s

波况1 在4 种方案下舱内监测点的波高时程曲线对比如图16 所示。本文选取了几个具有代表性的监测点进行展示，监测点具体位置在每个曲线图的标题处标出，取波浪发展的80～200 s 时间段进行展示。从这些监测点中可以看出，相较于无消浪装置的波面，3 个有消浪装置的波面最大波高峰值明显得到了削弱，并且同时具有首端和侧壁消浪装置的消浪效果要优于仅有首端消浪装置和仅有侧壁消浪装置的情况。另外，不仅监测点的最大波高得到了削减，有消浪装置相较无消浪装置波面整体也明显更加平缓，这使得舱内结构物受到的砰击载荷更小，作业也更加安全。还可以看出，随着监测点的x值向坞舱尾端开口处移动，消浪装置的消浪效果也会渐渐减少，大约到x=30 m 处，消浪效果已经不太理想，说明本文给出的消浪装置方案主要作用于尾舱内部区域。这是因为该消浪装置的消浪机理为削弱入射波，并避免波浪与内壁的砰击，而在坞舱尾端开口处，波浪由于船舶的响应和外域波浪的共同作用，入射波刚开始产生，此时波浪并未与消浪装置发生作用，因此消浪装置在坞舱尾端开口区域作用并不大。

图16 舱内波面时程曲线对比Fig.16 Comparison of wave surface time history curves in cabin

此外，本文还定量地对消浪装置的消浪性能进行了分析。本文计算了每一个监测点的波浪曲线的能量，每种工况对所有监测点的能量求和，作为评定该工况下舱内波面能量的指标。之后，分别使用方案二、三、四的波面能量减去无消浪装置的方案一的能量，并求出该差值对于方案一能量的比例，以此来定量地评定削减掉的能量，见表3。可以看出，首端与侧壁消浪装置对该波况下的波面具有不错的消能作用，其中同时安装了首端与侧壁消浪装置的方案消掉接近40%的波面能量，这将为舱内的设备物资安全工作提供重要保障。

从表4 可以看出，本文给出的具有首端和侧壁消浪装置的方案四相较于没有消浪装置的空舱情况在多种不同的波况中，全部都可以消掉40%左右的波面能量。这将使船舶尾舱内的波面更加平稳，作业更加安全。事实上，由于坞舱尾端开口处的波浪几乎没有受到消浪装置的作用，消浪效果均发生在舱内的部分，因此如果只将舱中线内部的监测点的波面能量作为参考指标，消浪效果将会更好。基于此，本文选取舱内横坐标x=26 m 到x=48 m 的部分进行能量求和，得到结果见表5。

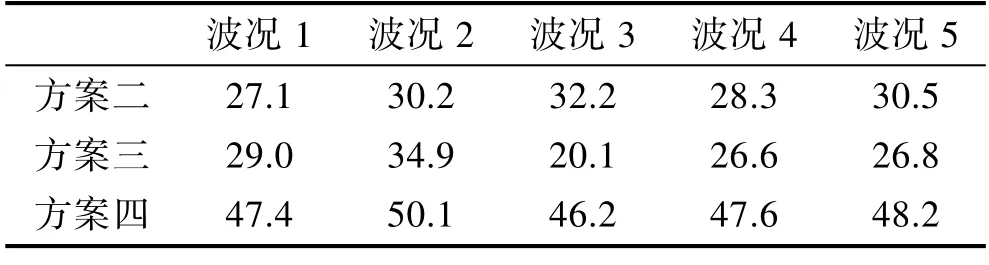
表5 舱中线以内不同波况下3 种方案相较于空舱削减掉的波浪能量Tab.5 Wave energy reduced by the three schemes under different wave conditions within ship centerline compared with that of the empty cabin%

从表5 可以看出，尾舱中线以内的部分消浪效果相较于整舱所有监测点的平均能量消浪性能得到了进一步的提升，能量削弱达到将近50%。这进一步说明了本文所给出的消浪装置的主要作用发生在舱内部分，并且进一步证实了本文消浪装置的有效性。

3 结论

1）不论是同时装有首端和侧壁消浪装置，还是仅装有一种消浪装置，船舶的响应情况均与无消浪装置的工况几乎没有差别，也即消浪装置的装载对船舶的响应情况几乎没有影响。

2）本文提出的带有首端和侧壁消浪装置的消浪方案对不同情形的入射波引起的舱内波浪均具有不错的消浪性能。其中，同时装有首端和侧壁消浪装置的情况消浪性能要优于仅有1 种消浪装置的情况，消浪效果达到40%～50%。

3）本文提出的消浪装置方案对舱内波浪的消减主要在首端附近至舱中段的区域效果较为明显，在远离首端的坞舱尾端开口区域效果不明显，并且对波高较高的波浪消浪效果要更加明显。