信用风险、融资费用与初始保证金融资成本

赵胜民,冯美芳

(南开大学 金融学院,天津 300350)

一、引 言

自2007—2009年金融危机以来,交易对手信用风险(Counterparty Credit Risk,CCR)已成为金融机构面临的最大问题和挑战之一。从交易商(dealer)报价的角度来说,交易对手信用风险管理的具体举措是在报价中引入信用价值调整(Credit Valuation Adjustment,CVA),即根据交易对手信用风险收取额外费用。信用价值调整(CVA)是针对交易对手信用风险,对衍生品合约或者衍生品组合的无违约风险价值进行的调整。近年来,由于信贷息差和相关会计(如IFRS13)以及资本要求(巴塞尔协议III)的波动性,CVA已成为衍生品市场的一个关键话题[1]。这意味着,CVA成为不可或缺的要求,因为衍生品价格需要进行调整以反映另一个市场参与者在考虑潜在交易对手风险后的定价。此外,财务会计准则公告《公允价值计量》(FAS157)规定,在按公允价值计量负债的各个时期,报告主体均应考虑其信用状况(信用风险)对负债公允价值的影响[2]。这表明交易方自身的信用风险也应该被视为报价的一部分,这称为债务价值调整(Debt Valuation Adjustment,DVA)。

不完善的信贷市场会出现信贷资源的低效率配置问题[3]。不同于标准化的流动资产(如债券),衍生品市场目前并没有类似的支持回购融资。鉴于暂无可用于再抵押的抵押品,交易者不得不借入无担保资金以满足抵押品要求。这种无担保融资将产生一定的相关成本或费用。融资价值调整(Funding Valuation Adjustment,FVA)是关于衍生品合约中的交易资金(如无担保资金)产生融资费用的估值,无担保衍生品合约的FVA可视为没有信用支持附件(Credit Support Annex,CSA)的成本[4]。从有效贷款和存款的角度解释,FVA是无担保衍生工具产生的有效贷款(存款)的成本(收益)。例如,场外掉期会产生大量的风险敞口,货币内掉期具有类似贷款的特征,货币外掉期具有类似存款的特征。因此,存在一个强有力的论据表明,与贷款一样,衍生品价值中不仅包含交易对手的融资成本,还包含补偿交易对手的融资收益。当然,许多衍生工具既有预期的正风险敞口,也有预期的负风险敞口。因此,不同于贷款和存款,单一衍生工具既可以吸引资金费用,也可以带来收益。初始保证金要求已成为衍生品市场越来越常见的特征。初始保证金需要涵盖任何潜在收尾情况(如结算会员违约)期间交易组合的按市值计价的变动风险。因为在大多数情况下,不允许对初始保证金进行再抵押,因此用作初始保证金的这笔资金需要相应的融资费用,这部分融资费用称为保证金价值调整(Margin Valuation Adjustment,MVA)。撇开技术问题不谈,衍生品部门关心的是如何管理或转移过账初始保证金的额外成本。初始保证金涉及的融资成本通常会通过衍生品定价转移到客户方。

多重价值调整模型是对衍生品交易合约价值中嵌入的信用风险、融资费用及初始保证金融资成本等组成部分的估值。新冠疫情后,金融市场风险传染网络越发紧密[5]。系统地研究这些价值调整,加强金融风险管理,已经变得十分迫切。在实际金融市场中,资产价格波动率会随机变化,它可能受到时间、资产价格及其他随机因素的影响,是一个随机变量。由随机波动率模型可知,当波动率由隐含的随机过程生成时,对波动率的刻画具有更好的样本内拟合表现和样本外预测能力。基于随机波动率对于金融市场风险防范与管理的重要性,结合随机波动率模型来研究金融衍生品的多重价值调整问题显得尤为重要。

二、文献综述

在多重价值调整(X Valuation Adjustments,XVAs)理论体系中,多重价值调整模型是对衍生品交易合约价值中嵌入的交易双方信用风险、交易成本、融资费用及资本要求等组成部分进行量化并估值的有效测度。信用价值调整(CVA)和债务价值调整(DVA)是根据交易合约中交易双方的信用风险高低而对其价值作出的调整,也就是对信用风险的市场价格进行估值。融资价值调整(FVA)是对合约中交易资金产生融资费用的估值,而保证金价值调整(MVA)则是对交易合约中初始保证金融资成本的估值[6]。Hull提及了金融衍生品的多重价值调整在衍生品市场中的重要性,并强烈建议在对衍生品定价时,先进行多重价值调整[7]。关于多重价值调整的相关研究,始于20世纪90年代,Duffie等针对不同交易对手的违约风险,构建了关于交易双方违约资产的估值模型[8]。Huge等基于信用评级模型,研究多个代理违约的可违约证券定价问题[9]。这些研究成果为多重价值调整理论体系的研究奠定了基础。Brigo等在双边违约风险的情况下,给出交易对手风险调整的一般无套利价值框架,并介绍利率投资组合的双边信用价值调整(BCVA=CVA+DVA)的方法和公式[10]。尽管融资成本的计提是否应包含在合约价值中存在一定的争议性,但对融资价值调整的研究并未停止。Hull等通过融资价值调整模型对交易合约的融资成本问题进行探讨,指出根据融资价值调整FVA模型对交易合约融资成本的计算对衍生品合约的定价较为重要[11-12]。Smith通过调研发现,在过去几年中,几家作为利率衍生品主要做市商的大型银行在其财务报表中已经计入了融资价值调整(FVA)[13]。Andersen等认为交易商的融资价值调整(FVA)是其股东的债务悬置(overhang)成本。交易商在报价时会根据公允价值进行融资价值调整,从而最大化股东的利益[14]。

Burgard等根据半复制法,研究了信用价值调整与融资价值调整问题[15]。该方法是在同一框架下研究多重价值调整问题,随后在此基础上,Green等扩展了半复制框架,以涵盖初始保证金的融资成本,推导出保证金价值调整(MVA)[16]。Abbate先概述了交易对手信用风险、自身信用风险和融资成本对无抵押金融衍生品合约定价的影响,然后研究信用价值调整(CVA)、债务价值调整(DVA)和融资价值调整(FVA)[17]。

但是,这些价值调整模型是在标的资产服从经典的Black-Scholes模型下进行的[18]。Black-Scholes模型中假设隐含波动率为常数,而在实际的金融市场中,资产价格的波动率不是常数,而是满足一个与资产相关的随机变化过程,即随机波动率。随机波动率是刻画金融市场中的不确定性与风险水平的重要指标,是判断和解释金融市场状态的重要参数。基于此,Hesston以随机波动率为重点提出连续时间波动率的平方根模型,并经过大量实证发现该模型比B-S定价模型更加精准[19]。随机波动率模型源自经典的Black-Scholes模型,Scott、Wiggins、Renault和Fouque等人基于随机分析理论的发展将其进行推广[20-23]。基于随机波动率模型的重要性,许多学者将其广泛地应用于各种领域,特别是衍生工具的定价。李亚茹等结合随机波动率模型,设计“基于现货市场的价格指数保险+对冲部分风险的场外看跌期权+场内期货”的农产品期货价格保险,并对农产品期货价格保险进行定价[24]。李坤昊等基于平稳仿射随机波动率模型,在仅存有限个期权合约时,根据实际期权价格曲面,使用粒子滤波方法估计瞬时方差,并且,在固定参数条件下,更新Hull-White扩展模型;进一步,利用向前特征过程,推导出下一时刻的期权定价模型[25]。杨璐等研究了Heston随机波动模型下两个投资人之间的随机微分投资组合博弈问题[26]。Catania引入了一种新的随机波动率模型,假设在不同的时间滞后下,测量的冲击数与波动率方程的震荡之间存在一般相关结构,由此推导出的预测结果能够更好地表现出金融时间序列中的杠杆效应和传播效应[27]。

因此,基于已有文献在理论和方法上的启发,将结合随机波动率模型,研究金融衍生品的多重价值调整。本文可能的贡献有:第一,相比以往的多重价值调整模型,考虑了随机波动率这个重要因素,通过金融衍生品的多重价值调整模型,研究了信用风险、融资费用及初始保证金成本的管理问题。第二,通过结果对比分析,相较于布朗运动下的多重价值调整模型,在考虑波动率风险因素后,多重价值调整变化的波动性增大,表明随机波动率对衍生品多重价值调整具有显著的影响。

三、基本假设

(一)金融衍生品的经济价值

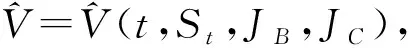
(1)

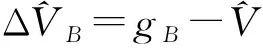
令V(t,S)=M(t,S)(衍生品的按市值计价值),当银行或交易对手违约时,该头寸的平仓或索赔数额通常由衍生工具的按市价计价值决定;当银行或者其交易对手发生违约时,有:

(2)

(3)

其中,gB(V,X)=[V(t,S)-X(t)]++RB[V(t,S)-X(t)]-+X(t)和gC(V,X)=RC[V(t,S)-X(t)]+-[V(t,S)-X(t)]-+X(t),X(t)表示交易初期缴纳的抵押资金,以弥补违约造成的损失。RB为银行的违约回收率,代表银行发生违约后可收回余款的程度;RC为交易对手的违约回收率,代表交易对手违约后可收回余款的程度。

(二)投资组合中资产的价格过程

为了更好地描述资产的价格行为,捕捉资产价格的波动率风险对金融衍生品多重价值调整的影响,将资产价格波动率设为与价格相关的随机过程,即随机波动率模型。Heston模型是通过严格的理论证明得到的期权价格半显性解的随机波动率模型,并且对标的资产和随机波动率的假设是符合金融市场中的实际数据特征。更重要的是,该模型比其他的随机波动率模型容易实现,因此本文选取了Heston模型来刻画资产的价格过程。在随机波动率模型中,标的资产价格St及波动率Yt满足如下的随机微分方程:

(4)

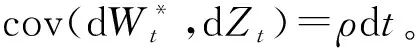
(5)

假设债券P1和债券P2是由银行自身发行的收益率分别为r1和r2的不同等级债券。不同等级且不同回收率的债券不仅能使得投资组合有固定收益,同时也为投资组合提供一定的安全性保障。假设交易对手的债券PC,回收率为RC。债券价格满足的动态方程如下:

(6)

其中,R1和R2为债券P1和债券P2的回收率,且r1-r=(1-R1)λB,r2-r=(1-R2)λB,λC=rC-qC。并且设定银行发行不同等级债券的利差为λB,代表银行违约的危险率,λC为交易对手的违约对冲头寸的有效利率,代表交易对手的危险率。r为无风险利率,债券PC的收益率和借款利率分别为rC和qC。

四、对冲投资组合与合约价值的偏微分方程

(一)对冲投资组合的构建

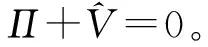
Π(t)=αSS(t)+α1P1(t)+α2P2(t)+αCPC(t)+βC(t)+βS(t)+αXX(t)

(7)

其中,{αS,α1,α2,αC,αX}表示对应资产的投资份额,称为投资策略。对冲投资组合中的抵押账户αXX(t)=αX1X1(t)+αX2X2(t)。设Vt(Π)是投资组合Π在时刻t的值(或称财富,简化为Πt),则:

Πt=αSSt+α1P1+α2P2+αCPC+βC+βS+αX1X1+αX2X2

(8)

在连续时间情况下,投资组合的微分形式如下:

dΠt=αSdS+α1dP1+α2dP2+αCdPC+dβC+dβS+αX1dX1(t)+αX2dX2(t)

(9)

投资组合中含有不同回收率(R1≠R2)的债券是为了抵消衍生品的资产负债表影响。此外投资组合中也会含有供给债券PC的对应现金账户βC和资产价格S的回购账户βS,以债券PC作为抵押的回购账户βC及资产价格S的回购账户βS满足动态方程:

dβC=-αCqCPCdt

(10)

dβS=φ(γS-qS)Sdt

(11)

其中,qS表示确定标的资产股息收益率,γS=r+sβ,S,sβ,S表示超过无风险收益率r的价差。且标的资产与债券各自满足资产约束条件αSSt+βS=0与αCPC+βC=0。

值得说明的是,与现有文献不同,为转移标的资产的波动率风险,本文在对冲组合中加入一个与标的资产相关的未定权益X1=X1(t,St)及关于第三方的固定收益债券X2(t)作为抵押账户。当标的资产的价格过程遵循随机波动率模型(4)时,根据伊藤引理,可得X1=X1(t,St)的微分方程如下:

(12)

X2(t)满足的微分方程如下:

dX2=rX2dt+σX2dZt

(13)

(二)随机波动率模型下金融衍生品的价值过程

在这一节中,基于上述假设条件,根据衍生品合约的价值过程与随机波动率模型下的对冲投资组合,推导出随机波动率模型下金融衍生品的价值过程所满足的偏微分方程。

(14)

证明:根据式(1)给出的衍生品合约价值过程及式(9)给出的对冲投资组合的微分形式,可知:

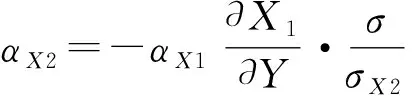
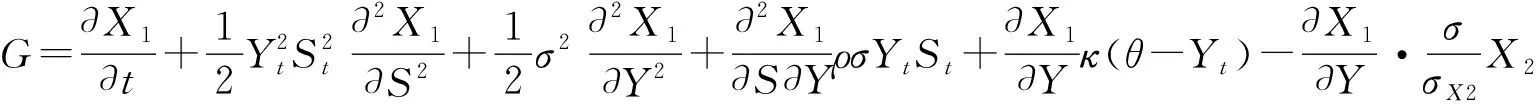
其中,P=α1P1+α2P2,PD=α1R1P1+α2R2P2。

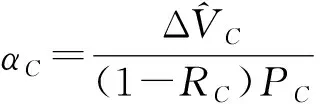
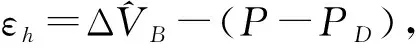
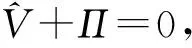
由于采取的对冲投资组合策略是自融资形式,因此漂移项为零,即:

假设该衍生品交易合约在所有情况下复制最终收益H(S),即在T时刻的价值为:

五、随机波动率下金融衍生品的多重价值调整模型

(一)模型求解

(15)

其中,U表示金融衍生品的多重价值调整,它包含了衍生品合约价值中嵌入的信用风险、交易资金产生的融资成本及初始保证金融资成本等组成部分的估值。

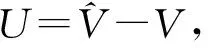
定理2 在标的资产价格服从随机波动率模型的假设下,金融衍生品合约的多重价值调整U满足如下的偏微分方程:

(16)

且多重价值调整模型U为:

(17)

证明:根据定理1结论:

及该交易合约的无违约风险价值V满足标准Black-Scholes偏微分方程:

结合式(15),故总的多重价值调整U满足偏微分方程:

根据Feynman-Kac公式,解得多重价值调整模型U(t,S)为:

证毕。

根据定理的结论,可以将金融衍生品的多重价值调整模型U(t,S)分解为信用价值调整(CVA)、债务价值调整(DVA)、融资价值调整(FVA)及保证金价值调整(MVA)四个模型,具体如下:

(18)

(19)

(20)

(21)

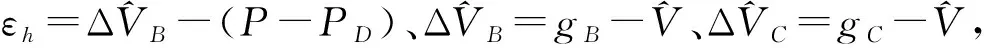
gB=[V(t,S)-(αX1X1(t)+αX2X2(t))]++RB[V(t,S)-(αX1X1(t)+αX2X2(t))]-+(αX1X1(t)+

αX2X2(t))

gC=RC[V(t,S)-(αX1X1(t)+αX2X2(t))]+-[V(t,S)-(αX1X1(t)+αX2X2(t))]-+(αX1X1(t)+

αX2X2(t))

信用价值调整(CVA)模型(18)是银行所估计的由于交易对手违约所引起的预期费用现值。投资银行通常会用CVA来量化评估场外衍生品交易对手预期违约损失值,反映了交易一方对另一方违约风险及由此造成的损失量的估计。与之对应的是债务价值调整(DVA)模型(19),指由于银行自身违约可能给自己带来的预期受益价值贴现值。因为银行本身也可能违约,从而会给交易对手带来损失,损失量为银行的受益价值。信用价值调整模型和债务价值调整模型是刻画交易双方面临的信用风险的度量模型。融资价值调整(FVA)模型(20)是关于衍生品交易中涉及相关融资成本的预期费用现值。保证金价值调整(MVA)模型(21)是对于衍生品合约中关于初始保证金融资费用的价值调整,这里是关于固定收益债券的预期费用现值。对于一份未清算的衍生品交易合约,不管是清算委托书,还是双边担保品规则都会要求进行大量的初始保证金过账。而保证金价值调整模型是针对初始保证金和任何其他如流动性要求过度抵押时产生的成本量化。

(二)模型结果与数值实验

为了对比分析随机波动率模型下金融衍生品的多重价值调整,列出现有文献中的多重价值调整模型[15]。

当标的资产的价格设为布朗运动dSt=μStdt+σStdWt时,建立对冲投资组合Π=δS+α1P1+α2P2+αCPC+βS+βC+X。多重价值调整模型为:

(22)

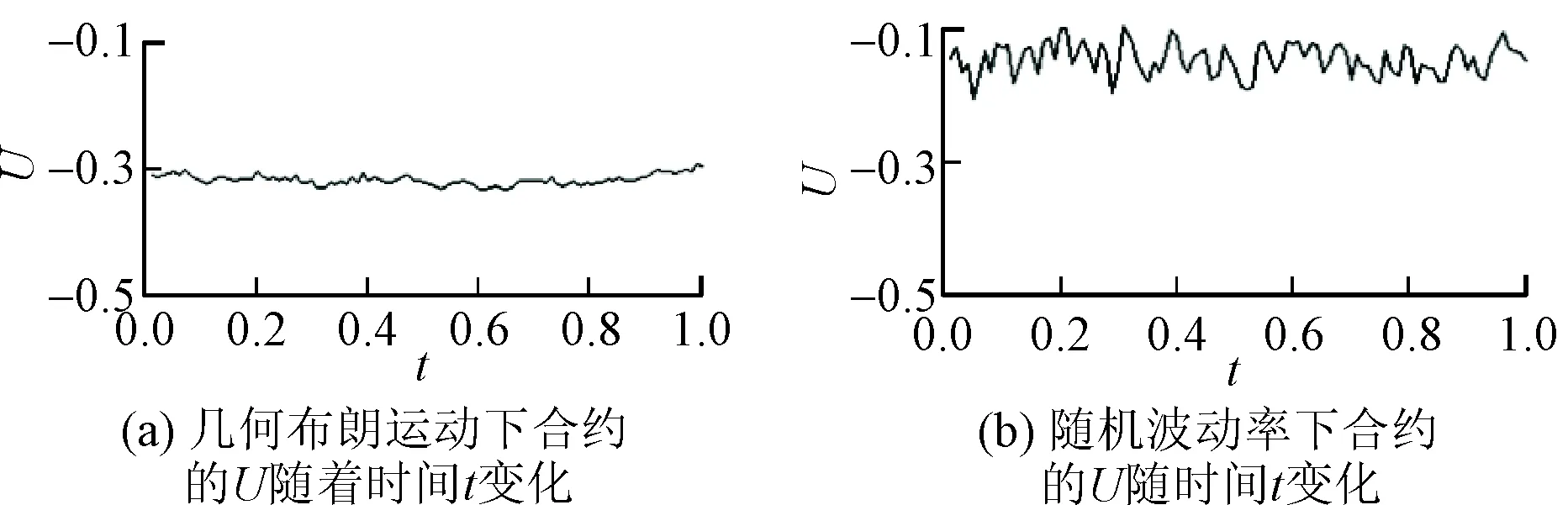
该模型的假设前提是,标的资产价格服从几何布朗运动,并未考虑资产价格的随机波动率。为了使模型能够涵盖这一风险因素,本文在资产动态方程假设中将标的资产的价格过程设为随机波动率模型,得到定理2的结论。理论上而言,随机波动率下的多重价值调整模型(17)比模型(22)更能反映真实的市场情况,是一个更为精确的多重价值调整模型。并且,对比模型(17)与模型(22)发现,由于标的资产价格过程的假设不同,导致模型结果中的按时计价的gC,gB,εh均不同,从而信用价值调整、债务价值调整、融资价值调整及保证金价值调整的计算结果也不同。此外,由于对冲投资组合策略及组合中资产价格过程有所不同,对应保证金价值调整(MVA)明显不同,这表明资产价格波动率风险对多重价值调整具有显著影响。基于实际金融市场中波动率风险是实时存在的风险,结合随机波动率模型研究衍生品合约价值评估与定价的偏差问题更为合理。越精确的多重价值调整模型,越能准确地计算衍生品交易中信用风险的市场价格、合约中涉及的融资费用及初始保证金成本等风险,为交易者调整报价及确定衍生品的公平价格提供更强的理论支撑。

数值实验1考虑一份1年到期、标的资产为股票的衍生品交易合约,假设当前股票价格为100元,股票价格的年波动率为40%,执行价格为110元,无风险利率为5%。不同等级的债券P1和P2,其利率与回收率成反比,利率高的债券回收率低,即当r1>r2时,R1

表1 基于随机波动率模型下金融衍生产品多重价值调整模型参数

基于上述参数设定,根据随机波动率模型下的多重价值调整模型(17),金融衍生品多重价值调整(U)占合约价值的比重为0.016 76;根据随机波动率模型下的信用价值调整模型(18),金融衍生品的信用价值调整(CVA)占合约价值的比重为0.123 05;根据随机波动率模型下的债务价值调整模型(19),金融衍生品的债务价值调整(DVA)占合约价值的比重为0.119 07;根据随机波动率模型下的融资价值调整模型(20),金融衍生品的融资价值调整(FVA)占合约价值的比重为0.027 27;根据随机波动率模型下的保证金价值调整模型(21),金融衍生品的保证金价值调整(MVA)占合约价值的比重为0.005 19。具体如表2。

表2 在布朗运动和随机波动率模型下,CVA、DVA、FVA及MVA占合约价值的比重

对于一个金融衍生品交易合约,在资产价格服从随机波动率模型的假设下,根据多重价值调整模型估算,衍生品交易合约价值中嵌入的信用风险、融资费用及初始保证金成本等风险因素的市场价格占到合约无违约风险价值的1.676%左右,其中金融衍生品的信用价值调整额度占到合约无风险价值的12.305%左右;债务价值调整额度占到合约无风险价值的11.907%左右;融资价值调整额度占到合约无风险价值的2.727%左右;保证金价值调整额度占到合约无风险价值的0.519%左右。这说明对于一份无风险的市场价值为100万元的交易合约,银行基于对交易对手风险与交易费用的评估与计算,根据合约的经济价值给出的报价会高于100万元,假设报价为120万元,至少会包含15.5万元的价差空间(2)由于多重价值调整理论体系中除了信用价值调整、债务价值调整、融资价值调整及保证金价值调整,同时也包含其他价值调整,如资本价值调整、税务价值调整等,所以这里报价高于V+U。(CVA+FVA+MVA),对于交易对手而言,债务价值调整是银行的信用风险,也应该纳入考虑中,即(-DVA)。也就是说,这里的多重价值调整U=1.676万元(CVA-DVA+FVA+MVA),这份合约中包含的信用风险、交易成本及合约融资费用等成本为1.676万元。从表2可以看出,标的资产价格的波动率风险是影响金融衍生品多重价值调整的重要因素。特别是对信用风险的冲击效应,信用价值调整与债务价值调整是交易双方在同一份合约下的信用风险,对比几何布朗运动,随机波动率模型下的信用价值调整模型与债务价值调整模型所估计的信用风险增大。这表明资产价格的波动率风险是影响衍生品信用风险的重要因素。而根据融资价值调整模型估计的交易有效期内的交易成本相对减小,这主要是因为,在考虑随机波动率这个风险因素后,可以避免合约价值的过分高估。最后,初始保证金融资费用增大,是由于在考虑了资产价格的波动率风险后,市场的不确定性增加,导致交易双方违约概率增大,那么需要缴纳的初始保证金可能会增加,进一步初始保证金的融资费用也就增加了。

此外,为了进一步表明随机波动率下的多重价值调整模型的优越性,相应地给出金融衍生品的信用价值调整、债务价值调整、融资价值调整及保证金价值调整随时间的变化过程。

图1和图2为标的资产价格过程服从布朗运动和随机波动率模型两种假设下,信用价值调整、债务价值调整、融资价值调整及保证金价值调整的变化情况。可以看出,考虑波动率风险的情况下,信用价值调整模型与债务价值调整模型所估计的信用风险增大,波动性增大。这主要是因为,资产价格波动率的随机性,体现了市场的不确定性。因此,相较于布朗运动下的多重价值调整模型,当资产价格的波动率假设为随机波动率模型时,对比图1和图2,可以看出,在交易有效期内,度量信用风险的信用价值调整值与债务价值调整值增大,并且波动性上升。同样,在考虑了资产价格的波动率风险后,在交易期内,交易成本的波动性增大,从图2中可以看到,融资价值调整值变化的波动性也增大。此外,对比布朗运动下的保证金价值调整变化,在资产价格波动率风险的影响下,保证金价值调整值增大。这可能是由于,考虑波动率风险之后,初始保证金比例有所提高,初始保证金的融资成本也相应增加。

图1 几何布朗运动下CVA、DVA、FVA及MVA随时间t变化

图2 随机波动率下CVA、DVA、FVA及MVA随时间t变化

此外,相应的参数设定后,根据布朗运动与随机波动率模型下的多重价值调整模型,给出金融衍生品合约多重价值调整U随时间的变化过程,图3为资产价格过程服从布朗运动和随机波动率模型两种假设下多重价值调整的变化情况。结果表明,考虑资产价格的波动率风险后,金融衍生品多重价值调整的波动性显著增大。这主要是由于资产价格波动对交易双方的信用风险冲击较大,进而导致金融衍生品定价出现较大的波动性。通过对比,图3较好地解释了资产价格的波动率风险对金融衍生品多重价值调整的影响。

图3 多重价值调整分别在布朗运动和随机波动率模型下随时间的变化

整体而言,通过对比分析,相较于布朗运动下的多重价值调整模型,在考虑随机波动率这个风险因素后,多重价值调整变化的波动性显著增大,这表明随机波动率对衍生品多重价值调整具有显著影响。首先,金融衍生品的信用价值调整与债务价值调整均增大,表明资产价格的波动率风险会导致衍生品信用风险的市场价格增大;其次,融资价值调整减少,表明交易有效期内的交易成本相对减小;最后,根据保证金价值调整模型估计的初始保证金融资费用增大。这是由于在考虑了资产价格的波动率风险后,市场的不确定性增加,导致初始保证金的融资费用增加。综上,考虑资产价格波动率风险的多重价值调整模型,对金融衍生品价值中嵌入的信用风险、融资费用及初始保证金成本等组成部分的估值更为合理。

六、结论与建议

本文基于随机波动率模型,通过金融衍生品的多重价值调整模型,研究交易合约嵌入的信用风险、融资费用及初始保证金成本等组成部分的估值问题。首先,在标的资产价格过程满足随机波动率模型前提下,构建衍生品交易合约的对冲投资组合;其次,利用对冲原理,推导出金融衍生合约多重价值调整的偏微分方程;最后,运用Feynman-Kac公式,推导出金融衍生品交易合约的多重价值调整模型。根据分解出的信用价值调整模型、债务价值调整模型、融资价值调整模型及保证金价值调整模型,讨论了资产价格波动率风险对金融衍生品交易合约价值中嵌入的信用风险、融资费用及初始保证金成本等组成部分估值的影响。研究结果表明,加入随机波动率使得结论中的多重价值调整模型,能更好地刻画衍生品的信用风险、融资费用及初始保证金成本等风险。进一步对比分析发现,资产价格的波动率风险是衍生品定价偏差的重要影响因素,相较于布朗运动下的多重价值调整模型,随机波动率下的多重价值调整模型可以捕捉到波动率风险对金融衍生品信用风险的影响。所以结合波动率风险的多重价值调整模型是更为贴近实际市场数据,对金融衍生品合约价值中嵌入的信用风险、融资费用及初始保证金成本等组成部分的合理估值。根据本文的研究结论,提出如下几点建议:

第一,多重价值调整理论是研究衍生品合约定价及风险管理的关键,多重价值调整模型有助于提高衍生品定价的精确性。做市商利用定价模型对衍生品进行定价,并结合多重价值调整模型对交易对手信用风险、合约的交易成本等风险进行评估之后,对价格进行调整并给出合理报价。

第二,投资者可根据多重价值调整理论评估衍生品合约价值并理性决策。由于投资者有限理性和专业能力及投资理念较差,投机心理较强,需要相关定价与投资理论指导。投资者在进行交易前,可以根据多重价值调整模型对信用风险的估值大小进行判定,有助于高效规避风险,为投资者提供投资策略的选择依据。

第三,监管部门根据多重价值调整理论完善监管框架,优化监管资本要求。合理的资本要求是经济稳健运行的关键,资本要求过高,降低交易流动性;资本要求过低,增加交易对手风险。不合理的资产监管要求,会扭曲资本金配置。因此,优化监管制度一直是监管层亟待解决的问题。监管部门在制定风险资本金要求,可参考多重价值调整理论建立合理的资本缓冲,从而有效控制交易对手风险。