基于非抽样形态小波的图像融合方法
杨秀林,陈 曦,曹 科,秦国瑾
(四川九洲北斗导航与位置服务有限公司技术中心,成都 610000)
图像融合是通过某种融合系统,将2 个或多个互补的波段、传感器的有用信息综合成统一图像或综合图像特征以供观察或进一步处理,达到对目标或场景更为精确、全面的识别、分析和判决的图像处理方法。
目前图像融合的热点主要是基于多尺度变换的融合[1-3],其通过多尺度分解得到图像的低频信息,并提取图像在多个尺度上的细节(高频)信息。基于多尺度变换图像融合主要是采用小波、超小波、形态小波等进行变换,针对低频信息、高频信息表示的不同物理意义,分别进行融合。
目前,非抽样形态小波在一维信号特征提取中很普遍,例如,文献[4]将其用于主减速器振动特征提取,文献[5]将其用于轮对轴承复合故障信号检测,文献[6]结合形态非抽样小波与DCT 高阶奇异熵来提取液压泵退化特征信号。近年来,基于非抽样形态小波的图像融合研究也取得了一定的研究成果,例如,文献[7]将非抽样形态小波变换应用于图像融合,并提出了将膨胀腐蚀的平均作为分析算子,但是显著目标附近出现了边缘增厚的现象。文献[8]提出了一种S-变换的非抽样形态小波并用于多种类型的图像融合,该形态小波是二维四通道的,通过增加通道和引入增强效果,提高图像融合效果。非抽样形态小波从一维信号特征提取拓展到图像处理应用,从双通道拓展到多通道,特征提取能力逐步增强。
1 相关研究
1.1 形态学图像处理
在生物学中,形态学[9-10]常用来研究动、植物形态和结构,已形成了一个较完善的学科;在数字图像处理中,形态学被用来提取可表达某种区域形状(连通分量、边界、骨架等)的图像分量。数学形态学中,图像被看作是一个大的集合,图像中不同的对象被看作是小的集合,形态学就是采用不同的形态算子提取对图像处理有用的集合。
膨胀和腐蚀在形态学中简单而重要,因为其他的算子都是在其基础上变化而来。设A和B是z2 中的集合,A被B膨胀定义为
式中:先对B取补运算,并保证B的补集中至少有一个值是属于A的,以z进行位移,所有位移后的值就是A被B膨胀的结果。B被称为结构元素,其尺寸与形状具有重要的物理含义,可针对不同的图像处理任务来选择合适的结构元素,常使用方形的结构元素、圆盘的结构元素和钻石形的结构元素等。集合B腐蚀集合A的定义为
式中:点z是B中包含于A中的点之一,平移所有这样的z点得到的值就是腐蚀的结果。A腐蚀B结果的补集等于A的补集膨胀B的反射,如下所示
开运算和闭运算被膨胀运算和腐蚀运算的组合所定义。在处理过程中,图像中的对象往往被膨胀运算所扩大,图像中的对象往往被腐蚀运算所侵蚀缩小。图像中狭窄的间断和细的突出物往往被开运算所断开和消除,所得的轮廓变得平滑;狭窄的间断、细长的鸿沟、小的空洞往往会被闭运算所消除,轮廓线中的断裂往往会被闭运算所填补,轮廓线变得更加光滑。开运算和闭运算的结果都让图像的轮廓变得平滑,但意义和效果不一样。开运算定义为
开运算就是B先腐蚀后膨胀A,闭运算就是B先膨胀后腐蚀A,闭运算定义为
与二值图像处理相比,灰度图像的处理更加普遍。现在介绍灰度图像的形态学处理。假设f(x,y)是输入图像,b(x,y)是结构元素,它们都是离散的表达形式,图像f的灰度级是整数且是以二维坐标(x,y)的灰度值函数。结构元素b膨胀灰度图像f定义为
Df是输入图像f的定义域,Db是结构元素b的定义域。位移量x和y必须在结构元素b的定义域内,(s-x)和(t-y)必须在f的定义域内。灰度膨胀使用最大值运算来取代二维卷积的求和运算,使用加法运算来取代二维卷积的乘积运算。灰度腐蚀定义为
类似地,位移量x和y必须在b的定义域内,(s+x)和(t+y)必须在f的定义域内。灰度腐蚀使用“最小值”运算来替代灰度膨胀的“最大值”运算,使用减法运算来替代加法运算。灰度膨胀和腐蚀比二维卷积运算计算速度快。灰度图像的膨胀运算和腐蚀运算也是关于函数求补和映射相关相互对偶的。
灰度开运算定义为
灰度闭运算定义为
灰度开运算和闭运算同样是关于函数求补和映射相关对偶的,关系为
图像处理中,灰度开运算先灰度腐蚀后灰度膨胀,灰度腐蚀去除了微小的图像细节使其有所变暗;灰度膨胀使图像整体亮度增强,但是灰度腐蚀去除的细节不被再引入了。灰度闭运算先灰度膨胀后灰度腐蚀,灰度膨胀去除了图像中的暗细节并使其亮度增强;灰度腐蚀不会使去除的信息再引入。灰度开运算常用来去除小而亮的图像细节并保持整体灰度级和明亮区域相对不变。灰度闭运算常用来去除图像中较小而暗的细节并保持明亮部分相对不变。
1.2 高帽变换
1.1 节中依次介绍了二值形态学、灰度形态学的基本操作:膨胀、腐蚀、开运算和闭运算。开运算和闭运算被膨胀和腐蚀的组合操作所定义,高帽变换被开运算和闭运算所定义。高帽(Top Hat) 变换包括白帽(White Hat)变换和黑帽(Black Hat)变换。假设灰度图像和结构元素分别为A和B,白帽变换和黑帽变换定义为
由式(11)、(12)可以看出,白帽变换是由原图与经过开运算结果的差值运算得来的,黑帽变换是由原图与经过闭运算结果的差值运算得来的。开运算或闭运算不具有自对偶性。开运算可以平滑图像亮的特征,因此,白帽变换可以提取图像的亮细节(尖峰信号)[11];闭运算可以平滑图像暗的特征,因此,黑帽变换可以提取图像的暗细节(低谷信号)[11]。如果在图像处理中同时采用白帽变换和黑帽变换来提取不同的细节信号、进行分别的处理,那么通过互补原理就可以对信号进行更好的分析。
1.3 非抽样形态小波的一般框架
与线性尺度空间相比,非线性尺度空间能更好地描述图像的性质,图像被多尺度分解后依然能更好地保持边缘等重要的物理特性。形态小波应用于图像融合虽然具有非线性、计算实现简单的优点,但是下采样会产生吉布斯效应,通常只分解1 层,分解2 层以上均不能取得好地融合效果。文献[12]提出了一种构造非抽样形态小波的基本方法并定义为
式中:id为等同算子,φj为第j个尺度上的尺度分析算子,ωj是第j个尺度的细节分析算子;ψj是第j个尺度上的综合算子。使用T()来表示形态学算子,可根据实际需求选择基本算子或组合使用某些算子。在这个框架下,研究者提出了多种非抽样形态小波的构造方法,例如,文献[4]在主减速器振动特征提取过程中,采用开闭级联的分析算子来构造UMW,分析算子为
式中:n为信号分解的尺度,尺度j+1 上的低频信号yj+1 等于分别对尺度j上的信号xj进行开运算和闭运算所得结果的平均,尺度j+1 上的细节信号yj+1等于xj与xj+1两者之差。由于开运算和闭运算具有幂等性,研究中采用了大小随尺度递增的结构元素,Bn的定义为
文献[8]提出了采用膨胀与腐蚀的平均作为分析算子,记为DE-UMW,并用于图像融合,获得了不错的融合效果,如式(16)所示
式中:n为信号分解的尺度,尺度j+1 上的低频信号xj+1等于分别对尺度j上的信号xj进行膨胀和腐蚀所得结果的平均,尺度j+1 上的细节信号yj+1等于xj与xj+1两者之差。为了增大尺度之间的差异性,该文中也采用了大小随尺度递增的结构元素。由上面的讨论可以知道,非抽样形态小波的框架比较简单,有优良的尺度特性和非常快的分解和重构速度,在图像融合方面具有潜在的优势。
2 基于非抽样形态小波的图像融合方法
2.1 三通道的形态非抽样小波
由前面的知识可以知道,UMW 实际上是用数学形态学算子构成的非线性滤波器T()来替代不可分离àtrous小波变换中的低通滤波器hi,和àtrous 小波一样是二维双通道的。UMW 变换和反变换的流程图如图1 所示。

图1 UMW 变换与反变换过程
在图像融合中,采用DE-UMW 取得的融合效果较好,但是其不能很好地满足形态学尺度空间的局部极值保持和缩减的空间属性[8]。本文仔细分析了UMW 的表达形式,从另外一个角度来构造新的UMW。DEUMW 方法采用腐蚀与膨胀的平均作为UMW 的分析算子,如公式(17)—(19)所示。
公式(17)表示尺度j+1 上的低频图像,式(18)表示尺度j+1 上的细节图像,式(19)表示由低频图像和细节图像重构回上一个尺度的图像。可以看出,细节图像中的系数相当于某种意义上的梯度算子,即一种导数方向可以自适应改变的二阶导数。这种自适应改变的梯度使输入图像中灰度级的阶跃变得更为剧烈,这与提高融合图像与源图像的相似程度是不相符的。因此,本节将细节信号中的二阶梯度进行拆分,分解为2 个一阶的梯度,该方法记为DE-3CUMW,如公式(20)—(23)所示。
式中:低频图像较DE-UMW 方法没有任何改变,如公式(20)所示。细节信号分解为某种程度上的一阶梯度的形式,如公式(21)、(22)所示。显然,一阶梯度不会使输入图像的灰度阶跃像二阶梯度那样剧烈。公式(23)将低频图像和细节图像重构回上一个尺度的图像。
本节给出了3CUMW 分解与重构过程如图2 所示,采用了3 个分析滤波器T、T1 和T2,增加了1 个通道的存储空间,且较UMW 方法增加了1 次加法、1 次减法和1 次除法运算。

图2 三通道的非抽样形态小波变换分解与重构过程
如果采用开闭运算的平均作为非抽样形态小波的分析算子,记为OC-UMW,将其拓展为三通道的非抽样形态小波,记为OC-3CUMW,如公式(24)—(27)所示。
注意,公式(25)是多尺度白帽变换,公式(26)是多尺度黑帽变换。同样,低频图像和原来一样。细节图像分解为2 个细节图像:由白帽变换提取的亮细节(尖峰信号)图像;由黑帽变换提取的暗细节(低谷信号)图像。细节图像中既有亮细节又有暗细节,在融合时就更有针对性了。因为结构元素对增强阴影的细节很有用处[10],所以OC-3CUMW 采用圆形的结构元素。
2.2 实验步骤
本节将DE-3CUMW 和OC-3CUMW 两种方法应用于图像融合,并与DE-UMW 和OC-UMW 进行对比,使用1 组红外线和微光图像,1 组多聚焦图像和1组不同季节的遥感图像进行实验,实验过程如下:第一步分解源图像,得到相应的低频图像和各个尺度上的细节图像;第二步融合系数,将分解所得的低频加权平均,所得的高频选择绝对值较大的系数;第三步反变换,将融合后的低频系数与高频系数进行UMW 反变换以获得融合图像。为了进行公平的比较,除3CUMW 分解2 层外,各种方法都采用5 层分解;OC-3CUMW 使用圆形的结构元素,其他方法使用方形的结构元素,所有的结构元素递增以增加各个尺度之间的差异。
3 实验及分析
本节使用信息熵EN、互信息MI、平均梯度AvG、边缘保持度Qabf 和结构相似度SSIM[9]等客观指标来评价融合图像。
3.1 红外可见光图像融合
本节使用一组像素为632×496 的红外和可见光图像,源图像和各方法的融合结果如图3 所示。图3(a)是红外图像,图3(b)是可见光图像。图3(c)中的显著目标出现了边缘增厚的现象,图3(d)情况类似;图3(f)较图3(e)更清晰,视觉效果更好。

图3 红外可见光图像融合结果
与各方法的融合结果相对应的评价指标见表1。
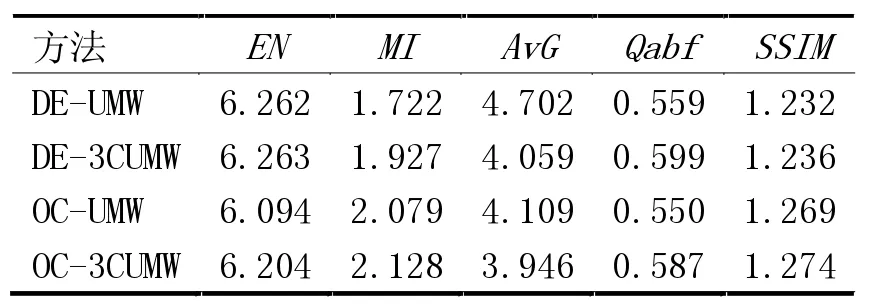
表1 红外与可见光图像的融合客观评价指标
计算表1 所得的数据发现,DE-3CUMW 比DEUMW 的平均梯度下降13.7%,信息熵增加了,度量图像相似度的MI、Qabf 和SSIM 相应增加了。较OCUMW 方法,OC-3CUMW 方法的融合图像平均梯度降低了4%,信息熵有所增加,度量图像相似度的MI、Qabf 和SSIM 相应增加了。DE-3CUMW 方法有3 个指标优于OC-3CUMW,但存在边缘增厚的现象。综上所述,OC-3CUMW 的融合效果综合评价更好。
3.2 多聚焦图像融合
本节使用一组像素为512×512 的多聚焦图像,源图像和各方法的融合结果如图4 所示,图4(a)是左聚焦图像,图3(b)是右聚焦图像。图4(c)中的显著目标出现了边缘增厚的现象,图4(d)情况类似;图4(f)较图3(e)更清晰,视觉效果更好。

图4 多聚焦图像的融合结果
与各方法的融合结果相对应的评价指标见表2。

表2 多聚焦图像的融合客观评价指标
同样,由表2 的数据计算,DE-3CUMW 比DEUMW 的平均梯度降低了12%,信息熵有所降低,度量图像相似度的MI、Qabf 和SSIM 相应增加了。较OCUMW 方法,OC-3CUMW 方法的融合图像平均梯度降低了5.8%,信息熵有所降低,度量图像相似度的MI、Qabf 和SSIM 相应增加了。OC-3CUMW 方法有4 个指标优于DE-3CUMW,OC-3CUMW 的融合效果综合评价最好。
3.3 遥感图像融合
本节使用一组像素为512×512 的某地区不同季节的遥感图像,源图像和各方法的融合结果相应的评价指标见表3,而融合结果如图5 所示。
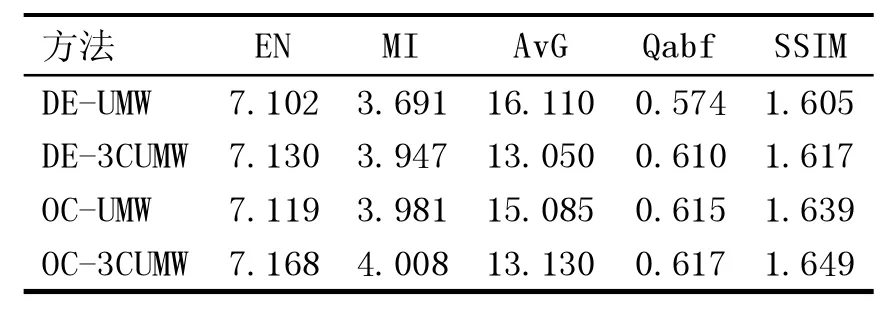
表3 遥感图像的融合客观评价指标

图5 遥感图像的融合结果
类似地,由表3 可以看出,3CUMW 方法的融合图像平均梯度比UMW 方法相应减少了,信息熵有所增加,度量图像相似度的MI、Qabf、SSIM 相应增加了。OC-3CUMW 方法有5 个指标优于DE-3CUMW,OC-3CUMW 的融合效果综合评价最好。
综上所述,DE-3CUMW 与DE-UMW 进行比较,OC-3CUMW 与OC-UMW 进行比较得出以下结论:①由于通道的扩展,需要的存储空间增多;②DE-3CUMW 将二阶的细节形式拆为2 个一阶的形式,降低了融合图像的平均梯度;③融合图像与源图像更加相似且融合效果更佳;④OC-3CUMW 的融合效果最好;⑤三通道的非抽样形态小波适合多种类型的图像融合应用,且计算简单可以用于实时图像融合。
4 结束语
本文提出一种三通道的非抽样形态小波的构造方法,并应用于图像融合。通过红外与可见光图像、多聚焦图像、遥感图像的图像融合实验,证明了该方法的有效性。目前,低频信息融合、高频信息融合采用取均值的方法,研究基于三通道非抽样形态小波变换下低频信息、高频信息的融合策略将是下一步目标。

