隔离开关触头系统电动力计算及仿真
雷 元,陈 程,李 明
应用研究
隔离开关触头系统电动力计算及仿真
雷 元1,陈 程2,李 明2
(1. 武汉船用电力推进装置研究所,武汉 430064;2. 武汉长海电气科技开发有限公司,武汉 430064)
短时耐受能力作为考核隔离开关的一个重要性能指标,电动力的分析至关重要,尤其是大电流下触头系统的电动力分析。本文针对现有的隔离开关触头系统分别采用了理论公式和有限元仿真进行了计算。结果表明该触头系统的电动力满足使用要求,论证了该触头系统的可靠性,为其使用提供了理论依据。本文中的电动力分析同时也验证了霍尔姆力理论计算和仿真的一致性,为后续霍尔姆力分析提供了两种不同方法,对后续研究霍尔姆力具有较大参考意义。
隔离开关 电动力 触头系统 霍尔姆力
0 引言
隔离开关电动力分析对隔离开关至关重要,电动力验算可以判定其结构设计是否合理。在电力系统中,隔离开关作为其中一个元器件,短时耐受能力是考核隔离开关电动力极为重要的性能指标。触头系统做为隔离开关的重要组成部件,其结构设计是否合理直径影响了隔离开关的短时耐受性能,因此对其进行电动力分析非常重要。
触头系统除了受流经整个导体回路中电流所产生的电动力外,还受到动静触头间所产生的霍尔姆力[1]。因为动静触头接触面看起来是平整的、完全接触的,但实际上动静触头接触面是凸凹不平的,接触为点与点接触,这些接触点即为接触斑点。而且接触面不会只在一个接触斑点接触,接触斑点随机不集中。当电流流经这些接触斑点时,电流线会在接触斑点处发生收缩,导致流入流出的电流方向相反,因此动静触头会在接触位置处产生电动斥力即为霍尔姆力[2]。电流越大,霍尔姆力也越大,对触头结构力的影响也就越大,因此大电流下的霍尔姆力分析很重要。
在系统中,如果触头系统电动力过大导致触头系统中动静触头斥开,则会导致隔离开关动静触头处产生电弧,由于此隔离开关属于不带载开关设备,因此会烧蚀隔离开关动静触头,损坏隔离开关设备进而影响整个电力系统。为此,需要对隔离开关触头系统电动力进行计算与分析来判定触头结构设计的合理性,本文中的隔离开关短时耐受电流指标较高,峰值电流130 kA。
1 主回路电动力计算
电动力的产生是因为电流流经导体回路而产生磁场,电流在磁场中所受的力即为电动力。电动力的大小和方向与电流的种类、大小和方向有关,同时也与电流经过的回路形状、回路的相互位置、回路的介质、导体截面形状有关[3]。理论计算电动力时往往采用毕奥—沙伐尔定律和能量平衡原理。
以毕奥—沙伐尔定律为例,当载有电流的导体长度在磁场所产生的电动力可以通过以下式子求出。
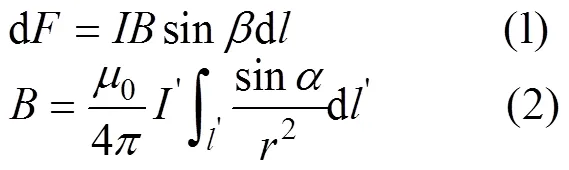

以能量平衡原理为例可求得电动力公式所示。

式中:1、2—两导体自感系数;—两导体间互感系数。
因此只要知道两系统的自感系数及两系统间的互感系数既可以求出电动力。
药店里的西药感冒药成百上千种,如何选择感冒药常常让人无所适从。事实上,感冒药的品种虽多,但不同品种所含的有效成分大同小异,熟悉这些有效成分比记住感冒药的商品名更重要。西药感冒药里的有效成分无外乎下列5类:①抗过敏成分;②减轻鼻黏膜充血的成分;③解热镇痛抗炎成分;④祛痰成分;⑤镇咳成分。
但在实际过程中通过理论计算电动力往往较复杂且计算偏差较大,因此工程应用中往往通过有限元仿真软件来求解电动力,求解速度快且能满足实际工程需求。本文中则采用仿真软件来计算电动力。隔离开关导体回路主要包含进出铜排、软连接、动触头组件、静触头等组成。经测量动触头组件中动触头片与静触头的压痕约为1 mm,由于动触头片宽度为4 mm,因此动触头片与静触头的视在接触面积为4 mm2,最终简化模型如图1所示。

图1 导体回路简化模型
由于两极回路结构形式一样,且单个动触头组件中动触头片数量为12片呈上下对称分布,因此分析动触头片的电动力则需选择上侧6片即可。上侧动触头片编号如图2所示。

图2 动触头片编号示意图
隔离开关短时耐受电流有效值为100 kA,峰值电流为130 kA,因此实际加载值为130 kA,同时两级为串联形式。对上述简化模型进行仿真求解可以得出整个导体回路的电流密度,具体如图3、图4所示。

图3 导体回路电流密度云图
由电流密度云图可以看出,各个动触头片流经的电流大小一致,动静触头接触位置处电流密度最大。通过仿真软件后处理中的场计算器,根据动触头片的电流密度可以求出每个动触头片上的电流大小。同时也可以求出每个动触头片绕轴的转矩[4]。本文中我们只需求解上侧6个动触头片即可。求解结果如表1所示。

图4 导体电流密度数值图
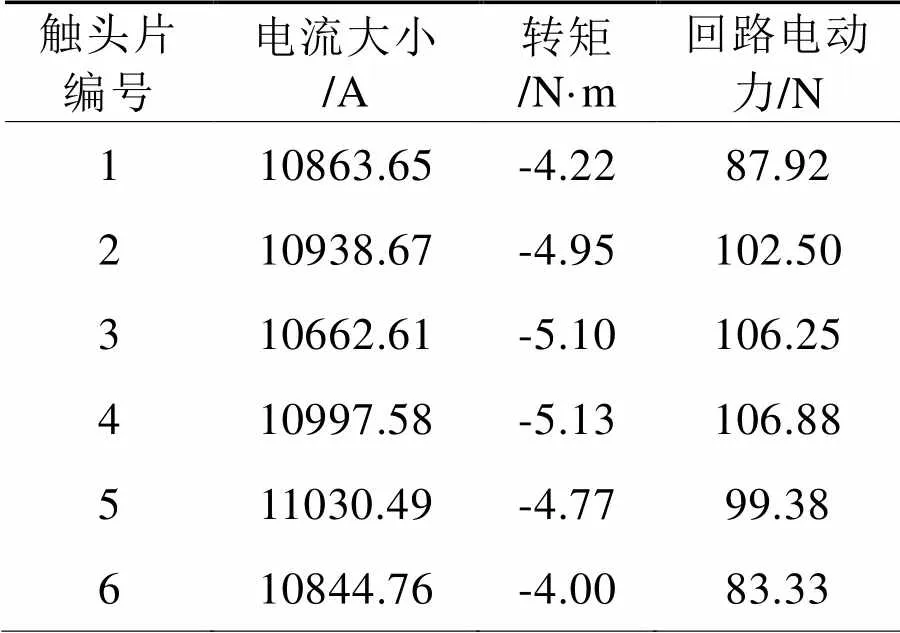
表1 不同动触头片电流及电动力
由上表可以看出,流经每个动触头片的电流大小一致且电动力方向和弹簧压力方向一样,均有利于动静触头压紧。编号6的动触头片电动力最小,也最危险,因此下文将其作为主要分析对象。
2 触头片间霍尔姆力计算
霍尔姆力只存在动静触头接触的过程中, 求解霍尔姆力时往往做如下假设:①接触表面只有一个导电斑点,或把导电斑点集中到中心位置处,使其形成一个大的导电斑点;②导电斑点是一个超导小球,不是一个平面,且此超导小球是一个等位体;③超导小球的电流-电位场是对称分布的,且电阻率处处相等,根据上述假设可以得到一个孤立的导电斑点物理模型[4]。如下图5所示。

图5 导电斑点物理模型
导电斑点超导小球的半径为,圆柱形接触导体的截面半径为,根据导电斑点的物理模型,可以定量分析动静触头间由于电流收缩产生的霍尔姆力,其理论计算公式如下。

式中F—接触处的霍尔姆力;—真空磁导率;流经收缩区的电流;—导电斑点超导小球半径;—圆柱形接触导体截面半径。其中又满足如下公式[5]。

式中—触头接触压力;—材料的布氏硬度;—触头接触面系数。其中触头接触压力包含了弹簧压力、洛伦兹力及霍尔姆力。具体如下所示。
= F+ F+ F(6)
式中F—弹簧压力;F—回路中的洛伦兹力;F—霍尔姆力。因此结合上述三个式子可以得出最终的霍尔姆力公式。

同时根据面积相等原理,R=WL,其中分别为接触面宽和长。因此上述公式可以转化如下。

触头接触压力中,弹簧压力F和洛伦兹力F属同一方向,与霍尔姆力F相反,因此本文中取洛伦兹力最小编号为6的动触头片作为研究对象。式中相关参数取值如下表所示。

表2 霍尔姆力式中相关参数取值
将上述参数值代入式子可得

利用数理软件对上述式子进行迭代运算可求得:F=14.48 N
因此触头的最终接触压力可求得
= F+ F+ F=23.26+83.33-14.48
=92.11 N > 0 N (10)
因此该隔离开关触头系统可靠,能满足实际使用需求。
3 触头片间霍尔姆力仿真
为了仿真求解动静触头接触处的霍尔姆力,需要在原有的简化模型上建立一个导电桥模型。导电桥模型选择圆柱体并建立在动触头片上[6]。
通过式(5)可以求出导电桥半径,通过实际测量接触电阻,可以求出导电桥长度。导电桥半径如下所示。

因此建立的含有导电桥模型如图6所示。

图6 导电桥模型
最后运用仿真软件对上述模型进行仿真,可以求出每个动触头片在霍尔姆力影响下的最终力矩,本文以编号为6的动触头片为分析对象,求解的最终力矩为-3.34 N·m。
将不含导电桥算出的力矩与含导电桥算出的力矩作差即可求出霍尔姆力所产生的力矩。如下所示。
F=-4.00-(-3.34) N·m=-0.66 N·m (12)
根据霍尔姆力力矩进而可以求出霍尔姆力大小如下所示。
F=0.66/0.048=13.75 N (13)
仿真结果和理论计算结果对比如下表所示。

表3 霍尔姆力仿真和理论对比
可以看出仿真结果和理论结果一致,相对误差为-5.04%,仿真结果可信。
4 总结
本文采用有限元仿真软件和传统理论公式相结合的方式,分析了隔离开关触头系统的电动力。验证了该触头系统的可靠性,为实际使用提供了可靠的理论依据。同时对霍尔姆力分别进行了理论计算和有限元仿真,论证了霍尔姆力理论计算和仿真的一致性,为后续霍尔姆力分析提供了参考。
[1] 张敬菽,陈德桂,刘洪武,等. 计及电动斥力效应的低压塑壳断路器机构动力学仿真[J].西安交通大学学报,2004, 38(4): 343-347.
[2] 代颖,刘哲,赵文华.现代低压电器技术[M]. 北京:机械工业出版社,2019.
[3] 许志红.电器理论基础[M]. 北京:机械工业出版社, 2020.
[4] 姚翠平. 小型断路器触头动态仿真及分析[D]. 天津:河北工业大学,2012.
[5] 周安康. 中压真空断路器桥式触头系统电动力分析
[6] [J]. 电器设计与探讨, 2019(13): 35-37, 45.
[7] 陈晋生,迟长春. 直流接触器触头系统电动斥力仿真及优化[J]. 上海电机学院学报, 2021, 24(1): 13-18.
Electrodynamic force calculation and simulation of isolating switch contact system
Lei Yuan1, Chen Cheng2, Li Ming2
(1. Wuhan Institute of Marine Electric Propulsion, Hubei, Wuhan 430064,China; 2. Wuhan Changhai Electrical Technology Development Co., Ltd., Hubei, Wuhan 430064, China)
TM564
A
1003-4862(2023)10-0033-04
2022-12-13
雷元(1987-),男,工程师。研究方向:隔离开关、断路器。E-mail:710469131@qq.com

