陕北黄土高原无资料地区洪水特征值分位数估算方法研究
张洪波, 张靖铷, 夏岩, 丁浩, 邵淑婷, 高文冰
(1.长安大学 水利与环境学院,陕西 西安 710054; 2.长安大学 旱区地下水文与生态效应教育部重点实验室,陕西 西安710054;3.中国石油长庆油田公司勘探开发研究院,陕西 西安710021; 4.低渗透油气田勘探开发国家工程实验室,陕西 西安710021)
受气候变暖影响,近年来全球气候形势日趋复杂,异常气候凸显,极端事件多发,气象灾害频现[1]。已有研究表明,这些极端气候事件带来的风险正不断地从自然物理系统向社会经济系统蔓延,致灾风险日益升高,且已对生态环境和社会经济发展构成了重大威胁[2]。洪水灾害是极端气候事件诱发的主要自然灾害之一。近年来,受极端天气影响,我国洪涝灾害频发,且损失较大,对诸多地区的现代化建设及流域高质量发展产生了极大的危害与影响[3]。特别是对无资料地区,由于观测数据短缺,难以对极端事件的强度及覆盖范围进行准确预估,导致防洪预案与管理措施的科学性不强,“小水大灾”现象时有发生。为了缓解这一问题,许多学者聚焦无资料地区的洪水特征值分位数估算研究[4-7],提出了水文模型、区域频率分析等一系列估算与设计方法,极大地弥补了传统水文手册和水文图集在应用过程中所存在的估算精度偏低的缺陷[6,8-9]。
当前,区域频率分析(regional frequency analysis,RFA)[10]凭借其充分利用相似流域资料扩充信息量,进而有效克服单站样本序列资料短缺局限的优势,已成为解决无资料地区洪水特征值分位数估算问题的重要方法之一。尤其是在一些因影响要素众多、驱动过程复杂而引发空间异质性较大的地区,RFA的优势更为明显。目前,RFA主要包括两个方面[11],即同质区域识别和区域估计。同质区域识别即确定无观测或无资料站点相适合的站点组。当前,相关领域确定同质区的原则与方法主要包括地理相关性[12-13]、主观划分[14-15]、客观划分[16-17]和多变量分析[18-19]等。洪水的形成由于受气候、地形、土壤等条件的综合影响,成因相对复杂且在时间上处于不连续的时变状态,这给原本面临数据短缺问题的目标区域洪水特征值分位数估算带来了更大的挑战。在方法上,同质区域识别多采用多变量分析法,其中以典型相关性分析(canonical correlation analysis,CCA)[20-21]和非线性典型相关性分析(nonlinear canonical correlation analysis,NLCCA)[22-24]最为常见。在区域估计或者说分位数估算方面,也有学者开展了很多深入的研究,提出了一些线性和非线性模型,如多元线性回归(multiple linear regression,MLR)模型[25-26]、广义加性模型(generalized additive model,GAM)[27-28]等,并通过建立解释变量与响应变量之间的函数关系,实现了对洪水特征值分位数的估算。如:陈华等[29]应用区域频率分析法估算了湘江流域衡阳站(假设数据短缺站)的设计洪水,通过与水文比拟法结果的对比,验证了区域频率分析方法在湘江流域的适用性;OUARDA T B M J等[30]分析了CCA与其他技术(层次聚类分析和克里金技术)在同质区域划分方面的集成应用特点,并通过与多元回归区域估计方法的耦合,实现了对区域洪水分位数的定量评价,结果表明CCA具有最佳性能表现;OUALI D等[25]将NLCCA引入区域洪水频率分析中,通过与对数线性回归模型相结合,发现了基于NLCCA的RFA在洪水分位数估计中的有效性;CHEBANA F等[31]采用CCA识别同质区域,采用GAM实施区域估计,并将结果与其他RFA的进行了对比,结果表明,GAM相对灵活,可以表示变量之间的非线性效应,使得基于GAM的RFA模型保有优势。
通过文献梳理发现,尽管区域洪水频率分析方法已经取得了一定的研究进展,并在很多地区取得了很好的应用效果,但是在黄土高原地区的研究尚未开展。众所周知,黄土高原水文站点和气象站点布设稀疏,场次洪水资料和暴雨观测资料序列短且代表性不足,水文设计中常用的洪水频率计算方法和暴雨推求设计洪水方法在黄土高原地区无法应用,亟待寻求更有效的估算手段,解决黄土高原无资料地区设计洪水推估和分位数估算问题。为此,本文对由典型同质区域识别方法和典型水文分位数估算方法组合而成的多种区域洪水频率分析方法展开探讨,并分析其在陕北黄土高原地区的洪水特征值分位数估算中的效能,进而筛选出适用于陕北黄土高原无资料地区洪水特征值分位数估算的最优方法。
1 研究区概况与数据处理
榆林市地处陕北黄土高原,位于陕西、甘肃、宁夏、内蒙古、山西5省份的接壤地带。区域地势大致从西向东、从西北向东南倾斜,海拔为567~1 911 m。榆林市地貌大致分为风沙滩区、黄土丘陵沟壑区和梁状低山丘陵区3类。风沙滩区主要分布在辖区北部,是毛乌素沙漠的南缘,地形起伏不大,但沙丘沙地绵延不断;黄土丘陵沟壑区主要分布在辖区东部,沟壑纵横,梁峁起伏;梁状低山丘陵区主要分布在辖区西南部的白于山地区,地势高亢,梁塬宽广,山大沟深,侵蚀强烈[32]。
榆林市属暖温带和温带半干旱大陆性季风气候,冬寒夏凉,降水量少且分配不均[33],春季多风沙,霜冻时间长。年平均气温7.11~9.94 ℃,年降水量325~474 mm,且年内分布极不均匀,6—9月份降水量占年降水量的75%以上。榆林市雨季常发生暴雨,天气系统一般多为切变线和地槽。由于副热带高压变化较大,冷空气势力强,暖空气势力较弱、冷热空气移动速度快。因此,榆林市多出现短历时小面积暴雨,且以7月和8月份最为多发[34]。榆林市各条河流的洪水,主要由暴雨所形成,暴雨在7—9月出现最多。由于榆林市内覆被率相对较低,雨强大,所以区域洪水突发性强,陡涨陡落,峰形尖瘦,峰高量小。虽总量不大,但“小水大灾”的现象时有发生。同时,受经济发展以及社会基础设施建设水平的影响,榆林市目前的水文气象观测站点密度相对其河网密度较低,观测站数量不足,无资料地区较多。当前,随着气候变化和区域植被覆盖的改善,区域暴雨洪水较以前更为多发,已严重威胁人民生命安全与社会高质量发展。因此,无资料地区的洪水特征值的科学估算问题亟待解决。
为此,本文选取了榆林市境内的28个水文站点(图1)的实测日径流数据,通过统计构建了各站点最大一日流量(maximum daily flow,MDF)的分位数序列,并将其作为各站点的洪水特征值序列,即响应变量序列。尽管最大一日流量不具有较高的时间分辨率,难以准确体现洪峰、洪量和洪水过程,但对于无资料或资料短缺地区无疑是有价值的,在条件允许的情况下亦可通过建立最大一日流量与瞬时洪峰流量的响应关系,开展设计洪水频率分析。

图1 榆林市河流水系及水文站点分布图
各站点的实测径流数据来自黄河水利委员会和陕西省水文局,均为整编数据,具有较好的可靠性和代表性,且均通过了一致性检验。同时,为了有效估算榆林市无资料地区的洪水特征指标分位数,选取气象变量(10个)、人类活动影响变量(1个)和自然地理变量(3个)作为洪水特征指标分位数的解释变量。其中,气象变量包括表征同期降水、气温、风速、湿度、气压等要素的变量,涉及榆林市境内及周边的13个气象站点,数据来源于中国气象数据网;人类活动影响变量指淤地坝控制面积,共涉及2万余座分布于不同流域的淤地坝的相关参数,数据来源于榆林市水利局;自然地理变量包括水文站地理位置、集水面积,数据来源于黄河水利委员会印制的水文数据年鉴。为表述方便,本文将除水文变量(MDF)以外的其他变量统称为物理气象变量。表1列出了榆林市所有选定响应变量和解释变量数据的初步统计结果。

表1 各变量的基本统计参数
为避免解释变量存在数据重叠问题,分别对表1中的洪水特征值与物理气象变量进行两两相关性分析,以实现解释变量的有效筛选。图2是榆林市内洪水特征值分位数和物理气象变量之间的相关性热力图。

图2 不同变量间的相关性热力图
由图2可知:①不同重现期的洪水特征值分位数(Qs5、Qs10、Qs20、Qs50和Qs100)间具有强正相关性。②洪水特征分位数与集水面积(BV)之间具有较强的正相关性,与淤地坝控制面积(CDA)、经度(LONG)、日平均气压(PRES)、日平均相对湿度(HUM)之间呈较弱的正相关性,与日平均风速(WND)、日照时间(SSD)之间呈弱负相关性,与日平均气温(TEM)和日最低气温(MNTM)间的相关性极弱(相关系数趋近于0)。③不同的物理气象变量之间呈现出了差异性的相关性。其中,集水面积(BV)、经度(LONG)与其他物理气象变量之间的相关性最弱;纬度(LAT)、日照时间(SSD)与其他物理气象变量之间多呈负相关;温度、湿度与其他物理气象变量之间多呈正相关。
考虑到物理气象变量中的信息重叠可能影响解释变量与响应变量间的关系构建,结合日平均气温(TEM)和日最低气温(MNTM)与洪水特征值分位数间趋零的相关性,将两要素做剔除处理,构建了12个物理气象变量(解释变量)与洪水特征值分位数(响应变量)之间的变量关系。
2 研究方法
区域频率分析(RFA)主要涉及两个方面的内容:①同质区域识别与划分,采用的处理方法包括典型相关性分析(CCA)和非线性典型相关性分析(NLCCA);②区域水文分位数估计,估计模型包括多元线性回归(MLR)模型和广义加性模型(GAM)。本文通过同质区域识别方法与区域水文分位数估计方法的交叉组合,形成4种耦合模型(NLCCA-GAM,CCA-MLR,NLCCA-MLR和CCA-GAM)来估算无资料地区洪水特征值的分位数。
2.1 同质区域识别
2.1.1 典型相关分析(CCA)
典型相关分析是区域频率分析中确定水文同质区域最推荐的方法之一[35],应用较为广泛。具体原理为:若有两组随机变量X=(X1,X2,…,Xp)T和Y=(Y1,Y2,…,Yq)T,分别考虑变量X和Y的任意线性组合,得到新的规范变量u和v:
u=a1X1+a2X2+…+apXp=aX;
(1)
v=b1Y1+b2Y2+…+bqYq=bY。
(2)
式中a和b分别为典型相关系数,a=(a1,a2,…,ap)、b=(b1,b2,…,bq)。
因此,可通过建立物理气象变量和水文变量的线性组合得到新的规范变量u、v,并由u、v实现同质区的划分。
2.1.2 非线性典型相关分析(NLCCA)
非线性典型相关分析(NLCCA),通过在两组随机变量X=(X1,X2,…,Xp)T、Y=(Y1,Y2,…,Yq)T与新的规范变量u、v之间建立非线性关系,来实现同质区域识别[36]。
在实际应用中,NLCCA多与神经网络理论相结合,下面以3个前馈神经网络(NN)为例,说明NLCCA的具体执行过程(图3)。图3中,竖线以左展示了从输入X和Y映射到隐藏层h(X)、h(Y)和规范变量u、v的具体过程,其关键内容是选取适当的参数使规范变量u和v之间的相关性最大。为了充分提取原始数据信息,通过n次使用NLCCA,可得到n组u、v,并组成规范度量U、V(均为列向量)。竖线右侧显示了从U、V映射到隐藏层h(u)、h(v)和最后输出层X′、Y′的过程,其需要通过参数选取使(X,Y)和(X′,Y′)之间的均方误差最小[22]。
对于无资料地区的站点而言,站点的解释变量X对应的规范变量UO和响应变量Y对应的规范变量VO通常并不可用。因此,在区域划分中需要通过马氏距离确定100(1-α)%的置信度邻域,并考虑目标站点的规范变量VO的位置与其他站点规范变量V的位置之间的关系,使得:
(3)
其中,
式中:x2(k)为自由度为k的卡方分布;∀为由多个典型相关系数组成的n×n对角矩阵;In为n阶单位矩阵;α为显著性水平。
2.2 区域水文分位数估计
2.2.1 多元线性回归(MLR)模型
多元线性回归是一种统计技术,可对响应变量与多个解释变量之间的线性关系进行建模。本质上讲,多元回归即是普通最小二乘回归的扩展[37],其表达式为:
(4)
式中:yi为响应变量;xi1、xi2、…、xip为解释变量;p为解释变量的数量;b0为常数项;b1、b2、…、bp为回归系数;εi为随机误差;q为响应变量的数量。
2.2.2 广义加性模型(GAM)
广义加性模型是广义线性模型的扩展,可通过链接函数将响应变量链接到平滑函数[31],其表达式为:
(5)
式中:g(·)为单调链接函数;βo为截距;s(·)为光滑函数,主要是薄板样条函数;xik为解释变量。图4为GAM的结构组成示意图。

图4 GAM结构组成示意图
2.3 模型耦合与性能评估
为了探索较为适用于陕北黄土高原的区域频率分析方法,本文建立了经典线性组合CCA-MLR、半线性组合CCA-GAM/NLCCA-MLR和完全非线性组合NLCCA-GAM 4种耦合模型,开展无资料地区洪水特征值的频率计算。同时,采用相对误差(RE)和均方根误差(RMSE)两个指标进行模型性能评估。RE和RMSE的计算公式分别为:
(6)
(7)

3 结果分析
为了评价经典线性组合CCA-MLR、半线性组合CCA-GAM/NLCCA-MLR和完全非线性组合NLCCA-GAM 4种模型估算无资料地区站点洪水特征值分位数的性能,选择有实测记录的马湖峪站(马湖峪河)和高石崖站(孤山川)为目标站点,假定其为无观测站点,通过估计值与实测值的偏差来评估不同模型的效能,以确定适用于陕北黄土高原无资料区洪水特征值分位数的计算方法。
3.1 同质区域识别结果
综合考虑不同水文站点的水文特征及其与气候、地形等自然条件的关系,基于CCA划分出榆林市的水文站点同质区域(图5(a)和图5(b))。由图5(a)和图5(b)可知,以马湖峪为目标站点划分的同质区域内标识了19个站点,以高石崖为目标站点划分的同质区域内标识了20个站点,其规范变量U和V之间的相关系数分别为0.86和0.83。基于NLCCA划分的同质区域(图5(c)和图5(d))与基于CCA的有所不同,具体表现为:以马湖峪为目标站点划分的同质区域内标识了14个站点,以高石崖为目标站点划分的同质区域内标识了15个站点,其规范变量U和V之间的相关系数分别为0.97和0.93。

图5 基于CCA和NLCCA划分的同质区域
从相关系数上看,NLCCA规范变量的相关系数均高于CCA的,表明NLCCA提取出的规范变量比CCA提取出的U和V之间的相关程度更大,即对于无观测资料的站点而言,基于NLCCA划分的同质区域更具有可靠性。
从同质分区内站点的分布看,NLCCA与CCA的分区结果存在较大不同,主要表现在站点数量与空间位置的差异性上。从图5可以看出,CCA和NLCCA划分的“水文分区”并不一定要求站点的“地理位置相近”。对相同的目标站点,CCA和NLCCA划分结果的不同反映了水文特征与流域特征之间存在非线性关系,并且这种关系对水文分区有较大的影响。由图5可知,NLCCA的结果更有规律性,且目标站点的同质区域内的站点数量明显较少,换句话说,NLCCA可用更少的站点数量达到与CCA相同的划分效果。
3.2 洪水特征值分位数估算结果
应用不同耦合RFA模型对马湖峪站洪水特征值分位数进行估算,结果如图6所示。其中,图6(a)显示了马湖峪站实测数据的分位数值与各模型估算的不同重现期洪水特征值分位数,图6(b)统计了CCA-MLR、NLCCA-MLR、CCA-GAM和NLCCA-GAM模型的估计值与真实值的相对误差。

图6 马湖峪站洪水特征值分位数估算结果及其相对误差
由图6可知,马湖峪站最大|RE|值(34.74%)出现在CCA-GAM模型对Qs5估计中,最小|RE|值(3.11%)出现在NLCCA-GAM模型对Qs100估计中。CCA-MLR模型的相对误差范围为10.51%~16.46%,NLCCA-MLR模型的相对误差范围为-31.44%~-13.49%,CCA-GAM模型的相对误差范围为-16.50%~34.74%,NLCCA-GAM模型的相对误差范围为-7.82%~4.80%。从整体性能上看,4种耦合模型在马湖峪站的估算效能从高到低的排序为NLCCA-GAM、CCA-MLR、CCA-GAM、NLCCA-MLR。简单分析上述排序结果,可初步得到如下结论,即非线性同质区划分法(非同)+非线性分位数估算法(非估)优于线性同质区划分法(线同)+线性分位数估算法(线估),且两者远优于“非同+线估”或“线同+非估”。换句话说,即完全非线性组合优于经典线性组合,且两者远优于半线性组合。
图7显示了高石崖站洪水特征值分位数的估算结果及相对误差。其中,图7(a)显示了高石崖站不同重现期的实测洪水特征值分位数与不同模型的估计值,图7(b)统计了CCA-MLR、NLCCA-MLR、CCA-GAM和NLCCA-GAM模型估计值与真实值的相对误差。

图7 高石崖站洪水特征值分位数估算结果及其相对误差
由图7可知,高石崖站的估计效能较马湖峪站的有所提升,最大|RE|值(24.71%)出现在CCA-GAM模型对Qs5估计中。这一结论与马湖峪站的类似,最小|RE|值(0.82%)出现在CCA-GAM模型对Qs20估计中。
由图6(b)和图7(b)可知不同模型对不同重现期分位数估计的偏差如下:CCA-MLR模型的相对误差范围为-7.36%~16.14%,NLCCA-MLR模型的相对误差范围为-9.97%~16.14%,CCA-GAM模型的相对误差范围为-24.70%~12.42%,NLCCA-GAM模型的相对误差范围为-7.25%~-1.80%。不同模型整体性能由高到低的顺序为NLCCA-GAM、CCA-MLR、NLCCA-MLR、CCA-GAM。这一排序结果与马湖峪站前两位的排序结果一致,但NLCCA-MLR与CCA-GAM的顺序有所差异。从以上排序结果及存在的差异可以看出,马湖峪站洪水特征分位数估算中所得出的结论在高石崖站依旧适用,即完全非线性组合优于经典线性组合,且两者远优于半线性组合。
不同模型求得的马湖峪站和高石崖站洪水特征值分位数估算结果的均方根误差如图8所示。该结果也表现出了与相对误差结果一致的模型效能规律。
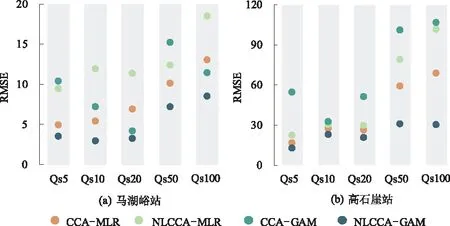
图8 马湖峪和高石崖站不同模型分位数估计的均方根误差
综上所述,可总结4种耦合模型对陕北黄土高原区马湖峪和高石崖目标站洪水特征分位数的估计效能如下:①完全非线性组合优于经典线性组合,且两者远优于半线性组合;②NLCCA-GAM模型具有最高的估计精度,相对误差最大不超过8%,且具有较强的鲁棒性,在不同重现期下均有良好表现;③CCA-MLR模型的表现不如NLCCA-GAM模型的稳定,最大相对误差不超过17%,但优于CCA-GAM和NLCCA-MLR模型的表现。
4 讨论
上述不同模型的洪水特征值分位数估算效果对比主要基于马湖峪和高石崖两个目标站展开。为了更全面准确地验证CCA-MLR、NLCCA-MLR、CCA-GAM和NLCCA-GAM模型在整个研究区的适用性,增加了横山(芦河)和丁家沟(无定河干流)2个目标站点,计算了4个耦合模型对4个目标站点(马湖峪、高石崖、横山和丁家沟)洪水特征值分位数Qs5、Qs10、Qs20、Qs50和Qs100估计的平均效能,结果如图9所示。

图9 不同模型对Qs5、Qs10、Qs20、Qs50和Qs100估计的RMSE结果
由图9可知:
1)CCA-MLR、NLCCA-MLR、CCA-GAM、NLCCA-GAM模型的RMSE变化范围分别为24.7~55.3、41.2~89.9、39.2~86.9、16.8~31.3。从整体估计精度上看,NLCCA-GAM模型明显优于其他模型,这与马湖峪和高石崖目标站所得到的结论是一致的。
2)聚焦不同重现期,可发现Qs5、Qs10、Qs20、Qs50和Qs100的最优估计(即RMSE最小值)也都是由NLCCA-GAM模型获得的。其与CCA-MLR模型相比,对Qs5、Qs10、Qs20、Qs50和Qs100的RMSE值分别降低了31%、17%、40%、29%和60%;与NLCCA-MLR模型相比,RMSE值分别降低了68%、29%、63%、65%和71%;与CCA-GAM模型相比,RMSE值分别降低了57%、36%、53%、55%和74%。由此可见,NLCCA-GAM模型在马湖峪和高石崖站所表现出的高精度和强鲁棒性,在其他目标站点也是客观存在的,NLCCA-GAM模型可作为陕北黄土高原无资料地区洪水特征值(最大一日流量)分位数的最优估计方法。
3)从不同模型的表现上看,CCA-MLR模型逊于NLCCA-GAM模型,在Qs5、Qs10、Qs20、Qs50和Qs100的估计中,在估计精度上CCA-MLR模型尽管也有相对较好的表现,但在鲁棒性或稳定性上并无太大优势,会随着重现期增加而呈现精度衰减。NLCCA-MLR和CCA-GAM模型的估计性能相对于NLCCA-GAM和CCA-MLR模型的有较大差距,并随着重现期的增加,RMSE值明显增大,稳定性较差。由此可见,马湖峪和高石崖两个目标站点估计效能分析中所得到的结论:完全非线性组合优于经典线性组合,且两者远优于半线性组合,是适用于陕北黄土高原大部分地区的。
结合前述对同质区域划分方法的分析,尽管非线性方法(NLCCA)能够获得比线性方法(CCA)更少的域内站点数量,但其同质关系主要基于非线性表达,若使用线性估计方法进行分位数估计,则很难获得较好的效果。从NLCCA-MLR模型的表现上也可以发现这一点。因此,保持同质区划分与分位数估计上的信息一致性至关重要,而对于受气候变化和人类活动非线性影响较为显著的地区而言,采用非线性的区域频率分析方法将更容易获得逼近实际洪水特征值分位数的估计值。
5 结论
本文以榆林市28个水文站点的年最大一日流量(MDF)序列为研究对象,分析了基于2种典型同质区域划分方法(CCA和NLCCA)和2种典型区域估计模型(MLR和GAM)的组合模型对陕北黄土高原无资料地区洪水特征值分位数的估算效能,确定了适用于陕北黄土高原无资料地区洪水特征值分位数的最优估算方法,得出如下结论:
1)基于CCA和NLCCA的水文同质区域划分主要基于站点相似信息,并不一定要求站点地理位置相近。对相同的目标站点,由于表征的水文特征与物理气象特征间关系不同,故CCA和NLCCA的划分结果也会存在差异性。相对而言,NLCCA的域内相关性更高,规律性更强,且可依托更少的站点数量达到与CCA相同的划分效果。
2)NLCCA-GAM模型凭借其非线性优势,具有比其他模型更高的精度和鲁棒性,在不同重现期下均可获得较为精准的估计值,且在空间表现上较为稳定,可作为陕北黄土高原无资料地区洪水特征值(最大一日流量)分位数的最优估计方法。
3)非线性的区域频率分析法(同质区域划分+分位数估计)优于线性区域频率分析法,且两者相对于线性、非线性混合耦合方法更具明显优势,也可以简单理解为:完全非线性组合优于经典线性组合,且两者远优于半线性组合。这表明,保持同质区域识别和分位数估算两者的信息一致性至关重要。
4)对于受气候变化和人类活动影响较为显著的地区,采用非线性区域频率分析方法更容易获得逼近实际洪水特征值分位数的估计值。

