改扩建路基差异沉降特性及处治研究

傅 松

(广西北投交通养护科技集团有限公司,广西 南宁 530201)

0 引言

近年来,随着国内公路路网的逐步完善,公路事业逐渐从新建阶段转向既有道路改扩建阶段。在既有道路改扩建项目中,对路基的加宽是影响后期道路运行质量和安全的关键内容,新旧路基的差异沉降会对路基拼接及路面结构产生不利影响,轻则发生路面局部沉陷,影响舒适,重则导致路面纵向开裂、路基失稳,严重影响行车安全。本文以国道G110某段改扩建项目示范段为依托,根据现场实测数据建立ANSYS模型,开展新旧路基不均匀沉降研究,为该项目示范段路基加宽工程提供理论依据。

1 工程概况及新旧路基不均匀沉降计算方法

1.1 工程概况

该项目起点位于国道G110 线K292+200处,示范段长度为500 m,采用双向四车道,设计速度为80 km/h,路基加宽采用单侧加宽方式,加宽后路基宽度为25.5 m。示范段上部土层为砂土、砂质黏土,中间土层夹有砂砾,工程地质比较稳定,整体条件较好,适宜填筑路基。

1.2 路基不均匀沉降计算方法

根据地基沉降理论,路基沉降包含三部分:瞬时沉降、固结沉降和次固结沉降。在工程实践的计算过程中,旧路基最终沉降量通常采用经验系数法:S=mSc,其中S表示最终沉降量,Sc表示固结沉降量,m为经验系数,取值为1.1～1.7。通常采用分层总和法计算固结沉降量,但是在路基拓宽工程中,新路基的修建等同于对旧路基施加新的附加应力,因此难以通过分层总和法求解。根据相关研究[1-2],可采用土力学中的Boussinesq进行求解,公式如下:

(1)

式中:S总——总沉降量;

h——地基计算深度;

Es——变形模量;

σz——附加应力。

在路基加宽工程中,σz为新旧路基共同作用产生。其中,旧路基为梯形,荷载可以分解为一个矩形与两个三角形,三部分荷载的应力叠加计算公式为:

(2)

式中:σz路中——三部分应力在旧路基中心线下z深度处的叠加应力;

p——自重应力;

A——路基三角形部分的底宽度;

B——梯形旧路基的上底高度;

z——计算深度。

项目采用单侧加宽,新路基的荷载为平行四边形,可将其等效为梯形分布,因此可套用旧路基附加应力计算方法。则新路基对地基下任意点的附加应力计算表达式为:

σz=σz旧+σz新=(n1+n2+n3)p旧+(n′1+n′2+n′3)p新

(3)

式中:n1、n2、n3、n′1、n′2、n′3——旧路基、新路基的三部分荷载附加应力系数;

p旧、p新——旧路基、新路基的附加应力代表值。

新旧路基不均匀沉降为:

ΔS=S新总+S旧总

(4)

2 有限元模型的建立

2.1 基本假定

(1)车辆荷载沿路线方向无明显差异化特性,且路基长度方向远大于宽度和高度,故可采用plane42单元,以平面应变问题进行分析;(2)假定路基与土基为弹塑性体,则路基与土基模型采用Drucker-Prager模型;(3)旧路基已完全固结;(4)新路基与旧路基的衔接处为完全连续接触,且不会出现脱离与滑移。

2.2 计算参数

根据国道G110改扩建项目示范段土样室内试验与现场勘探结果,结合有限元分析中Drucker-Prager模型特性,选取的模型计算参数如表1所示。交通荷载采用等效均布荷载,结合轻重载交通情况,将重载区域和轻载区域的均布荷载分别设置为12 kPa、10 kPa。

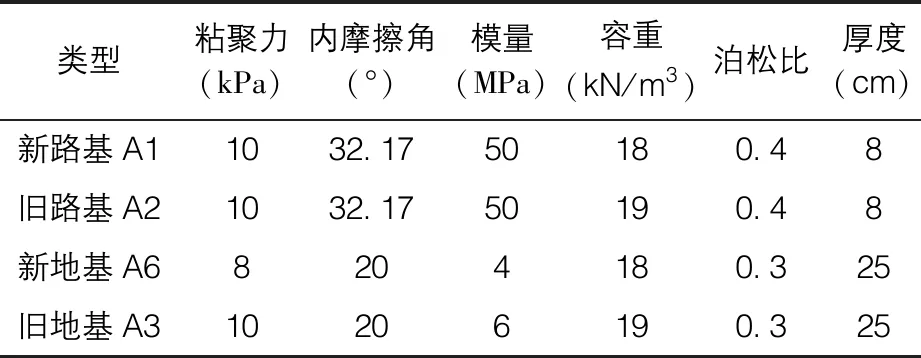
表1 模型材料参数表

2.3 模型的建立

模型根据现状及加宽后的国道G110改扩建项目示范段建立,旧路路基宽度为12.75 m,改造后路基宽度为25.5 m,采用整体式单侧加宽方式。图1所示为模型尺寸图。为保证精度,对路基与土基分别以0.5 m、1 m为单位划分自定义网格,如图2所示。

图1 模型尺寸图

图2 有限元模型网格划分示意图

3 新旧路基不均匀沉降特性分析

3.1 拓宽后竖向位移及沉降分析

路基拓宽后,新旧路基间不可避免会发生不均匀沉降。利用建立的路基-土基有限元模型,进行模拟加载和计算,得到图3、图4所示的拓宽后路基沉降值。结果表明,拓宽路基两侧沉降较小,最大沉降发生在新旧路基结合处,表现出中间大、两侧小的沉降形式。同时,与旧路基相比,新路基固结不完全,竖向有效应力小,整体沉降比旧路基大。

图3 路基表面竖向位移曲线图

3.2 不同衔接方式的沉降分析

对新旧路基衔接处采用台阶开挖和直接衔接两种工艺进行了模拟,结果如图4所示。图4的模拟结果表明,采用台阶式衔接时,最大沉降差量为3.85 cm,而直接衔接的最大沉降量达到7.03 cm,相差近一倍。其原因在于开挖台阶大大增加了新旧路基的接触面积,提高了路基的承载能力与整体性。在台阶开挖施工时,分为自上而下与自下而上两种开挖方式,其中自上而下的开挖对原路基影响较大,不利于机械化施工[3],因此本项目可采用自下而上开挖台阶的施工方式。

3.3 不同台阶尺寸的沉降分析

采用控制变量法对不同台阶尺寸下的新旧路基不均匀沉降进行分析:(1)将台阶的宽度设定为1 m,高度设定分别为0.5 m、0.8 m、1 m、1.5 m和2 m;(2)将台阶高度设定为1 m,宽度设定分别为0.5 m、0.8 m、1 m、1.5 m和2 m。模拟结果如图5～8所示。

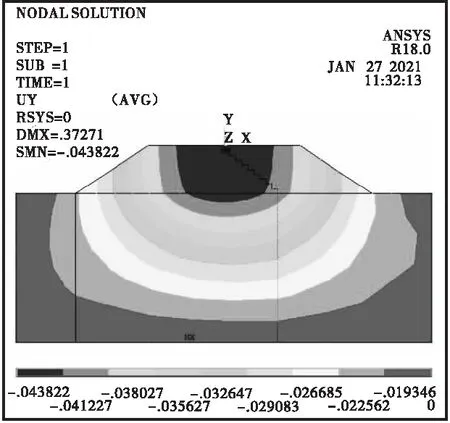
图5 不同台阶高度对路基竖向位移的影响云图

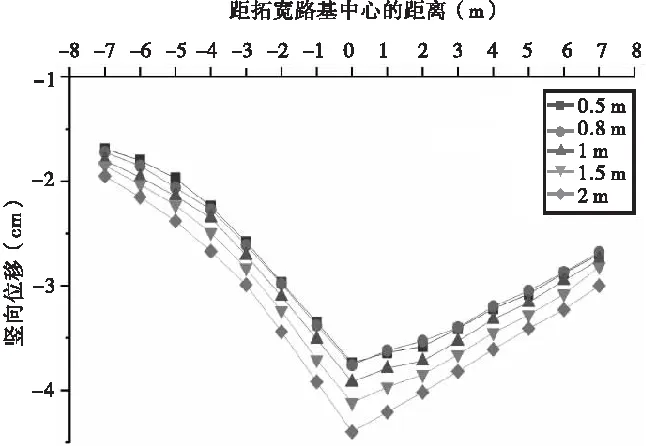
图6 不同台阶高度对路基竖向位移的影响曲线图

图7 不同台阶宽度对路基竖向沉降的影响云图

图8 不同台阶宽度对路基竖向沉降的影响曲线图

图5～6表明,当新旧路基衔接处的台阶宽度一定时,路基最大沉降值随着台阶高度的增加而增大。当台阶高0.5 m时,最大沉降为3.76 cm;当台阶高2 m时,最大沉降量为4.42 cm,相差18.2%。图7～8表明,当新旧路基衔接处的台阶高度一定时,最大沉降量及差异沉降量随着台阶宽度的增大而减小。相比台阶宽度为1 m,台阶宽度为1.5 m、2 m时的最大沉降量分别下降1.05%、2.91%,最大差异沉降量下降1.56%、3.78%。因此降低新旧路基衔接处的台阶高度、增大台阶宽度,有利于降低新旧路基不均匀沉降,但是由此可能导致开挖量过大问题,应结合项目的经济性作进一步分析。该项目结合计算分析、工程经验、工程经济,建议台阶开挖尺寸为高度0.8～1.5 m、宽度1～1.5 m,同时采用台阶内倾的方式增加新旧路基嵌固作用,内倾坡度为3%。

3.4 不同拓宽路基高度的沉降分析

本项目示范段拓宽路基高度为8 m,为分析路基沉降与拓宽路基高度不同的关系,取拓宽高度6 m、7 m、8 m、9 m、10 m分别开展模拟计算,得到如图9～10所示的不同拓宽路基高度下的沉降图。

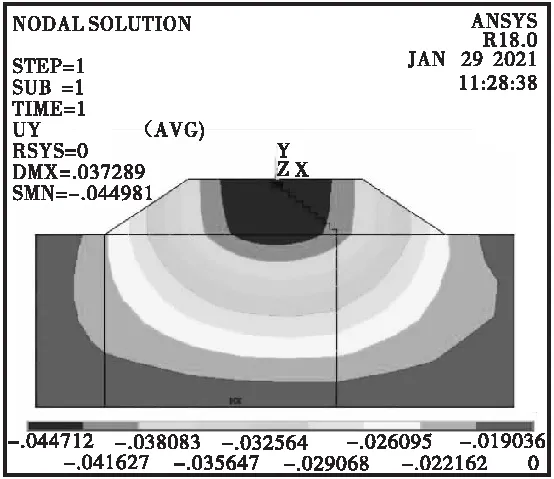
图9 不同拓宽路基高度对路基竖向沉降的影响云图

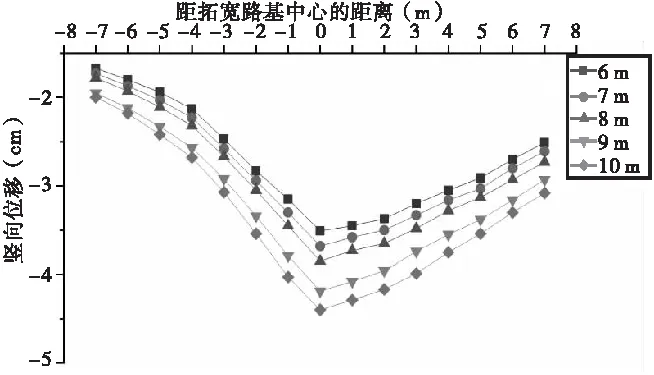
图10 不同拓宽路基高度对路基竖向沉降的影响曲线图

由图9～10可知,路基最大沉降发生的位置并不随着路基拓宽高度的变化而变化,其最大沉降仍在新旧路基结合处;随着路基拓宽高度的增加,路基沉降量及其最大差异沉降值均变大,在路基填筑高度>8 m后,路基差异沉降增长趋势变大。因此,对于道路改扩建工程中拓宽路基填筑高度>8 m的工程,需要结合其他措施如增大拓宽路基工程的压实度等方法,以有效控制和减小路基的不均匀沉降。

3.5 新路基填料对拓宽路基沉降的影响分析

(1)填料重度的影响。考虑到该项目沿线的石材状况存在差异,分别取土重度为5 kN/m3、10 kN/m3、18 kN/m3、23 kN/m3开展模型计算,具体计算结果如图11所示。计算结果表明,拓宽路基的最大沉降量和最大差异沉降量,均随着填料重度的增大而增大,且幅度较为明显。因此,在旧路拓宽项目中,采用轻质材料能够较大程度地降低新旧路基的不均匀沉降。

图11 不同填料重度对路基竖向位移的影响曲线图

图12 不同填料弹性模量对路基竖向位移的影响曲线图

(2)填料弹性模量的影响。为分析拓宽路基沉降受填料弹性模量的影响,分别取填料弹性模量值为30 MPa、40 MPa、50 MPa、60 MPa、70 MPa,开展模拟计算,具体结果如图12所示。由图12可知,路基最大沉降与最大差异沉降随着拓宽路基填料弹性模量的增加而下降。当新路基填料弹性模量为50 MPa时,最大沉降量与最大差异沉降分别为3.85 cm、2.07 cm;当填料模量增大到60 MPa时,最大沉降量与最大差异沉降分别为3.73 cm、2.00 cm,均有较为明显的下降。当填料模量进一步增大到70 MPa时,最大沉降量与最大差异沉降量分别为3.68 cm、1.97 cm,虽仍有所下降,但下降趋势明显变缓。因此在选择新建路基填料时,选择弹性模量大的材料,有利于降低不均匀沉降。但也应当注意到当填料强度和模量过高时,对拓宽路基沉降的减少效果并不显著,还可能导致工程经济效益不高[4]。

(3)填料c、φ值的影响。采用控制变量法,分析拓宽路基填料的强度指标对路基沉降的影响。当固定内摩擦角为φ=32.17°时,粘聚力c分别取值5 kPa、10 kPa、15 kPa、20 kPa、30 kPa进行模拟计算,分析粘聚力对路基沉降的影响;当固定粘聚力c=10 kPa时,内摩擦角φ分别取值10°、20°、32.17°、40°、50°进行模拟计算,分析内摩擦角对路基沉降的影响。具体结果如图13～14所示。

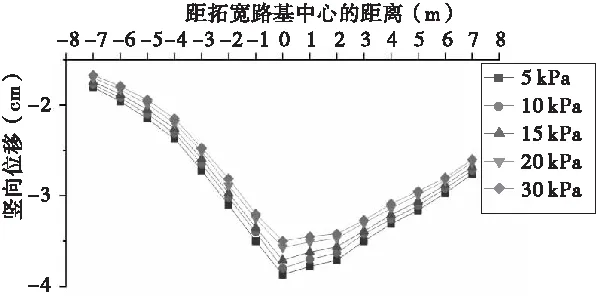
图13 不同填料粘聚力对路基竖向位移的影响曲线图

图14 不同填料内摩擦角对路基竖向位移的影响曲线图

图13～14的模拟计算结果表明,当内摩擦角一定时,拓宽路基的最大沉降量和最大差异沉降量随着粘聚力的增大而降低,相比粘聚力为5 kPa时的拓宽路基沉降量和最大差异沉降量,30 kPa时分别降低9.67%和11.71%。当填料粘聚力一定时,路基最大沉降、最大差异沉降与内摩擦力的关系与此类似。因此,为了保证新旧路基的整体稳定,降低不均匀沉降现象,路基填料应当选择具有较高内摩擦角与粘聚力的填料,结合模拟结果与本项目所在地石材条件,新路基填料的内摩擦角和粘聚力建议取值分别为5～10 kPa和30°～40°。

4 不同土工格栅处治方式对路基沉降的影响

4.1 土工格栅铺设位置对沉降的影响分析

本项目新旧路基搭接处采用土工格栅提高路基的整体性和抗变形能力。土工格栅能够通过摩擦作用、锁定作用、被动阻抗作用,降低土层间的相对位移,同时具备一定的加筋作用,提高土层强度与整体性。本次土工格栅的模型参数设定为:厚度为0.01 m,容重为18 kN/m3,模量为2 000 MPa,泊松比为0.25。为了分析路基不均匀沉降受土工格栅铺设位置的影响,土工格栅铺设于每层台阶处,台阶自下而上从台阶1至台阶9依次编号,模拟计算每次土工格栅铺设下的路基沉降情况,计算结果如图15所示。

图15 不同土工格栅铺设高度对路基沉降的影响柱状图

图16 不同土工格栅铺设铺设层数对路基沉降的影响柱状图

从图15可知,当土工格栅铺设在路基底面时,路基最大不均匀沉降为1.50 cm;当土工格栅铺设于台阶9(顶部)时,最大不均匀沉降为2.06 cm,相比铺设在路基地面时,增大37.3%。这表明随着土工格栅铺设位置的提高,土工格栅对路基沉降的作用越低。同时,随着土工格栅铺设位置越接近于顶部,路基最大不均匀沉降减小的效果越不明显。

4.2 土工格栅铺设层数对沉降的影响分析

本节分析当土工格栅从路基底层逐渐逐层向上增加时,铺设层数的增加对路基最大沉降的影响效果。模拟计算的结果如图16所示。从图16可以看出,当土工格栅仅铺设路基底部一层时,路基最大不均匀沉降量为1.50 cm;当土工格栅铺设至6层时,不均与沉降量为1.24 cm,下降17.3%;当土工格栅铺设至第9层时,不均匀沉降量为1.18 cm,下降21.3%。由此可知,路基的最大不均匀沉降量随着铺设层数的增加而降低,铺设多层土工格栅对降低路基沉降仍然具有效果,但是随着层数的不断增加,这种改善效果越不明显,且经济性较差。结合本项目,最终选择的路基铺设层数为6层。

5 结语

本文依托国道G110 线改扩建项目示范段工程,根据现场实测数据建立ANSYS有限元模型,对路基拓宽后的沉降进行模拟,分析新旧路基衔接方式、台阶高度、台阶宽度、填料重度、填料弹性模量、填料粘聚力及内摩擦角对新旧路基不均匀沉降的影响,为本项目示范段路基加宽工程提供理论依据。结果表明:(1)相比直接衔接,开挖台阶衔接方式能够降低最大沉降量近一倍;(2)路基最大沉降值随着各级台阶高度的降低、台阶宽度的增大而降低,但是考虑到开挖量过大、经济性差等问题,建议该项目台阶开挖尺寸为高度0.8～1.5 m、宽度1～1.5 m、内倾坡度3%;(3)拓宽路基的填料重度降低、内摩擦角及粘聚力增大,有利于减少不均匀沉降量,但是过度增大填料强度和模量,对拓宽路基沉降的减少效果并不十分明显,建议该项目拓宽路基填料的粘聚力和内摩擦角取值分别为5～10 kPa和30°～40°;(4)土工格栅在新旧路基搭接中的高度和层数,都对新旧路基沉降有较大影响,土工格栅铺设的位置越低,土工格栅铺设的层数越多,土工格栅减少路基沉降的作用越明显,但是当达到某一限度后,继续增加土工格栅层数对路基沉降的影响变得不显著,该项目推荐路基铺设层数为6层。