深层页岩伊利石孔隙中甲烷吸附相密度特征

杨琴，黄亮，周文，邹杰，王璐，刘逸盛，冯鑫霓

（1.成都理工大学油气藏地质及开发工程全国重点实验室，四川 成都 610059；2.成都理工大学能源学院，四川 成都 610059）

四川盆地蕴藏着丰富的页岩气资源，埋藏深度在3 500～4 500 m 的深层页岩气资源量为8.7×1012m3，占4 500 m 以浅页岩气资源总量的87%，是页岩气增储上产的重要领域［1-2］。 深化深层页岩气赋存机理认识是落实深层页岩气资源储量和扩大其生产规模的关键［3-4］。 页岩储层中黏土矿物质量分数较高［5-7］，伊利石是主要的黏土矿物类型。 页岩中伊利石纳米尺度孔隙丰富，赋存大量页岩吸附气［8-10］。

吸附气含量是指气体的绝对吸附量， 尚无法直接测量，主要通过测量的过剩吸附量进行转换。 其中，吸附相密度的确定是准确获取绝对吸附量的关键。目前，吸附相密度的实验测定仍极具挑战性， 国内外学者通过采用不同的方法获取甲烷的吸附相密度［11-19］，主要方法包括：1）液相密度法，将甲烷的常压沸点密度或Van der Waals 密度作为其吸附相密度；2） 模型拟合法，采用各种吸附模型拟合吸附曲线， 由拟合参数确定吸附相密度；3）截距法，利用过剩吸附量和气相密度在高压下的线性关系确定吸附相密度；4）积分法，对纳米孔隙中甲烷的密度剖面进行积分来确定吸附相密度。

上述方法均能在一定条件下获取较为合理的吸附相密度。 部分学者对比了不同方法的适应性［16-19］，但尚未取得一致认识。刘操等［17］认为，相比液相密度法和模型拟合法， 采用截距法确定气源岩中的甲烷吸附相密度更合理可靠。 张明杰等［18］研究发现，采用Langmuir三元模型法描述超临界甲烷在煤岩中的吸附相密度比液相密度法和截距法更为恰当。目前，大部分吸附相密度确定方法及方法的对比主要应用在较低的温度和压力条件下， 尚缺乏深层页岩气储层高温高压条件下的适应性检验。另外，在深层页岩气储层条件下，温度、压力以及孔径对纳米孔隙中甲烷吸附相密度的影响规律仍有待明确。

本文基于甲烷在深层页岩伊利石纳米孔隙中的吸附数据，分别利用Langmuir 三元模型法、截距法、积分法确定其吸附相密度和绝对吸附量， 在温度333.15～423.15 K 和压力0～90 MPa 区间内检验不同方法的适应性，分析温度、压力和孔径对甲烷吸附的影响规律。

1 甲烷吸附数据

本文吸附数据来自深层页岩伊利石纳米孔隙中甲烷吸附的分子模拟结果［20］，包括甲烷过剩吸附曲线以及纳米孔隙中的甲烷密度剖面，覆盖温度区间333.15～423.15 K 和压力区间0～90 MPa。 图1 为页岩中伊利石分子模型示意。 伊利石模型为Al1Mtv 型，分子表达式为K（Si7Al）Al4O20（OH4），具有TOT 型（二八面体型）层状结构， 一侧四面体上存在铝原子对硅原子的类质同象置换，层状结构的电负性由层间的钾离子中和。伊利石纳米孔隙呈狭缝状，孔壁由晶胞解理面切面形成，狭缝壁面物理光滑，具有表面化学非均质性。甲烷吸附的模拟细节可见文献［20］。

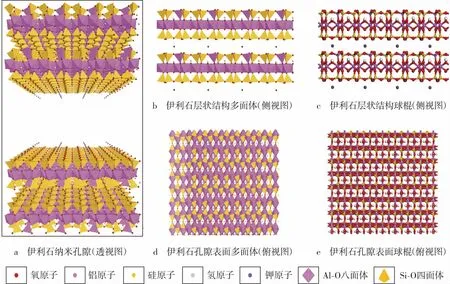
图1 页岩伊利石分子模型示意Fig.1 Schematic diagram of illite molecular model in shale

2 甲烷吸附相密度确定方法

2.1 Langmuir 三元模型法

深层页岩储层温度可达423.15 K， 压力可达90 MPa，远超甲烷的临界温度（190.55 K）和临界压力（4.6 MPa），甲烷处于超临界状态。 超临界甲烷在多孔介质中的吸附特性常用Langmuir 三元模型描述［21］。 该模型假设气体在均匀的固体表面动态吸附平衡， 气体分子间无相互作用且吸附仅形成单分子层。

Langmuir 三元模型适用于气体绝对吸附的描述。为描述气体的过剩吸附特征，需改进Langmuir 三元模型。 基于Langmuir 三元模型，结合Gibbs 吸附理论引入气相密度和吸附相密度参数， 可得到改进的Langmuir 三元模型：

式中：ne为过剩吸附量，mmol/g；VL为Langmuir 体积（极 限 吸 附 量），mmol/g；p为 气 相 压 力，MPa；pL为Langmuir 压力（吸附量达到极限吸附量50%时的压力），MPa；ρg为气相密度，g/cm3；ρa为吸附相密度，g/cm3。

相同温度下，ρg与p之间存在函数关系，ρg可由p表示的关系式代替。 基于美国国家标准与技术研究院数据库（NIST）中不同温度和压力下的甲烷气相密度数据，采用二次项函数拟合，得到甲烷气相密度与气相压力的拟合关系式（见表1。R为相关系数）。 可以看出，不同温度下的拟合系数具有较好的相关性。

表1 不同温度下甲烷气相密度与压力的拟合关系Table 1 Fitting relationships between methane gas phase density and pressure at different temperatures

在改进的Langmuir 三元模型中， 以p为自变量，以ne为因变量，以VL，pL，ρa为待拟合参数，利用模型对分子模拟的过剩吸附曲线进行非线性拟合， 可确定上述3 个拟合参数。 图2 为改进的Langmuir 三元模型拟合的过剩吸附曲线，拟合得到的参数见表2 和表3。

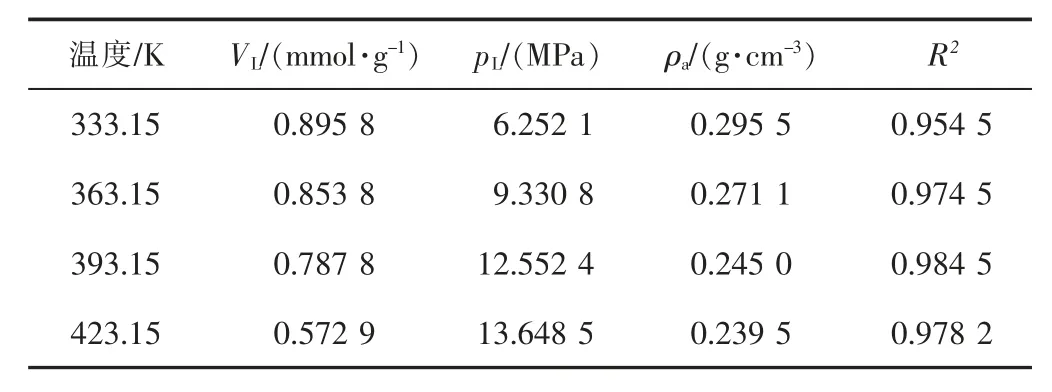
表2 不同温度下Langmuir 三元模型法拟合参数Table 2 Fitting parameters of Langmuir ternary model method at different temperatures

表3 不同孔径下Langmuir 三元模型法拟合参数Table 3 Fitting parameters of Langmuir ternary model method at different pore sizes

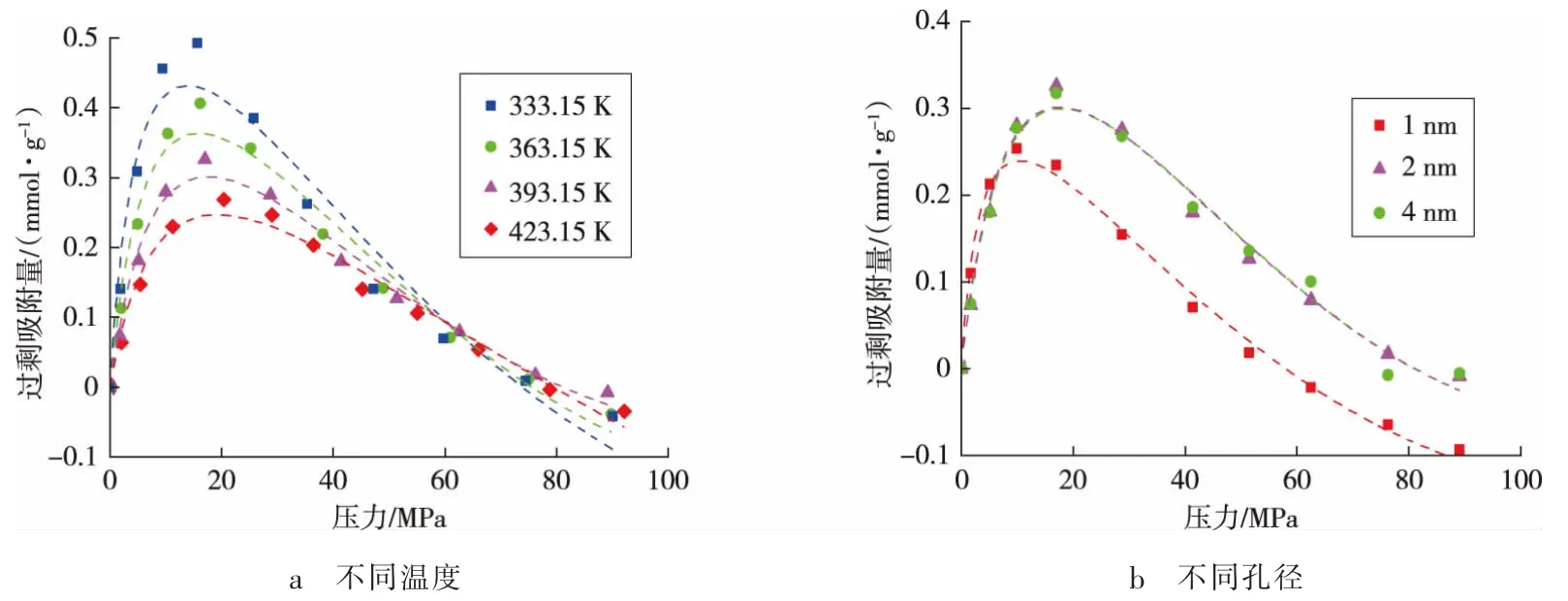
图2 Langmuir 三元模型法拟合的过剩吸附曲线Fig.2 Excess adsorption curve fitted by Langmuir ternary model

在不同温度和不同孔径下， 拟合的R2均大于0.95。 温度由333.15 K 升高至423.15 K 时，Langmuir体积从0.895 8 mmol/g 降低至0.572 9 mmol/g， 甲烷在纳米孔隙中的极限吸附能力降低。 Langmuir 压力从6.252 1 MPa 升高至13.648 5 MPa，温度升高加大了甲烷在纳米孔隙中的吸附难度。随着温度升高，吸附相密度呈减小趋势，与煤样上的研究结果一致［18］。

2 nm 和4 nm 孔隙中的拟合参数较为接近，其Langmuir 体积、Langmuir 压力以及吸附相密度均大于1 nm 孔隙中的拟合结果。 由于吸附空间限制，1 nm 孔隙中的甲烷极限吸附量更低， 但受到孔壁耦合吸引作用影响，甲烷吸附难度降低。

2.2 过剩吸附曲线截距法

甲烷在页岩纳米孔隙中的绝对吸附量可由其吸附相密度和吸附相体积确定：

式中：na为绝对吸附量，mmol/g；C为单位换算常数，本文取值3.877 91×1020mmol/g2；Va为单胞盒子内的吸附相体积，cm3。

根据Gibbs 过剩吸附定义， 由绝对吸附量扣除吸附相体积中的气相甲烷量可得到过剩吸附量［15］：

式（3）中，当甲烷在高压条件下达到最大吸附状态，吸附相密度和吸附相体积均为定值。 此时，甲烷过剩吸附量与气相密度呈线性函数关系。

截距法基于过剩吸附量与气相密度在高压下的线性关系确定吸附相密度，主要步骤为：1）以过剩吸附量为纵坐标，以甲烷气相密度为横坐标作关系图；2）利用式（3）对高压下的直线段进行线性拟合；3）由拟合的直线斜率确定吸附相体积， 由拟合的直线截距确定吸附相密度。

图3 为截距法拟合的过剩吸附曲线直线下降段，不同温度和不同孔径下的拟合结果见表4 和表5。2 nm 和4 nm 孔隙中的吸附相体积和吸附相密度较为接近，均大于1 nm 孔隙中的拟合结果。 由于吸附空间限制，1 nm 孔隙中孔壁附近的吸附相体积相互耦合重叠，未充分扩展。

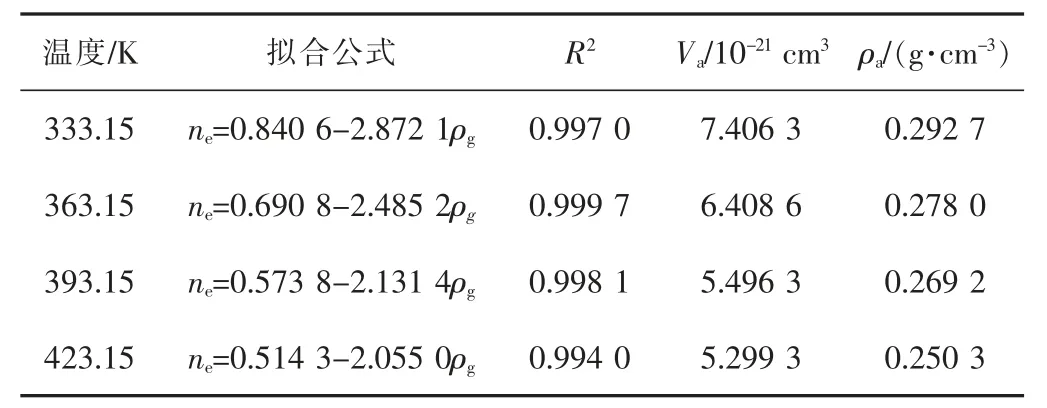
表4 不同温度下截距法拟合结果Table 4 Fitting results of intercept method at different temperatures

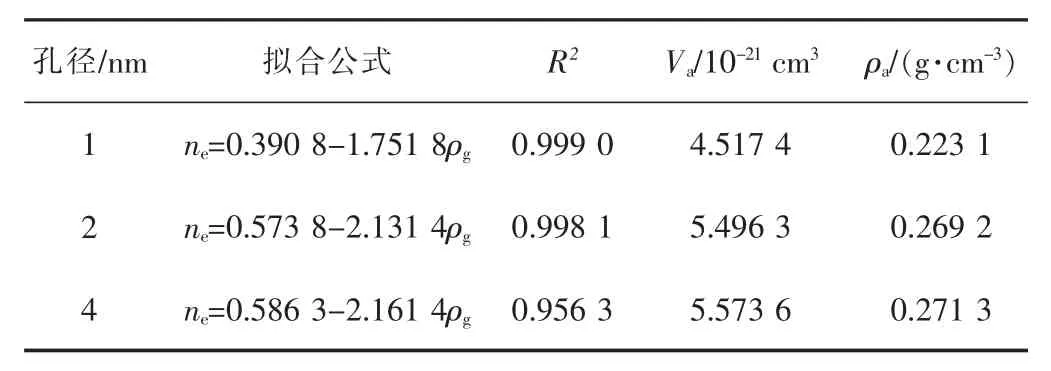
表5 不同孔径下截距法拟合结果Table 5 Fitting results of intercept method at different pore sizes

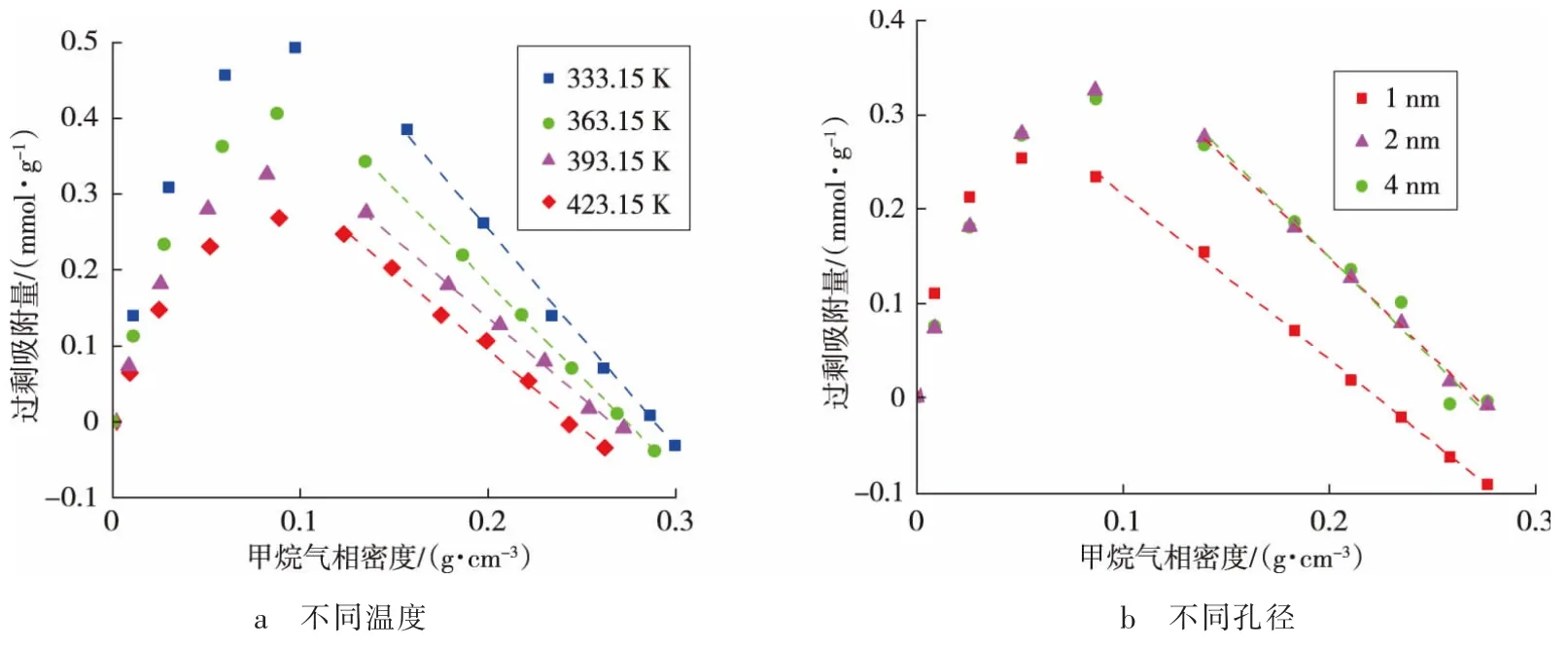
图3 截距法拟合的过剩吸附曲线Fig.3 Excess adsorption curve fitted by intercept method

拟合结果显示出较好的相关性（R2>0.95），纳米孔隙中的甲烷过剩吸附量在达到最大值后， 符合线性下降趋势。 当温度从333.15 K 升高至423.15 K 时，吸附相体积从7.406 3×10-21cm3降至5.299 3×10-21cm3，吸附相密度从0.292 7 g/cm3降至0.250 3 g/cm3。温度升高使得纳米孔隙表面的吸附相体积收缩， 吸附相密度变小。相比吸附相密度，甲烷吸附相体积对温度的敏感性更大。 温度由333.15 K 升高至423.15 K 时，吸附相体积下降幅度为28.45%，吸附相密度下降幅度为14.49%。

2.3 甲烷密度剖面积分法

不同于等温吸附实验， 分子模拟可直观观察吸附平衡后甲烷在纳米孔隙中的微观分布。 基于甲烷密度剖面，可划分吸附相区域并由积分法确定吸附相密度。图4 为甲烷在2 nm 孔隙中吸附平衡后的密度剖面。受到孔壁原子的吸引作用， 甲烷分子在2 个孔壁附近各形成1 个吸附层。 吸附层内的甲烷密度显著高于美国国家标准与技术研究院数据库中相同温度、 压力下的甲烷气相密度。 本文中将点A与点B之间的区域以及点A'与点B'之间的区域定义为吸附相。 其中，点A和点A'为有效孔隙体积的边界，点B和点B'为孔壁附近第1 个波峰与第2 个波峰之间的波谷位置。 通过对吸附相内的甲烷密度剖面进行积分并取平均值， 可得到甲烷吸附相密度：

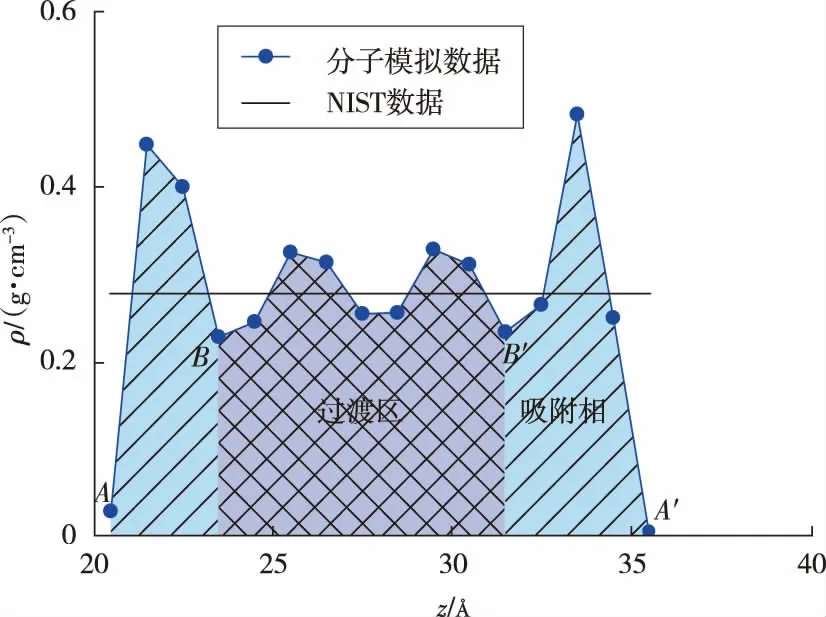
图4 甲烷密度剖面积分法示意Fig.4 Schematic diagram of methane density profile integral method

式中：ρ（z）为孔壁法向上位置z处的甲烷密度，g/cm3；zAB为点A与点B之间的横坐标距离，Å；zB'A'为点B'与点A'之间的横坐标距离，Å。

由于伊利石孔壁上吸附位点非均匀分布， 两侧孔壁附近的吸附相不完全对称， 这与前人的研究结果一致［22-24］。图4 中点B与点B'之间的区域划分为过渡区，过渡区的甲烷密度在气相密度附近小幅度波动， 其平均密度接近于气相密度。

3 甲烷吸附相密度特征

3.1 温度和压力的影响规律

图5 为不同温度、压力下2 nm 孔隙中的甲烷吸附相密度。 由图5a 可知：3 种方法计算得到的甲烷吸附相密度呈类似变化趋势，均随温度升高而降低。前人基于煤样的甲烷等温吸附实验［18］，结合Langmuir 三元模型拟合法和截距法得到了相同的温度影响规律。 随着温度增加， 纳米孔隙壁面对附近甲烷分子的吸引作用减弱，导致甲烷吸附相密度降低。

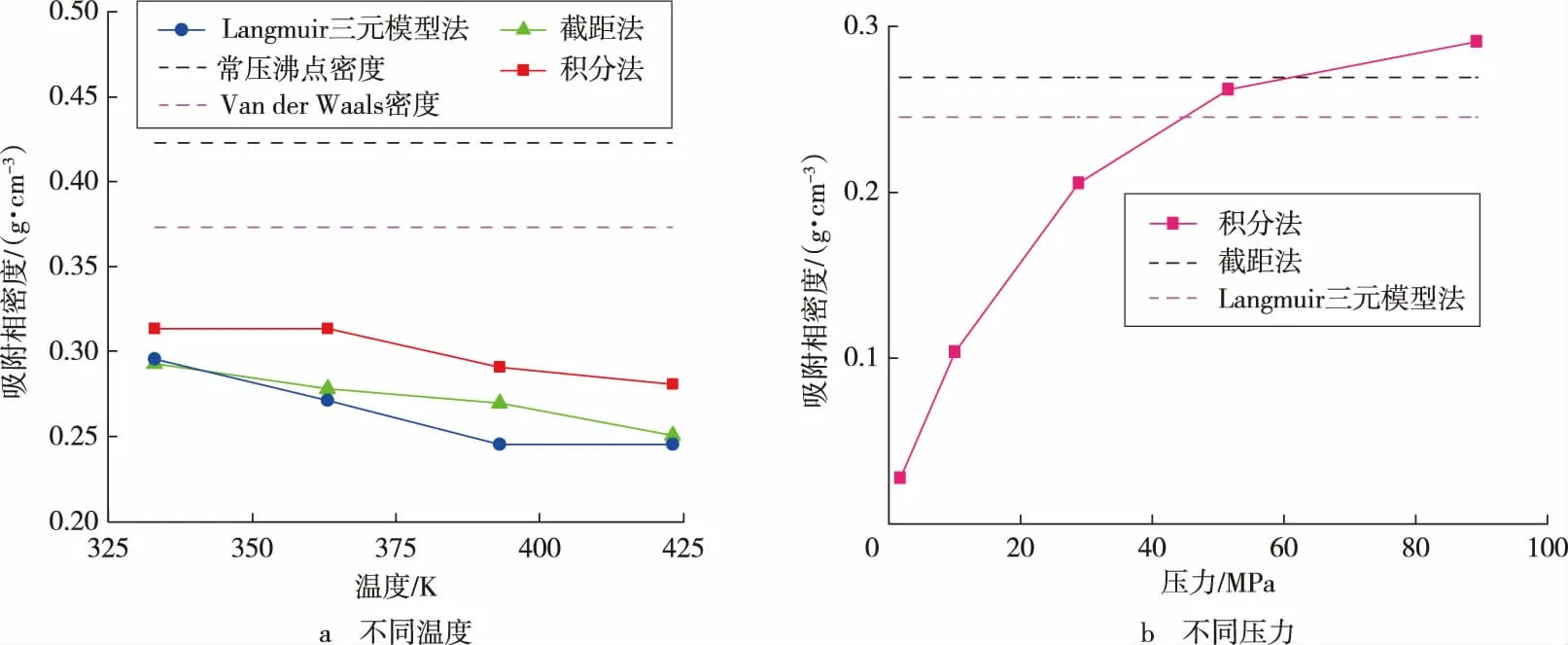
图5 不同温度和压力下的甲烷吸附相密度Fig.5 Adsorption phase density of methane at different temperatures and pressures

页岩纳米孔隙中超临界甲烷的吸附相密度应具有合理的取值范围， 其数值应当大于甲烷临界密度（0.163 g/cm3）， 小于Van der Waals 密度与甲烷常压沸点密度（0.424 g/cm3）［15，18］。本文中的3 种方法计算得到的甲烷吸附相密度均低于Van der Waals 密度与常压沸点密度， 处于合理密度窗口范围。 由图5a 可知，Langmuir 三元模型法和截距法的计算结果均为吸附达到最大后的甲烷吸附相密度， 两者的计算结果较为接近，但均低于约90 MPa 时积分法确定的吸附相密度。

Langmuir 三元模型法和截距法不能直接研究压力对甲烷吸附相的影响，1 条等温吸附曲线仅能得到吸附量达到最大后的吸附相密度。相比而言，积分法可直接获取不同压力下的吸附相密度。 由图5b 可知：甲烷吸附相密度随压力升高而增大，高压下增幅变小，但在研究的最大压力下尚未达到最大值。 前人采用固定吸附相体积假设计算了不同压力下的吸附相密度［18］，发现煤样上的甲烷吸附相密度在25 MPa 下基本达到最大值。相比煤样，伊利石纳米孔隙中的甲烷吸附相密度需在更高的压力下趋于最大值。积分法计算结果表明，压力对甲烷吸附相密度具有重要影响， 高压下吸附相密度的假设有待进一步论证。

3.2 孔径的影响规律

图6 为温度393.15 K 时不同孔径下的甲烷吸附相密度。其中，Langmuir 三元模型法和截距法计算结果为吸附达到最大值后的吸附相密度， 积分法计算结果为约90 MPa 时的吸附相密度。 不同孔径下，积分法计算结果均大于Langmuir 三元模型法和截距法计算结果。 3 种方法的计算结果均表明，2 nm 和4 nm 孔隙中的吸附相密度接近， 且大于1 nm 孔隙中的吸附相密度。 在1 nm 孔隙中，甲烷分子与有效孔隙空间的尺寸相当接近［24］，孔壁与甲烷分子之间的排斥作用凸显，使得孔隙中甲烷吸附相密度降低。 甲烷在10 nm 和20 nm 孔隙中的吸附相密度较为接近， 均低于2 nm 和4 nm 孔隙中的计算结果。 在2 nm 和4 nm 孔隙中，两侧孔壁对孔隙内的甲烷分子具有强耦合的吸引作用。 随孔径增加，孔壁耦合作用逐渐减弱至消失，导致甲烷吸附相密度降低。

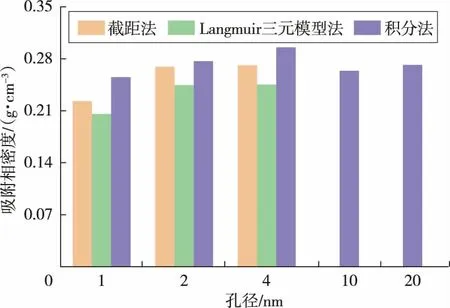
图6 不同孔径下的甲烷吸附相密度对比Fig.6 Comparison of methane adsorption phase density at different pore sizes

4 甲烷绝对吸附量校正方法

绝对吸附量是气体在多孔介质中的真实吸附量，其计算数据涉及气体的吸附相密度或者吸附相体积。本文结合Langmuir 三元模型法、截距法以及积分法获取的重要参数校正甲烷的绝对吸附量。

Langmuir 三元模型法基于Langmuir 体积和Langmuir 压力，预测甲烷在不同压力下的绝对吸附量：

本文首先采用Langmuir 三元模型法拟合分子模拟的过剩吸附曲线； 其次， 获取不同温度和孔径下的Langmuir 体积和Langmuir 压力参数；最后，利用式（5）预测对应温度和孔径下的甲烷绝对吸附量。

截距法通过拟合过剩吸附量与气相密度在高压下的线性关系，确定甲烷的吸附相密度和吸附相体积。本文基于截距法确定的吸附相体积，结合式（6）校正甲烷的绝对吸附量：

积分法通过对吸附相内的甲烷密度剖面进行积分，确定纳米孔隙中的甲烷吸附相密度。在规则的狭缝状纳米孔隙中， 甲烷吸附相体积可由孔壁面积和吸附层厚度的乘积确定。 本文设定狭缝孔单壁表面积为3.006 7×10-13cm2，吸附相厚度随孔径变化，参考先前的分子模拟数据［20］确定。因此，基于积分法的甲烷绝对吸附量校正公式为

式中：S为狭缝孔面积，cm2；d为吸附相厚度，cm。

5 甲烷绝对吸附量特征

5.1 温度和压力的影响规律

图7 为不同温度和压力下2 nm 孔隙中的甲烷绝对吸附量校正结果。对比3 种校正方法，温度对绝对吸附量的影响规律相同， 高温减弱纳米孔隙壁面对甲烷分子的吸引作用， 降低甲烷绝对吸附量。 温度由333.15 K 升高至423.15 K 时，Langmuir 三元模型法的绝对吸附量降低40.4%（约90 MPa 条件下），截距法的饱和绝对吸附量降低40.4%， 积分法校正结果受升温影响较小，绝对吸附量降低10.7%（约90 MPa 条件下）。

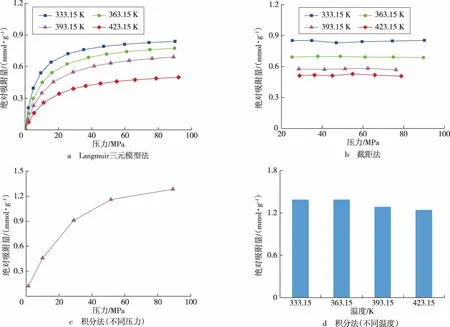
图7 不同温度和压力下的甲烷绝对吸附量校正结果Fig.7 Correction results of absolute adsorption capacity of methane at different temperatures and pressures

在3 种校正方法中， 甲烷绝对吸附量随压力增加呈现2 种变化规律：1）单调上升型，见图7a 的Langmuir三元模型法校正结果和图7c 的积分法校正结果；2）直线平台型，见图7b 的截距法校正结果。其中，截距法假设甲烷在高压阶段的吸附相密度和吸附相体积均为定值，吸附达到了最大值，故校正的甲烷绝对吸附量在30 MPa 时已达到最大。 在333.15 K 条件下的2 nm 孔隙中， 截距法确定的吸附相体积为7.406 3×10-21cm3，结合固定的伊利石狭缝孔单壁表面积为3.006 7×10-13cm2，折算得到甲烷吸附相宽度为2.46×10-8cm，远低于甲烷分子的动力学直径3.73×10-8cm，不具备合理的物理意义。

随着压力的增加，Langmuir 三元模型法和积分法校正的绝对吸附量逐级增大，高压下增幅变小。在深层页岩气储层条件下，甲烷的绝对吸附量未达到最大值。相比Langmuir 三元模型法校正结果，积分法校正的绝对吸附量更大， 约90 MPa 时其校正结果为Langmuir三元模型法校正结果的1.87 倍。Langmuir 三元模型具有3 个待拟合参数， 且拟合过程中需要人为设定待拟合参数的初始值和边界值， 具有较大的不确定性和人为误差。

5.2 孔径的影响规律

图8 为393.15 K 时不同孔径下的甲烷绝对吸附量校正结果。 由图8a 可知：低于10 MPa 时，不同孔径下甲烷绝对吸附量差异较小；高于10 MPa 时，2 nm 和4 nm 孔隙中绝对吸附量接近， 大于1 nm 孔隙中的校正结果。 由图8b 可知：高于30 MPa 以后，不同孔径下的绝对吸附量均达到最大值。 对比Langmuir 三元模型法和截距法，孔径对甲烷绝对吸附量的影响规律相同。

图8 不同孔径下的甲烷绝对吸附量校正结果Fig.8 Correction results of absolute adsorption capacity of methane at different pore sizes

由图8c 可以看出：2 nm 和4 nm 孔隙中的绝对吸附量最大， 其次为10 nm 和20 nm 孔隙中的绝对吸附量，1 nm 孔隙中的绝对吸附量最小。 孔径的影响规律反映甲烷在不同孔径纳米孔隙中的吸附机理差异。 2 nm 和4 nm 孔隙中，甲烷吸附相空间充分扩展，且孔壁对甲烷分子具有较强的耦合吸附作用， 使得绝对吸附量增加；1 nm 孔隙中孔壁对邻近甲烷分子的排斥作用增强，10 nm 和20 nm 孔隙中壁面的耦合吸附作用消失，导致绝对吸附量降低。在相同孔径、温度、压力条件下，3 种方法确定的甲烷绝对吸附量存在差异。 这是由于3 种方法基于不同的数据类型以获取绝对吸附量校正的重要参数，其中Langmuir 三元模型法基于甲烷过剩吸附曲线， 截距法基于甲烷过剩吸附量与气相密度的关系曲线，积分法基于纳米孔隙中的甲烷密度剖面。另外，3 种方法不同的假设条件和校正思路也是导致计算结果差异的重要原因。

相比Langmuir 三元模型法和截距法，基于分子模拟数据的积分法对深层页岩纳米孔隙中甲烷吸附相密度的确定具有较好的适应性，其主要优点包括：1）能够确定不同压力下吸附未达最大值的甲烷吸附相密度；2）能够合理反映压力、温度和孔径对吸附相密度和绝对吸附量的影响规律；3）能够直观还原甲烷在纳米孔隙中的微观状态和分布机理；4）能够避免数据拟合过程中的人为误差。 但积分法主要适用于形状规则且表面光滑的纳米孔隙，页岩复杂不规则、表面粗糙，复合孔隙介质中的甲烷吸附相密度确定方法还有待深入探究。

6 结论

1）温度升高减弱纳米孔隙表面对甲烷分子的吸引作用，降低甲烷吸附相密度和绝对吸附量，积分法校正的绝对吸附量在高压下受温度影响较小。

2）随压力升高，甲烷吸附相密度增加，高压下增幅变小。深层页岩气储层压力下，甲烷绝对吸附曲线上升趋势明显，甲烷绝对吸附量的增量仍较大。甲烷吸附相密度和绝对吸附量在高压下仍受压力影响。

3）纳米孔隙的临界孔径为2 nm 和4 nm，其孔壁耦合的强吸引作用以及吸附相的扩展导致甲烷吸附相密度和绝对吸附量达到最大。

4）Langmuir 三元模型法和截距法不能反映压力影响规律，Langmuir 三元模型法拟合结果受人为因素影响较大，截距法结果不具备合理物理意义，积分法对深层页岩纳米孔隙中甲烷吸附相密度的确定具有较好的适应性。