一种齿轮差动式恒速传动装置的方案设计

刘小刚，冯冠华，白文博，杨新坤

（1.秦川机床工具集团股份公司，陕西 宝鸡 721009；2.陕西法士特齿轮有限责任公司，西安 710119）

0 引言

为了在某一变转速的主动力输入条件下，能够从主动力机构中获取恒定的输出转速，进而为发电机等需要定速运转的部件提供动力的传动机构称为恒速传动装置。恒速传动装置多用于航空[1]75（例如航空发动机的CSD装置）、船舶[2]23、风力发电[3]等行业。

齿轮传动具有体积小、质量轻、传动比范围大、效率高、运转平稳、噪声低等优点，广泛应用于机械传动中。而差动传动作为一种特殊的齿轮传动，近年来越来越多地应用到工程实际当中，尤其是行星齿轮差动传动，应用非常广泛。本文针对某试验台的试验需求，提出一种利用行星齿轮差动传动原理的恒速传动装置，并对其传动过程当中的转速、转矩、功率关系等进行推导，为同类型的恒速传动装置的正向设计分析提供参考方法。

1 传动原理

本文为某试验台所设计的恒速传动装置的输入有两个，分别为主输入和调速输入，传动原理如图1所示。其中主输入是动力的主要输入部分，提供主要的动力来源，但因原动机的特性，主输入具有转速不稳定的缺陷。调速输入为辅助输入，其主要目的是根据主输入的转速变化调节自身转速并且输入给传动装置，进而使传动装置的最终输出转速为某一恒定值。

图1 某试验台用齿轮差动式恒速传动装置原理图

在本文恒速传动装置中，主输入经由一级平行轴齿轮Z5和Z6减速，动力传递至行星级的行星架Zb；调速输入经由两级平行轴齿轮Z1、Z2和Z3、Z4减速至行星级的太阳轮Za，行星级分别由行星架Zb和太阳轮Za输入，由内齿圈Zc输出。根据要求，齿圈输出为恒速6000 r/min，供发电机使用。

由图1可知，本文恒速传动装置的主要作用是当主输入转速n2发生变化时，可通过调速输入n1对输出转速进行调节，使得输出转速n3恒定为6000 r/min。而主输入转速n2和调速输入转速n1之间的转速调整关系还需进一步分析明确，以便于将调整关系式输入至电控系统，实现对调速输入转速n1的调节。另外，为了对恒速传动装置的机械结构进行详细的设计计算，还需研究装置中各个部件传递的转矩及功率关系，进而才能对各构件的强度、刚度进行校核计算。

2 转速关系

由前面的原理图分析可知，本文恒速传动装置有2条功率传递路径，第一条路径为：从主输入转速n2，经由Z5和Z6减速，传递至行星架Zb，再由行星架Zb传递至齿圈输出Zc，如图2所示。第二条路径为：从调速输入转速n1，经由Z1和Z2、Z3和Z4减速，传递至行星级太阳轮Za，再由太阳轮Za传递至内齿圈Zc输出，如图3所示。在单独分析每条功率传递路径上的转速、功率和转矩关系时，另一路径的输入应视为固定接地连接。

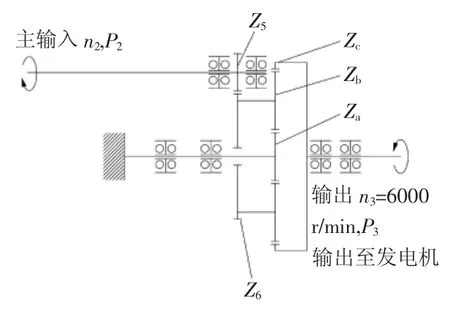
图2 第一条功率传递路径

图3 第二条功率传递路径

根据文献[4]112，行星差动机构的总传动比等于各功率流单独流经路线上行星机构的传动比之和，又由文献[5]95-96可知，图2中当太阳轮Za固定、行星架Zb输入、内齿圈Zc输出时，行星级传动比计算公式为

图3中，当行星架Zb固定、太阳轮Za输入、内齿圈Zc输出时，行星级传动比计算公式为

因此该装置的转速关系式为

3 转矩关系

在该装置的结构设计过程中，后期还要对各个构件进行强度、刚度和疲劳分析，这就需要明确每一个构件上承受的转矩。

对于单独的行星齿轮传动而言，各个构件上的转矩应达到平衡才能正常工作。又根据文献[5]95-96，行星架的假想齿数为Za+Zc，而构件上的转矩与齿数成正比，所以太阳轮Za与齿圈Zc的转矩比值计算公式为

太阳轮Za与行星架Zb的转矩比值计算公式为

行星架Zb与齿圈Zc的转矩比值计算公式为

考虑平行级速比后，将式（4）～式（6）整理合并可得主输入转矩T2、调速输入转矩T1和输出转矩T3之间的关系式：

其中：

4 功率关系

输出功率和转速恒定，因此输出的转矩T3（内齿圈的Tc等于输出的转矩T3）亦恒定，根据式（7）可得：

合并式（10）、式（11）可得

式（12）即为该恒速传动装置两输入之间的功率关系。对于某一确定的方案，当各齿轮齿数及输入转速确定后，即可确定P1和P2的数量关系，能够为设计及控制系统提供数据参考。另外，本文作为原理分析，以上公式推导均未考虑传动效率。

5 方案实施分析

根据以上传动原理，并结合行星轮系中齿数与行星轮数应满足的传动比条件、同心条件、装配条件和邻接条件[6]463-464，确定各齿轮参数，如表1所示。

表1 各齿轮齿数

将表1中的齿数分别代入式（3）、式（7）、式（12）可得：

以上关系式表明了主输入和调速输入之间的转速、转矩及功率关系。为了进一步探究这2个输入之间的关系，将以上关系式引入不同工况下的主输入转速，将计算结果汇总，如表2所示。从表2可以看出，两输入功率P1和P2的代数和为恒定值60.24 kW，符合恒功率输出的要求。将式（13）和式（15）转化为曲线图，如图4、图5所示。

表2 转速功率数据关系表

图4 主输入转速与调速输入转速关系图

图5 主输入功率和调速输入功率关系图

从图4和表2 可以看出，当主输入转速大于10 593.94 r/min，调速输入功率小于0，主输入功率P2将被分解为调速功率P1和输出功率P3；当主输入转速小于10 593.94 r/min，调速输入功率P1大于0，输出功率P3是由主输入功率P2和调速功率P1合并而成。因此，若主输入转速有在10 593.94 r/min左右工作的工况，调速输入系统应被设计成既有功率输入又有功率输出的系统。

若调速装置的电控系统不允许出现分解运动，则主输入的转速工作范围为0～10 593.94 r/min。根据图5，主输入的功率工作范围为0～60.24 kW，对应的调速输入转速为89 891.67～0 r/min，调速输入功率为60.24～0 kW。

6 建模仿真

以上针对该恒速传动装置的分析和研究是从其传动原理入手进行的正向推导求解，除了通过制造产品对其合理性进行试验验证外，还可借助仿真软件进行建模仿真分析。鉴于Romax在齿轮传动领域应用广泛，本文在Romax中建立所设计的恒速传动装置仿真模型，对其转速、转矩及功率关系进行仿真验证。根据图1创建的Romax仿真模型如图6所示。

图6 Romax仿真模型

在Romax模型中依次输入表2中的主输入转速n2，调速输入转速n1和主输入功率P2，根据式（13）～式（15），其他参数可通过模型计算确定，对比计算结果与算式计算结果是否一致。为了验证推导的关系式的正确性，主输入载荷的输入按2种方式输入：恒功率输入和恒转矩输入。图7为恒转矩输入的计算结果，图8为恒功率输入的计算结果。从计算结果可以看出：1）在模型中按照式（13）设定的主输入转速n2和调速输入转速n1计算，得出的输出转速恒定为6000 r/min，符合式（13），满足要求；2）主输入转矩T2与调速输入转矩T1及输出转矩T3的数量关系完全符合式（14）；3）主输入转速n2、调速输入转速n1、主输入功率P2和调速输入功率P1完符合式（15）；4）在恒功率输入的验证情况下，所有参数亦符合式（13）～式（15）。因此，Romax仿真模型的计算结果与采用本文的正向推导方法建立的恒速传动装置的功率、转矩及转速的计算结果完全一致。

图7 恒转矩输入的计算结果

图8 恒功率输入的计算结果

另外，从计算结果还可以看出：当主输入转速小于10 594 r/min时，主输入功率P2与调速输入功率P1的代数和等于输出功率P3，属于合成运动，其功率流向如图9所示；当主输入转速等于10 594 r/min时，调速输入转速n1和调速输入功率P1均为0，其功率流向如图10所示；当主输入转速大于10 594 r/min时，主输入功率P2与调速输入功率P1的代数差等于输出功率P3，属于分解运动，其功率流向如图11所示。

图9 合成运动功率流

图10 调速为0的运动功率流

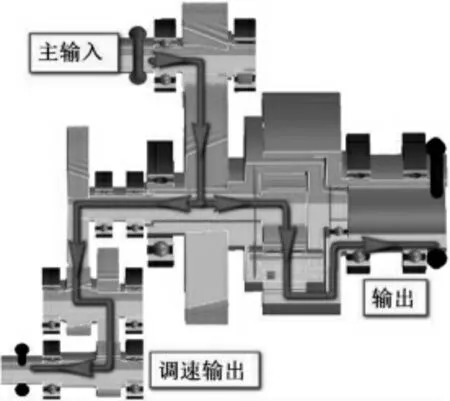
图11 调速为0的运动功率流

7 结语

对于恒速传动装置这种特殊的齿轮传动类型，本文在分析其传动内在本质的基础上提出一种差动齿轮传动装置。利用差动齿轮传动的相关理论进行正向求解分析，得出其动力传递的规律。采用齿轮传动仿真软件对这种方法进行验证后发现，仿真结果与正向求解结果完全一致，可为广泛应用于航空、船舶、风力发电等行业的恒速齿轮传动装置的设计开发提供借鉴。