基于机理与数据驱动的热连轧板凸度组合预测

陈 楠,李 旭,栾 峰,丁敬国,李 影,张殿华

(1.轧制技术及连轧自动化国家重点实验室(东北大学),沈阳 110819;2.东北大学 计算机科学与工程学院,沈阳 110819)

热轧带钢在整个工业体系中占据重要地位,其中板形是衡量其产品质量是否合格的一项重要指标,而有效控制板凸度可减少楔形等缺陷的出现,保证良好的平直度[1],确保带钢轧出板形良好,改善产品质量。传统控制手段一般将检测装置、数学模型、轧制制度、参数设定等因素有效结合,文献[2]考虑影响轧辊磨损的几个主要因素得出简单使用的磨损预报模型,具有较高预报精度。文献[3]提出一种新的板凸度分配设定方法,开发了计算板凸度调整和CVC工作辊横移设定的软件,其结果优于现场设定结果。文献[4]建立了热轧带钢工作辊平均磨损的简易计算公式,最大误差在10%左右。文献[5-6]根据工作辊磨损规律以及磨损轮廓曲线建立工作辊磨损预报模型,以遗传算法优化参数,使得模型精度可靠实用,此外针对不均匀“猫耳”磨损轮廓现象,提出了一种基于指数阻尼正弦函数的VSS换挡策略,降低局部“猫耳”轮廓值,提高凸度高精度率。文献[7]提出了一种引入磨损速率修正系数的轧辊磨损预报模型的改进方法,并对模型参数进行优化,提高了轧辊磨损预报精度。文献[8]提出一种适用于1 250 mm热连轧工作辊磨损的控制策略,减小工作辊磨损量,且磨损更均匀,延长工作辊寿命。但实际轧制过程具有强耦合、多变量、非线性、时变性等特点,其内在机理十分复杂,存在不确定的未知因素,很难获得精准的数学模型,也难以通过有限元法进行精准表述,板形控制技术的发展出现了瓶颈。

由于神经网络自身的非线性以及自适应信息处理能力,诸多研究人员已成功应用机器学习来解决轧制领域问题,例如:文献[9]将人工神经网络与遗传算法相结合,选择最佳工艺参数,获得良好平直度。文献[10]使用最小二乘支持向量机和偏差更新的热轧机软传感器设计,使用带有偏差更新项的软传感器准确地对整个过程进行建模。文献[11]以有限元计算值为训练样本,采用改进的快速BP训练算法,提高训练速度,加快网络收敛速度。文献[12]将GA-PIDNN控制器用于有效控制板凸度的缺陷,快速跟踪板凸度的目标值,提高控制精度,实现良好控制。文献[13]提出了一种基于KNN回归算法的轧制力预测模型,该法在训练时间和训练精度方面均优于线性回归算法。文献[14]提出一种采用DE算法优化SVR的凸度预测模型,相较GA-SVR模型在提高精度的同时明显减少训练时间。文献[15]建立了基于随机森林集成方法的宽厚板板凸度预测模型,利用PCA与聚类方法处理数据并提出基于关联规则的关键工艺参数调控策略,经仿真分析,该方法可较好地控制板凸度。

本文立足于热连轧现场轧制过程中多积累的大量工业数据,基于现场数据的深度挖掘,将现有的板凸度机理预测模型与数据驱动模型相结合进而构建热连轧出口板凸度组合预测模型,对热连轧出口板凸度预测模型进行性能指标分析,评估该方法的应用性与可行性,从而达到提高板凸度预测精度的目的。

1 热连轧板凸度机理预测模型

热轧板带钢凸度取决于有载辊缝形状,在轧制过程中,其受到多方面因素的影响,主要包括使辊系弯曲变形的轧制力和弯辊力、改变轧辊辊型的轧辊热变形和轧辊磨损变形等。因此可由以下方程[16]进行描述:

(1)

式中:C为热轧板带钢凸度;P、F分别为使辊系发生弯曲变形的轧制力和弯辊力;KP、KF分别为轧机轧制力横向刚度、弯辊力横向刚度;ωC为可控辊型辊凸度,根据具体采用的技术(如PC、CVC等)来确定;ωH为由轧辊热膨胀导致的轧辊热凸度;ωW为由轧辊磨损导致的轧辊磨损凸度;ω0为轧辊初始辊凸度;Δ为入口带钢凸度;E0、EC、EΣ为相应系数。

结合实际生产现场对板凸度模型进行简化,简化后机理预测模型(mechanism prediction model,MPM)表达式如下:

C=k1P+k2F+k3(ωH+ωW)+k4

(2)

其中轧辊热凸度及磨损凸度通过计算求得,轧制力、弯辊力则通过实际轧制现场提取。相关系数从实际生产现场所得,见表1。

表1 机理预测模型系数

综上,热连轧出口板凸度的机理预测模型表达式为

C=1.244×10-5·P-2.172×10-5·F+

0.003 61(ωH+ωW)-0.036 4

(3)

在轧制过程中,由于轧辊内部存在的不均匀温度场而产生不均匀热膨胀,轧辊热膨胀导致的轧辊热变形会影响板带钢的板凸度,轧辊热凸度通过以下公式[17]进行求解:

(4)

(5)

式中:βt为轧辊的热膨胀系数;ν为轧辊的泊松系数;T(r,z)为坐标位于(r,z)处的温度;T0(r,z)为轧辊初始温度;ΔL为带钢在温度变化为ΔT时的热膨胀量;L为膨胀前的长度。

在实际热轧生产过程中,轧辊和轧件的热量传递、温度分布较为复杂且不易精准确定,为了使模型简化处理,近似将轧辊温度看作均匀分布,因此轧辊热凸度表达式如下:

ωH=(1+ν)βt·R·ΔT

(6)

随着热连轧过程的不断进行,轧制长度不断累加,轧辊磨损也处于一个变化与积累的过程,加速轧辊磨损程度,直接影响着带钢板凸度。但轧辊磨损很难从机理上推导出精准公式,通常采用现场经验来建立模型,经由下述轧辊磨损量的经验公式[18]进行求解:

wn=k∑Pin·lin(1+αX4)/w

(7)

(8)

式中:wn为轧辊磨损量;Pin为第n架轧机轧第i卷钢时的轧制力;w为带钢宽度;lin为第n架轧机轧第i卷钢时的轧制长度;k为与轧辊材质和带钢材质有关的系数,根据实际生产现场选定k=0.001 3;α为轧辊磨损系数,与轧制带钢长度、轧制力、轧辊材质有关,可在[0.000 4,0.006]区间内进行人工设定,选定α=0.006;lin、bin、hin分别为第n架轧机轧第i卷钢时的轧后长度、宽度、厚度;Ln、Bn、Hn分别为带钢轧前长度、宽度、厚度。

当X=0时,对应带钢中心线处,此时,w0=k∑Pin·lin/w;当X=±1时,对应带钢边部,此时,w1=k∑Pin·lin(1+α)/w。

轧辊磨损凸度表示为

ωW=w0-w1=-0.001 3α∑Pin·lin/w

(9)

2 热连轧板凸度数据驱动模型

2.1 生产数据的采集与预处理

以国内某钢铁企业1 100 mm热连轧生产线为本文背景,该生产线能够生产常见钢种的带钢,并配备相对应的测量设备。将实际热连轧现场的生产数据存入轧制过程数据库,对历史数据做适当预处理用于训练数据驱动模型并保存,再将当前数据输入训练好的模型并进行板凸度预测,将预测结果储存板凸度预测数据库中并用于现场生产。预测过程见图1。

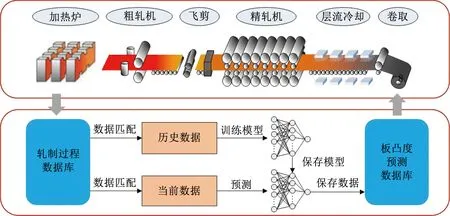
图1 热连轧出口板凸度预测过程

综合考虑板凸度机理以及实际生产现场,板凸度受多方面因素的影响,主要与轧制过程中的轧辊、带钢尺寸以及轧制条件有关,轧辊状态主要包括轧辊温度、表面状况、轧辊热膨胀以及轧辊磨损等方面,对辊缝产生影响进而影响热连轧板凸度的变化;带钢尺寸主要包括带钢厚度、宽度以及材质等物理特性,通过影响轧制力和轧机弹跳进而影响热连轧板凸度;轧制条件主要包括轧制力、弯辊力、轧制速度、轧制温度等方面,其中轧制温度会影响带钢变形抗力进而改变轧制力能参数导致热连轧板凸度的变化,而轧制速度会直接影响轧制力与辊缝使热连轧板凸度产生影响。根据轧制过程中的实测数据与过程自动化级的计算数据,为使得最终训练后模型的鲁棒性强且泛化性好,选取了10种影响因素作为板凸度预测的输入变量,影响因素的描述见表2,其中以轧辊热膨胀量与轧辊轧制长度反映轧辊热凸度与磨损凸度的变化规律进而反映轧辊状态,以带钢厚度、宽度、变形抗力反映带钢尺寸状态,以轧制力、弯辊力、轧件入口温度和出口温度、轧件速度反映轧制条件。并从该厂采集八机架连轧板带钢的在线数据,分析热连轧生产线相应的PDA数据,并提取数据共计1 797组。

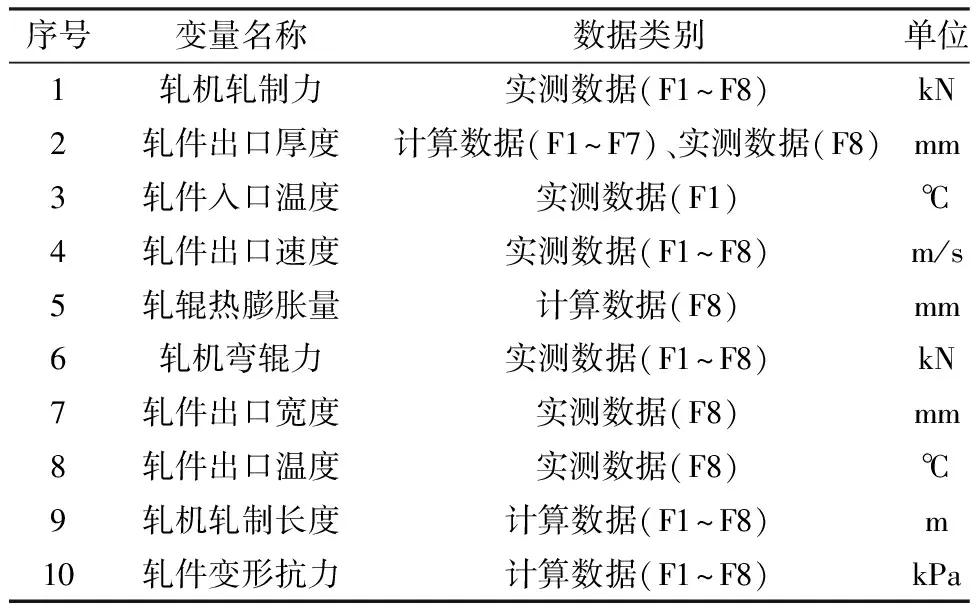
表2 热连轧出口板凸度的影响因素

以热连轧板凸度的影响因素中的轧机轧制力、轧机弯辊力、轧件出口厚度以及轧件出口宽度为例构建数据三维可视化图像。在图2中,数据的可视化图像显示了影响热连轧出口板凸度的变量的分布,其呈现出无序化分布,由此可得,数据量大的同时也具有明显的无序性与分散性,可部分证明在实际生产中使用数据集开发的模型具有较强的鲁棒性。

由于实际热连轧生产过程中所得到的原始数据大多可能包含少量会产生误导性预测的噪声和异常值,因而为保证所采用的数据集具有客观性与真实性,在模型建立与预测时能够获得可靠的分析结果,必须在使用数据之前先对其进行预处理。

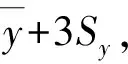
(10)

(11)

(12)

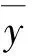
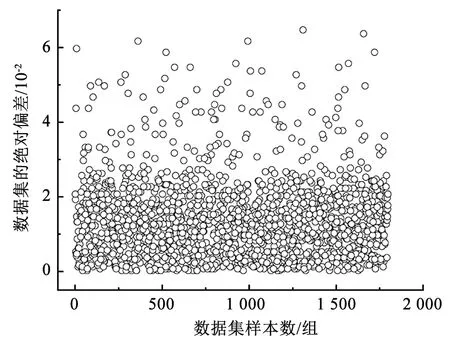
图3 基于PauTa准则去除异常值

同时,不同的评价指标往往具有不同的维度,为了消除维度带来的影响,需要对处理后的数据集进行标准化处理。本文通过Min-Max归一化的方法将数据的平面分布扩展为类圆形分布,即为将数据进行线性变换,使得结果映射为0和1之间的值,以便消除数据量级之间的差异,公式如下:

(13)

再选取其中70%(约1 247块)作为训练集,用于训练网络并调整网络的参数,选取其中的30%(约535块)作为测试集,用于测试训练后的神经网络对热连轧板凸度预测的性能,测试模型的准确性。部分试验数据见表3。

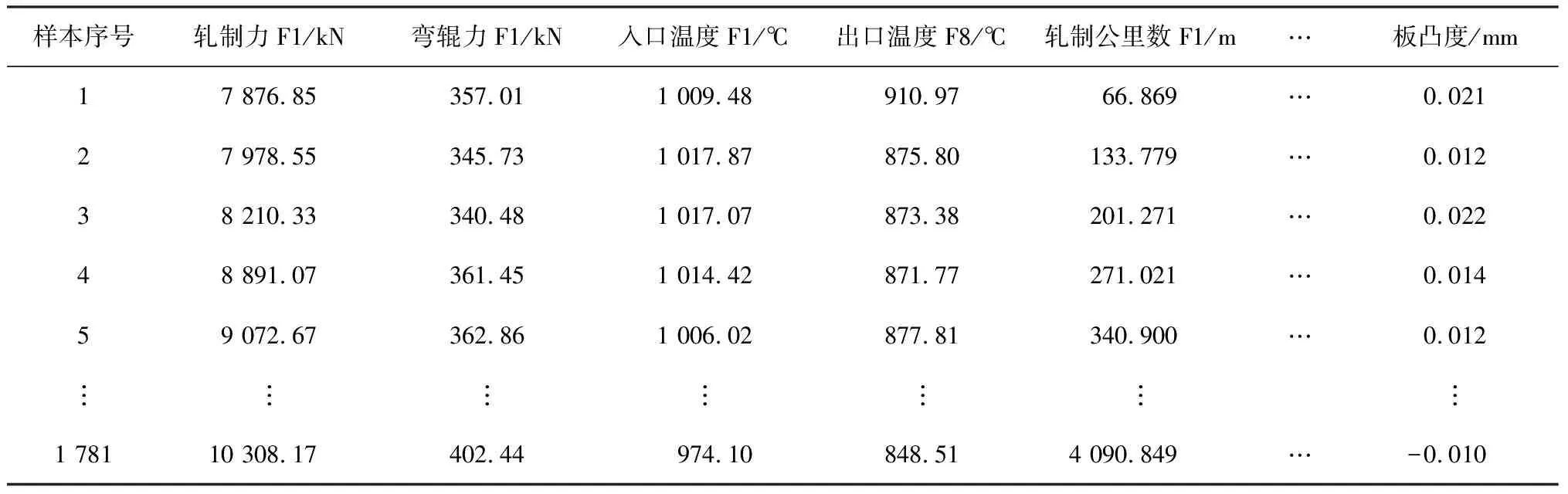
表3 部分实验数据

2.2 数据驱动模型

深度神经网络(deep neural networks,DNN)又名多层感知机(multi-layer perception,MLP),从DNN按照不同层级的位置划分,其内部的层级可以分为输入层、隐含层以及输出层。图4为DNN的结构图,由图4可知,在神经网络中,各个层级之间是全连接的,即任意一层中的任意一个神经元皆与前后两层的神经元相连接。不同于单隐层神经网络,DNN增加了隐层数量,因此DNN通过深层结构能够从训练数据中学习一些复杂的非线性关系,从而实现对复杂数据分布的逼近,进而解决复杂问题。模型所采用的隐含层结构为“50-50-50”。选Sigmoid激活函数,采用均方差来度量损失,在确定损失函数后,选用Lookahead优化器算法[19]来更新和计算影响模型训练和模型输出的网络参数,选择不等间隔退火策略的余弦退火算法[20]来调节模型学习率。

图4 深度神经网络DNN结构

随机配置网络(stochastic configuration network,SCN)[21]具有对回归和分类分析的强大功能。图5为DNN的结构图。传统上,正确确定神经网络的适当架构是非常具有挑战性的,以便培训的模型可以实现学习和泛化的优异性能。与单隐式层前馈神经网络的已知随机学习算法相比,SCN随机分配隐藏的输入权重和偏差在监督机制中的节点。由于隐藏层中的参数在均匀分布中随机产生,因此假设有最佳的随机性。SCN中权重和偏差的随机化值是在序列Lambdas=[0.5,1,5,10,30,50,100,150,200,250]对应的[-λ,λ]的范围内选择的,该扩展范围设置允许更大的范围,可以找到满足不等式约束的合适权重和偏差。此外,设置收缩因子为[0.9,0.99,0.999,0.999 9,0.999 99,0.999 999]。针对每个已知候选项的不等式约束进行测试的随机值池大小为250,迭代节点的最大数量选择为150。

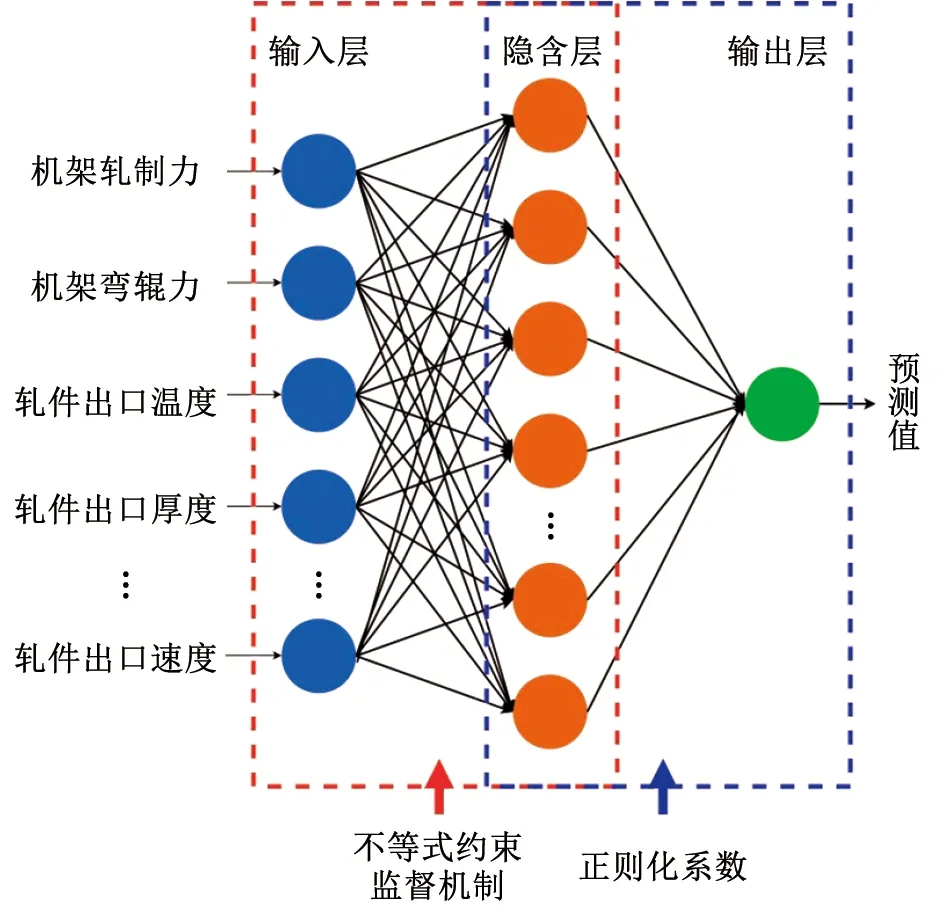
图5 随机配置网络SCN结构

2.3 热连轧板凸度组合预测模型

在传统热连轧出口板凸度的预测过程中,直接将板带钢凸度作为神经网络的输出值,仅依靠神经网络进行参数预测,其预测产生的误差范围较大,模型的预测精度降低,且与实际物理原理贴合度不够,可说服性、解释性低,因此提出一种将机理与神经网络模型相结合的热连轧出口板凸度组合预测模型,以求得的机理预测模型计算值设定为热连轧出口板凸度的基准值,该基准值与实际值的数量级接近,而二者间偏差的波动范围相比之下较小,由此向模型中引入偏差量的概念,即热连轧出口板凸度基准值与生产线实测数据的差值,以热连轧出口板凸度偏差量作为神经网络模型的输出变量进行预测,再将偏差量预测值与基准值相加得到组合预测模型的板凸度预测值,以此对传统热连轧出口板凸度预测模型进行修正,具体预测过程见图6。

图6 组合预测模型原理

在建立热连轧出口板凸度组合预测模型后,对热连轧出口板凸度的偏差量进行预测,再将该偏差量的预测值与热连轧出口板凸度的基准值进行求和,得到机理与数据驱动模型结合后的热连轧出口板凸度组合预测模型的预测值。

3 效果分析及验证

通过将数据导入本文提出的热连轧板凸度组合预测模型,经由性能指标均方误差MMSE、平均绝对误差MMAE、均方根误差RRMSE、对称平均绝对百分比误差SSMAPE以及相关系数R,对比评估预测结果,表达如下所示:

(14)

(15)

(16)

(17)

(18)

分析模型的预测指标,基于DNN的组合预测前后的预测结果见图7,基于SCN的组合预测前后的预测结果见图8,数据点清晰、规则地分布,可以由此看出相比于传统的数据驱动模型,数据驱动与机理相结合引入偏差量这一概念后,数据分布更集中于对角线,误差更小,性能更好。基于DNN的热连轧出口板凸度组合预测模型的预测性能见图9,基于SCN的热连轧出口板凸度组合预测模型的预测性能见图10,通过不同颜色标识对绝对误差进行分级;当颜色由黑色到灰色,绝对误差从0增加到0.02 mm,当颜色为白色时,则表示绝对误差超过0.02 mm,对于更高的生产要求,测量值和目标冠之间的绝对误差预计<0.02 mm,甚至<0.01 mm。对于基于DNN的热连轧出口板凸度组合预测模型,有97.96%的预测数据绝对误差<0.02 mm,有82.59%的预测数据绝对误差<0.01 mm。对于基于SCN的热连轧出口板凸度组合预测模型,有99.07%的预测数据绝对误差<0.02 mm,有85.19%的预测数据绝对误差<0.01 mm,符合实际生产要求。

图8 基于SCN的组合预测前后预测结果对比

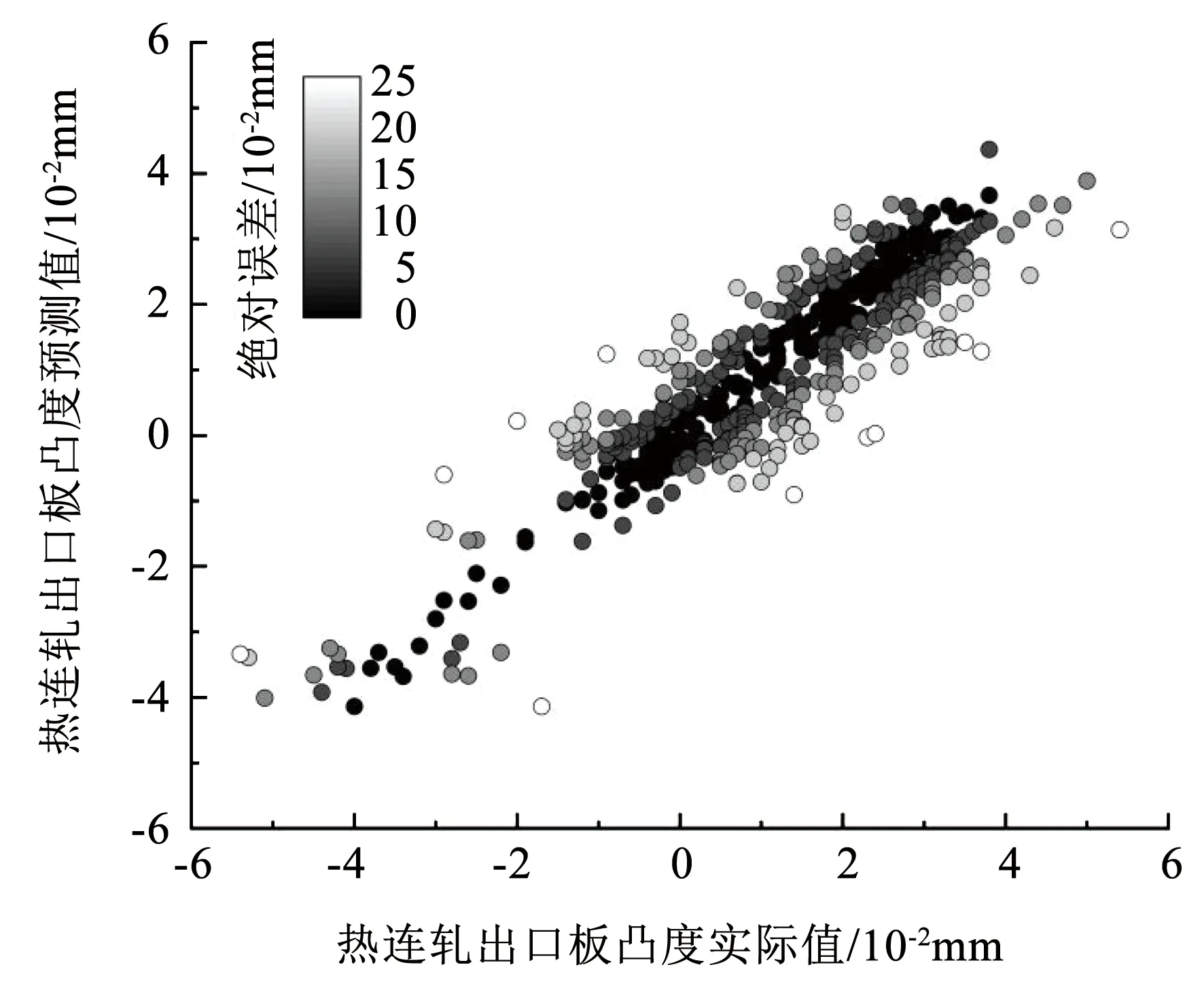
图9 基于DNN的组合预测模型预测性能

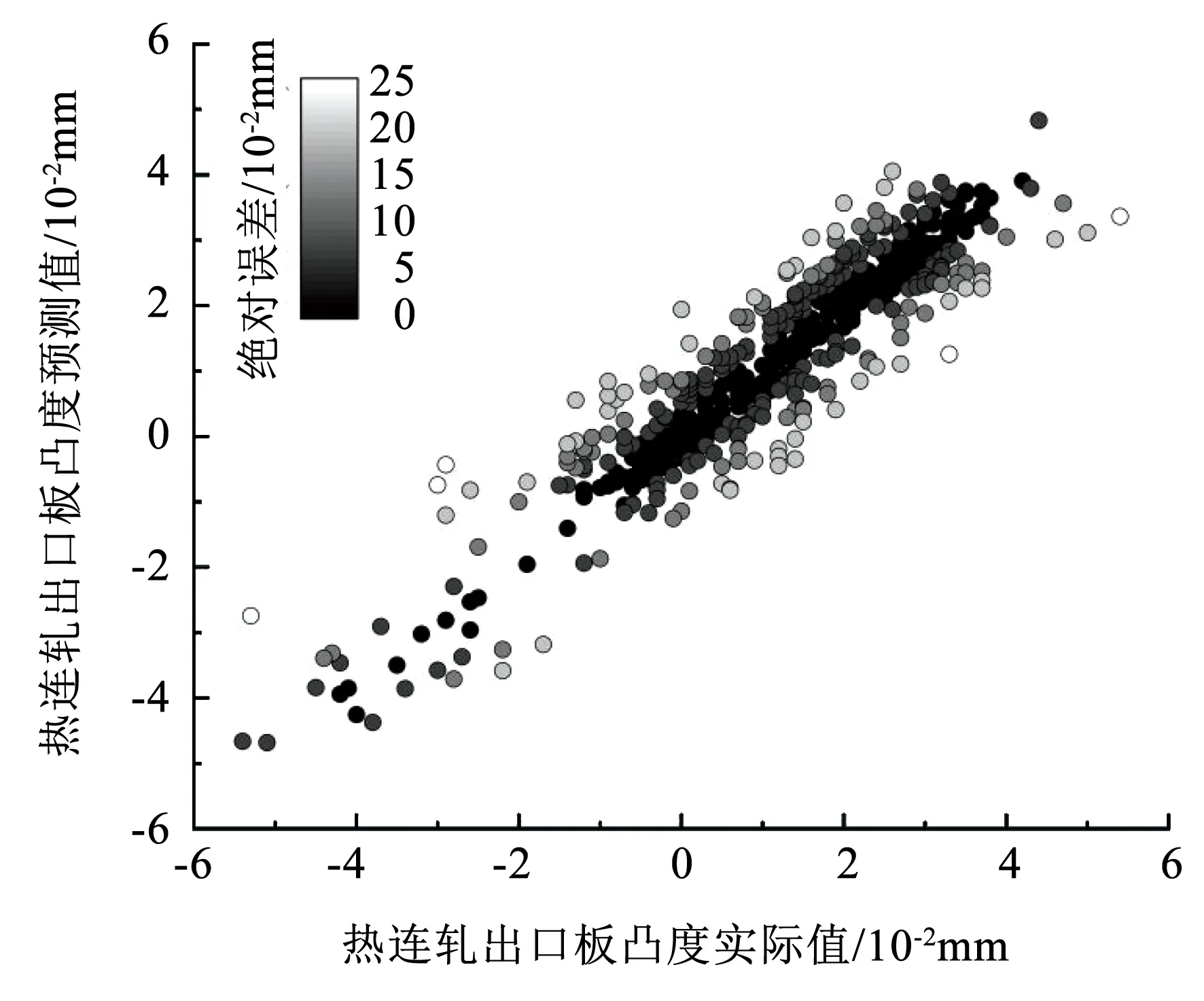
图10 基于SCN的组合预测模型预测性能

由图11及表4可以看出,相比于直接预测板凸度、直接采用数学模型预测板凸度的这两类模型,以引入偏差量的方式进行数据驱动与机理相结合所建立的基于DNN的组合预测模型的MMAE、SSMAPE和RRMSE等误差指标的值显著降低,MMAE、SSMAPE和RRMSE值分别为0.004 7 mm、53.25%和0.006 2 mm。充分证明了所提出的以偏差量的形式进行数据驱动与机理相结合后的热连轧出口板凸度模型对提高板凸度预测精度具有有效性。分别采用DNN与SCN对该组合预测方法进行建模,对比组合预测前后的误差指标,对于上述2个网络该组合预测模型精度均优于直接预测板凸度的模型,部分证明了该方式具有可行性与普适性,同时更贴合于实际物理过程。

图11 板凸度预测误差直方图

表4 预测模型误差指标

4 结 论

1)热连轧板凸度机理与数据驱动组合预测模型通过神经网络对偏差量进行了修正,使预测误差进一步降低,其中有97%以上预测数据的绝对误差<0.02 mm,有82%以上预测数据的绝对误差<0.01 mm。

2)将基于DNN的热连轧板凸度组合预测策略应用至SCN,结果表明,基于SCN的组合预测模型精度比传统SCN模型的SSMAPE降低了6.51%,R提高了5.94%,证明了本文所提出的组合策略具有有效性以及普适性。

3)热连轧板凸度机理与数据驱动组合预测模型有效改善了传统机理模型难以准确求解、传统数据驱动模型学习特征不完全等缺点,在提高模型预测精度的同时也使其更加符合实际物理意义。