股价波动持续性与反转收益
张 燃, 陈少霞
(北京科技大学 经济管理学院, 北京 100083)
一、问题的提出
资本市场作为重要的要素和资源市场,是现代金融体系的核心组成部分。党的二十大明确指出,健全资本市场功能,提高直接融资比重,进一步彰显资本市场在市场资源配置中的关键作用。然而,由于市场流动性偏低、投资者结构不合理等因素,我国资本市场发展尚不平衡,并表现出种种“异象”,严重制约了市场功能的发挥。特定时期,股票价格持续波动,引发投资者情绪的广泛波动,对金融市场稳定构成一定威胁。由此可见,对中国股票市场“价格异象”成因的讨论具有重要的现实意义,有助于深刻理解资本市场运行规律,守住不发生系统性风险底线。
动量效应和反转效应是资本市场最常见的“异象”之一,即股票过去的价格会对未来价格具有预测能力。Jegadeesh &Titman[1]等的研究较早地发现了国际资本市场普遍存在动量和反转特征,投资者利用上述特征可以获得可观的收益。动量和反转效应受到了学术界的持续广泛关注,传统的金融理论以及前沿的行为金融理论都对上述现象给出了诸多解释。值得一提的是,随着对动量和反转效应的深入探索,行为金融学的理论体系逐渐完善,产生了正反馈交易假说、保守偏差及代表性偏差、过度自信等一系列理论,对资本市场“价格异象”的解释日益深刻。基于风险视角的阐释是传统理论分析的延伸,这类文献将收益的持续性与风险的持续性联系起来,证实了回报率的可预测性源于风险的可预测性[2]。随着学术界对金融市场价格风险的研究取得里程碑式的进展,即利用自回归条件异方差(ARCH)模型[3]及广义自回归条件异方差(GARCH)模型[4]刻画股票回报率的波动聚束(聚集)现象①,对收益持续性与风险持续性的研究逐渐深入。资产价格波动的持续性可能会由很多原因导致。例如,影响资产价格的信息披露过程是逐步完成的;又如,市场参与者对信息的感知亦随着时间的变化由浅及深,并逐渐调整其决策行为。当资产价格的波动表现出长持续性时,风险溢价的惯性或许会更为强劲。那么,资产价格的波动持续与动量效应或反转效应是否存在某种关系,这种关系是否相辅相成,对上述问题的回答有助于从全新的视角探索动量效应或反转效应的形成机理。
需要注意的是,中国和美国的股票市场存在巨大差异,因此不能以国外文献的经验做法直接套用于处理中国市场。与美国相比,中国股票市场散户投资者占比大②,换手率高③,交易行为易受投资者情绪影响,动量效应在中国A股市场总体表现不佳[5-8]。同时,在一个换手率极高、短期动量不足的市场中,波动持续性对股票回报率的影响可能会有独特的表现,但已有文献在上述领域尚存空白。基于此,本文以2005—2021年我国A股市场上市公司作为研究对象,实证检验了股价波动持续性与股票预期收益之间的关系,以及波动持续性对动量效应或反转效应的影响。具体而言,与陈淼鑫、黄振伟[9]基于GPH估计法滚动测算我国股票长记忆性的研究不同,本文针对个股回报率建立EGARCH模型,用“GARCH系数”的绝对值度量股价波动持续性,根据股价波动持续性大小将样本分组,并建立投资组合检验股价波动持续性与预期收益在时间序列上的关系;同时,通过混同横截面回归研究股价波动持续性对未来个股回报率的解释能力。在此基础上,对中国A股市场动量效应和反转效应的特征事实进行识别,根据股价波动持续性与股价过去表现进行分组,研究股价波动持续性与动量或反转效应之间的关系④,并利用GARCH 模型对股价波动持续性的测算结果进行稳健性检验。
本文通过对波动持续性与股票回报率关系的实证检验,从波动持续性的角度阐释了中国A股市场存在“反转效应”的原理,对认识中国股票市场风险持续性和收益持续性的关系提供了全新视角,具有一定的理论价值。同时,正如前文所述,本文的研究对了解资本市场运行规律、提升投资组合业绩和风险管理效果都具有重要的实践意义。
二、文献综述
(一)股价波动率与股票预期回报的关系
关于股价波动率与预期回报之间的早期研究只考虑系统性风险的影响,认为个股回报率与波动率正相关。Ang et al.[10]借助Fama-French三因子模型计算个股特质波动率,指出特质波动率更高的股票在未来预期收益更低,该现象又被称为“特质波动率异象”。上述发现打破了传统理论的解释框架,在资产定价的实证研究领域引起较为激烈的讨论。Fu[11]等则提出了相反的看法,他们认为Ang et al.[10]发现的负相关性源于样本中少量的高特质波动率股票的回报率反转效应以及特殊时期极端值的影响。在剔除极端值以后,特质波动率和回报率之间依然是正相关关系。事实上,特质波动率与预期回报率之间的关系会受到多种因素的影响,因此很难有定论[12]。
Bali et al.[13]和Hou &Loh[14]的研究都发现,投资者对“彩票型股票”的偏好是“特质波动率异象”的一个主要原因。较高的特质波动率常常被视为有碍套利的因素之一。基于这一出发点,Stambaugh et al.[15]从套利风险和套利不对称性两个角度对“特质波动率异象”之谜进行了研究,建立了特质波动率、套利风险以及错误定价三者之间的联系,并认为特质波动率高的股票,套利风险也高,因此错误定价难以被消除。套利不对称性造成高估值股票中特质波动率和回报率的负相关强于低估值股票中特质波动率和回报率的正相关,因而导致截面上出现特质波动率和回报率的负相关现象。Cao et al.[16]则发现,特质波动率异象存在显著的“日历效应”,特质波动率与下一个月回报率的负相关性主要出现在当月的第三周。
也有部分学者认为,股票价格中并不包含股票的异质性风险。例如,Brockman &Yan[17]发现,特质波动率呈现随时间逐渐降低的趋势,等权重加权或市值加权的特质波动率均不会对市场收益产生影响。针对中国资本市场的研究则发现,中国股票市场的异质性风险与未来股票收益之间存在负相关关系[18]。
(二)动量效应和反转效应的影响因素
学术界对动量效应、反转效应的理论阐释主要有两类主流视角,第一类基于传统金融理论框架,第二类基于行为金融学框架。针对Jegadeesh &Titman[1]提出的“完善动量策略所获得的超额收益无法由系统性风险解释”问题,传统金融理论将股票的超额收益归因于风险溢价,认为执行动量策略所获得的超额收益是对随时间变化的风险的合理补偿[19],“价格异象”并不能证明市场是非有效的,可能是由于经典模型并没有包含所有的风险因子,才导致超额收益的存在。市场有效论的支持者一直在尝试寻找新的风险因子来解释动量效应或反转效应,但尚未形成统一的框架。同一个模型在不同的国家、不同的时期也会得出不一致的结论。对“价格异象”基于风险时变性的阐释认为,时变风险因子是出现动量效应或反转效应的主要原因。这种观点强调,“价格异象”反映了市场参与者对宏观风险预期的时变性。例如,Johnson[20]认为,偶然发生的持续红利冲击可以解释包括“动量效应”在内的很多异象;Pastor &Stambaugh[21]分别从流动性风险和增长期权风险的时变特征出发阐释了动量(反转)策略有效性的内在机理。
行为金融学相关理论给出了截然不同的解释。大量文献指出,投资者受到认知水平、情绪和心理等因素的影响,在决策时会表现出有限理性。基于此,行为金融学派对“价格异象”的探索不断拓展,理论体系逐渐完善。例如,正反馈交易假说认为,前期价格上涨或下跌的股票会在投资者“追涨杀跌”的正反馈交易中继续上涨和下跌[22];保守偏差及代表性偏差的分析视角则指出,保守偏差会造成反应延迟,代表性偏差会进一步加剧资产价格对其真实价值的偏离程度,两种偏差行为引起的反应不足是导致动量(反转)效应产生的主要原因[23]。还有观点认为,投资者对私有信息的“过度自信”及随后的“过度反应”引起股票价格持续的上涨或下跌。Hong &Stein[24]进一步将投资者分为信息观察者和动量交易者,并以此为基础解释了资本市场中的过度反应、反应不足与动量和反转效应之间的关系。Lee &Swaminathan[25]通过研究动量策略的长期表现发现,至少有一部分惯性收益来源于延迟的过度反应。
对中国股票市场动量效应或反转效应的相关研究主要聚焦特征识别和原因解释。特征方面,白颢睿等[5]强调,中国是一个动量效应不足的市场。虽然也有学者提供了中国股票市场存在短期动量效应的证据,但上述动量效应并不稳定。对“价格异象”成因的解释普遍聚焦中国独特的市场环境、监管制度和投资者结构等因素。已有文献指出,由于我国股票市场的换手率高、噪声交易严重,反转效应比动量效应更加明显。动量效应或反转效应受到如不同的形成期和持有期、换手率,以及估计模型的差异[26]等诸多因素的影响;此外,彩票型特征会减弱动量效应[27]。
(三)文献述评与本文的边际贡献
回顾上述文献不难发现,尽管国内外学者较为全面深入地探索了股价波动率与股票预期回报之间的联动关系,但鲜有文献关注到股票波动持续性对动量效应或反转效应的影响,针对上述文献空缺,本文进行了创新性探索。与已有文献相比,本文的边际贡献主要体现在:从风险时变性视角对中国股票市场的反转效应给出了解释,丰富了股价波动持续性和股票价格异象的文献研究范畴;同时,本文通过波动持续性与动量效应和反转效应的联系,给出了“优化投资组合,获得超额收益”的全新思路,将为后续文献的基础策略设计提供经验参考。
三、研究设计
(一)研究思路
股价波动持续性聚集过去回报率方差对未来回报率方差产生持续的影响。目前,对股价波动持续性的估计方法有非参数估计法、半参数估计法和参数估计法。非参数估计方法主要包括重标极差及其修正方法和去趋势分析法等。利用非参数估计方法,能够得到一个对时间序列持续性的检验结果,从而判断序列是否存在持续性,但难以进行具体的持续性大小比较,无法了解估计量的统计性质,因而不适用于本文的研究。半参数估计方法包括GPH法和局部Whittle估计方法等。半参数估计方法适用于弱假设条件的情形,实际操作比较复杂。参数估计方法能够充分利用市场数据还原真实结果,得到波动持续性的估计量,相关模型尤其以Bollerslev[4]为代表的GARCH族模型见长。模型由均值方程或波动率方程共同构成,能够刻画金融市场数据的异方差性。
越来越多的研究表明,在美国股票市场和中国股票市场均存在显著的波动持续性,GARCH族模型可以有效描述中国A股市场的个股波动性。模型中条件方差的自回归系数反映了当前条件方差的波动性对未来条件方差的影响程度,可以作为波动持续性的度量。其中,EGARCH模型考虑了非对称效应,允许在模型中体现正负资产收益率对波动率的非对称影响。本文采用EGARCH (1,1)模型来估计股价波动率及波动持续性。方程具体形式如下:
Ri,t=ut+at
(1)
at=σtεt
(2)
(3)

根据波动持续性的定义,本文使用方程(3)中GARCH项系数β1的绝对值来度量股价波动持续性。β1的绝对值越大,表明该时间序列的波动持续性越大,此时过去的波动对未来波动的影响越大;β1的绝对值越接近0,表明该时间序列的波动持续性越小,此时过去的波动对未来波动的影响越小。
(二)样本选取和数据来源
本文以中国发展最成熟和最具代表性的沪深A股市场的股票作为研究对象,考察股价波动持续性对预期收益和动量/反转效应的影响。本文的样本区间设定为2005—2021年。本文将研究期间设置在2005年以后主要基于两方面的考虑:一方面,为了保证研究期间内有足够的样本观测值;另一方面,文中被作为市场组合的沪深300股票指数是在2005年推出的。
基于研究需要,本文依次对由全部A股上市公司构成的初选样本做如下筛选:为了避免新股发行后股价剧烈波动干扰研究结果,参照Liu et al.[28]的做法,本文删除了新股上市后首个半年的交易数据;由于金融行业的特殊性,本文参照宫汝凯[29]等的做法,将银行等金融类上市公司排除,同时排除了ST、PT等非正常交易的股票数据;为了满足流动性的需要,本文删除了年内交易天数不足150天的当年所有观测值。最终,参与实证研究的上市公司有4 036家。本文实证研究用到的个股日收益率数据和月收益率数据以及公司基本面数据来自CSMAR和Wind数据库。
(三)描述性统计
本文首先使用个股日收盘价计算个股的对数收益率。选取每只股票每半年的收益率时间序列数据建立EGARCH (1,1)模型,共得到了57 228个波动持续性观测值。表1是依据EGARCH (1,1)模型建模的回归结果。从表1可以看到,GARCH项系数β1的均值为0.510 8,中位数为0.513 8,标准差为0.295 0。本文在后续的实证分析过程中剔除了GARCH系数为0的观测值(占总观测值的比例为0.86%)。

表1 股价波动持续性指标的描述性统计结果
在进行混合数据的回归时,本文还将用到部分关键解释变量,即股价波动持续性之外的变量。本文选择可能对股票价格和回报率产生重要影响的变量作为控制变量,包括公司规模(Size)、账面市值比(BM)、动量特征(Mom)、特质波动率(IVol)、股票流动性(Illiq)、彩票特征(Max)和资产收益率(Roe)等。具体而言,公司规模(Size)以个股上年年末流通市值的自然对数值度量,账面市值比(BM)为个股年报中每年年末的账面市值比实际值,动量特征(Mom)以个股当年12个月的累计超额收益率度量。用股票每月的日超额收益率对Fama-French三因子回归,回归残差项的标准差即为特质波动率(IVol)。股票流动性(Illiq)用每个月内N个交易日的日收益率绝对值与当日成交额比值的平均值来度量;彩票特征(Max)以个股每个月的最大日收益率来度量;资产收益率(Roe)以个股每年年末的净资产收益率来度量。控制变量的统计特征详见表2。

表2 控制变量的描述性统计结果
四、实证结果与分析
为了检验波动持续性与股票未来收益之间的关系,本文首先参考 Jegadeesh &Titman[1]的研究,构建动量(反转)交易策略,根据股价波动持续性大小将样本分组,在每组内构建反转策略多空组合,观察不同组内反转策略的收益,以此检验股价波动持续性与预期收益在时间序列上的关系。在此基础上,通过混同横截面回归研究股价波动持续性对未来个股回报率的解释能力。
(一)基于单变量分组的时间序列分析
为了探讨股价波动持续性与股票预期回报率之间的关系,本文首先采用单变量分组方法进行投资组合分析。投资组合分析的实质是按照某一指标对股票进行排序和分组,构建投资组合并持有一定的时期。然后,计算投资组合在持有期内的收益,比较不同投资组合的超额收益是否具有显著差异,从而检验该指标对股票收益的影响。与线性回归分析相比,投资组合分析法既能减少线性假设的限制,也能避免个别极端值的影响。
具体地,在每个月依据股票过去半年的股价波动持续性指标进行排序,将样本平均分为5组,第一组由波动持续性最小的20%股票构成,记为L组合;将波动持续性最大的20%股票构成的组合记为H组合;中间各组标号依波动持续性由小到大分别记为2、3和4;同时,买入波动持续性较小的股票组合并卖出波动持续性较大的股票组合,即做多L组合并做空H组合,记为L-H组合。每半年进行一次调仓,计算L-H组合在不同持有期内的平均超额收益,投资组合收益率采用流通市值加权法计算。如果最终L-H组合的收益显著,则证明波动持续性能够预测股票的未来收益。
事实上,多空组合L-H的收益率可以视为波动持续性因子的收益率。这是因为,收益率均值可能会受到样本区间和其他因子变化的影响,学术界更加关心因子在风险调整后是否具有显著的风险溢价。更科学的方法是,考察控制其他风险因子以后的风险溢价,惯常的做法是使用CAPM模型或者Fama-French三因子模型作为风险调整的基准模型[30]。本文将各投资组合收益率和市场因子收益率分别代入CAPM模型和Fama-French三因子模型当中,回归截距项代表投资组合经过风险调整后的风险溢价。
表3报告了样本期内每个分组投资组合的超额回报率。R是投资组合回报率减去无风险利率之后的平均值,αCAPM和αFF分别由CAPM模型和Fama-French三因子模型计算得到。CAPM模型和Fama-French三因子模型中涉及的市场因子为沪深300指数回报率。可以看到,随着波动持续性的增大,投资组合的平均回报率呈现逐渐降低的趋势。其中,当持有期为6个月时,L组的超额回报率为12.434 5%,H组的超额回报率为9.712 5%,L-H组合的回报率为2.722 0%,多空组合的回报率在1%的水平下显著为正,说明股价波动持续性与股票预期超额回报之间存在显著的负相关关系,股价波动持续性越大的股票,预期回报率越低。进一步考虑CAPM市场因子和Fama-French三因子的影响后,αCAPM和αFF依然呈现从低波动持续性组合到高波动持续性组合逐渐降低的趋势,并且L-H多空组合的异常收益均显著为正。这说明,股价波动持续性与其预期收益之间的负相关关系无法由CAPM市场因子或Fama-French三因子完全解释。

表3 按照波动持续性分组的投资组合超额回报率
此外,假设不考虑卖空限制,L-H多空组合的收益率显著为正,这意味着波动持续性小的股票比波动持续性大的股票在6个月内可以多获得2.722 0%的收益。即使在CAPM模型和Fama-French三因子模型中,该组合仍可以赚取正的收益。这同样说明,波动持续性小的股票预期回报显著高于波动持续性大的股票,证明了二者之间存在稳健的负相关关系。
(二)混同横截面回归分析
为了进一步探索股价波动持续性与个股预期回报关系的横截面特征,本文接下来采用混同数据回归分析方法进行估计。对所有股票在控制年份后进行回归,方程如下。
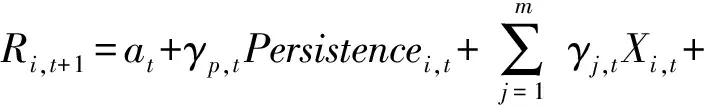
(4)
其中,被解释变量Ri,t+1是股票i在未来6个月内的月平均超额收益率,月平均超额收益率以个股月收益率减去沪深300指数月度回报率来度量。Persistencei,t是股票i在t月(用过去半年的日度数据计算)的波动持续性,以GARCH项系数来度量。ε是回归方程的残差项。X是代表公司特征的控制变量,如前文所述包括公司规模、账面市值比、动量特征、特质波动率、股票流动性、彩票特征和资产收益率等。
根据表4的实证结果,在列(1)中,波动持续性对预期收益的影响是-0.003 9,即在截面上,波动持续性的回归系数为-0.003 9,变量在1%的水平下显著,再次验证股票预期收益与波动持续性呈负相关关系。在列(1)的基础上逐渐增加公司特征作为控制变量,波动持续性的影响都在1%的水平下显著,且系数为负。在包含所有控制变量的列(8)中,方程对预期收益的解释力为22.00%,波动持续性在1%的水平下显著,且系数为负。总而言之,通过回归结果可以看到,在控制了公司规模、动量特征、股票流动性和年份等因素以后,波动持续性与未来股票收益依然存在显著的负相关关系。

表4 波动持续性影响预期收益的混同横截面回归结果
综上所述,就中国A股市场而言,无论在投资组合层面还是在个股层面,股价波动持续性与股票预期收益之间均存在显著的负相关关系,股价波动持续性能够有效预测股票收益。一种可能的解释是,股价波动持续性越大意味着波动表现出更高的可预测性,减少了风险的不确定性,投资者预期的风险补偿降低,故波动持续性与预期收益呈现负相关关系。
五、进一步研究
通过以上实证分析过程不难发现,就中国A股市场而言,无论在投资组合层面还是在个股层面,股价波动持续性与股票预期收益之间均存在显著的负相关关系,股价波动持续性能够有效预测股票收益。接下来,本文将探索上述关系具体体现为动量特征还是反转特征,进而明确如何利用这一关系构建交易策略,实现投资收益。
Chordia &Shivakumar[2]和Johnson[20]等均认为,风险在市场上已经被定价,进而可以将收益的持续性与风险的持续性联系起来,解释不同策略的盈利能力。在控制其他条件的情况下,风险溢价与个股波动成正比。当波动表现出较强持续性时,风险溢价的惯性也会增强。所以,从直觉来看,在动量效应显著的市场中,波动持续性可以增大动量效应;在反转效应显著的市场中,波动持续性大的股票其反转效应更强。鉴于中国股票市场是反转效应显著的市场,本文优先研究波动持续性与反转收益的关系,并同时确认反转效应的存在性。
(一)基于无风险利率调整的反转收益
借鉴Jegadeesh &Titman[1]的方法,在每个月,根据过去半年股价计算得到的波动持续性进行排序,将样本平均分为5组,波动持续性最小的20%股票构成投资组合P1,以此类推,波动持续性最大的20%股票构成投资组合P5。对每一个股票分组Pi(i=1、2、3、4、5),在样本期的每一个月,计算组中每只股票过去6个月的平均收益率;然后按平均收益率排序,平均收益率最大的20%股票构成赢家组合,平均收益率最小的20%股票构成输家组合;接下来计算各个组合在持有期内的平均月回报率,其中赢家组合的回报率记为Rw,输家组合的回报率记为Rl;最后构建多空组合,买入输家组合并卖出赢家组合,其回报率记为ΔR=Rl-Rw。投资组合回报率采用市值流通加权法计算,本文持有期K分别选择1、3、6、9、12个月,对于每一个持有期,令:
ΔP=ΔR5-ΔR1
(5)
ΔR1=R1l-R1w-Rf
(6)
ΔR5=R5l-R5w-Rf
(7)
其中,Rf表示月度无风险利率。ΔR1表示波动持续性最小的20%股票构成投资组合P1中多空组合的月平均超额回报率。ΔR5表示波动持续性最大的20%股票构成投资组合P5的反转策略月平均超额回报率。ΔP=ΔR5-ΔR1为波动持续性差异导致的反转效应,衡量了波动持续性对反转效应的影响。如果ΔP显著地大于0,则表明波动持续性放大反转效应;反之,如果ΔP显著地小于0,则表明波动持续性减缓反转效应。
表5是实证结果,表中数据为按照算术平均方法计算的组合收益率。列(1)是针对全样本执行反转策略的结果,不同持有期的反转收益均为正,验证了样本期内主要存在的是反转效应。其余列数据是在不同波动持续性分组和不同持有期内执行反转策略的月平均收益率。这里的形成期为6个月;K代表持有期,分别为1、3、6、9、12个月。表中列(7)为波动持续性最大的组合与波动持续最小的组合的反转收益之差。实证结果表明,波动持续性大的股票相对于波动持续性小的股票更容易呈现反转效应。并且在较短持有期内,ΔP均显著大于0,而随着持有期延长,ΔP在逐渐减小,说明波动持续性放大了反转效应。应用以上反转策略构建投资组合,当持有期为3个月和6个月时,可以获得显著的超额收益。

表5 波动持续性与反转收益的实证结果
(二)基于因子模型风险调整的反转收益
为了进一步考察经CAPM模型和Fama-
French三因子模型风险调整后,是否仍能获取反转收益,本文将模型设定如下:
Rp,t=αp+βpMKTt+εp,t
(8)
Rp,t=αp+βpMKTt+γpSMBt+ηpHMLt+εp,t
(9)
其中,Rp,t为组合回报率,根据上式中的截距项检验ΔP、ΔR1、ΔR5的显著性。MKT为市场超额收益率,即沪深300指数回报率减去无风险利率,SMB为规模因子,HML为价值因子,因子数据来源于CSMAR数据库。
表6中的组合回报率采取算术平均方法计算。经CAPM模型或三因子模型风险调整后,依然存在波动持续性所带来的显著的反转收益。

表6 经风险模型调整后波动持续性与反转收益的实证结果
以上结果表明,波动持续性会放大反转收益:波动持续性越大的股票,由于波动可预测性越强,收益的可预测性也越强,反转效应表现出更强的负惯性。
六、稳健性检验
为了检验上述实证结果的稳健性,本文更换估计方法,采用GARCH (1,1)模型估计的GARCH项系数度量股价波动持续性并重复以上实证分析过程。
(一)时间序列分析
表7中L组依然是波动持续性最小的20%股票构成的投资组合,H组是波动持续性最大的20%股票构成的投资组合,L-H为买入波动持续性最小组同时卖出波动持续性最大组的多空组合。与前文结论相似,不同投资组合的平均收益、CAPM模型和Fama-French三因子模型的收益都随着波动持续性的增大而减小。持有期为1个月时,L-H组合的三类收益都显著为正,其中L-H组合的收益为1.026 5%,在5%的水平下显著;经CAPM风险模型调整后达到1.070 8%,在5%的水平下显著;经Fama-French三因子模型调整后的收益为1.175 7%,在1%的水平下显著。上述结果再次验证,股价波动持续性与股票预期收益之间存在显著的负相关关系,且这种负相关关系无法被因子模型完全解释。

表7 按照波动持续性分组的投资组合超额回报率的稳健性检验结果
(二)混同横截面分析
表8是混同横截面数据回归分析的稳健性检验结果。与前文结论相似,波动持续性指标对收益率的影响均显著且系数为负。模型整体显著,说明波动持续性指标中包含公司特征因素之外的重要定价信息,股价波动持续性与横截面股票预期收益之间存在显著的负相关关系。

表8 混同横截面回归分析的稳健性检验结果
(三)波动持续性与反转收益的关系
表9是波动持续性与反转收益之间关系的稳健性检验结果。总体来看,波动持续性越高、持有期越短时,越容易出现反转效应。并且,不同持有期的ΔP显著大于0,随着持有期延长,ΔP在逐渐减小,即股价波动持续性可以放大反转效应并随着持有期的延长而逐渐减弱。

表9 波动持续性与反转收益关系的稳健性检验结果
此外,本文还计算了波动持续性与经过风险模型调整后反转收益的关系⑤。研究发现,在不同持有期内ΔP的收益率显著大于0,同样证实了波动持续性放大了股票的反转效应。随着持有期的延长,反转收益逐渐变小。
七、研究结论与政策建议
行为金融学曾提出反应不足、反应过度、正反馈假说等理论来解释动量效应和反转效应。本文延续基于风险的理论分析视角,以2005—2021年中国A股市场的股票作为研究对象,研究波动持续性对股票预期回报和反转效应的影响。首先,本文采用GARCH项系数的绝对值作为个股在考察期内波动持续性的度量。本文通过投资组合分析法在时间序列层面考察股价波动持续性与股票预期收益之间的关系,研究发现波动持续性与股票预期收益之间存在显著的负相关关系;通过构建多空组合,买入波动持续性小的股票同时卖出波动持续性大的股票能获得显著的超额收益。混同横截面回归分析证明,股价波动持续性与股票未来收益在横截面上依然存在显著的负相关关系。在以上研究的基础上,本文进一步探索股价波动持续性对股票未来收益的影响呈现出动量特征还是反转特征。本文针对全样本验证了A股市场主要存在反转效应。根据股价波动持续性的大小将样本分为5组,在每一组中执行反转策略,研究发现,随着股价波动持续性的增大,反转收益变大,说明波动持续性大的股票组合相对于波动持续性小的股票组合更容易发生反转。经过CAPM模型和三因子模型风险调整后,结果依然稳健,即股价波动持续性放大了反转收益。
本文的研究结论对了解中国资本市场规律、健全资本市场和提高市场有效性都具有一定的意义。基于上述研究结论,本文提出以下建议:投资和资产管理部门在建立投资组合时,应纳入刻画股价波动持续性和反转效应的因子,并根据因子关键变量的变化调整投资组合,改善投资业绩;监管部门在风险预警时也应加强对股价波动持续性变量的重视和实时关注,未雨绸缪,预防系统性金融风险的扩大和蔓延,促进资本市场健康发展。
注 释:
①即收益率序列在一段时间内表现出持续的高波动性或者持续的低波动性。
②根据Wind的数据,截至2021年12月31日,按照流通市值计算的我国A股市场散户投资者占比为97.24%。
③根据Choice 的数据,2011—2020年上证指数10年间的换手率为1 193.16%。
④鉴于后文验证得到中国A股市场存在“反转效应”的特征事实,可以在不同波动持续性组内构建多空组合,买入过去表现较差的股票,卖出过去表现较好的股票,即在每个组内执行反转策略,观察不同组反转策略的收益。如果随着波动持续性增大,反转策略的收益率逐渐增大,即说明波动持续性能够放大反转效应。
⑤限于篇幅,具体实证结果未列示,留存备索。作者邮箱:rzhang@ustb.edu.cn.

