基于粒子群优化的模糊自适应等效油耗最小能量管理策略

潘公宇,郭丛揺,晋恩荣

(江苏大学 汽车与交通工程学院, 江苏 镇江 212013)

0 引言

近年来,交通拥堵、能源危机、环境污染等问题日益严重[1]。在此背景下,零排放成为汽车行业的发展方向,但受制于充电设施建设和电池技术等因素的限制,目前混合动力汽车依然是实用性较高的节能与新能源汽车产品[2]。目前混合动力汽车能量管理策略通常分为基于规则的能量管理策略、全局优化能量管理策略和瞬时优化能量管理策略等。常见的基于规则的能量管理策略包括确定性规则[3-4]和模糊规则[5],基于全局优化的控制策略利用最优化方法求解最小化成本函数控制动作序列[6-7]。瞬时优化能量管理策略不同于全局优化能量管理策略需要提前预知驾驶信息,对未知驾驶信息的依赖程度有所降低,有着较好的实际应用前景[8]。在瞬时优化策略中较为典型的控制策略为等效燃油消耗最小(ECMS)策略,该策略由Paganelli等[9]提出,目的在于降低混合动力系统的燃油消耗。ECMS策略的基本原理为通过引入等效因子将电能转化为等效的燃油消耗,然后建立系统瞬时燃油消耗代价函数,在控制变量的可行范围内求解最佳控制变量,使得瞬时等效油耗最小。与基于规则的能量管理策略相比,ECMS策略通过引入等效因子可以实现能量分配的非线性求解,因此相较于基于规则的控制策略有着更好的控制效果[10]。但ECMS策略对于等效油耗的计算方式严重依赖于等效因子取值,并且在现有研究中大多基于标准工况进行等效因子的标定,因此如何根据随机的驾驶条件获得准确的等效因子,提高等效因子在不同工况下的适应性也成为当前研究的主要目标。

近年来大量学者对于混合动力汽车应用等效燃油消耗最小策略中的等效因子的调节提出了不同的改进方案,目前有关等效因子自适应调节方法主要分为基于电池SOC反馈方法[11]、离线优化和在线识别相结合[12],以及根据预测信息对等效因子进行调节的方法[13]。其中基于电池SOC反馈的A-ECMS策略虽然不需要依赖未来的行驶信息,但其控制效果很大程度上取决于自适应控制中的相关系数设置的合理性,因此仅基于SOC平衡的等效因子反馈调节存在一定的局限性[14]。在车辆的实际行驶过程中,不同工况类型、每一时刻的需求功率和实际SOC都对等效因子的调节有一定的影响,而基于SOC反馈修正等效因子属于一种事后补偿方法,单纯依靠SOC反馈调节具有一定的局限性,若能综合考虑实际SOC与参考SOC之间的差值,以及需求功率等因素对等效因子的影响,并对等效因子的修正方法进行调节则可获得更好的控制效果。

其中对等效因子的修正方法进行调节的重点在于对比例系数的调节,即需要根据不同因素之间的关系选取合适的比例系数,但是不同因素对比例系数的影响较为复杂,难以利用数学公式对其进行准确描述。因此针对比例系数与实际SOC、参考SOC和需求功率之间的复杂非显式关系,可以考虑通过模糊逻辑的思想确定比例系数,本文在基于SOC反馈的等效因子比例控制调节机制中引入模糊控制作为调节比例系数的手段,并利用权重线性递减的PSO算法对模糊控制隶属度函数进行优化,进一步解决模糊控制在汽车能量管理应用中过于依赖专家经验的问题。

1 混合动力系统建模

1.1 动力系统结构与参数

本文以某款混合动力城市公交客车为研究对象,其动力系统结构如图1所示,主要部件参数如表1所示,其中动力系统主要由发动机、电机MG1、电机MG2、电池组以及前行星排PG1、后行星排PG2等相关部件构成,前排行星齿轮机构为输入式功率分流装置,后排行星齿轮机构的齿圈固连接在机壳上,其发动机输出轴连接前行星排的行星架,电机MG1连接PG1的太阳轮,电机MG2连接PG2的太阳轮,PG1的齿圈和PG2的行星架相连,进一步根据各动力源与行星齿轮的连接关系,可以得到系统输出转速、转矩的关系,如式(1)所示。

图1 混合动力系统构型

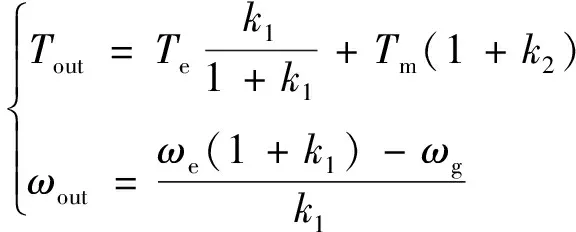
(1)

式中：Tout为系统输出轴转矩;Te为发动机转矩;Tm为电机MG2转矩;k1和k2分别为前行星排和后行星排的特征参数;ωout为系统输出轴转速;ωe为发动机转速;ωg为电机MG1转速。

1.2 发动机模型

发动机模型的建立采用实验建模法利用插值法和发动机特性试验数据,构建映射输入输出的查表模型,主要包括转矩计算模块、燃油消耗模块,当已知发动机转速nen和转矩Ten后,实际燃油消耗的计算公式为：

(2)

式中：Fuel为实际燃油消耗量;mf(nen,Ten)为燃油消耗率,整个行驶工况的实际燃油消耗量为每一时刻燃油消耗率关于时间的积分。

1.3 电机模型

混合动力结构涉及2个电机,都可以工作在电动模式或发电模式,由于电机理论建模复杂利用数学模型对其行为描述较为困难,因此本文采用试验建模,建立效率与转速转矩相关的准未带查表模型,其中模型的输出转矩表达式为：

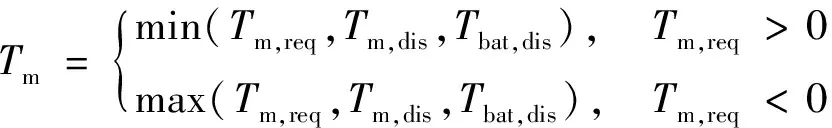
(3)

式中：Tm,req为电机需求转矩;Tm,dis为电机驱动状态下的最大输出转矩,由电机的最大功率和电机的转速决定;Tbat,dis为电池组功率所允许的最大驱动转矩,由电池组的最大功率和电机的转速决定。

1.4 电池模型

电池模型采用内阻模型对电池建模,SOC计算模块通过剩余容量和总容量的比值表示电池SOC,表示为

(4)

(5)

式中：Qmax、Qused分别为电池最大容量和使用容量;SOC0为初始SOC;Ibat为电池电流;电池输出电压Ubat可表示为

Ubat=Uoc-IbatRoc

(6)

式中,Uoc、Roc分别为电池包的开路电压和内阻,可根据温度与SOC查表得到。

2 自适应ECMS策略

2.1 ECMS控制策略

等效油耗最小能量管理策略(equivalent consumption minimization stratery,ECMS)属于一种基于瞬时优化的能量管理策略,一方面通过建立消耗电能与用于补偿消耗电能所需的燃油之间换算关系,实现对电池电量的维持,然后将实际发动机消耗的燃油与补偿电能消耗的燃油进行叠加,并将叠加后的瞬时总等效燃油消耗作为能耗指标进行优化控制,即为ECMS策略中有关等效油耗的核心概念。另一方面对于瞬时优化的实现方式为ECMS策略在每个控制步长内,在满足整车需求功率的情况下,将瞬时总等效燃油消耗最小作为控制目标,对发动机和电机的分配方式进行优化。

ECMS的优点是无须预知完整工况并且计算速度快,因此可以实现在线应用。由于电池初始和最终SOC的差异较小,相当于实际消耗的能量都来自于燃油,而电池也就相当于缓冲装置,所以ECMS本质在于充放电过程所产生的电量的消耗都可以折算成燃油消耗量。其原理如图2所示,在电池放电情况下,电池消耗的电能由未来时刻发动机消耗的燃油进行补充;在电池充电情况下,所补充的电能也会在未来时刻消耗,相当于节约了未来的燃油消耗。

优化控制量可通过求解最小瞬时等效油耗获得,瞬时等效油耗为实际油耗与电能折算后的等效油耗之和：

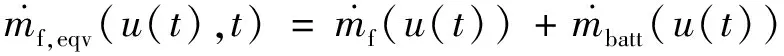
(7)

将电能折算为等效油耗如下所示：

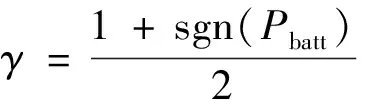
(9)

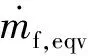
以电池SOC作为状态变量,发动机转矩转速作为控制变量,系统的约束条件为：

(10)

式中：SOCmin、SOCmax分别表示SOC最小值与最大值;Pbatt,min、Pbatt,max分别表示电池功率最小值与最大值;Teng,min、ωeng,min、Teng,max、ωeng,max分别表示发动机转矩转速最小值与最大值;Tmot,min、ωmot,min、Tmot,max、ωmot,max分别表示电机转矩转速最小值与最大值;Tgen,min、ωgen,min、Tgen,max、ωgen,max分别表示发电机转矩转速最小值与最大值。

ECMS的计算流程可描述为：

1) 确定ECMS中等效因子的取值,根据实际行驶过程中每一时刻的需求转矩,以及混合动力系统中各动力源与双行星齿轮机构的输出转速与转矩的数学关系,将发动机电机划分为一定数量的满足驱动需求的转矩组合;

2) 根据发动机电机等部件的操作限制,筛选剔除不在约束范围内的转矩转速组合;

3) 根据不同的转矩转速组合利用发动机燃油消耗MAP图和电机等效燃油计算公式对该分配方式下总的等效油耗进行计算,通过求解目标函数最小值获得最小的等效燃油消耗量和对应的发动机电机的分配方式;

4) 将当前时刻满足约束的对应最小燃油消耗量的最优解输出到各个部件模块中。

具体ECMS计算流程如图3所示。

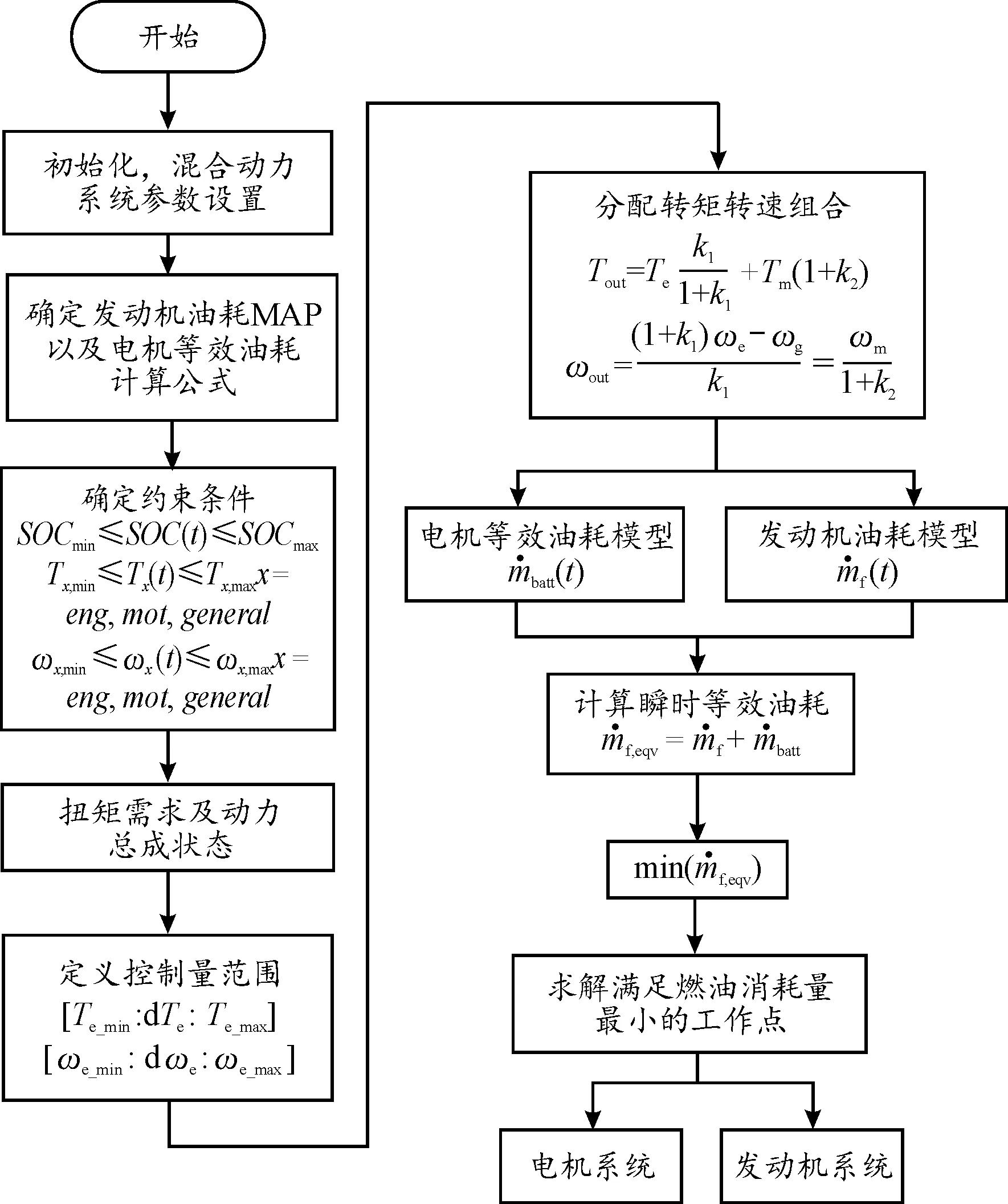
图3 ECMS算法流程图

2.2 A-ECMS控制策略

针对2.1节的分析可以得到在等效油耗最小能量管理策略中,等效因子对于求解最优控制序列起到了至关重要的作用,但是恒定等效因子在车辆实际行驶过程中对工况适应性较差不能针对工况的变化实时调整,可能会出现用电成本偏高或偏低的情况从而造成电池电量的维持效果不佳,因此为了进一步提高等效油耗最小策略在实际工况中的应用效果,可采用自适应的等效因子调节方法提高其工况适应性。

根据对等效因子的分析可知等效因子的取值对能量管理策略的影响较大,当等效因子取值偏大时,可能会造成策略减少电量消耗从而使SOC有增加的趋势;当等效因子取值偏小时,可能会造成策略增加电量消耗从而使SOC有减少的趋势。基于比例控制的等效因子修正方法主要原理为：根据实际SOC与参考SOC之间的差值,以及上一时刻的等效因子对实际行驶过程中的等效因子进行自适应反馈,具体表达式为：

sk=sk-1+Kp(SOCref-SOC(t))

(11)

式中：sk为第k次调节后的等效因子;Kp为比例系数;SOCref为参考SOC。基于比例控制的等效因子在每个固定时间内根据实际SOC与参考SOC之间的差值实时调整等效因子的取值,若实际SOC取值小于参考SOC,则下一时间间隔的等效因子便会增加;若实际SOC大于参考SOC,则下一时间间隔的等效因子便会减小。

具体等效因子自适应调节规律如图4(a)所示。当k时刻时,实际等效因子低于最优等效因子,导致电池具有放电趋势,如果不进行自适应调整,在下一时间段内电池SOC会进一步降低,可能会导致电池过放电的现象出现,若采用自适应调节方法则等效因子会有增大趋势,随着等效因子的增大使得电池能够减少放电具有充电趋势;与之相反如图4(b)所示,当k时刻时,实际等效因子高于最优等效因子,导致电池具有充电趋势,如果不进行自适应调整,在下一时间段内电池SOC会进一步升高,可能会导致电池过充电的现象出现,若采用自适应调节方法则等效因子会有减小趋势,随着等效因子的减小使得电池能够减少充电具有放电趋势。

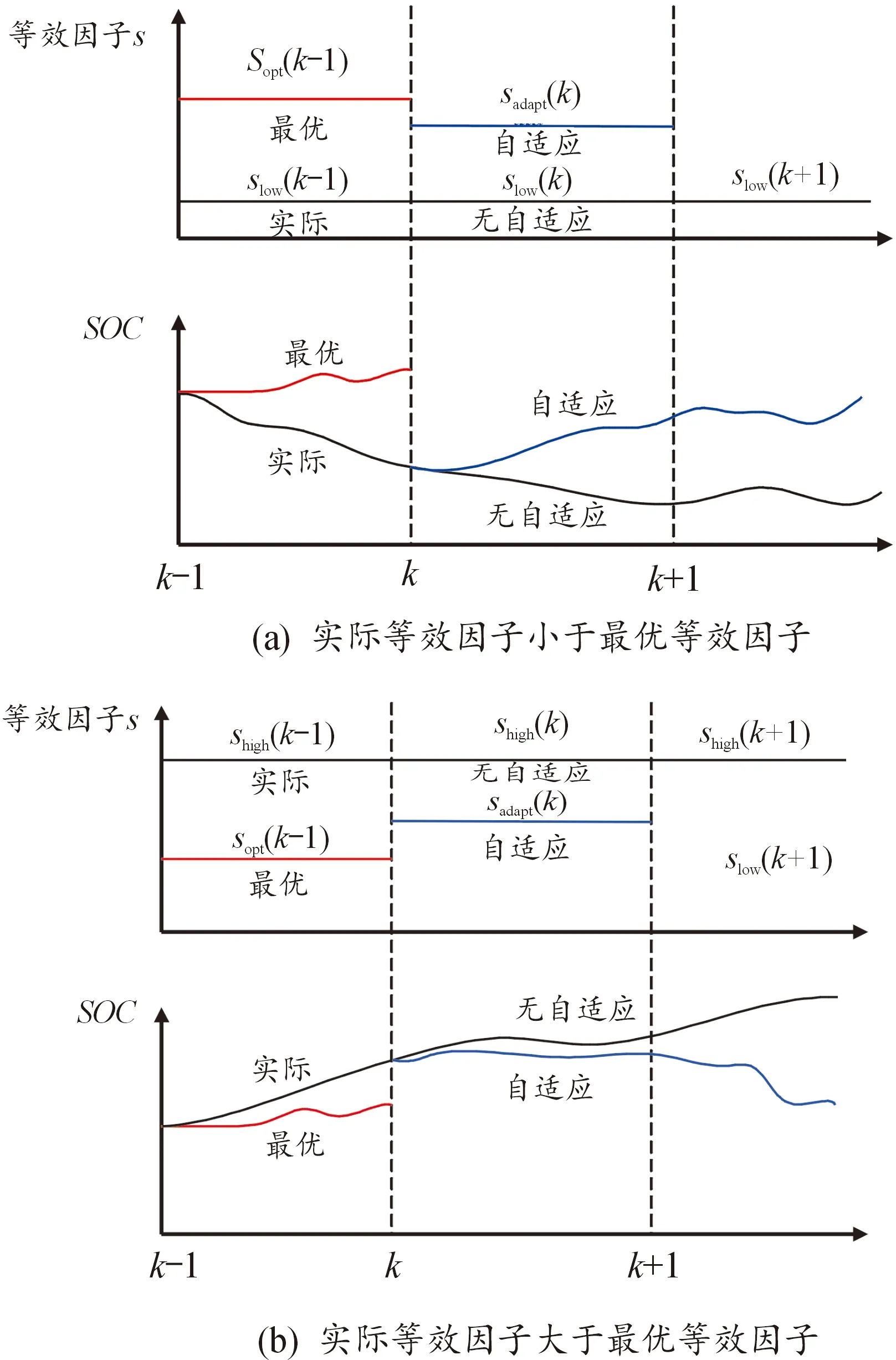
图4 等效因子自适应调节规律

3 基于粒子群优化的模糊A-ECMS策略

3.1 模糊A-ECMS策略

根据对自适应等效油耗最小策略的分析可以得出,采用基于比例控制的等效因子修正方法与恒定等效因子相比能够更好地维持电池电量的平衡,但在车辆实际行驶过程中,不同工况类型、每一时刻的需求功率和实际SOC都对等效因子的调节有一定的影响,而基于SOC反馈修正等效因子属于一种事后补偿方法,单纯依靠SOC反馈调节具有一定的局限性,若能综合考虑实际SOC与参考SOC之间的差值,以及需求功率等因素对等效因子的影响,并对等效因子的修正方法进行调节则可获得更好的控制效果。对式(11)进行分析可以发现,对等效因子的修正方法进行调节的重点在于对比例系数的调节,即需要根据不同因素之间的关系选取合适的比例系数,但是不同因素对比例系数的影响较为复杂,难以利用数学公式对其进行准确描述。因此针对比例系数与实际SOC、参考SOC和需求功率之间的复杂非显式关系,可以考虑通过模糊逻辑的思想确定比例系数,本文在基于SOC反馈的等效因子比例控制调节机制中引入模糊控制作为调节比例系数的手段。

模糊控制是一种以模糊集合论、模糊语言变量和模糊逻辑推理为基础的控制方法,其以工程经验为规则建立输入与输出之间的映射关系。模糊控制器的具体结构如图5所示,主要包括模糊化、知识库、模糊推理和解模糊4部分。

图5 模糊控制器结构示意图

3.1.1模糊控制器变量的确定

通过对等效燃油消耗最小能量管理策略的分析可知,能量管理的目标是对燃油消耗量和电量消耗量进行合理分配并维持SOC平衡,由于本文主要采用基于比例控制的等效因子修正方法,因此将比例系数作为模糊控制器的输出。同时整车需求功率、实际SOC与参考SOC之间的差值对能量源的分配与SOC的稳定影响较大,因而选取实际SOC与参考SOC的差值和整车需求功率作为模糊控制器的输入,故本节设计的模糊控制器为两输入单输出的形式。

3.1.2隶属度函数的确定

隶属度函数能够表示论域中的元素与隶属度之间的关系,在对模糊控制器中的隶属度函数设计时,需要确定模糊子集的个数和隶属度函数的范围形状,本文利用高斯型隶属度函数响应迅速计算简单的特点对函数形状进行定义。对于实际SOC与参考SOC的差值,其论域设置为[-0.1,0.1],划分为7个模糊子集{负大,负中,负小,零,正小,正中,正大},分别用{NB,NM,NS,O,PS,PM,PB}表示。整车需求功率设置为[-250,250],并划分为7个模糊子集。输出变量为比例系数,论域设置为[1,15],模糊子集同样划分为7个模糊子集。图6为输入输出变量的隶属度函数。

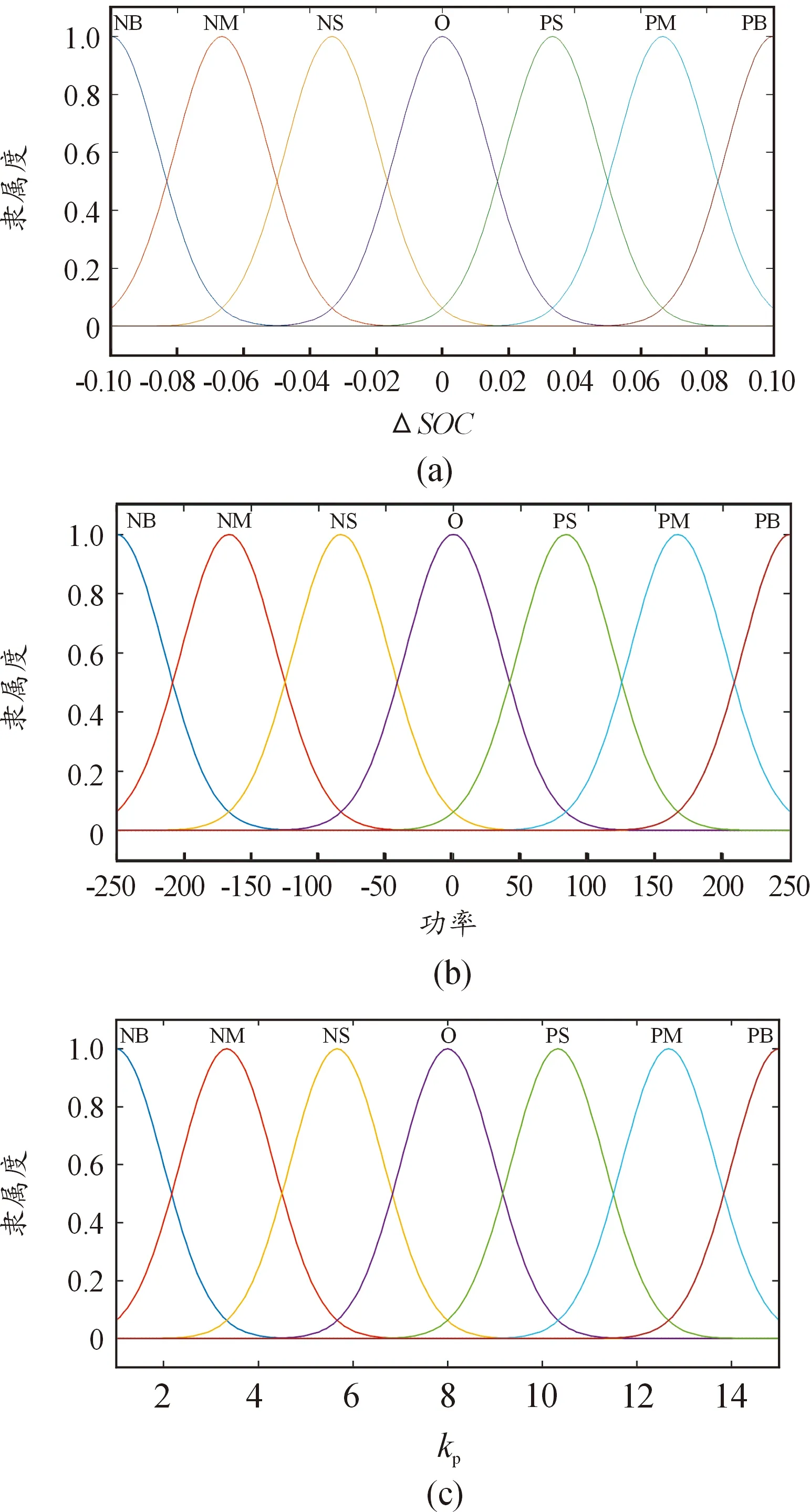
图6 输入输出变量隶属度函数

3.1.3模糊规则的确定

模糊规则制定采用if ΔSOCisAand power isB,thenkpisC的形式,在制定模糊规则时需要考虑以下条件,当ΔSOC为较大负值时,说明动力电池SOC高于SOCref较多,若此时需求功率为较大负值,则应调节比例系数为较大值,从而使等效因子取较小值,减小电能消耗的成本,使其具有放电趋势,实现维持SOC平衡的目的;当ΔSOC为较小负值或较小正值时,说明动力电池SOC偏离SOCref较小,若需求功率为较大负值或较小正值时,则应调节比例系数为较小值,从而使等效因子在小幅度进行调节;当ΔSOC为较大正值时,说明动力电池SOC低于SOCref较多,若需求功率为较大负值或较小正值,则可相应减小比例系数的取值,使其等效因子相对有所增加,减少放电趋势,若此时需求功率为正值且较大,则应调节比例系数为较大值,从而使等效因子取较大值,增加电能消耗的成本使其具有充电趋势。根据以上分析,建立模糊控制规则如表2所示,模糊推理曲面如图7所示。

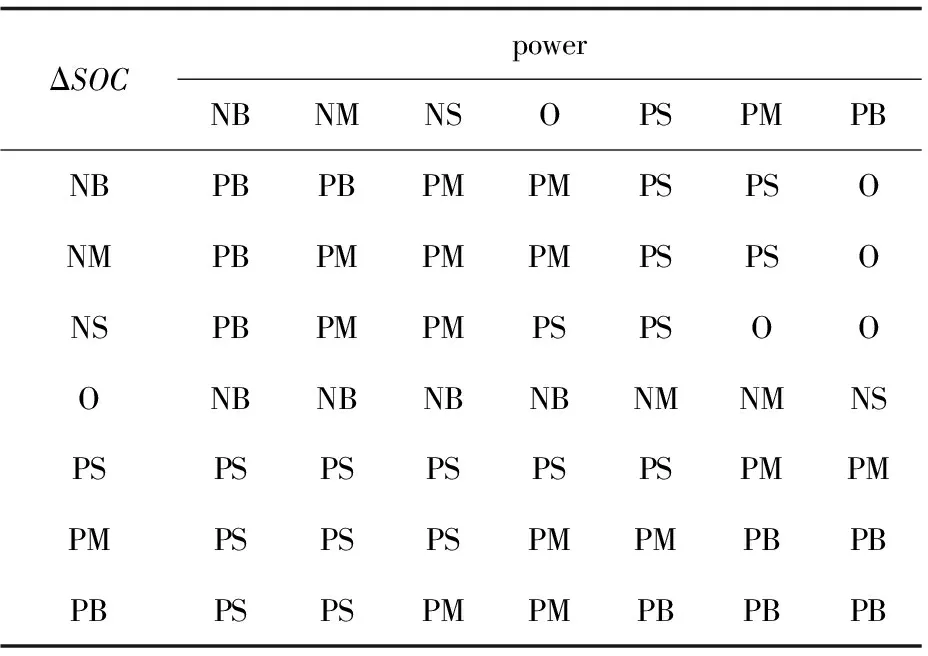
表2 模糊控制规则

图7 模糊推理曲面

3.2 带惯性权重线性递减的PSO算法

由于在设计模糊控制器的过程中,隶属度函数主要通过专家知识和工程经验来确定,因此容易受主观因素影响使其控制参数并不是最优值。考虑到粒子群优化算法具有参数设置简单、易于实现、优化能力强、收敛速度快等特点,因此本节引入粒子群优化算法,在中国公交典型工况下以燃油消耗量,以及电池SOC与参考值的差值最小为优化目标,求解出隶属度函数最优控制参数,建立基于粒子群优化的模糊A-ECMS策略。

粒子群优化算法是由Kennedy和Eberhart提出的一种基于群体的随机优化算法。PSO在求解最优解的过程中模仿鸟类的觅食行为,将问题的搜索空间比作鸟类的飞行空间,其中每只鸟都可抽象为一个微粒用以表示问题的一个候选解。例如,d维目标搜索空间内的第i个粒子的位置用Xi=(Xi1,Xi2,…,Xid)表示,速度用Vi=(Vi1,Vi2,…,Vid)表示,在每一次迭代过程中评价目标函数,确定t时刻每个粒子所经过的最佳位置与群体的最佳位置,其中粒子个体i经历过的最佳位置用pbesti=(pi1,pi2,…,pid)表示,种群经历过的最佳位置用gbest=(g1,g2,…,gd)表示,每个粒子位置和速度的更新方式如式(12)：

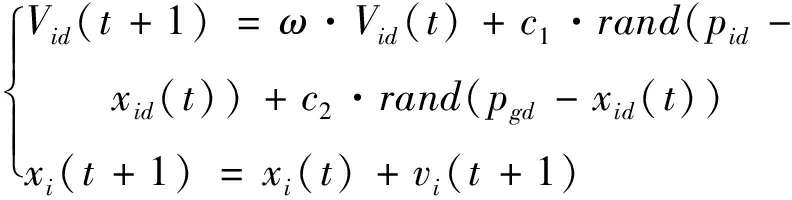
(12)

式中：c1为学习因子;rand为随机函数;ω为惯性权重因子。

算法性能依赖于参数的设置,微粒群的个数、惯性权重ω、学习因子等参数设置的不同也会导致结果有所差异。其中惯性权重ω主要影响微粒的局部最优能力和全局最优能力,当ω取较大值时有利于提高算法的全局搜索能力,当ω取值较小时有利于提高算法的局部搜索能力。综合考虑较大的权重因子有利于跳出局部最优解便于全局搜索,较小的权重因子有利于局部搜索便于算法收敛,因此本文采用线性变化的权重因子,使得惯性权重因子从最大值ωmax线性减小到ωmin,其中惯性权重因子随算法迭代次数变化的公式为：

(13)

式中：ωmax和ωmin分别为ω的最大值和最小值;t为当前迭代次数;tmax为最大迭代步数。

3.3 基于粒子群优化的模糊A-ECMS策略

本文将实际SOC与参考SOC的差值,以及整车需求功率作为模糊控制器的输入,利用粒子群优化算法对用于调节比例系数的模糊控制器中的隶属度函数的控制参数进行离线优化,将优化后的结果在线应用在实际的控制系统中,完整控制策略如图8所示。

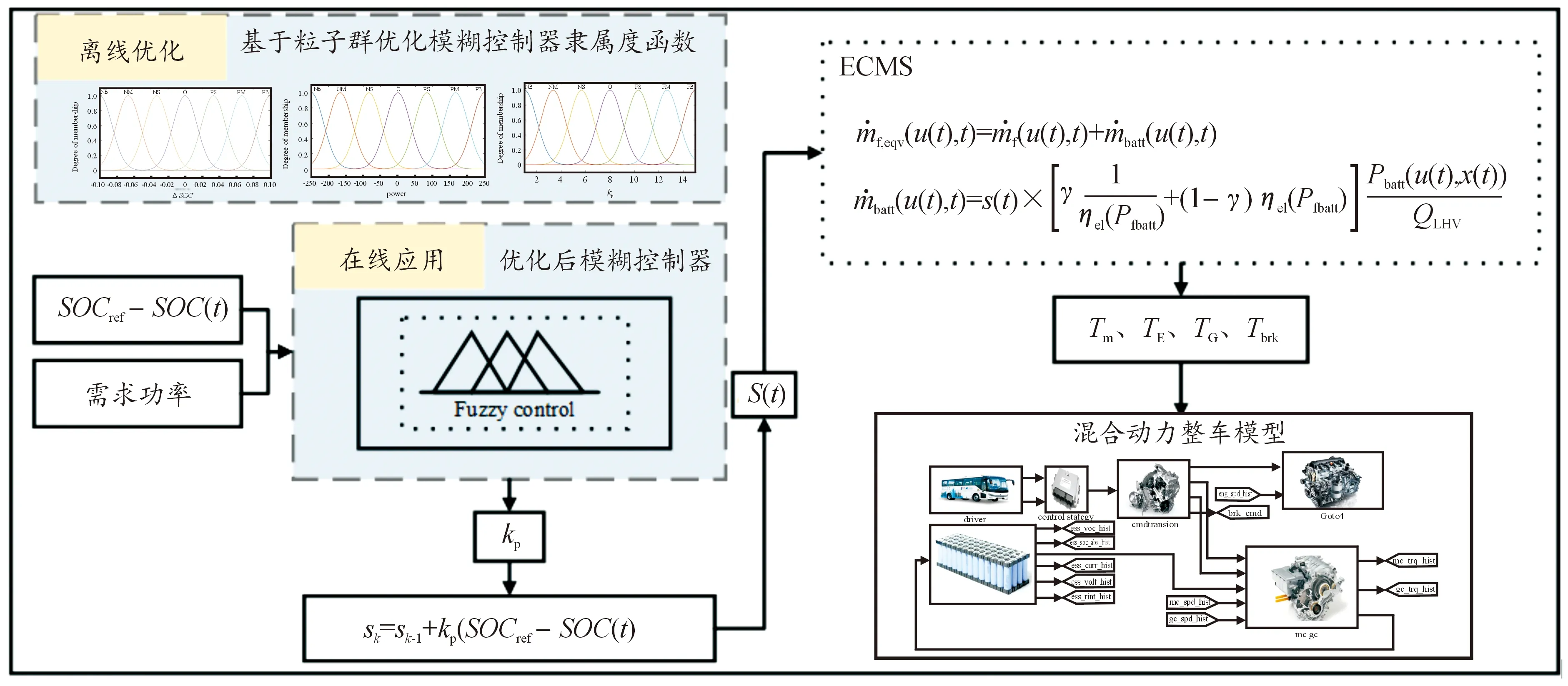
图8 基于粒子群优化的模糊A-ECMS策略

在3.1小节设计的模糊控制器的输入输出变量隶属度函数均采用了均匀划分的方式,但根据实际问题进行综合分析后对隶属度函数进行划分可获得更好的控制效果,因此本节以减小燃油消耗量以及电池SOC与参考值的偏差为目标建立相应的适应度函数,具体表达式为：

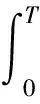
(14)

式中：mfuel为燃油消耗量;γ为与SOC相关的惩罚系数,其中γ=1×105;SOCend为SOC的最终取值;SOCref为SOC的参考值,SOCref=0.55。

另外,本文设计的模糊控制器选取高斯型函数作为隶属度函数,为gaussmf(X,PARAMS),表示在X处计算高斯函数,其中PARAMS为二元向量用于决定隶属度函数的形状和位置,具体表达式为：

gaussmf(X,(σ,C))=exp(-(X-C)2/(2*σ2))

(15)

在Matlab/Simulink中模糊控制控制工具箱中,高斯型隶属度函数控制参数主要为σ与C。其中,取值对隶属度函数的影响如图9所示,图中分别取当σ=0.5、σ=1、σ=2、σ=3以及C=2、C=4、C=6、C=8对应的情况。

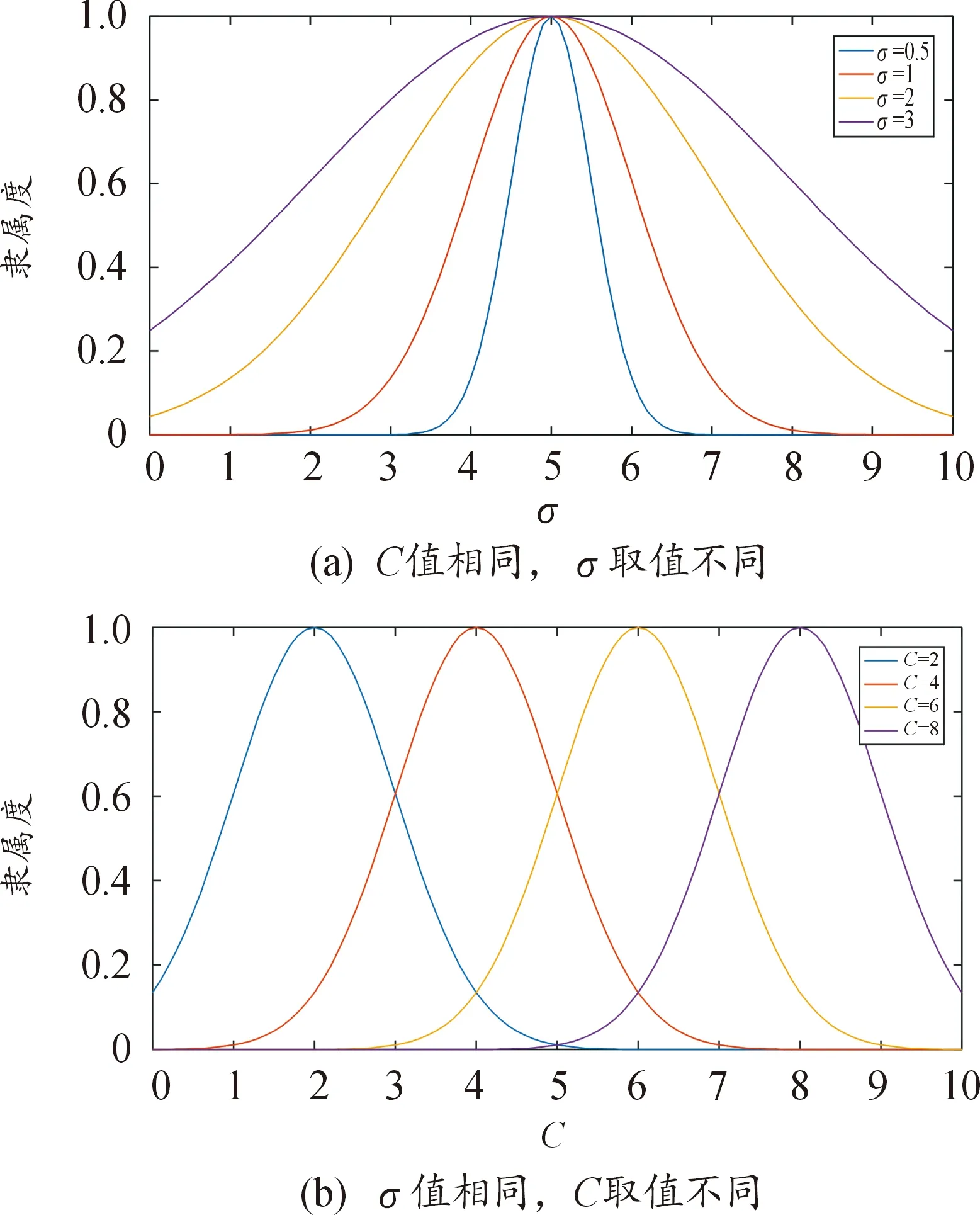
图9 不同σ与C取值对应图像

由于高斯型隶属度函数的形状和位置主要取决于σ与C,因此本文针对σ与C两参数进行优化求解,其坐标分别为a1、a2、a3、b1、b2、b3、c1、c2、c3,具体隶属度函数优化参数如表3所示。

粒子群算法步骤主要为：

1) 初始化种群中各微粒的位置和速度,将各微粒的历史最优位置pbest设为初始位置,取种群最优位置为gbest中的最优值;

2) 计算各微粒的适应度值,并存储每个微粒的最佳位置与适应度值;

3) 根据式(12)更新微粒的速度和位置;

4) 计算每个微粒更新位置后的适应度值,并与之前最佳位置对应的适应度值进行比较,若优于之前的适应度值则将当前位置作为该粒子的pbest;

5) 将每个微粒的适应度与种群微粒的最佳位置gbest进行比较,如果较好,则更新gbest的值;

6) 判断是否满足终止条件,即达到最大迭代次数或达到最优适应度值,若不满足则在此进入循环,若满足则停止迭代,输出最优解。

算法流程如图10所示。

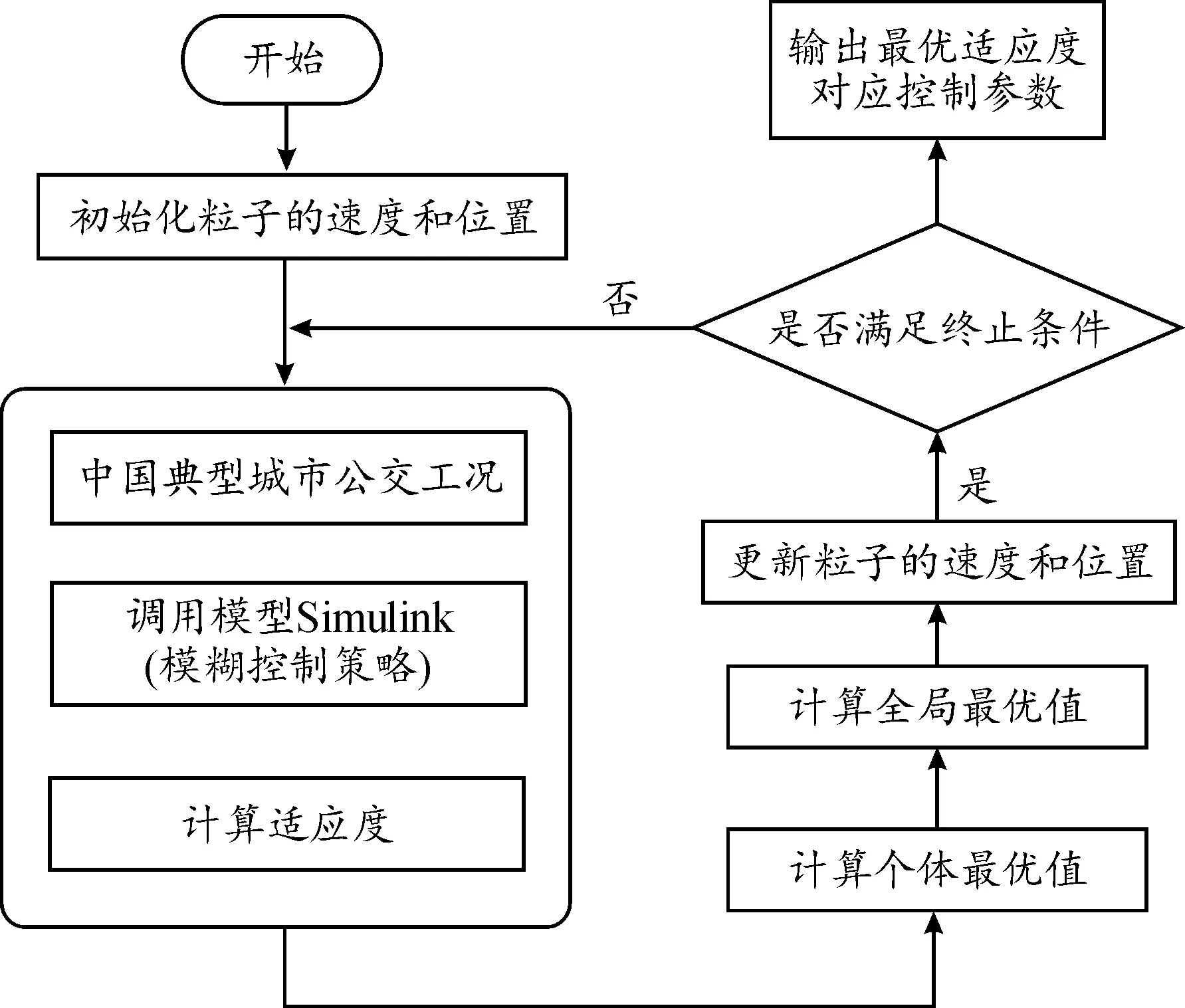
图10 粒子群算法优化流程

3.4 仿真及结果分析

本文设置得最大惯性权重因子ωmax为1,最小惯性权重因子为0.6,c1与c2取值为2,维度为9,其中种群数量如果太小会降低种群多样性,如果种群数量太大会增加计算量影响优化效率,因此本文选择种群规模为30,最大迭代次数为10。其中优化后的隶属度函数如图11所示,优化前后各参数如表4所示。

表4 优化前后各参数值

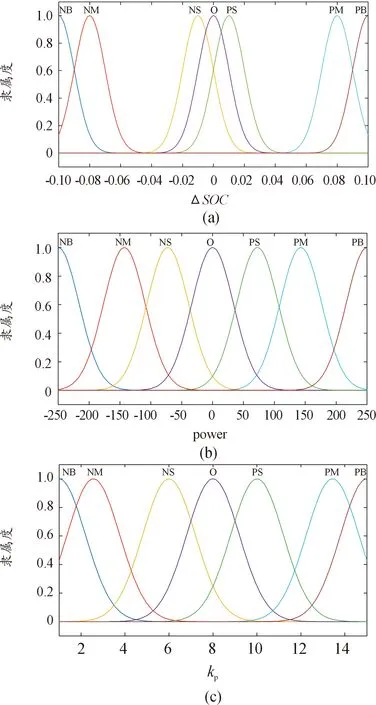
图11 优化后的隶属度函数

通过对结果的分析可知,利用带权重线性递减的PSO算法优化求解得到的最优高斯型隶属度函数控制参数与基于专家经验设计的模糊控制器的隶属度函数在形状和位置上都有一定区别,其中优化过程中的适应度曲线如图12。

图13—17给出了中国典型城市公交工况(CCBC)下基于本文提出的PSO-fuzzy A-ECMS策略和基于SOC反馈调节的A-ECMS控制策略的仿真结果,包括发动机电机转矩变化、电池SOC、发动机油耗、发动机工作点MAP图,其中循环工况如图18所示,仿真采用整车模型如图19所示。由图13—14优化前后发动机和电机的转矩变化曲线可以看出,2种策略均可以将不同动力源的输出量限制在合理范围内,满足整车的控制要求。

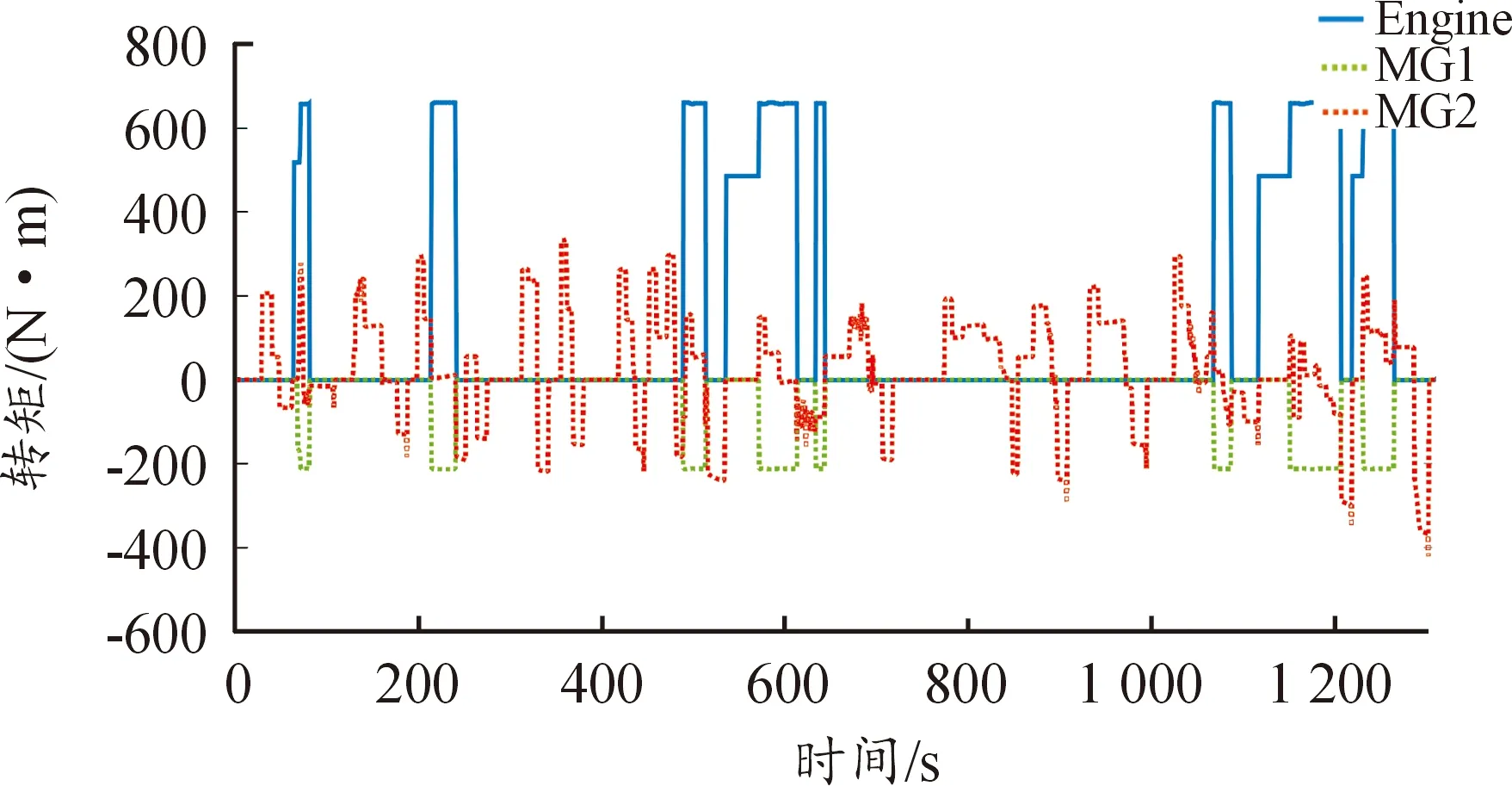
图13 A-ECMS策略发动机、电机转矩变化曲线

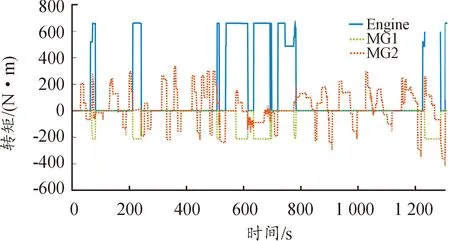
图14 PSO-fuzzy A-ECMS策略发动机电机转矩变化曲线

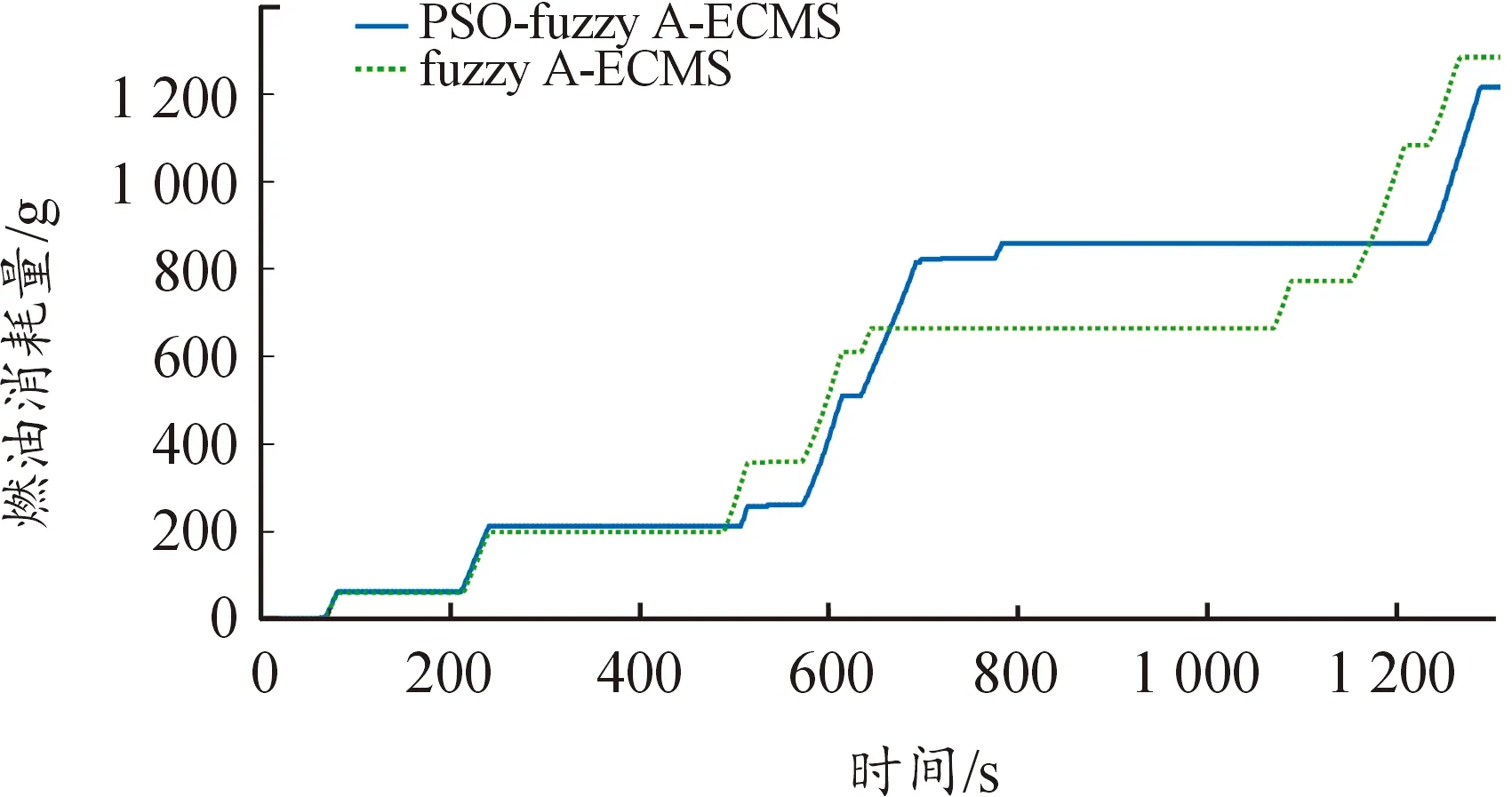
图16 燃油消耗量变化曲线

图17 发动机工作点MAP图

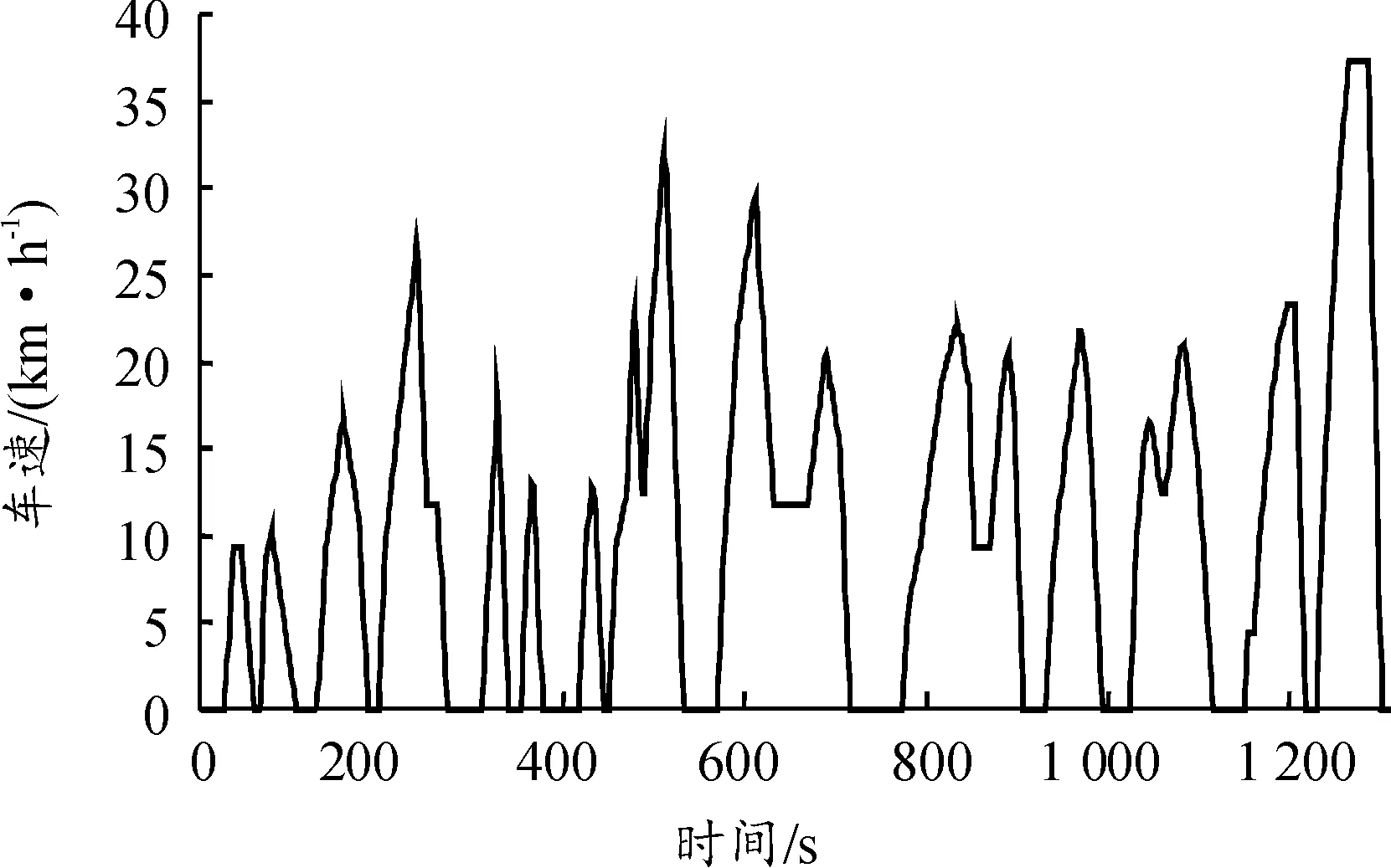
图18 中国典型城市公交工况

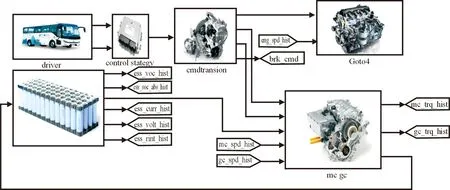
图19 混合动力汽车整车模型

优化前后的燃油消耗量和SOC曲线如图15—16所示。由图15可知,在初始值为0.55的前提下,基于SOC反馈的自适应等效油耗最小能量管理策略(A-ECMS)与利用带权重线性递减PSO算法优化的模糊自适应的等效燃油消耗最小能量管理策略(PSO-fuzzy A-ECMS)均能够保证SOC在合理范围内波动,但两者最终SOC的取值有一定的差异,在1 800～1 300 s的工况区间内,相较于本文提出的策略,未经过优化的A-ECMS策略对于电能消耗的评估权重过高,即由电能等效的燃油消耗更“昂贵”,导致燃油消耗量过多,电能持续增加,因此A-ECMS策略在行程结束时最终SOC高于SOCref,电池充电明显,因而发动机的燃油消耗量也较高。而经过带权重线性递减PSO算法优化的模糊A-ECMS策略在行程结束时SOC值与SOCref偏差较小,能够更好地维持电池的充放电平衡。由图17可知,常规A-ECMS策略发动机工作点大部分在高效运行区间外,发动机输出效率低,本文提出的PSO-fuzzy A-ECMS能够使发动机更多地工作在高效区间内,从而进一步提高整车的燃油经济性。

4 结论

在基于SOC反馈原理对等效因子进行比例调节方法的基础上,提出一种基于粒子群算法优化的模糊自适应等效燃油消耗最小的能量管理策略,定性分析了A-ECMS策略中不同因素对等效因子修正的影响。相较于基于SOC反馈的A-ECMS策略仿真结果表明,本文设计策略能够减少模糊控制在能量管理应用中对专家经验的依赖,在CCBC工况下使整车燃油经济性提高5.33%,同时能够维持SOC在合理区间内变化,终值SOC接近于初始SOC,在电池SOC出现过充过放前能够快速做出反应维持SOC平衡,证明所制定的策略具有一定的有效性和可行性。