基于特斯拉阀的新型非接触式流体密封技术研究
王 衍 ,谢雪非 ,何一鸣 ,黄周鑫 ,徐 慧 ,柴代泽 ,杨怀石
(1.江苏海洋大学 机械工程学院,江苏 连云港 222005;2.江苏省海洋资源开发研究院,江苏 连云港 222005)
现代工业水平迅速发展导致的生产装置大型化与高度集成化,凸显出生产装备长周期安全运行的重要性.对装备长周期安全运行、环境保护和资源节约的要求,使得流体密封技术一直是国内外学者和工程技术人员关注的焦点和研究热点[1-2].
根据工作原理的不同,流体密封可分为流体静密封和动密封两大类.前者是指2个相对静止零件接合面间的密封,后者是指2个相对运动零件接合面间的密封.流体动密封是工业装备中主要使用的密封形式,按工作时密封端面间是否存在承载流体,流体动密封主要分为接触式(机械密封、填料密封和唇形密封等),非接触式(间隙密封、迷宫密封、气膜密封、离心密封和螺旋密封等)及其他形式(刷式密封、磁流体密封和指尖密封等)[3-4].其中,非接触式流体密封不存在固相直接接触,磨损小、寿命长,主要依赖节流效应或动压效应实现密封,已作为先进密封技术用于压缩机、汽轮机和航空发动机等高端装备[5].但是此类密封是靠动力元件产生动压效应工作的,对主轴转速有较大依赖,当速度较低或停车时,密封能力消失,往往需要辅以停车密封,进而使得整个密封结构变得复杂.密封装置的工作性质及装配位置,决定了失效后的维修工作非常繁琐.据统计,在日常的机器设备使用和维修中,密封部分几乎占到设备维修总量的40%~50%[6],离心泵的维修费大约有70%用于处理密封故障,严重的密封失效甚至会引起易燃、易爆及有害介质大量泄漏而酿成事故[7].因此,在满足密封要求的同时,如何提高密封的使用寿命及结构稳定性,降低维修周期及简化密封系统,对于密封技术的实际应用具有重要意义.
面对传统接触式流体密封功耗大、高工况场合适应性差以及非接触式流体密封辅助系统复杂、维护成本高等问题,启发于特斯拉阀的被动式流体控制原理及单向导通特性,本文中提出将这种结构从平面流动扩展至三维管状通道流动,将单向导通升级用于单向(高压侧至低压侧)泄漏抑制.旨在通过对密封通道的宏观重构,揭示被动式流体阻塞机制,突破传统流体密封无法兼顾非接触和简约性结构的矛盾束缚,为进一步简化密封结构,实现零磨损、低泄漏的新型密封开辟新方向.
1 技术背景
1.1 典型密封结构
机械密封作为接触式流体密封的典型代表,也是工业用动密封的主要型式,广泛应用于电力、船舶和石油化工等领域,其典型结构如图1所示.可以看出,机械密封主要依靠动静环紧密贴合来阻塞介质的泄漏,辅助动静环的还有弹簧、弹簧座、紧定螺钉、密封圈和防转销等零件.
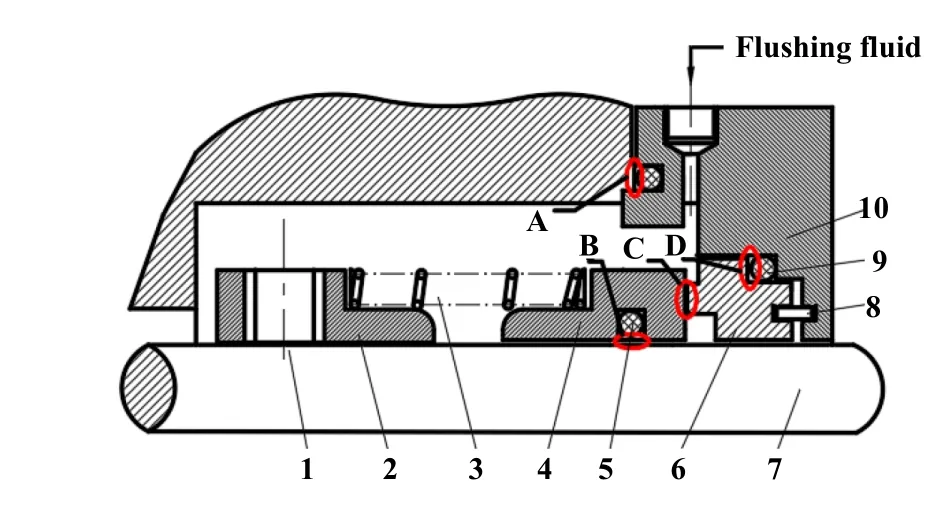
Fig.1 Schematic diagram of mechanical seal structure图1 机械密封结构示意图
非接触式机械密封的典型结构与图1中相似,不同之处主要在于密封环端面是否开有动压槽.在动环或静环上开槽都可以,一般选择开在两环中较耐磨的环上,且多沿环的外径侧开槽,沿内径侧开槽多用于泵送类密封.除了包含以上基本构件外,非接触式机械密封还包括停车密封、供气/液系统以及气液过滤/回收系统等辅助系统,结构更加复杂.
1.2 特斯拉阀结构及工作原理
特斯拉阀是由科学家尼古拉·特斯拉提出且以自己名字命名的1种单向导通阀,于1920年申请了发明专利[8].该阀体结构无任何活动部件,仅利用空间结构推动流体流动,无需输入能量即可实现流体的单向导通[9-10].如图2所示,流体正向流动与反向流动差别巨大,正向流动时,流体能够绕过所有翼状障碍畅通无阻地从右边流至左边,并且因流动压力可获得加速效果;但当流体反向流动时,每经过1个通道,就要向上/下进入1个翼状障碍,在弯管与水平管道交汇处形成剧烈的冲击阻塞效应,使得内部能量、流速和压力等被消耗.翼状障碍越多,流体向前推进的阻力越大,造就了特斯拉阀独特的单向导通效果.特斯拉本人给出1个概念:假设流体经过第1个翼状障碍后的泄漏用分数1/X表示,在经过第n个翼状障碍后,泄漏仅为(1/X)n,很明显,X不需要很大的数字,即可确保1个近乎完美的阀门节流行为.

Fig.2 Schematic diagram of the Tesla valve图2 特斯拉阀原理图
虽然特斯拉阀提出时间较早,在微尺度上有许多优点,但是,关于其研究的文献较少,这一巧妙结构真正得到重视和应用仅在最近几年.2003年,Truong等[11]提出了1种综合优化方法,首次实现了特斯拉阀结构参数的完整设计和系统优化.2005年,Gamboa等[12]进一步采用6个独立设计变量对特斯拉阀进行了几何优化,使得流阻力比提高25%,得到了单向导通效率最高的GMF型特斯拉阀.2011年,Thompson等[13]尝试将特斯拉阀结构用于平板振荡热管(FP -OHP)的止回阀设计,该设计可以有效促进所需循环流量,较传统止回阀始终具有更低的热阻(降阻约15%~25%).接着,Thompson等[14]又对多级特斯拉止回阀进行了三维数值研究,结果表明,多级结构具有更高的单向导通效率,且随雷诺数的增大,效率提升更加显著.2014年,Wang等[15]将特斯拉阀结构用于微型混合器并进行了数值模拟,结果表明,特斯拉阀混合器在低雷诺数下具有更低的压降和更高的混合性能,更加适用于现代生物医学芯片和化学反应器中.2017年,Vries等[16]在特斯拉阀结构的基础,成功设计了1种新型脉动热管(PHP)阀,显著促进了管内流体循环并使热阻效率有效降低14%.2018年,Porwal等[17]采用计算流体力学(CFD,Computational fluid dynamics)方法数值分析了进口雷诺数对单级和多级特斯拉阀整流和热增强能力的影响,结果表明,采用特斯拉阀门作为小型或微型热交换器、热敏二极管或止回阀时,可以有效提升热/流量控制效率.2018年开始,浙江大学钱锦远等[18-20]对特斯拉阀进行了系统研究,结果表明特斯拉阀在离子流动尺度仍然适用,并将该结构成功用于氢燃料电池的氢减压过程,提出的多级反流状态特斯拉阀门具有良好的减压效果.2020年,Abdelwahed等[21]采用拓扑梯度数值优化算法对二维特斯拉微阀进行了重构,该算法可以有效提高特斯拉阀流域摄动函数的灵敏度.同年,Wahidi等[22]将改进的特斯拉阀用于超临界CO2自然循环回路中,结果表明,改进的特斯拉阀可以更好地稳定超临界压力和热输入,而且在不降低传热性能的情况下,还可以缓解温度和速度振荡.
以上研究表明,特斯拉阀这一巧妙结构已日益引起各领域学者的关注和浓厚兴趣,在诸多设备上的应用也都具有显著效果.根据这一结构反向流动时的逐级节流特性,理论上可建立起阻塞密封功能.
1.3 新型密封结构及工作原理
特斯拉阀的被动式流体控制原理及其内部流体产生的冲击阻塞形式,导致这一阀型的单向导通特性,依据这一特点,尝试将这种结构从平面流动扩展至三维管状通道形式的新型密封结构,如图3所示,该结构部件组成十分简洁,除了转动轴及其连接部分外,不含有其他额外活动部件,主要包括1-外环、2-悬柱、3-键、4-内环和5-轴.内环通过键等直接置于轴套或轴上并随之旋转,外环可以直接依托密封端盖或壳体固联不动,悬柱可通过内置螺钉和双头螺柱等形式分别固定于内环或外环上.
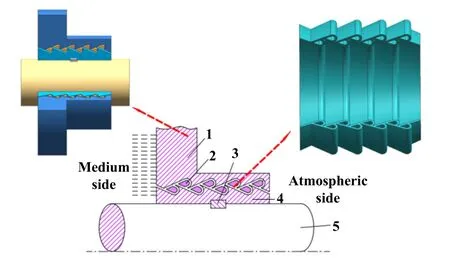
Fig.3 Three-dimensional tubular new sealing structure diagram图3 三维管状新型密封结构图
类似于平面特斯拉阀的翼状通道,规定1个悬柱与对应的内外环部分组成的空间为1个密封级,出、入口端分别为大气侧及密封介质高压侧,之间三维特斯拉阀状通道为反向布置,高压介质通过入口进入后会被逐级阻流、降压,理论上当级数足够多,压降至与大气压一致时,即可实现密封结构的单向泄漏抑制.
2 计算模型
2.1 物理模型
图3所示的结构存在明显弊端,其内外环及悬柱等三大件集成和安装存在干涉问题,鉴于此,提出改进结构,如图4(a)所示,该结构密封级间为阶梯状连接,由装配关系决定悬柱置于内环或外环上(外环部位悬柱需为剖分式),可以实现轴向装配.轴向截面尺寸如图4(b)所示,每个密封级尺寸相同,左侧为入口,右侧为出口.密封级结构主要由回转半径R、标准流距L及分流角α等参数决定,回转半径可以决定内置悬柱的尺寸,标准流距主要影响密封级数的整体布置紧凑度,通过调整分流角可以实现密封级径向和轴向布置效率的改变,密封级R、L和α三者存在互相制约的关系.h为密封间距,根据内外环及悬柱尺寸及固定位置可形成既定间隙.
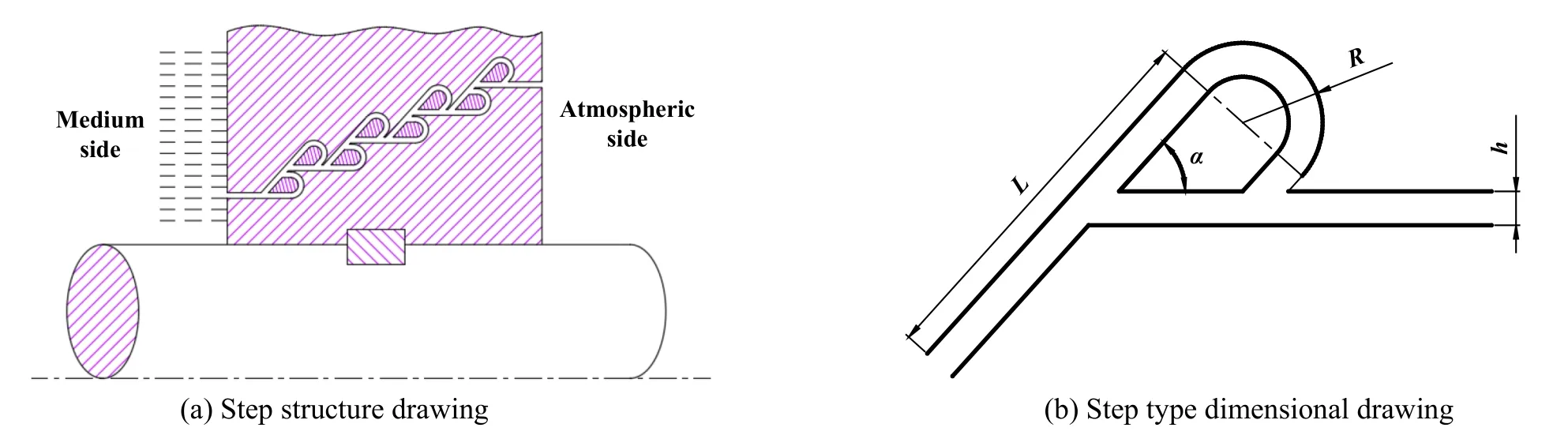
Fig.4 Step-type new sealing physical model图4 阶梯型新型密封物理模型
此外,实际装配过程中还应考虑部件间的定位和精度保证,以确保新型密封对结构精度的要求.后续实际使用时为避免介质结焦、结垢和结晶等对流道的填塞,还应确保介质的洁净和流道的畅通等问题.
2.2 基本参数
新型密封基本参数列于表1中,对部分参数的区间范围作了限定,需要在相对不变量的前提下进行系统研究.右侧设定的相对不变量,为研究某一具体参数变化规律时其他参数的具体取值.
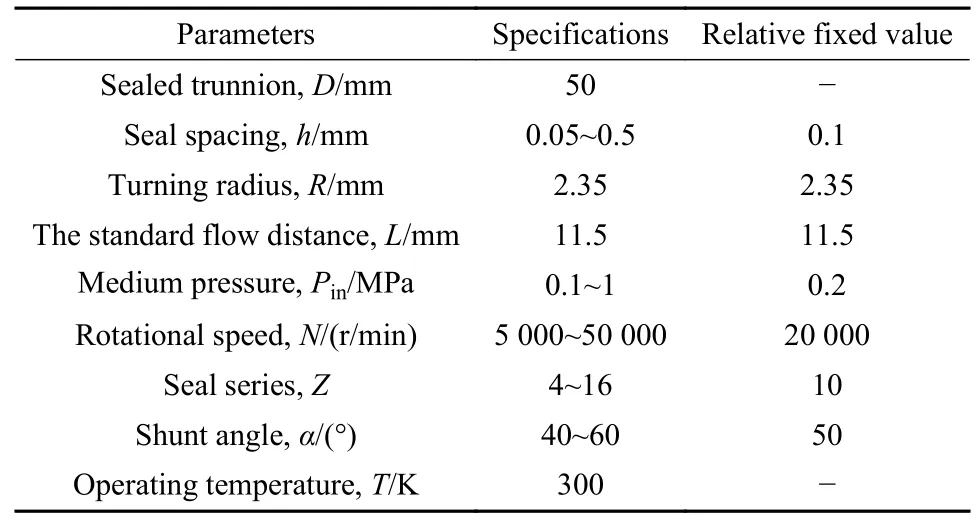
表1 新型密封几何参数Table 1 Geometric parameters of the new sealing
2.3 流动损失
2.3.1 压头损失
密封的泄漏由压差造成,压差(ΔP)与系统的压头损失密切相关.根据流体力学基本原理[23],新型密封的压头损失主要包括沿程损失hf和局部损失hj:
其中,ρ为介质密度;g为重力加速度.
根据特斯拉阀单项导通特性,新型密封的局部损失要远大于沿程损失,沿程损失主要指各级间沿标准流距L处的损失,根据沿程损失计算方法[24],可表示如下:
其中,λ为沿程阻力系数,由雷诺数确定;De为当量直径,对于同心缝隙取De=2h;v为平均流速,分别对应路径取值.
图5所示为单节密封截面示意图,由图5可以看出,局部损失由弯管和三通损失构成.流动路径包括L1和L2这2条支路,局部损失需分路径具体分析,流经L1的流体,局部损失由1处弯管结构C1和2处三通结构T1及T2产生;流经L2的流体,局部损失由2处三通结构T1和T2产生,如式(3)所示.
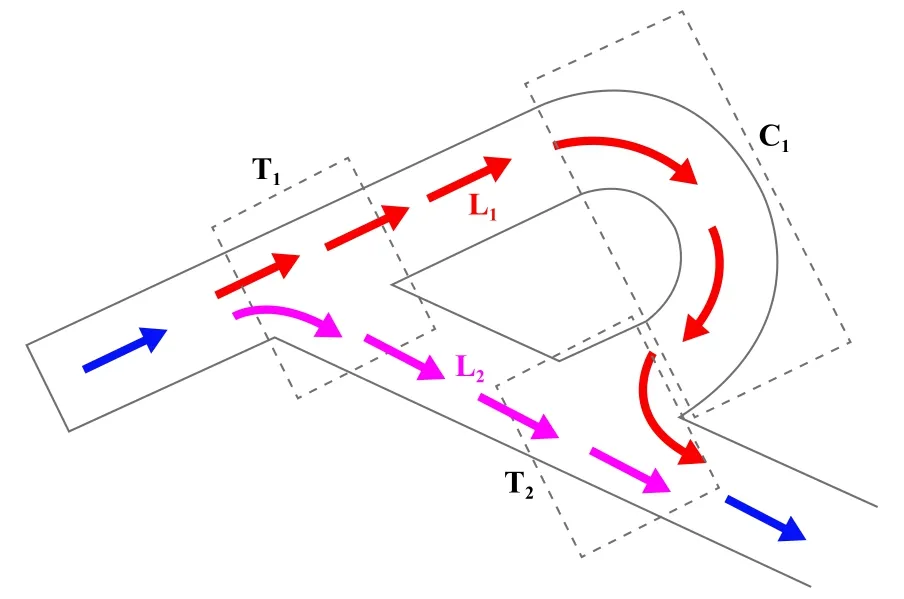
Fig.5 Flow diagram图5 流动示意图
其中,ζ为各路径局部阻力系数,下标L1、L2、C1、T1和T2分别代表对应值.可以看出,单节密封级的局部阻力系数Kj为路径L1和L2上的并联和,单节阻力系数为局部阻力系数Kj和沿程阻力系数λ的串联和.由于沿程阻力系数λ是随雷诺数的变量,对整个密封的综合阻力系数K计算表达式如下:
各路径局部阻力系数可参考流体力学中各类三通结构进行取值,并列于表2中.鉴于新型密封的级数Z多是成对增加的,表2计算并列出了各偶数密封级数对应的局部阻力系数.
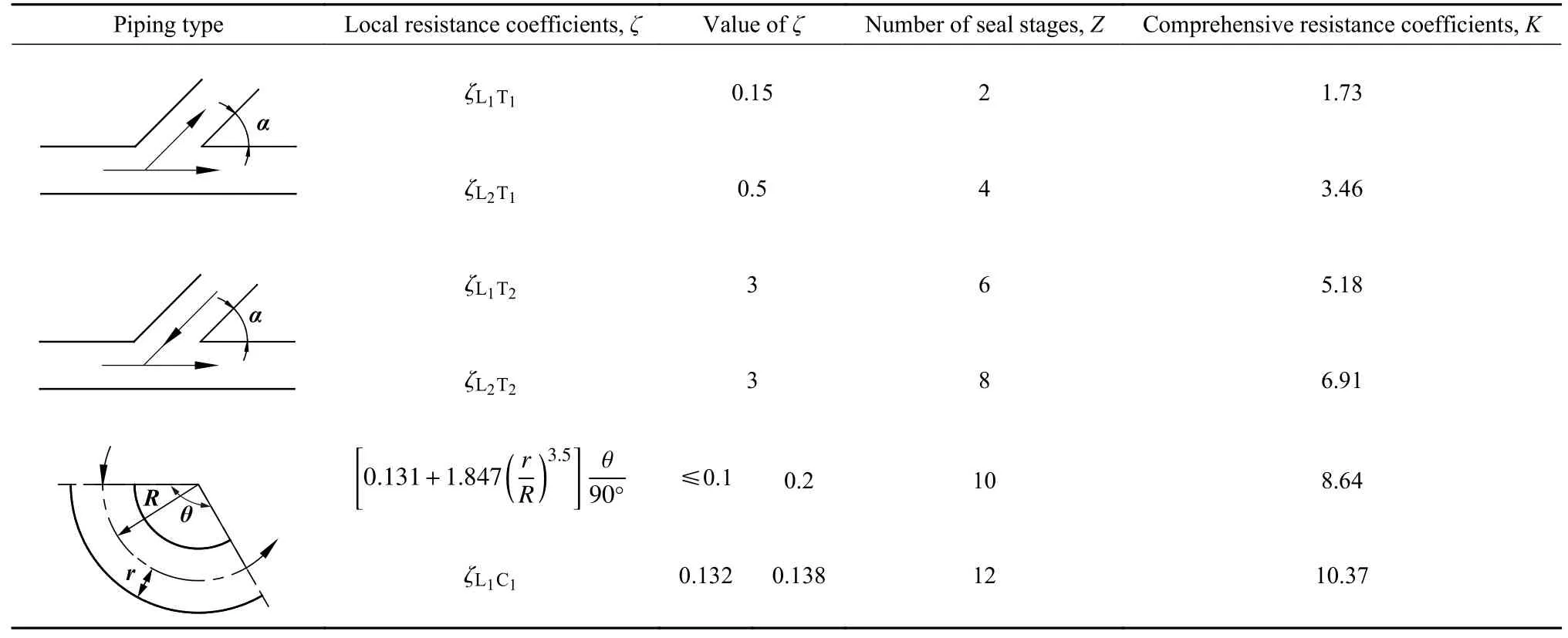
表2 不同路径及密封级对应局部阻力系数[25]Table 2 Different paths and sealing stages correspond to local resistance coefficients
2.3.2 泄漏损失
新型密封流场类似于间隙密封,实际为同心环形缝隙流动的1种,可视作平板流动的延伸[26].如图6所示,由于新型密封包含旋转流场,以vx表示沿x向切向速度,vy表示轴向速度,Bi、l和h分别对应新型密封周向、轴向和径向尺寸.通过简化Navier-Stokes方程并在z向2次积分,可得速度矢量.运用速度分解定律,即可得出轴向速度微分形式,积分后所得表达式如下:
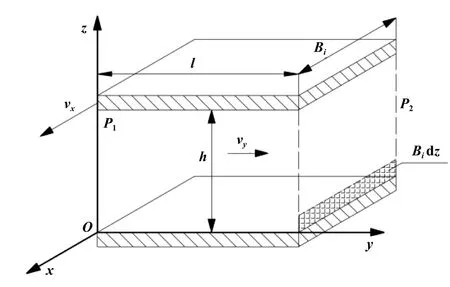
Fig.6 Schematic diagram of plate flow图6 平板流动示意图
其中,μ为流体动力黏度;h为密封间距.
以任意节(假设Z=i)特斯拉阀为研究对象,取微元面积Bidz,如图6所示.沿z=0至h积分,可得到单节泄漏率,求和所有密封级,即可建立整体泄漏率(Qo)表达式如下:
其中,Qi为第i级出口泄漏率;Bi为第i级的水平出口外壁截面周长;vxi为第i级沿x向切向速度;ΔPi为第i级压头损失.
Groddeck[27]通过Yamada[28]的试验结果表明,层流时壁面旋转几乎不会影响流体介质的通流过程,甚至不影响可压缩介质的通流过程.当流体为湍流时,Groddeck进一步给出了考虑旋转剪切的泄漏计算公式:
其中,vx和vy取做流动管道的平均值.令Q=0,可分别解出:
(1) 无泄漏间距越大,说明在较大间距下即可实现理想密封效果,越容易实现密封,密封能力相对越强,反之亦然;
(2) 无泄漏压差越大,表明可在较高压力下实现理想密封效果,密封能力相对越强,反之亦然.
2.4 三维管状泄漏通道模型
建立如图7所示三维阶梯型新型密封流道模型,依据装配关系,左边为介质高压入口侧,右边为大气低压侧.为准确获得新型密封的各项性能指标,选择全尺寸建模,降低局部建模对仿真计算结果的影响.
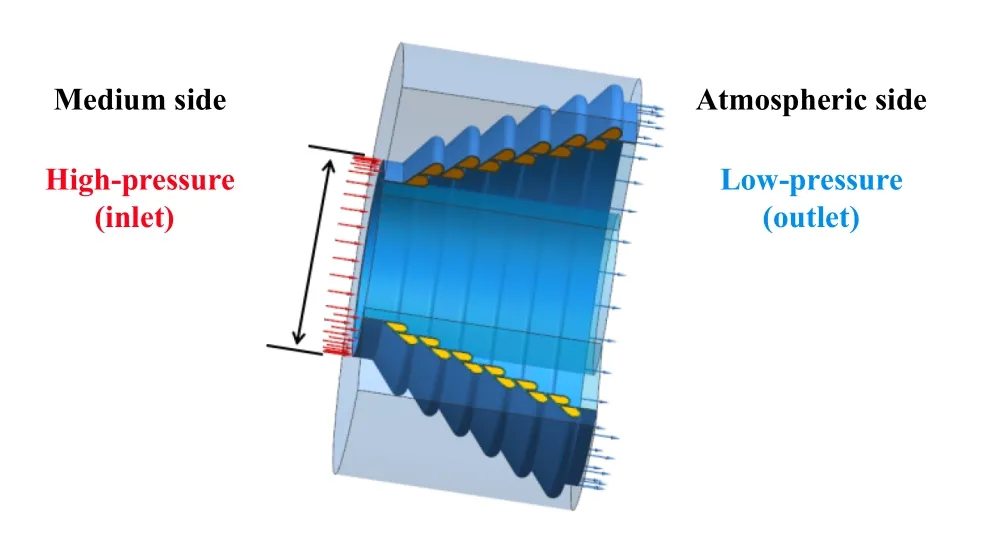
Fig.7 Step-type new sealing flow channel model图7 阶梯型新型密封流道模型
3 仿真模拟
3.1 基本假设
鉴于特斯拉阀结构适宜低黏度流体[29],密封介质选择空气,研究新型密封工作机制还需要对不同工况和不同几何参数下的密封性能作系统研究.为便于解决问题,对新型密封流道模型作如下假设:
(1) 三维管状通道间的流体为连续介质流动[30];
(2) 流场中的气体为常温和常黏度介质[31];
(3) 流场内润滑层管道壁面紧密吸附,无滑移产生;
(4) 忽略密封通道变形对流体流动的影响;
(5) 不计气体惯性力的影响;
(6) 运行过程中管道间隙不变,管道表面理论光滑.
3.2 控制方程及求解
本文中采用ANSYS开发的Fluent软件对三维管状新型密封进行数值模拟,该结构为三维管流算例.定常不可压缩流体的控制方程可表示为如下通用形式:
其中,ρ为流体密度,φ为求解变量,u,v和w分别为轴向、径向和切向流体流动速度,Γφ为扩散系数,Sφ为源项.
边界条件采用强制性压力边界条件,入口处:p=Pin(介质压力);出口处:p=Po(大气压).新型密封流体行为是典型的内部及强曲率分离流动,属于湍流流场.本文中选用Fluent软件中的湍流模型(动能-耗散率,k-ω)进行求解,其优势在于计算该类流场时不会忽略近壁处缓冲区的流动,可以较精确地计算逆压梯度和强曲率流场[32].采用SIMPLE算法进行亚松弛迭代计算,通过中心差分对扩散项离散,对流项计算采用二阶迎风格式,连续方程和动量方程的迭代精度设为10-5,能量方程的迭代精度设为10-6.
3.3 网格划分
采用UG软件对新型密封进行全尺寸建模,然后导入Fluent meshing进行网格划分,可以通过对Surface Mesh Controls系列参数(Min size,Max size,Growth及Cells per gap等)的整体控制和调整,实现模型的网格划分及局部加密,网格效果如图8(a)所示.以泄漏率为指标进行网格无关性验证,如图8(b)所示,当网格数达到700万以后计算结果基本趋于稳定,以此为基准进行网格划分可以兼顾计算效率和精度的要求.
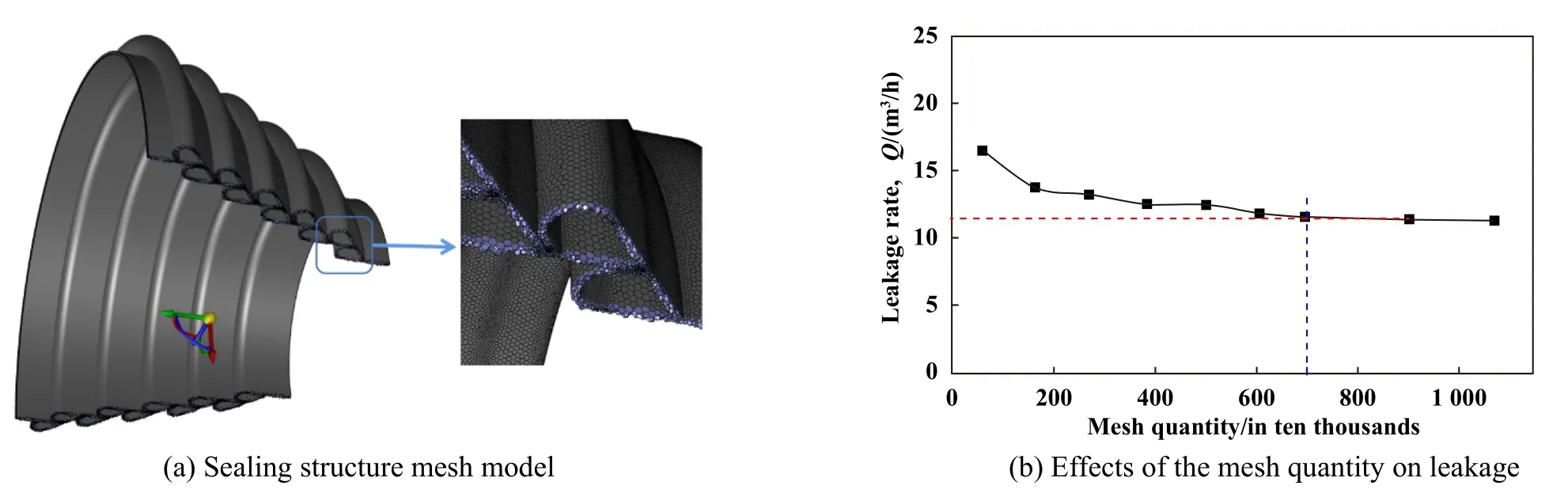
Fig.8 Mesh generation图8 网格划分
4 计算结果与分析
4.1 流场特性
图9(a)和图9(b)所示分别为不同级数位置对应的压力云图和速度云图,并对流体流动的交汇区进行了局部放大.可以看出,在交汇区都可以观察到明显的压力和速度波动,局部流动由于流体间的冲撞和分叉流等变得不稳定.气体由高压端入口进入后,压力和流速都呈逐级降低的趋势,表明气体进入后通过逐级节流,压差可能造成的速度升高也逐渐被节流效果抵消和抑制.此外,在汇集夹角处还产生了二次流现象,这些都造成了能量的损失,进而使压力和速度降低,有利于密封功能的实现.
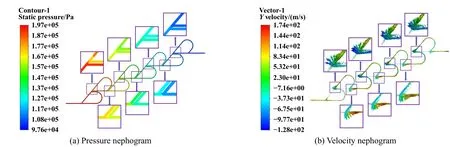
Fig.9 Flow field characteristics(h=0.3 mm,Pin=0.2 MPa,N=20000 r/min,Z=8,T=300 K)图9 流场特性(h=0.3 mm,Pin=0.2 MPa,N=20000 r/min,Z=8,T=300 K)
4.2 流体性质对密封性能的影响
4.2.1 介质密度
图10所示为介质密度对密封性能的影响规律,可以看出,介质密度对无泄漏间距和无泄漏压力基本没有影响,泄漏率随介质密度的增大呈缓慢降低趋势,表明新型密封较适于高密度介质.综合而言,新型密封对介质密度属性敏感度较低,对较高密度介质的适应性稍好.
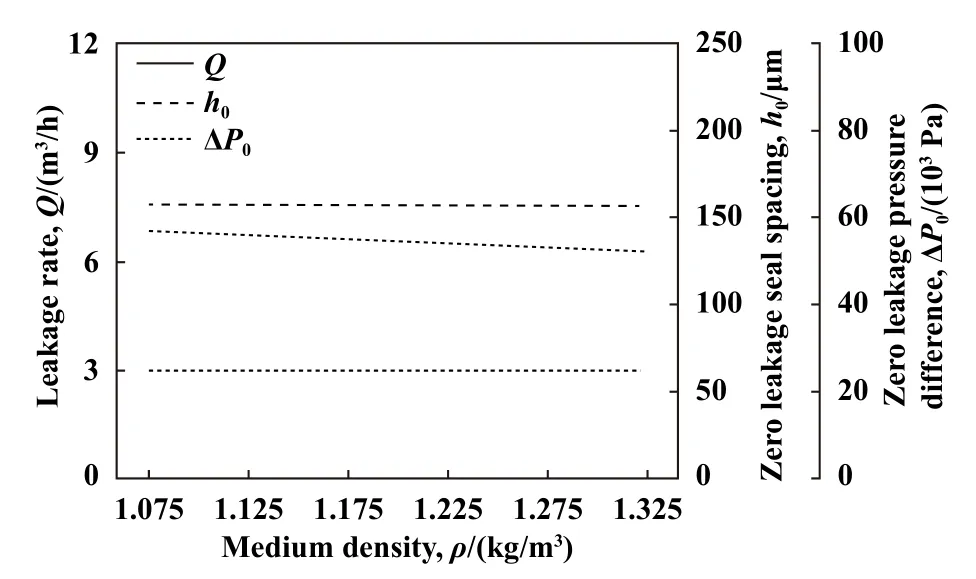
Fig.10 Effects of medium density on sealing performance图10 介质密度对密封性能的影响(h=0.1 mm,Pin=0.2 MPa,N=20000 r/min,Z=10,T=300 K)
4.2.2 介质黏度
如图11所示,与介质密度的影响特点不同,介质黏度对密封性能有显著影响.泄漏率随介质黏度的增大呈显著降低趋势,而无泄漏间距和无泄漏压力则随介质黏度的增大而增大.泄漏率随介质黏度的变化可直接说明新型密封适于高黏度介质流动,再参考无泄漏间距和无泄漏压力可知:较高的介质黏度一方面可以降低新型密封的泄漏率,同时也能在一定程度上提高无泄漏间距和无泄漏压力,进而提高密封综合性能.综上可见,新型密封对高黏度介质下的流体流动密封效果最好,也最容易实现.
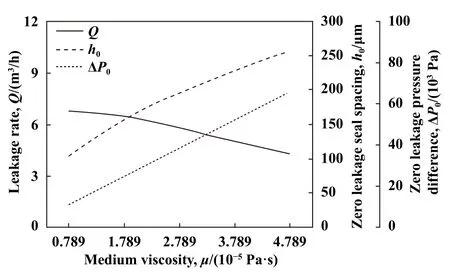
Fig.11 Effects of medium viscosity on sealing performance图11 介质黏度对密封性能的影响(h=0.1 mm,Pin=0.2 MPa,N=20000 r/min,Z=10,T=300 K)
4.3 工况参数对密封性能的影响
4.3.1 介质压力
如图12所示,介质压力对密封性能参数影响较大,随着介质压力的升高,泄漏率和无泄漏间距分别呈显著增大和降低趋势,无泄漏压力根据模型的定义与压力变化无关.无泄漏间距随介质压力的升高呈降低趋势,这一现象说明:其他工况条件不变的情况下,压力越高,新型密封泄漏率越大,理论上需要更小的密封间隙才能实现新型密封的抑漏功能,侧面也说明了通过减小密封间隙可以降低泄漏.
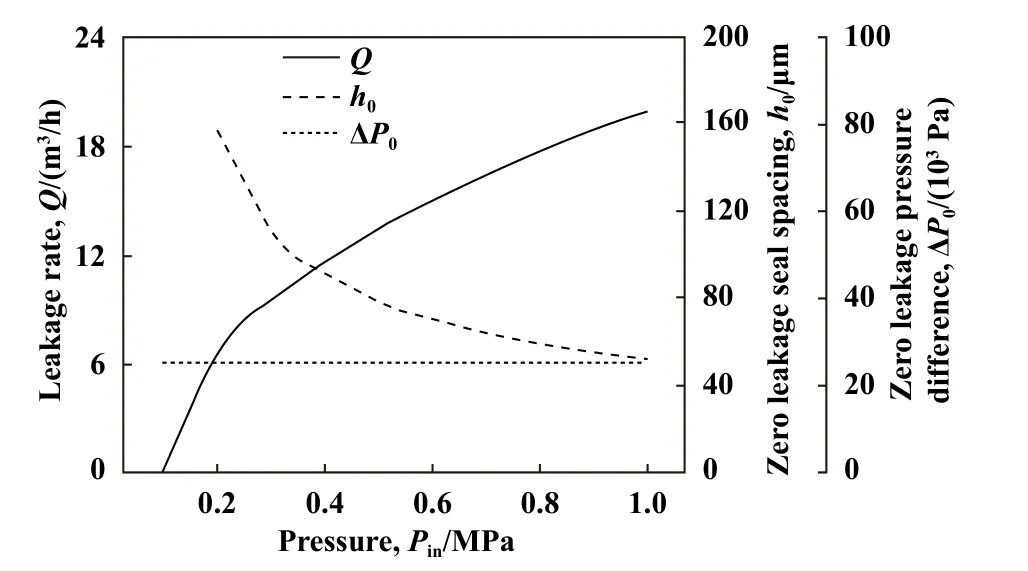
Fig.12 Effects of medium pressure on sealing performance图12 介质压力对密封性能的影响(h=0.1 mm,N=20000 r/min,Z=10,T=300 K)
4.3.2 转速
如图13所示,转速由5 000 r/min增至50 000 r/min,密封泄漏率基本没有变化,无泄漏间距和无泄漏压力则随转速的增大基本呈线性上升趋势,以上规律说明转速的增大有利于新型密封在较大间距和压力下实现零泄漏.由图13还可以看出,泄漏率具有不随转速升高而增大的趋势,这一特性是新型密封区别于多数机械密封的主要特点,也是此类新型密封结构不依赖主轴转速、适于低速甚至停机运行工况的理论基础.
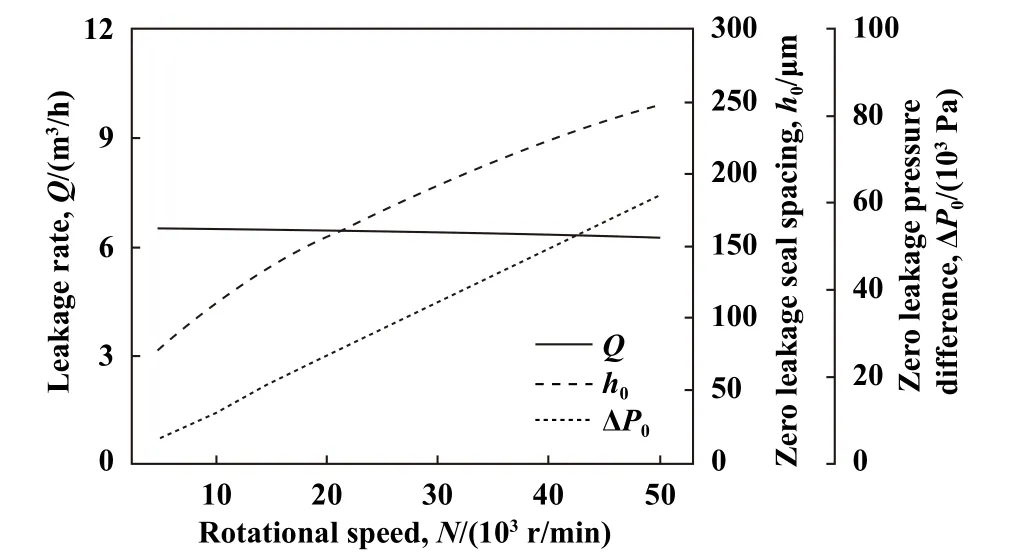
Fig.13 Effects of rotation speed on sealing performance图13 转速对密封性能的影响(h=0.1 mm,Pin=0.2 MPa,Z=10,T=300 K)
4.4 几何参数对密封性能的影响
4.4.1 密封间距
如图14所示,泄漏率随密封间距的增大几乎呈线性增大的趋势,密封间距实际为新型密封三维管道宽度,间距的增大实际就是泄漏通道的增大,是泄漏率迅速升高的主要原因.无泄漏间距根据模型的定义与间距变化无关,而无泄漏压力随密封间距的增大呈先迅速降低后缓慢下降趋势,验证了上文中对通过减小密封间距降低泄漏率的分析判断,由图14可以看出,此工况下对应的临界密封间距约为h=0.2 mm,说明密封间距高于临界值时通过减小密封间距来降低泄漏率的效率最高,当密封间距低于临界值时,采取这一方式的效率不高,且过小的密封间距不利于密封的稳定运行.
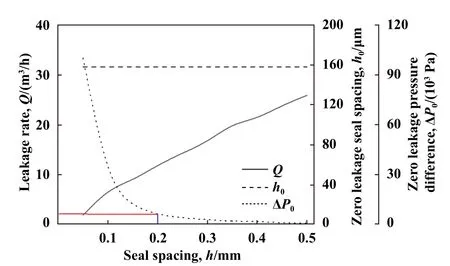
Fig.14 Effects of seal spacing on sealing performance图14 密封间距对密封性能的影响(Pin=0.2 MPa,N=20000 r/min,Z=10,T=300 K)
4.4.2 密封级数
密封级数实际为新型密封的阻流单元个数,如图15所示,随着级数的增大,泄漏率持续降低,而无泄漏间距和无泄漏压力都随密封级数的增大而增大.无泄漏间距的增大,说明密封级数较多时,采用较大的密封间隙即可实现较好的密封效果;无泄漏压力的增大,说明密封级数较多时可以在较高压力下实现密封功能.可见,密封级数越多,新型密封的高压适用能力越好,密封也相对容易,但密封级数的增大同时也会造成密封尺寸的增加,对密封空间有较高要求.所以,应在尽量满足密封要求的前提下采用较少的密封级数,使密封结构更加紧凑.
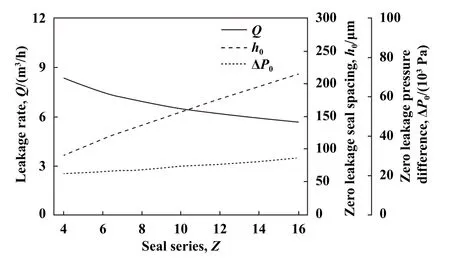
Fig.15 Effects of seal series on sealing performance图15 密封级数对密封性能的影响(h=0.1 mm,Pin=0.2 MPa,N=20000 r/min,T=300 K)
4.4.3 分流角
分流角可以决定新型密封三维管道的内部形状,根据相关文献[12,33],平面特斯拉阀的最佳分流角约为45°~48°.如图16所示,无泄漏间距随分流角的增大而降低,说明随着分流角的增大,需要更小的间距才能实现理论零泄漏;无泄漏压力随分流角的增大而降低,说明随着分流角的增大,只能在相对更低压力下才能实现理论零泄漏.而泄漏率则随分流角的变化有一定的起伏变化,约在48°左右维持较低泄漏水平.综合考虑泄漏率、无泄漏间距及速度因素,对新型密封分流角的选择与平面特斯拉阀一致,亦在45°~48°间选择为宜.
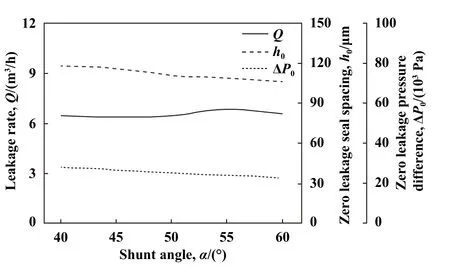
Fig.16 Effects of shunt angle on sealing performance图16 分流角对密封性能的影响(h=0.1 mm,Pin=0.2 MPa,N=20000 r/min,Z=10,T=300 K)
4.5 新型密封标准泄漏设计与计算
实现新型密封的实际应用,应使新型密封在一定压差和转速条件下满足泄漏标准要求,为此,以干气密封技术条件[34]中压缩机用干气密封的动态泄漏率指标为标准,对新型密封进行设计和计算,并列于表3中.

表3 压缩机干气密封件的动态泄漏率,Qmin/(m3/h)Table 3 Dynamic leakage rate of dry gas seal for compressor,Qmin/(m3/h)
上述阶梯型密封存在出口泄漏面积随级数增大而增大的问题,为解决这一矛盾,同时考虑装拆问题,首先将阶梯式通道作对称设计,如图17所示,对称结构可实现出入口界面横截面积一致.进一步将密封外环设计成可通过螺栓连接的两部分,中间采用密封圈密封,内外环3个部分的装配可依次完成.
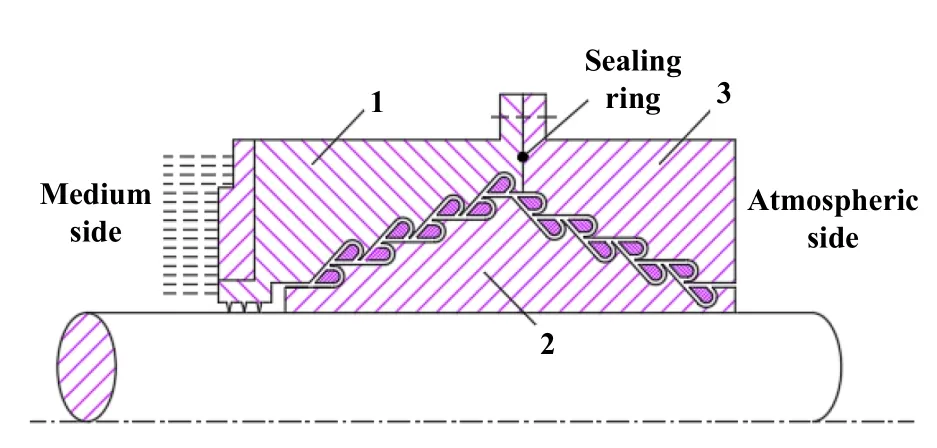
Fig.17 Symmetrical sealing structure图17 对称密封结构
具体几何参数参考表1,N=10000 r/min,D=60 mm,P=0.2 MPa,根据表3中的级数条件,对应的泄漏标准Qmin=0.35 m3/h.由前文中的研究结果可知,通过调节密封间距和密封级数可有效控制泄漏,图18所示为1个大气压力差下,不同级数时的对称式密封结构泄漏率对应不同密封间距的计算结果.可以看出,级数越多,实现标准泄漏时对应的密封间距越大,通过数据拟合,密封级数Z为4、8和12时对应的标准泄漏临界密封间距h分别为0.024、0.026和 0.030 mm(差值计算结果),远高于干气密封气膜条件(0.002~0.005 mm),这一优势可大幅降低密封副接触概率,对提升密封稳定性意义重大.
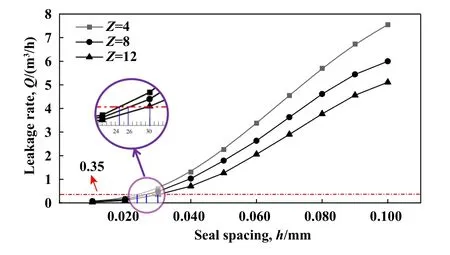
Fig.18 Parameter conditions under standard leakage requirements图18 标准泄漏要求下的参数条件
5 结论
a.基于被动式流体阻塞原理及特斯拉阀结构,对微观密封通道进行三维宏观重构,建立了新型密封结构模型.新型密封通过近毫米级三维管状流场即可实现一定工况下的非接触式密封,且内外环实际为刚性固定,可大幅提升密封副抵御轴向/径向振动的能力.
b.新型密封适用于高密度和高黏度介质工况,随着密度和黏度增加,泄漏率略有下降;新型密封受主轴转速和分流角影响较小,介质压力P、密封间距h及密封级数Z等对密封性能影响较大,可通过降低密封间距、增加级数实现既定密封效果.
c.以干气密封技术条件为泄漏标准与新型密封进行对比,相同工况下,新型密封较干气密封可以在十几倍甚至几十倍密封间距下实现等同泄漏,这一优势对于进一步提升非接触式密封稳定性具有重要意义.

