基于地铁网络的城市人防疏散系统布局研究

罗冰，赵旭东

（北京工业大学城市建设学部，北京 100124）

人防疏散是城市应急疏散的重要组成部分。区别于自然灾害下的疏散，人防疏散是在空袭等蓄意攻击下的紧急疏散，它对疏散有着更高的防护要求。近年来，地铁作为一种新兴的城市公共交通设施，为城市人防疏散提供了一种新的思路。地铁置身城市地下空间，安全性高、运输量大、时效性强，其本身具备的人防属性使其能够在恐怖袭击、空袭等蓄意攻击威胁下安全转移人群。当前国内外对使用地铁进行城市大规模疏散的研究较为匮乏，尚未提出科学的疏散策略。VanLandegen 和Chen基于GIS 和仿真模拟技术，开发了一个利用地铁运输紧急疏散的框架；Abdelgawad 和Abdulhai 将地铁疏散问题设想为传统车辆路径问题的变体，对疏散问题进行了建模。

围绕当前不足，本文提出一种以地铁运输为主导的人防疏散网络，并依托数学模型和算法仿真技术优化网络节点选址布局，以期为以后我国城市开展大规模人防疏散提供方法借鉴与实践参考。

1 系统构建思路

1.1 网络设施配置

本文所构建的地铁疏散网络结构如图1 所示。在地铁疏散模式下，地铁站点充当了公交疏散模式下的集结点，待疏散人群在此集结并转入地下，随后通过地铁网络完成出城转移，到达指定的终端站点出站，再经由地面运输完成最后的末端转移到达安置区。地铁疏散网络覆盖如下四级节点。（1）疏散小区。指位于城市疏散区域内，基于城市人口分布数据和交通路网划分形成的局部疏散需求区域，由若干居民小区组成。（2）地铁疏散前端站点和换乘站点。指地铁疏散网络中的入站站点和换乘站点。（3）地铁疏散终端站点。指疏散人员地下转移的终点，待疏散人群在此进行最后的末端转移到达疏散安置区。（4）疏散安置区。指位于城市边缘的安全地带，是人防疏散的最终目的地。

图1 地铁疏散网络结构示意图

1.2 网络运行分析

人防疏散由政府部门严格组织实施，必须制定高度完善的疏散计划统一指挥。基于本文所构建的疏散体系，重点在于根据疏散人口的出发点—目的地（O-D）流量特征，确定地铁疏散枢纽节点位置并组建合理的疏散链路。

基于上述分析，本文所构建的城市地铁疏散网络涉及以下决策：（1）地铁疏散前端站点的选址；（2）疏散流量与前端站点的分配归属关系；（3）疏散流量在地下转移过程中的乘车路径。

2 网络布局优化方法

2.1 符号定义与假设

分别定义r ∈R，k ∈K，s ∈S，j ∈J，m ∈M 为所有疏散小区、换乘站点、终端站点、安置区和所有备选前端站点的集合，构成点集Q；P 为任意相邻节点之间的路径集合，p ∈P 为地铁隧道链路集合。d ∈D 为疏散流量集合。网络建模参数如下。

（1）参数。drj：疏散小区r 至安置区j 的流量；：地面道路(r,m)，(s,j)和地铁隧道链路p ∈P 的长度；：疏散人群在地面道路(r,m)，(s,j)和地铁隧道链路p ∈P 上的疏散速度；Lk：疏散人群在换乘站点k 处的换乘距离；V0：疏散人群步行速度；n：拟开放的前端站点数量；γmax：前端站点的最大服务半径；φmax：前端站点的最大服务能力；ρmax：换乘站点的最大换乘能力。

（2）决策变量。mx：0-1 变量，若开放站点m 作为前端站点则为1，否则为0；ym rj：0-1 变量，若流量drj归属于前端站点m 则为1，否则为0；zkrj：0-1 变量，若流量drj需要在换乘站点k 处换乘则为1，否则为0；up rj：0-1 变量，若流量drj经过地铁隧道链路p 则为1，否则为0。

为简化模型计算，本文作出如下假设：（1）所有安置区的容纳能力都能满足疏散需求；（2）取距离安置区直线距离最近的地铁站点作为终端站点，不考虑末端转移；（3）疏散小区被分配给唯一的前端站点，两者通过点对点的地面道路直连；（4）所有换乘站点默认开放，且不可被选作前端站点。

2.2 地铁疏散网络布局规划模型

目标函数（1）追求疏散全过程耗时最小化；约束（2）、（3）分别规定前端站点和换乘站点的服务能力限制；约束（4）规定前端站点开放数量；约束（5）规定每个疏散小区归属于唯一的前端站点，且每个前端站点至少为两个疏散小区提供服务。

2.3 模型求解

运筹优化的角度来看，所提出的地铁疏散网络布局规划问题是一类典型的容量受限条件下的选址-分配-路径组合优化问题，其核心是设施选址问题。现有文献表明，此类问题是典型的NP-Hard 问题，无法在多项式时间内求得最优解。为此，本文采用文献所提出的一种改进的自适应免疫克隆选择算法对设施选址问题进行迭代寻优，并结合Dijkstra 算法确定疏散流量在地铁网络中的最短路径。

3 案例分析

3.1 场景设置

以南京市人防疏散为案例背景，地理信息如图2所示。疏散区域面积约195 平方公里，疏散对象为疏散区域内常住人口的15%约41 万人。根据南京市街道行政区域划分和城市交通路网，将疏散区域划分为195 个疏散小区，分配给位于城市边缘的4 个安置区，得到规模为195×4的疏散流量矩阵。依托南京地铁2、3、4 号线为骨架组建地铁疏散网络，其中包括70 个普通站点和3 个换乘站点，备选前端站点36 个。表1 列出了仿真模型主要参数取值，部分依据城市交通运营的经验数据拟定。

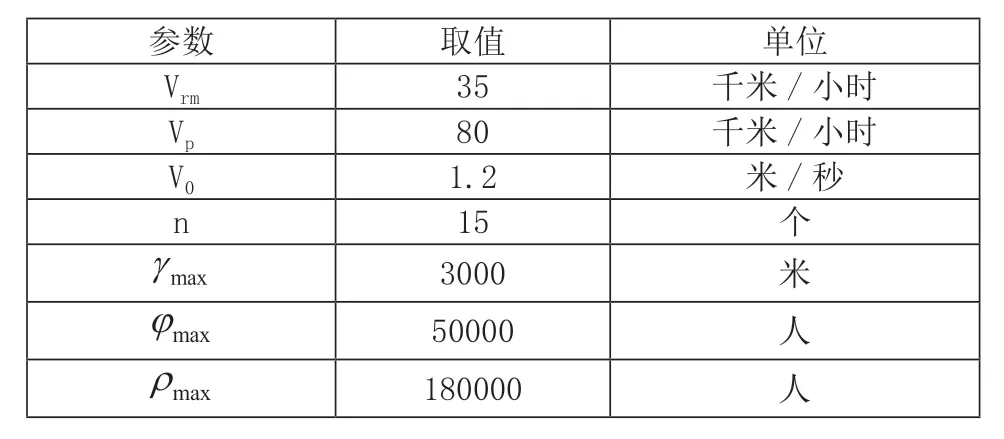
表1 仿真模型主要参数设置

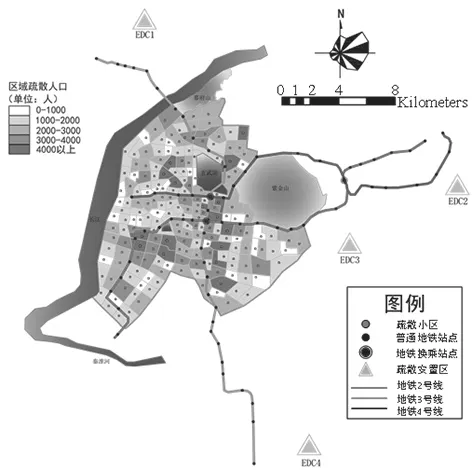
图2 南京市疏散案例

3.2 仿真优化结果

设置改进免疫克隆选择算法的初始种群规模为100，记忆库容量为50，多样性评价参数为0.9，变异概率为0.15，迭代次数为100，利用上述算法对模型进行优化求解。

表2 列出了南京市人防疏散案例中的地铁疏散网络布局优化结果，确定选取的前端站点分别为2 号线的下马坊站、西安门站、云锦路站、兴隆大街站、元通站和雨润大街站；3 号线的上元门站、小市站、南京站、夫子庙站、雨花门站和大明路站；4 号线的龙江站、草场门站和云南路站。其中服务疏散小区数量最多的站点为西安门站，为21 个，其服务的人口数量最多为47870 人；服务疏散小区数量最少的站点为雨润大街站，为2 个，其服务的人口数量最少为2578 人。由此可见，本文所采用的模型求解算法能够有效解决前端站点的选址优化问题，并实现疏散需求的合理分配，筛选地下运输路径。

表2 南京市案例仿真布局优化结果

4 结语

针对城市大规模人防疏散问题，本文开拓性地提出将地铁网络与之结合，构建地铁疏散网络，并对其进行系统设计与网络规划。建立了混合整数规划模型优化网络设施选址布局，采用一种改进自适应免疫克隆选择算法和Dijkstra 算法相结合的组合算法对模型进行求解，通过南京市人防疏散案例进行仿真实验。结果表明，本文所提出的网络布局优化方法能够快速实现地铁疏散网络的优化布局，为使用地铁进行城市大规模人防疏散提供了方案借鉴。