基于GIS构建邯郸市某区SWMM雨洪模型的方法研究
何立新,宋晓旭,雷晓辉,张 峥
(1.河北工程大学水利水电学院,河北 邯郸 056038;2.河北工程大学能源与环境工程学院,河北 邯郸 056038;3.河北工程大学河北省智慧水利重点实验室,河北 邯郸 056038)
相关资料显示,2010—2016 年的7 a 间,全国有73%的地级市遭遇雨洪问题,城市内涝频繁发生,97%的省会城市发生约208 起城市积涝[1]。想要改变城市“看海”的现状,城市雨水管网系统的改造和完善是关键。然而,我国大部分城市雨水管网系统设计标准低,抵抗高重现期极端暴雨能力低。应用雨洪模型模拟不同重现期降雨的城市内涝过程,可直观分析现状雨水管网运行情况,为改善城市排水系统、解决城市内涝问题提供思路。周玉文等[2]基于SWMM 模型模拟不同重现期下的城市内涝,通过对比分析整个管网的超载、溢流情况,评估了城市排水能力。陈睿星等[3]通过联合AutoCAD 和GIS,建立SWMM 模型的研究已得到了广泛运用。但基于实测数据和参数经验取值搭建模型,对于实测资料缺乏或无校核资料搭建模型的方法研究还不够充分,并且GIS 和SWMM 的耦合、AutoCAD 和SWMM 的耦合等,均基于SWMM 源代码的二次开发,技术门槛高,不宜推广,限制了雨洪模型的发展。本文以河北省邯郸市某区为例,基于雨水管网施工CAD 图,详细介绍了模型搭建过程和模型参数的计算方法,在缺乏校核资料的情况下验证模型的准确性,以期为设计人员提供更详细、更简单可行的雨洪模型搭建方法。
1 雨洪模型搭建
1.1 SWMM模型基本介绍
SWMM 模型跟踪时间步长构成的模拟时间段内每一个汇水区内产生的径流量,每一个管渠中的流量、水深。管道中的雨水以动态波[4]从管道的上游输送到下游,通过圣维南方程组[5]中水流运动方程和动量方程,求解管渠流量和节点水头。运动方程和动量方程分别为:
式(1)和式(2)联立,即可得到管渠流量求解的偏微分方程式(3)和节点水头求解的偏微分方程式(4):
式中:A为管道的横截面面积(m2);t为水流动的时间(min);Q为流量(m3∕s);x为水流动的距离(m);H为管道水的落差水头(m);g为重力加速度(m∕s2);Sf为管道的粗糙系数;U为流速(m3∕s);AsN为节点的蓄水表面积(m2);AsL为管段连接节点的表面积(m2)。
1.2 GIS管网创建
搭建SWMM 模型前,首先要处理管网的空间信息,这就需要利用GIS 软件,创建GIS 管网。GIS 空间关系中的顺序关系理论、度量关系理论和拓扑关系理论为创建GIS管网提供了理论支撑[6]。
排序关系理论[6]描述点或线在空间中的某种顺序,以东方向为例,具体表达形式为:
式中:East(Pi,Qj)为正东方向(Pi,Qj)点坐标;North-East(Pi,Qj)为东北方向(Pi,Qj)点坐标;Restricted-Eas(Pi,Qj)为其余东部方向(Pi,Qj)点坐标;South-East(Pi,Qj)为东南方向(Pi,Qj)点坐标。
其余方向可依此类推。
度量关系理论使用空间运算最广的欧式距离公式[7]计算,具体表达形式为:
式中:d(X,Y)为坐标的欧氏距离;xi、yi为坐标值;n为空间维数。
拓扑空间关系理论[7]是指空间目标的相邻和联通关系。拓扑关系形式使用最广的4 元组模型[8]描述,具体表达形式为:
式中:R4(A,B)为4元矩阵;∂A为元素所在的边界;A0为元素所在的内部;∂B 为另一个元素所在边界;B0为另外一个元素所在的内部。
对于SWMM 模型建立所需要的数据库文件而言,空间位置信息是其中的关键,详见表1。将图1通过上述的计算得到图2[9]。利用拓扑空间关系理论,检查相邻的管线和节点的联通关系合理性,删除孤立的管线和节点[10]。
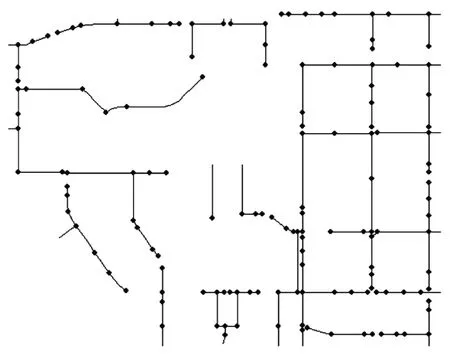
图2 GIS管网

表1 建模数据与理论
1.3 降雨数据计算
根据《室外排水设计标准》(GB 50014—2021)[11]和暴雨强度公式,分析芝加哥雨型理论[12],计算不同重现期的降雨数据。暴雨强度表达形式为:
经简化,暴雨强度表达形式为:
式中:A1、C、b、n、a为参数,其中a=167A1(1+ClgP);i为平均降雨强度(mm∕h);q为降雨强度(mm∕h);t为降雨历时(min);P为降雨频率。
在雨水管网系统设计过程中,还涉及峰值比例r([0,1]),将r 代入式(9)中,可将降雨过程分成峰值前降雨和峰值后降雨[1,12],以降雨时间来表达,即:
式中:t为降雨发生的所有时间和(h);tb为降雨达到最大值时所发生的降雨时间(h);ta为降雨达到最大值后至降雨结束所用的时间(h);r为峰值系数。
进而,可求出历时tb时间的降雨总量公式为:
式中:Pb为历时tb时间的降雨总量(mm);其余变量含义同上。
由此,降雨高峰时期前的降雨强度可表示为:
式中:ib为tb时间的降雨强度(mm∕h);其余变量含义同上。
降雨高峰时期后的降雨强度可表示为:
式中:ia为ta时间的降雨强度(mm∕h);其余变量含义同上。
通过上述计算,可以求出降雨时序(如图3 所示)和相应的降雨量(详见表2)。
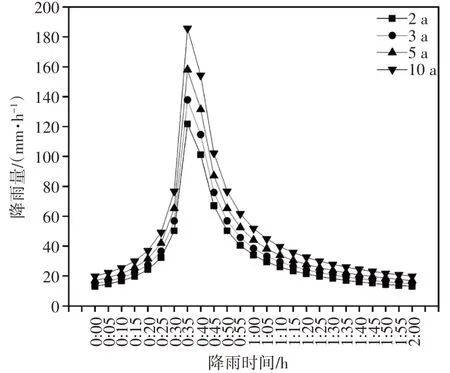
图3 降雨时序
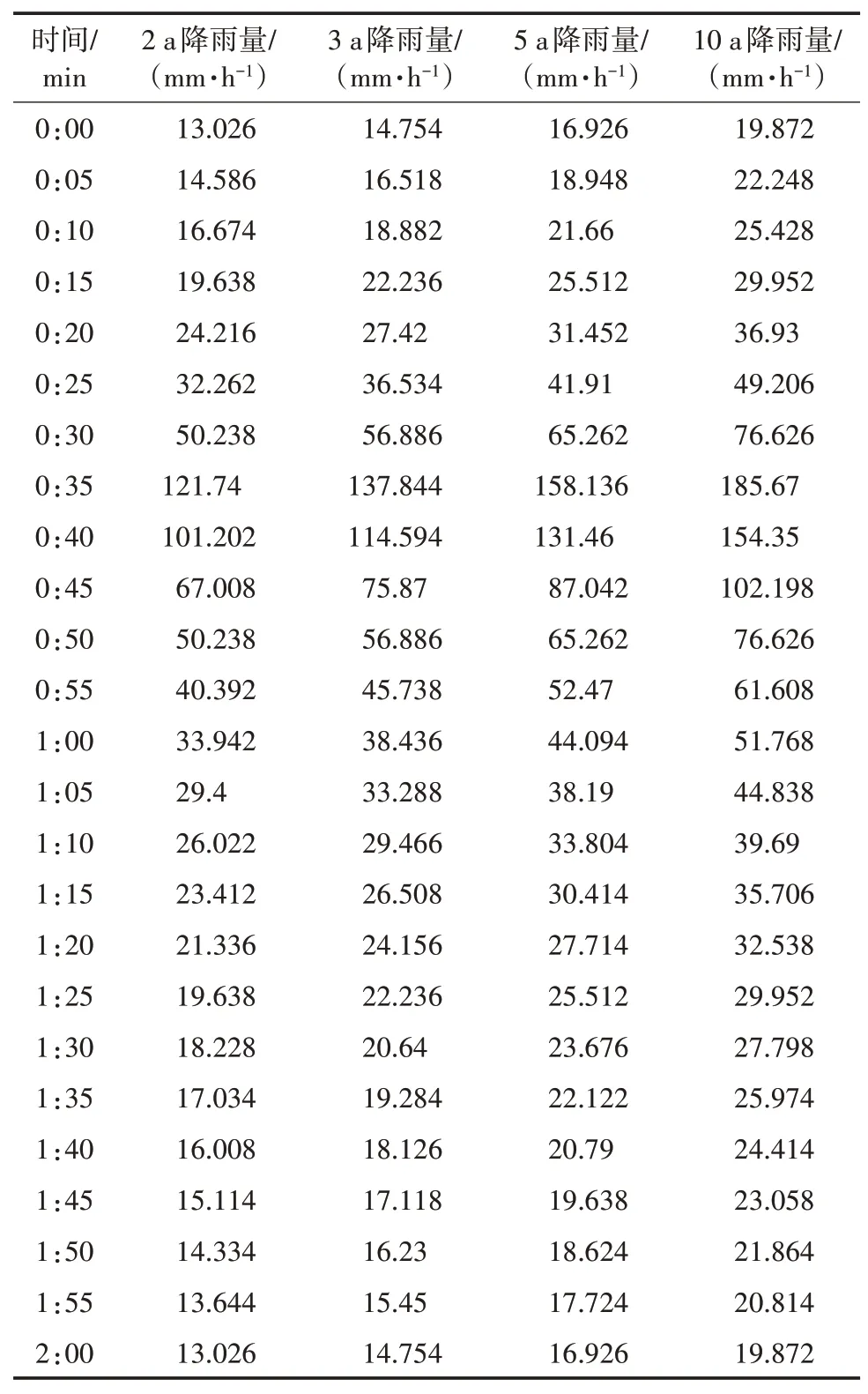
表2 降雨数据
1.4 划分子汇水区间
基于空间目标的Voronoi 区域理论[13]划分子汇水区间,其效率高、效果好,可避免人工绘制产生的划分不规则、子汇水区水流流向紊乱的缺点。Voronoi区域理论利用数学表达形式表示:
式中:Ov为Oi到Oj最短距离的点的集合;distance(p,Oi)为p到Oi的欧氏距离;distance(p,Oj)为p到Oj的欧氏距离。
经Voronoi 区域理论形成Voronoi 图[14],即为泰森多边形,按照研究区域的边界图裁剪子汇水区,最终形成如图4所示子汇水区。
1.5 子汇水区平均坡度
集水区的坡度即可作为地表径流到排放口的平均坡度的表达。地型较简单、研究区域小的子汇水区坡度计算公式为:
式中:i为子汇水区坡度(%);hL为高程(m);L为水流长度(m)。
根据研究区域的地面高程文本数据转换成点高程数据[15],利用3D Analyst Tools和Spatial Analyst Tools-Surface 绘制TIN 数据(如图5 所示)、高程数据(如图6 所示),利用上述公式计算子汇水区坡度(详见表3)。

图5 TIN数据

图6 DEM高程

表3 部分子汇水区间的平均坡度
1.6 子汇水区特征宽度
周毅等[16]介绍了SWMM 子汇水区域宽度参数的估算方法,阐述了式(17)的方法与SWMM 设计手册的解释最为接近。因此,本研究区域基于下列公式计算特征宽度,部分计算结果详见表4。
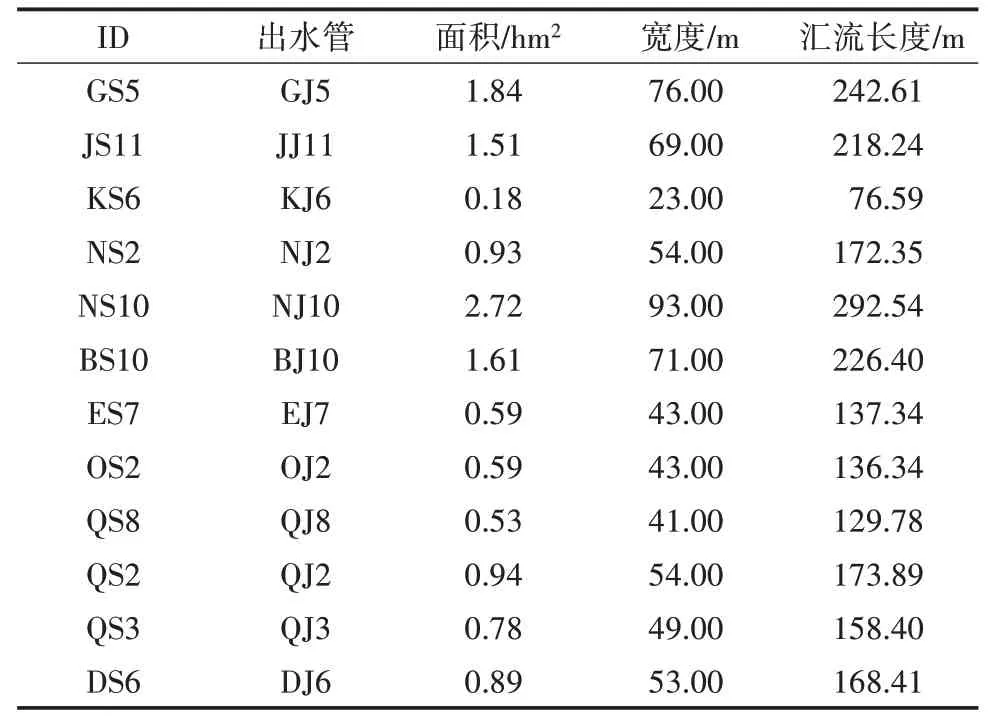
表4 部分子汇水区间特征宽度
式中:Width为子汇水区的特征宽度(m);Area为子汇水区的面积(m2);FlowLength为子汇水区的汇流长度(m)。
1.7 子汇水区不透水百分比
不同土地类型面积占不透水区百分比和不透水百分比计算公式分别为:
式中:w为不同土地利用类型的面积(m2);wi为不透水百分比(%);a为径流系数;n为土地利用类型种数;q为不透水土地利用类型种数;wq1为不同土地类型面积占不透水区百分比(%)。
土地利用类型如图7 所示,精确地面分类径流系数取值[11]详见表5。基于以上数据,计算出各子汇水区对应的不透水区百分比,详见表6。

表5 精确地面分类径流系数取值
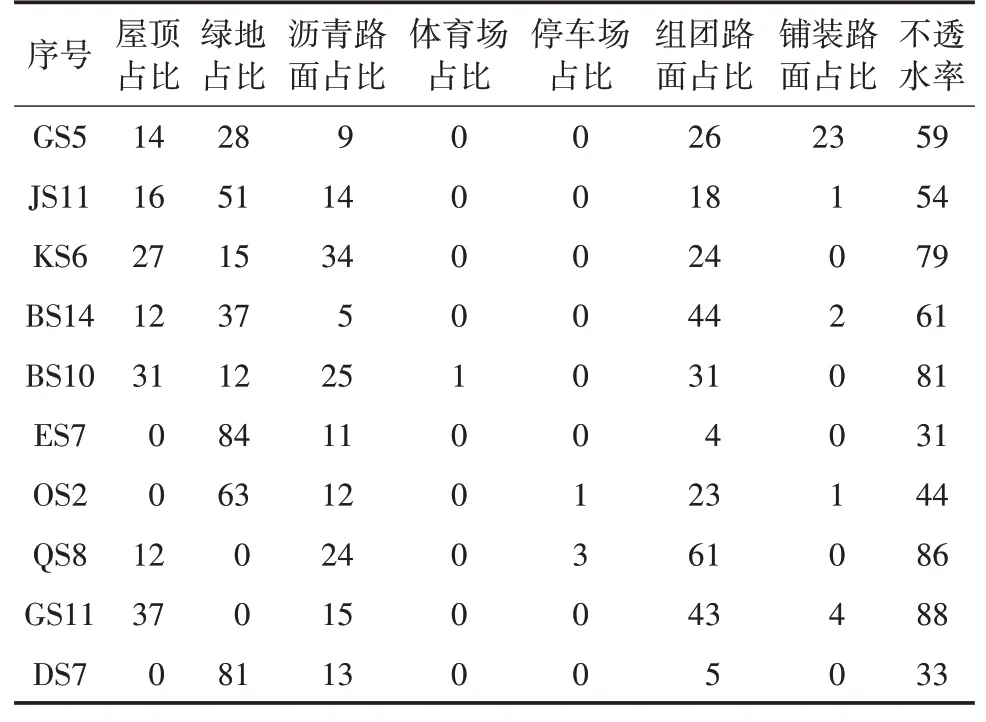
表6 部分子汇水区的不透水百分比%
1.8 模型参数确定
1.8.1 子汇水区曼宁系数
以子汇水区GS5 为例,利用式(20)计算不透水区曼宁系数为0.012,详见表7。而本研究区域的透水区只用草地,故不透水区曼宁系数均为0.24。
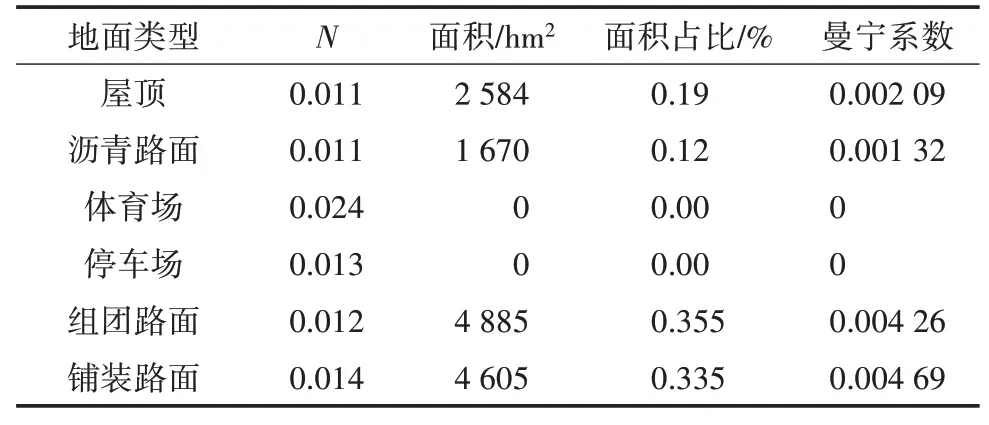
表7 GS5不透水区曼宁系数
式中:Nt为不透水区曼宁系数;N为不同地表径流计算的曼宁N值;wq2为特定子汇水区的不透水面积百分比(%)。
1.8.2 地表下渗
地表下渗的基础是Horton 产流理论[17],它指出土壤吸水的多少会与土壤湿度成反比,当土壤湿度较小时,土壤会吸收更多的雨水;反之,土壤吸水容量很低。Horton下渗模型表达式为:
式中:F(tp)为tp时地表下渗能力(mm∕h);tp为时间(h);fp为雨水渗透地表的能力(mm∕h);f∞为雨水渗透地表能力的最小或者雨水渗透地表的饱和值(mm∕h);f0为雨水渗透地表能力的最大或者雨水渗透地表的初始值(mm∕h);kd为入渗系数;e()为底数为e的指数函数。
式(21)描述了和Horton产流理论一样的理论内容,即当雨强≤下渗时,不会产生地表径流;反之,雨水超过土壤吸水容量时达到饱和,形成地面径流。
Horton 下渗模型参数分为最大入渗速度、最小入渗速度和衰减系数。利用式(22)计算子汇水区GS5的最大入渗速度和最小入渗速度,结果详见表8。
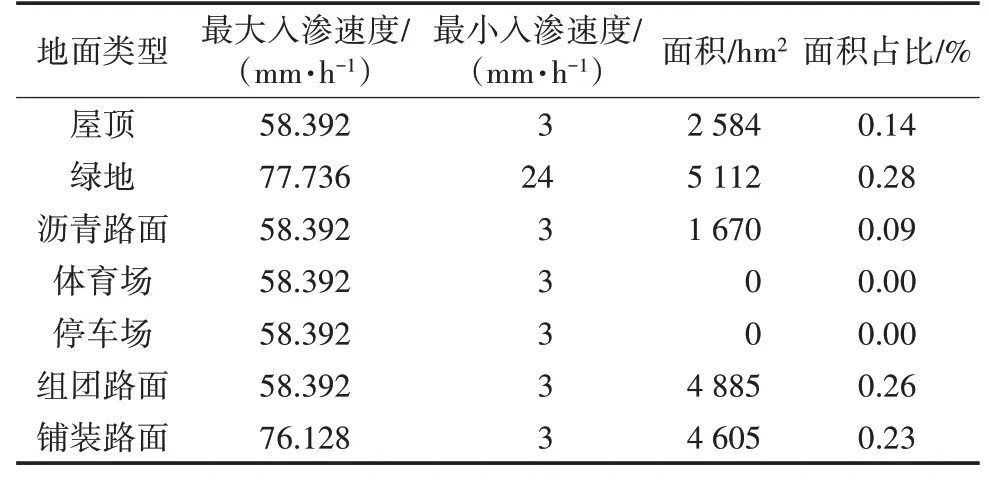
表8 子汇水区GS5最大入渗和最小入渗速度
式中:Nmax为最大入渗速度(mm∕h);fmax为不同地面类型的Horton 下渗模型最大经验参数;wq1为不同土地类型面积占总面积百分比(%)。
1.9 SWMM模型搭建
将排水管网所需要的建模数据通过图8 所示的.inp文件格式输入SWMM 模型[18]。SWMM 模型的输入文件,包含了工程文件、界面文件、降雨文件、气象文件和时间序列文件,为模型的搭建提供必须的支持数据[19]。

图8 .inp文件要素
2 模型参数的率定
针对缺乏研究区域实测校准数据的问题,刘兴坡等[20,21]提出了一种实测校准数据不全或者没有的情况下验证模型契合研究区域高低的率定方法。在本研究中,不透水区域覆盖面积约为67%,符合表9中建筑较密集区域要求。将不透水区加权计算确定本研究区域的综合径流系数为0.618 5。以3 a 一遇的降雨为基准降雨,经过表10中的7次迭代调整,选取第5 次校核系数为模型参数,最后利用1、5、10 a的降雨数据复核,结果符合综合径流系数误差范围,模型参数准确性高。

表9 综合径流系数取值范围
3 不同降雨情境下模拟结果
3.1 不同降雨情境下径流系数分析
SWMM 模型在不同重现期下执行成功后,分析研究区域的总降雨量、总径流量、入渗量以及径流系数变化情况[22],详见表11。分析图9 可知,在降雨重现期不断增大的情况下会得到3个结论,分别是:①总降雨量、渗入损失量、地表径流都发生了不同程度增大,分别上升了52.52%、3.11%、73.15%。②渗入损失经过快速入渗阶段和相对稳定阶段后对降雨量的敏感性降低。原因在于,不同强度的暴雨降落在地面时所含动能也不一样,呈正相关关系。含有较大动能的雨滴降落地面,会形成更多的地面泥浆
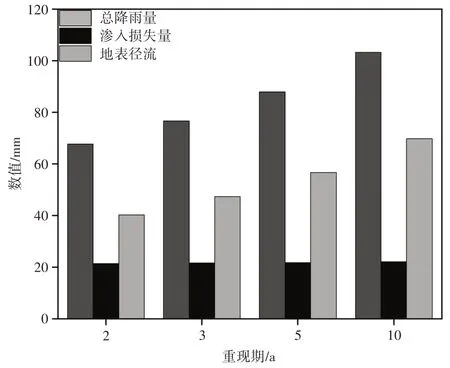
图9 降雨数据变化
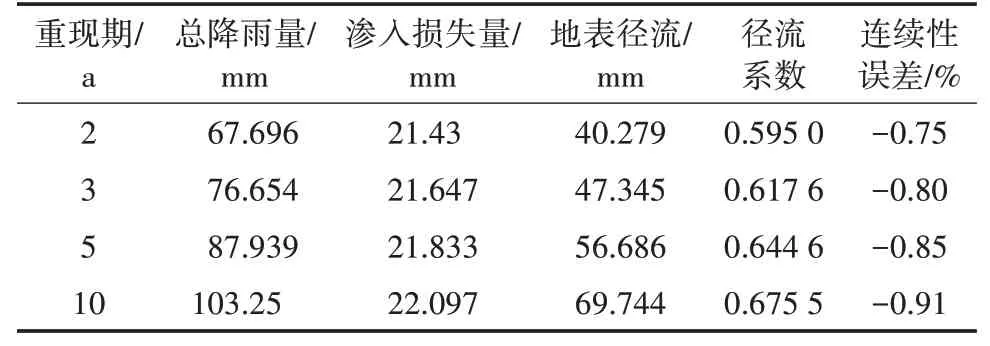
表11 降雨数据汇总
3.2 不同降雨情境下积水分析
SWMM 模型通过对不同重现期下的雨水强度进行模拟,可在结果分析中对每一个管道和节点的进流深度、满流时间进行分析,进而确定管道和节点的超载、溢流以及位置分布等情况[22],模拟结果详见表12—13。由表12可知,降雨强度与超载管道数量和地表径流,通过雨水冲刷会在土壤表面形成不透水表层,使土壤孔隙率下降,而土壤孔隙率是影响入渗的关键因素,且成正相关关系,因此使入渗量比例减小[23,24]。③径流系数的不断增加。原因在于,地表径流在降雨量中占比不断增大以及研究区域对洪涝风险抵御能力逐渐减小。其中,NC10管段的超载时间最大,分别是1.38、1.41、1.44、1.48 h,绘制NC10在不同降雨情境下进水深度和降雨强度之间的变化关系,如图10所示。呈正比,但超载时间≥1 h 管道比例保持在一个较小的范围,这说明管道的排水能力在暴雨强度增大的情况下有一定的提升,原因在于雨量的增加使管内流速变大,提高了管道的流通能力。
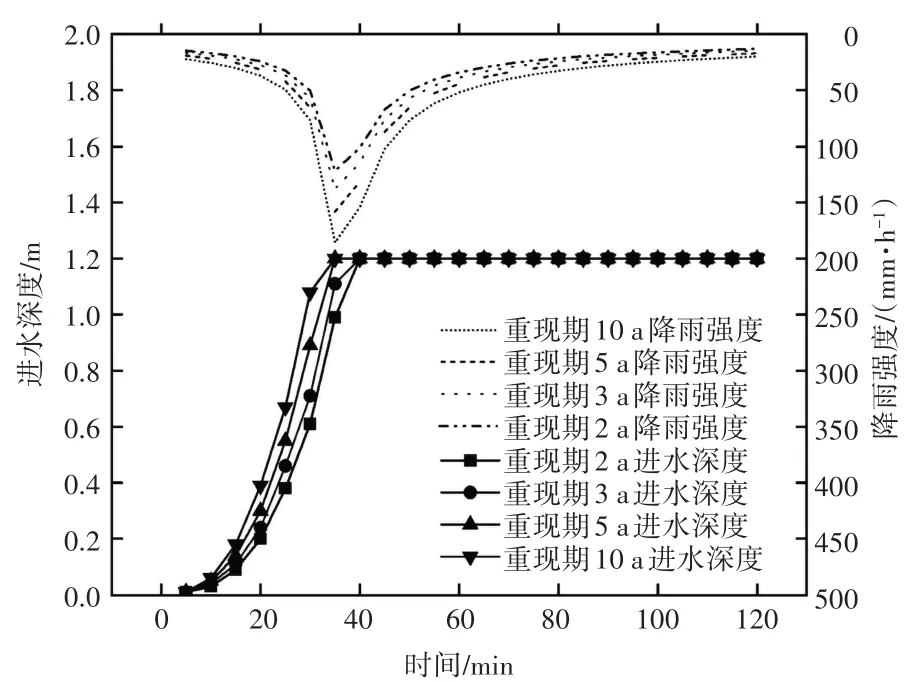
图10 NC10管段进水深度与降雨强度之间的变化
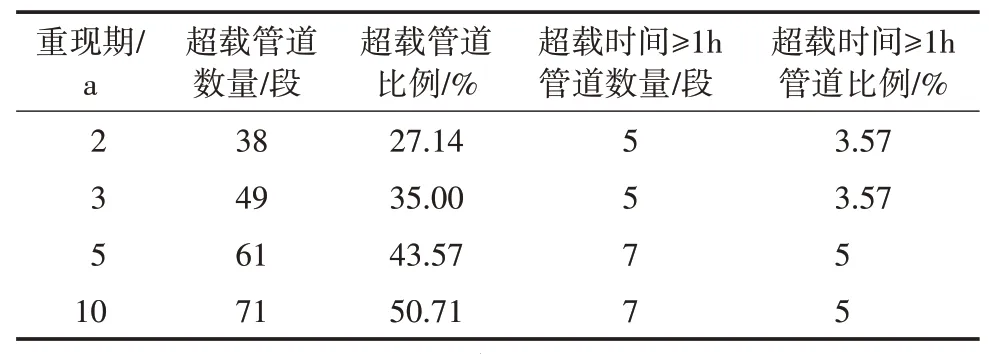
表12 管段超载分析
由表13 可知,随着降雨强度增大,检查井超载数量和超载时间数量都在增加,但超载时间≥1 h 的检查井的比例保持较低的水平,均在10%以内,说明随着降雨强度的增大,检查井即使发生积水,仍可在较短时间内消散,不会造成洪涝。

表13 检查井的积水和超载情况
4 结论
(1)在建模技术上,整个建模过程只基于雨水管网施工CAD 图,并使用.inp 文件方法建立SWMM 模型,通过综合径流系数法验证了模型的高准确性、强适用性,避免了使用多个软件和GIS 源代码的二次开发,为缺少代码开发的技术人员提供了更为简单可行的方法,为城市雨水管网系统模拟及评估提供了参考。
(2)在模拟分析上,通过SWMM 模型可清晰地看到研究区域存在的径流量、管道超载、节点积水的区域,并且在3 a 一遇的基础上模拟了2、5 和10 a 的降雨情境,可以看出研究区域的雨水管网系统可有效抵御3 a 以内的降雨强度,而在5 a 一遇和10 a 一遇的降雨强度下会出现不同数量的超载管段和溢流节点,且随着降雨重现期的增大,超载管段数量和积水节点数量均增多,超载管段两端的节点易产生溢流。通过比对超载管道和未超载管道可以看出,超载时间长的管段其上下游满流时间长,成正比关系,相应的节点积水时间也比较长,具有正相关关系。

