一种基于双星干涉仪相位差和时差融合的空中动目标跟踪方法

徐海源，苏成晓，党卫，高凤辉

（北京遥感信息研究所，北京 100011）

0 引言

星载无源定位系统具有覆盖范围大、不受地域限制等优点，在辐射源监测和定位中得到了广泛应用。其中，单星无源定位系统具有成本低、技术成熟等优点［1-3］，利于灵活配置和大规模组网应用。针对空中辐射源，单星定位系统需要假设高程进行定位，将带来较大的定位误差［4］。采用三星定位体制，通过增加测向等信息，并利用跟踪滤波方法，可实现空中目标三维位置和速度的高精度估计［5-6］。

针对双星体制对空中目标的定位，文献［7］采用主星高精度测向和双星时差联合实现空中目标高精度定位，但需要较高的测向精度，传统的干涉仪测向系统难以满足要求。针对单星测向定位体制的多颗卫星对同一目标存在共视的情况，文献［4］提出了基于双星测向结果求解空中目标位置的方法，典型场景下定位误差仿真结果为几千米，可提高空中目标的定位精度，但基于定位结果难以实现目标高程和运动速度的高精度估计。

本文针对2颗安装二维正交干涉仪的单星定位系统对空中目标共视的应用场景，从辐射源信号参数测量模型和处理流程出发，提出了基于双星干涉仪相位差和时差融合的空中动目标定位跟踪方法，以期提高空中目标的位置和速度估计精度。

1 双星干涉仪相位差和时差融合跟踪处理流程

1.1 双星定位系统辐射源信号参数测量模型

2颗卫星均安装二维正交干涉仪的测向定位系统，在共视区域内接收到空中目标辐射的信号，每颗卫星可测得辐射源信号到达接收天线的相位差信息，基于2颗卫星获取的信号参数还可以进一步得到时差信息。双星定位系统示意如图1所示。

图1 双星定位系统示意

在单星二维正交干涉仪测向系统中，为简化描述，假设星体坐标系与干涉仪坐标系重合，天线A、B分别安装于星体坐标系Y、X轴，Z轴对地，天线O位于星体坐标系原点。原始观测量为辐射源信号到达天线A和天线B与天线O之间的相位差，分别记为φA、φB。假设星体坐标系下的辐射源位置坐标为(xb，yb，zb)，则φA、φB可表示为［2］：

式中，n=，其中d为干涉仪基线长度，λ为信号波长。

对于2颗卫星收到的辐射源同一脉冲信号，其时差τ可表示为：

式中，c为电磁波传播速度，r0、r1分别为辐射源与卫星0、卫星1的距离。

1.2 定位跟踪处理流程

本文针对运动目标辐射源发射脉冲信号的情况，考虑2种定位跟踪处理流程：一种是基于单脉冲相位差测量数据和时差测量数据直接进行跟踪滤波；第二种是针对多个脉冲序列按一定时间节拍进行相位差和时差参数估计后，再按时间节拍进行跟踪滤波。

基于参数估计理论，直接采用原始测量数据进行跟踪滤波能够得到更高的精度，但在实际应用中，考虑到处理效率，经常采用第二种处理方式。2种处理流程如图2所示。

图2 2种定位跟踪处理流程

2种处理流程的主要差别在于是否增加按时间节拍进行参数估计的环节，这里采用最小二乘法进行相位差和时差估计。

1.3 基于最小二乘法的相位差和时差估计

由于空中目标与2颗卫星之间存在较大的相对运动速度，因此，在一定时间段内对相位差和时差进行估计时，需要考虑切向相对运动速度带来的相位差变化率和径向相对运动速度带来的时差变化率带来的影响［3，8］。

1）相位差估计

利用观测时间段内的N个脉冲的相位差测量数据估计初始时刻的相位差φ0及相位差变化率φ̇，最小二乘估计法为：

式中，φ=[φ0，φ1，…，φN-1]T为相位差测量数据构成的向量，H为N×2矩阵：

2）时差估计

设观测时间内2颗卫星均接收到同一辐射源的N个脉冲，脉冲配对后第k个脉冲对的到达时间（TOA）为t0k和t1k，τk=t1k-t0k表示第k个脉冲到达2个观测站的时间差。

记τ=[τ0，…，τN-1]T为时差序列测量数据构成的向量，则采用最小二乘估计法对初始时刻时差τ0及时差变化率τ̇的估计公式为：

式中，H为与式（4）相同的N×2矩阵。

1.4 相位差及时差估计精度

最小二乘估计的方差为：

对于相位差估计，R=，其中为单脉冲的相位差测量方差。因此，相位差估计的方差可以进一步简化为P=(HTH)-1。

假设相邻2个脉冲的时间间隔Δtk=tk-tk-1相等，且等于Δt，通过进一步数学变换可得：

由此得到初始相位差φ0的估计误差方差为=2(2N-1)/(N(N+1))。

2 双星干涉仪相位差和时差融合跟踪模型

2.1 状态方程

考虑空中目标运动模型为匀速模型（CV），定义k时刻的状态量为WGS-84坐标系下的目标位置及速度，即Xk=[xkykzkvxkvykvzk]T，则状态方程为：

式中，A为状态转移矩阵，定义为：

式中，Δt为观测时间间隔，wk-1为过程噪声，其均值为0，协方差矩阵为Qk-1。

对于CV模型，状态噪声协方差Qk-1表示为［9］：

式中，I3为三维单位阵，为速度在各方向的随机误差的方差。

2.2 观测方程

为了在WGS-84坐标系下进行目标状态跟踪滤波，首先需要将式（1）的相位差观测量转换到WGS-84坐标系。记星体坐标系相对WGS-84系的旋转矩阵为M，其推导过程参见文献［6］。记WGS-84坐标系下卫星位置为（xs，ys，zs），辐射源位置为(x，y，z)，由于

式中，mij为坐标旋转矩阵M中的元素。于是，式（1）可表示为：

记2颗卫星获得的辐射源信号相位差测量数据（或估计数据）序列为φ0，Ak、φ0，Bk、φ1，Ak、φ1，Bk，时差测量数据（或估计数据）序列为τk，则观测方程为：

式中，(xi，k，yi，k，zi，k)为WGS-84坐标系下的卫星位置，i=0，1；(xk，yk，zk)为WGS-84坐标系下辐射源的位置，ri，k=((xk-xi，k)2+(yk-yi，k)2+(zk-zi，k)2))1/2。mij为卫星0星体坐标系相对于WGS-84坐标系的旋转矩阵M的元素；m'ij为卫星1星体坐标系相对于WGS-84坐标系的旋转矩阵M'的元素；vk为均值为0，协方差矩阵为Rk的高斯白噪声。

在基于单脉冲参数进行跟踪滤波过程中，噪声协方差Rk=diag分别为单脉冲时差、相位差测量误差的方差。

若按照一定时间节拍采用脉冲积累先估计时差、相位差再进行跟踪滤波，则需要根据积累脉冲数量N计算时差、相位差的误差，根据1.4节分析可知，Rk=2(2N-1)/(N(N+1))·diag()。

3 EKF跟踪算法

由于观测方程为非线性方程，需要采用非线性滤波方法提高对运动目标位置和速度的估计精度。本文采用扩展卡尔曼滤波（EKF）进行空中运动目标跟踪。

3.1 滤波初始化

1）目标状态初始值

可以通过假定高程，采用其中一颗卫星单星测向定位的方法计算得到初始位置(x0，y0，z0)［2］。目标初始速度可以设置为(0，0，0)，即目标状态的初始值为X0/0=[x0y0z0000]T。

2）初始预测协方差矩阵

基于单星干涉仪相位差测量误差、高程假设误差、卫星位置误差等信息，可以计算得到初始点定位的协方差矩阵P1［2］。假定目标可能的最大航速为vmax，记P2=diag。设置初始预测协方差矩阵P0/0=diag(P1，P2)。

3.2 EKF跟踪滤波步骤

基于上文建立的目标状态方程和观测方程，对目标进行EKF跟踪过程如下：

1）目标状态预测

2）协方差矩阵预测

3）计算Zk在预测点处的雅克比矩阵

4）卡尔曼增益矩阵计算

5）更新目标状态

6）更新协方差矩阵

需要说明的是，最简单的二维正交干涉仪测量的相位差会出现模糊现象，在实际应用中可以采用多基线或长短基线结合等方法解模糊。在本文算法和步骤的描述中，均假定相位差观测量为无模糊值。

4 仿真分析

为验证提出的基于双星干涉仪相位差和时差融合的空中运动目标跟踪方法的有效性，建立典型场景进行了仿真分析。2颗卫星轨道高度均为700 km，星间距80 km，每颗卫星上均安装二维正交干涉仪，基线长度3 m；目标高程为10 km，速度为300 m/s的匀速直线运动；目标辐射源频率为3 GHz，辐射源脉冲重复频率（PRF）为100 Hz。卫星姿态测量误差0.05°（3轴，1σ），干涉仪相位差测量误差为20°（1σ），时差测量误差为50 ns（1σ）。在双星共同覆盖区域内选取一个目标位置，对基于脉冲测量参数直接进行EKF滤波的处理方法和基于时间节拍参数估计后进行EKF滤波的处理方法分别进行100次Monte-carlo仿真，并进行比较。同时，针对文献［4］的双星测向定位和文献［7］的单星测向+双星时差定位体制下的跟踪滤波情况也进行了仿真比较。

1）单脉冲测量数据直接EKF仿真结果

基于单脉冲测量数据直接EKF滤波方法，针对观测量分别采用双星干涉仪相位差+时差、双星干涉仪相位差、单星干涉仪相位差+时差3种情况，对目标位置（含高程）、航速和航向估计误差进行了仿真比较，如图3—5所示。

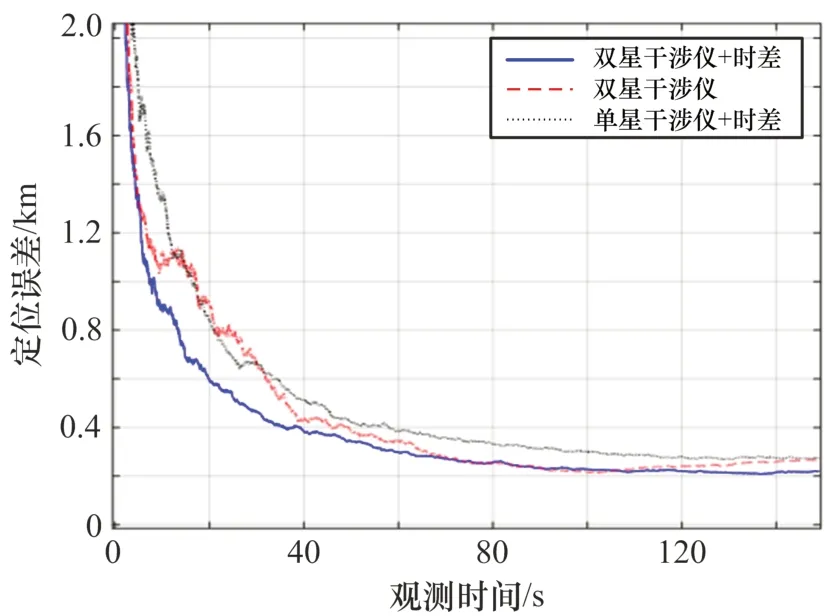
图3 单脉冲直接EKF定位误差

从图3可以看出，本文提出的基于双星干涉仪相位差+时差观测量的EKF滤波方法相比另外2种方法具有更快的收敛速度和更高的位置估计精度，在仿真场景下跟踪10 s后定位误差小于1 km（含高程误差），跟踪100 s后定位误差接近0.2 km（含高程误差）。

从图4—5可以看出，观测量采用双星干涉仪相位差+时差、单星干涉仪相位差+时差与采用双星干涉仪相位差的EKF滤波方法相比具有更短的速度和航向估计收敛时间，原因在于卫星和目标之间存在较大的相对速度，原始观测量中的时差参数隐含了时差变化率信息，体现出了目标运动速度相关信息。

图4 单脉冲直接EKF速度误差

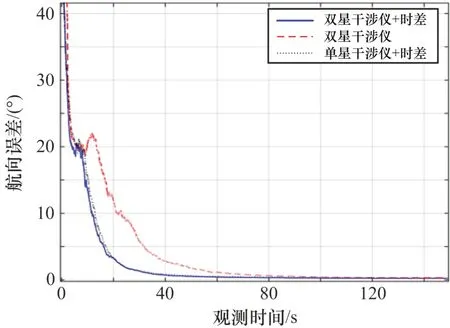
图5 单脉冲直接EKF航向误差

2）基于时间节拍参数估计的EKF仿真结果

基于上述仿真参数，采用1 s时间节拍进行参数估计（即每个节拍100个脉冲）后再进行EKF的方法，针对观测量分别采用双星干涉仪相位差+时差、双星干涉仪相位差、单星干涉仪相位差+时差3种情况，对目标位置（含高程）、航速和航向估计误差进行了仿真比较，如图6—8所示。

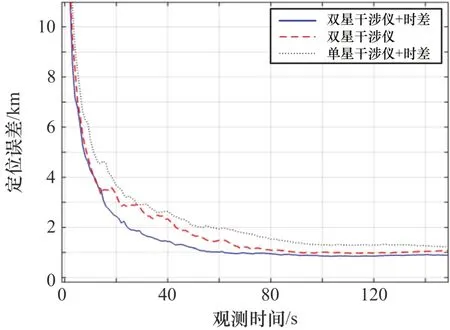
图6 基于时间节拍EKF定位误差

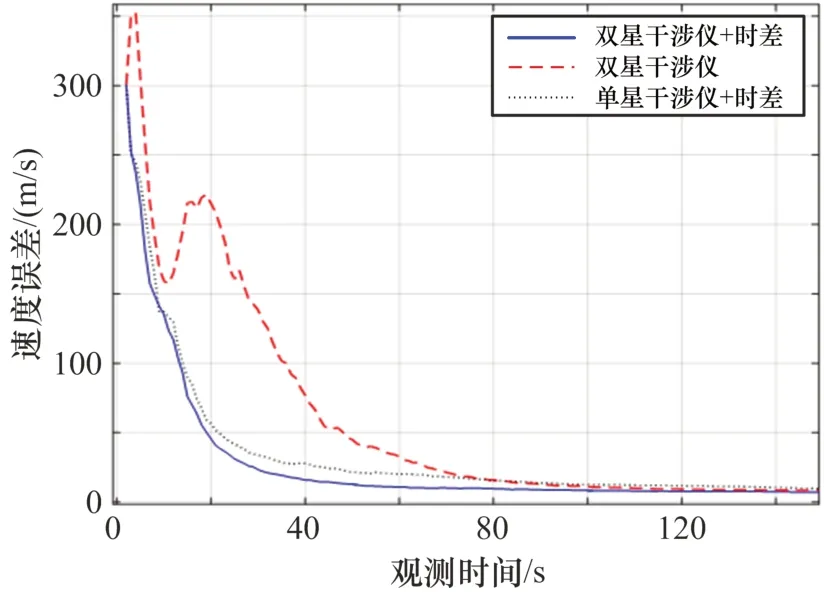
图7 基于时间节拍EKF速度误差

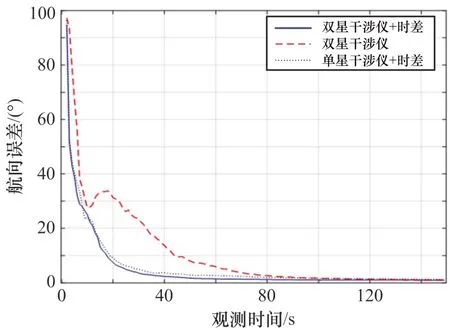
图8 基于时间节拍EKF航向误差

3种观测量的仿真结果比较与基于单脉冲测量数据直接EKF的结论基本一致，采用双星干涉仪相位差+时差作为观测量的滤波方法相比另外2种观测量方法具有更高的目标位置估计精度和更短的速度、航向收敛时间，但收敛后的位置、速度和航向误差均高于基于单脉冲测量数据直接EKF的方法。

3）2种处理流程的仿真结果比较

针对观测量采用双星干涉仪相位差+时差的EKF滤波方法，对单脉冲测量数据直接EKF和基于时间节拍参数估计EKF 2种处理流程的定位误差仿真结果进行比较，如图9所示，其中时间节拍设置了0.1 s、1 s 2种情况。

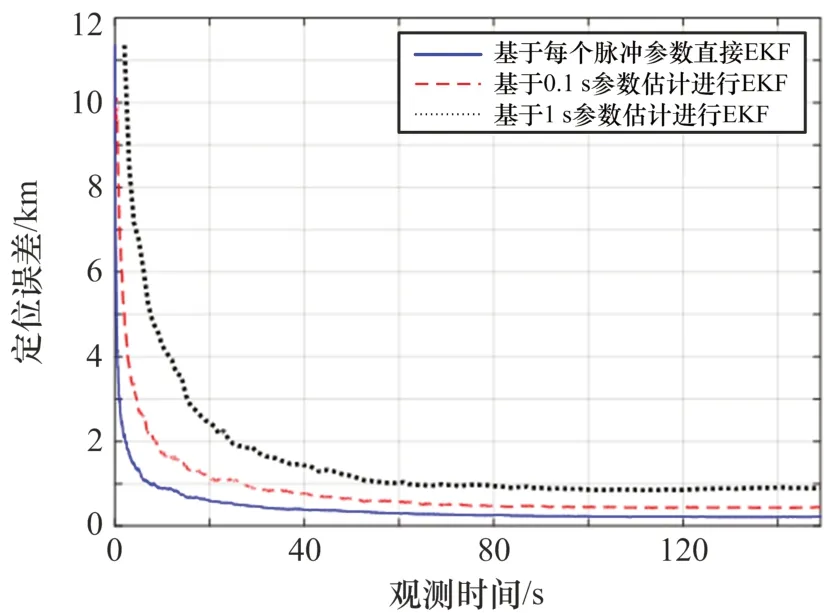
图9 单脉冲EKF及不同时间节拍EKF定位误差比较

从仿真结果可以看出，基于时间节拍参数估计的EKF处理方法在目标位置估计精度和收敛速度方面均低于基于单脉冲测量数据直接EKF的方法，且随着时间节拍增大，估计精度下降明显。原因在于，一是按时间节拍进行相位差和时差参数估计后，损失了相位差变化率和时差变化率等信息；二是用于时间节拍内参数估计的最小二乘估计方法并非最优估计方法，导致滤波过程中引入新的误差。

虽然基于时间节拍参数估计的EKF处理方法在目标位置、速度等状态估计精度上偏低，但其在计算量上相对于基于单脉冲测量数据直接EKF处理方法有明显优势，适合应用于处理资源受限的场景。

5 结束语

本文针对均具备二维正交干涉仪测向的2颗卫星对空中辐射源定位跟踪问题，提出了一种基于干涉仪相位差和时差融合的跟踪滤波方法。首先，从辐射源信号参数原始观测量出发，提出了2种定位跟踪处理流程；其次，在WGS-84坐标系下建立了由时差和相位差构成的观测方程，并采用EKF方法进行跟踪滤波。仿真结果表明，本文提出的目标跟踪方法能够实现未知高程空中运动目标位置、航速和航向的高精度估计，相对于已有方法在收敛速度和估计精度上有明显提高。基于本文的仿真分析结论，在处理资源充分的情况下，采用基于辐射源单脉冲测量数据直接EKF滤波方法能够得到更高的空中目标定位跟踪精度。