一种基于开放气室的土壤呼吸监测装置
谷恪忱,姜俊杰,潘辰昕,孙麒淞,尹文杰,胡军国
(浙江农林大学 数学与计算机科学学院,浙江 杭州 311300)
土壤呼吸是指土壤中的植物根系、动物,以及微生物通过呼吸作用分解有机质产生CO2的过程,其速率反映了土壤生产CO2的速度。作为全球碳循环的重要部分,每年由土壤呼吸释放的碳比化石燃料燃烧释放的碳高一个数量级[1-2],这部分释放的碳主要以CO2气体的形式进入大气。气态CO2作为温室气体的组分之一,对全球变暖的贡献率达到80%[3];因此,土壤呼吸排放碳量的微弱改变都会影响大气中的CO2浓度,潜在地影响全球气候,研究准确测量土壤呼吸速率的方法对预估全球气候变化具有重大价值。
土壤呼吸速率一般难以在野外通过原位测定获得,大部分的土壤呼吸速率通常以土壤表面的CO2通量近似表征[4-5]。目前,测量土壤CO2通量的方法主要有涡度相关法、气井法与气室法[6]。涡度相关法属于微气象学方法,其原理是通过测量近地边界层垂直方向上的风速脉动与CO2气体浓度脉动的协方差计算大范围区域的CO2通量[7],对于湍流发展不充分、地形不平坦的情况,该方法存在较大误差。基于扩散是土壤中CO2气体的主要运输机制,气井法将传感器埋入土壤,通过获得土壤不同深度剖面间的CO2浓度梯度与扩散系数,结合菲克(Fick)定律测算CO2通量;但土壤中CO2气体的扩散系数受土壤孔隙率、含水量影响较大,存在不确定性[8]。气室法是最常用的土壤CO2通量测量方法[4,9],按照其计算原理,可具体分为密闭气室法和动态气室法[10]。
密闭气室法主要通过测量气室内部CO2浓度随单位时间的变化推算土壤CO2通量,测量时气室封闭,土壤表面与外界大气完全隔绝。早期的密闭气室多基于静态的碱吸收原理展开,但由于碱吸收饱和后的测量存在较大的误差,如今已不再被建议使用[11]。当今,大部分的密闭气室采用红外气体分析仪(infrared gas analyzer, IRGA)对CO2浓度进行动态监测,测量的准确性大幅提升。目前,世界上已成功研发出多款集成设备,比较著名的有LI-8100开路式土壤碳通量测量系统(美国LI-COR Biosciences)[12]。然而,由于CO2气体在气室内不断聚集,土壤与大气间的CO2浓度梯度被抑制,因此上述设备无法避免长时间连续测量时的CO2通量低估问题[2]。
开放气室法的测定原理是控制外部补偿气体以一定流量通过气室,待气室内CO2浓度几乎不变,达到准稳态后,测量气室出气口与进气口之间的CO2浓度差,计算CO2通量。典型的开放气室通过气泵将气室内部气体取样至气室外单独的IRGA进行浓度分析。当需要频繁更换监测地点时,这种测量方式缺乏便携性。另外,当补偿气体的CO2浓度非恒定时,出气口处的CO2浓度变化会滞后于进气口处的CO2浓度[13],泵送取样分析会增加额外的时间延迟,若不进行时间校准,会增大CO2通量测量的误差。鉴于传统开放气室的上述不足,研究如何在气室内部直接布置传感器测量CO2浓度是必要的。
近年来,一种商用非色散红外(non-dispersive infrared, NDIR)传感器模块开始被应用于原位CO2浓度的持续测定[14],该传感器模块小巧轻便,相较于传统的IRGA成本低廉,用途广泛。Curcoll等[15]在世界上首次将NDIR传感器安装于开放气室内部,并提出使用该传感器的校准流程。其设计的气室内部加装有风扇,可将土壤呼吸释放的CO2与补偿气体快速地充分混合,以实时监测CO2通量;但与此同时,风扇也会在气室内部引起湍流,从而对土壤表面CO2的扩散产生影响,并且可能改变土壤表面的气压[9],使得通量测算的误差来源更加复杂。因此,关于风扇使用对开放气室测量的影响还需要进一步探究。为避免加装风扇对CO2通量监测带来的潜在影响,本研究设计一套土壤呼吸监测装置(soil respiration monitoring equipment, SRME),借助计算流体力学分析,在不使用风扇的情况下,安装低成本的NDIR传感器至气室内部合适位置,替代IRGA测量CO2浓度,并对补偿气体CO2浓度不稳定情况下测得的CO2通量值进行修正,以实现对土壤呼吸速率的准确测量,进一步提升开放气室的实用性与便携性。
1 材料与方法
1.1 装置设计
监测装置按构造和分工协作原理可划分为控制、气室、底座3大部分。
控制部分主要由NDIR传感器、气泵、流量计、压差计组成(图1)。NDIR传感器型号为K30模块(瑞典Senseair),长58 mm,宽51 mm,厚12 mm,读数量程0~5 000 μm3·m-3,精度为读数的±3%。本研究对K30模块进行定制,使其可以同时监测气温与气压,量程分别为-20~60 ℃和30~110 kPa,精度分别为±0.5 ℃和±0.22 kPa。ZG10-80型气泵(杭州迪凯电子城定制改装)为抽打两用泵,可调控流量为0~10 L·min-1。1179A型流量计(美国MKS Instruments)的量程为0~10 L·min-1,精度是满量程的±0.2%。HCS-3051型压差计(青岛华诚测控设备有限公司)基于单晶硅技术研制,调控量程为-100~100 Pa,精度为量程的±0.075%。本研究用压差计监测气室内外压差,根据压差变化判断流量计是否由于零点迁移而产生流量偏差,以便调控纠正。
气室部分是一个高0.3 m、直径0.3 m、底部敞开的不锈钢圆柱形气室。分别于距离气室底部0.075、0.150、0.225 m处安装直径0.01 m的钢制气管。其中,0.225 m处的两气管分别被设为进气口和出气口,其余气管用作备用管,必要时通过PVC软管与控制部分的压差计相连,不与压差计相连时使用橡胶塞完全密封,以防止气室内部气体泄漏。气室顶部安装有4个电缆接头(图1中仅画出2个),便于传感器与气室外部接线。气室内部有一L形挡板(挡板的具体尺寸如图1所示)将气室划分为进气区与出气区。进气区的作用是充当补偿气体的缓冲区,减小进入气室内部的CO2浓度波动;出气区中的气体与土壤呼吸排放的CO2充分混合,NDIR传感器布置在该区域的合适位置。
底座部分为一高0.05 m、底部中空的环刀底座,其中包括0.02 m高的凹槽,凹槽外径0.310 m、内径0.295 m,用于与气室相嵌,倒入水形成封闭,防止测量过程中CO2外溢。
图2为一种典型的开放气室的仪器布置[16],本研究设计的土壤呼吸监测装置略去了将气室内CO2取样至IRGA的过程,布置测量时更加便利。图3为本研究土壤呼吸监测装置的实物图,其中(a)图展示了气室外部连接状况,(b)图展示了气室内部的挡板和NDIR传感器。
1.2 测算原理
开放气室中的气体变化关系可用质量守恒定律推导[17]。本研究中,气室内部的CO2存在如下守恒关系[18]:
dM=VdCa(t)=A·J(t)·dt+QCi(t)dt-QCo(t)dt。
(1)
式(1)中:dM为气室中CO2气体物质的量的变化,μmol;V为气室体积,m3;A是气室与土壤接触的面积,m2;Ca(t)是气室内空间的平均CO2浓度,μmol·m-3;J(t)是土壤表面的CO2通量,μmol·m-2·s-1;Q为气体流量,m3·s-1;Ci(t)为进气口处的CO2浓度,μmol·m-3;Co(t)为出气口处的CO2浓度,μmol·m-3;t为时间,s。控制进气口和出气口流量都为Q的原因是,使气室内外压差平衡,以避免土壤中产生额外的气体对流[9],从而引起测量误差。
当气室在稳态状况下测量时,气体流量Q、进气口CO2浓度Ci(t)=Ci,出气口CO2浓度Co(t)=Co,均为恒定值,土壤表面的CO2通量Js可用下式计算[19]:
(2)
然而,在实际情况下,由于环境因子变化和仪器误差的限制,式(2)所要求的理想条件难以满足,需要进行修正处理。本研究使用近地边界层的空气作为开放气室的补偿气体,因此考虑如下修正情况:第一,大气的湍流运动致使补偿气体中的CO2浓度产生波动现象,无法保持恒定,影响实际的CO2通量测算值;第二,近地表植物光合作用强度的改变会使每日内近地边界层空气的CO2浓度呈现有规律的缓慢下降和上升变化趋势,而出气口的CO2浓度Co(t)变化与进气口的CO2浓度Ci(t)变化存在时间差,浓度变化的不一致使得CO2通量测算存在误差。
针对第一种情况,结合涡度相关方法中的雷诺时均思想[20],对测量的CO2浓度做时间平均处理,减轻CO2浓度波动的影响:
(3)
式(3)中:变量顶部的上划线“—”指代变量经过雷诺时均处理;Δt表示需要做平均处理的时间间隔,本研究统一取Δt=60 s。
针对第二种情况,由式(1)可推知出气口CO2浓度滞后于进气口CO2浓度变化的时间tc(s)大致如下:
(4)
式(4)中:ΔC为一段时间内进气口处CO2浓度的变化量,μmol·m-3;Jm表示修正前开放气室测得的CO2通量,μmol·m-2·s-1;V1表示使出气口浓度Co(t)发生改变所需的最小体积,m3,该体积具体由出气口的空间位置决定,使用传感器读数时,则相应地与传感器布置的位置有关。对于本研究设计的气室,若出气区NDIR传感器距离气室底面的高度为h(m),气室高为H(m),则近似有
(5)
设进气区与出气区NDIR传感器的CO2体积分数读数分别为cmi(t)和cmo(t),于是根据上述分析,将CO2体积分数换算为体积浓度,本研究中开放气室测算的土壤呼吸速率Rs(μmol·m-2·s-1)将由下式决定:
(6)
式(6)中:Jc表示经过修正的土壤表面CO2通量,μmol·m-2·s-1,具体修正操作视实际测量情况酌情进行,不修正时,式(6)可简化为形如式(2)的公式;Vm为标准气体摩尔体积,L·mol-1;T0为标准开氏温度,K;T为实际开氏温度,K;P0为标准大气压,Pa;P为实际大气压,Pa;T和P由定制的NDIR传感器测得。
1.3 准稳态时间判断
在实际测量过程中,需要大致判断开放气室内部CO2浓度达到准稳态的时间,以便用最少的时间获得准确结果。理论上,可由开放气室内的平均CO2浓度变化判断气室是否达到准稳态。根据文献[18],本研究中开放气室内的平均CO2浓度可由下式决定:
(7)
式(7)中:Dc为CO2气体的扩散系数,m2·s-1;d为土壤-空气界面的静滞空气层厚度,m;Cs为初始时刻土壤表面的CO2浓度,μmol·m-3;Ca为初始时刻气室内的平均CO2浓度,μmol·m-3;取2/3的气室体积(V)是由于L形挡板的阻隔,气室内部实际与土壤释放CO2气体的混合部分仅为出气区,大致占气室总体积的2/3。
当e-(Q/A+Dc/d)/(2/3V/A)·t≤10-3时,可认为气室内的CO2浓度达到准稳态。本研究按文献[18]取d为0.005 m,Dc按标准大气压和标准开氏温度情况取值,Cs和Ca按文献[21]分别取体积分数为450 μm3·m-3和380 μm3·m-3对应的CO2浓度。
1.4 仿真方法
本研究使用Ansys Fluent 2020 R2流体仿真软件获得通气情况下气室内部的CO2浓度场。仿真过程中,关于气体流动的三维稳态连续性方程、动量守恒方程和组分输运方程分别如下[22-23]:
(8)
(9)
(10)
式(8)~(10)中:ρ表示气体密度,kg·m-3;u是气体的流速,m·s-1;μ是空气的动力黏度,N·s·m-2;p为驱动气体运动的压强,Pa;g为重力加速度,m·s-2;c是组分的气体质量分数,%;D为气体中组分的扩散系数,m2·s-1;x为空间位置,m;下标i和j分别表示三维上的x、y、z方向或气体组分,取值为正整数;撇号“′”表示变量的脉动值,即变量瞬时值与一段时间内的平均值之差[20]。
此外,气体在气室内的流动会受到挡板和壁面的阻挡,仿真选取SST k-ω模型模拟流动过程中可能产生的壁面湍流。该模型考虑了流体在低雷诺数和可压缩情况下的剪切流传播,可用于被墙壁束缚的流动预测,在近壁自由流中有广泛的应用范围和精度。关于该模型的参数说明详见文献[24]。
1.5 仿真设置
仿真使用的气室三维模型如图4所示,由于备用管和电缆接头的体积仅占气室总体积的0.07%,为简化分析,故在模型中略去备用管和电缆接头,仅保留0.225 m高处的进气口、出气口和挡板,环刀底座不参与仿真计算。
根据气室三维模型确定的流体域,划分六面体非结构网格,网格数量约为2×106,平均网格质量为0.938,最低质量为0.474,并预先经过无关性验证,以确保仿真的准确性。挡板区域为固体,不参与网格划分与流体计算。具体的网格划分效果如图5所示。
图5 气室网格示意图Fig.5 Diagram of chamber mesh
对划分的每个网格,选择基于压力耦合的Coupled数值算法求解式(8)~式(10),以及SST k-ω湍流模型描述的流体控制方程,该算法对于稳态单相流动的计算更加高效和稳健,非常适合于开放气室内的稳态流场分布的模拟。流体域的压力、动量,及空气各组分气体采用二阶迎风格式离散,其余变量采用一阶迎风格式。
气室的初始条件考虑N2、O2、CO2、H2O为仿真空气的组分气体,根据文献[25]设置前述各组分气体的体积分数分别为79.01%、20.95%、0.038%、0.002%,并令气体温度T为标准开氏温度273.5 K,气压P为标准大气压1.01×105Pa。气室内气体的初始速度、湍动能等其余参数默认为0。
边界条件包括进气口、出气口,及气室底部、土壤接触部分和气室壁面的设置。其中,进气口设为Fluent软件提供的质量入口边界,出气口设为质量出口边界,气室底部设为自由出流边界,气室的壁面边界由Fluent软件自动生成,保持默认。进气口和出气口气体的组分、温度、气压设置同前述初始条件,保持恒定,并分别选取3、4、5 L·min-1的流量验证气室内的CO2浓度分布。
为了使仿真更加接近真实情况,划分距气室模型底部1 cm高的流体域网格为多孔介质区,并通过设置孔隙率和渗透率模拟不同质地的土壤,土壤呼吸速率的模拟可在多孔介质区开启CO2源项实现[26]。由于土壤的孔隙率与气体渗透率在0.25~0.60 m3·m-3[27]和10-8~10-16m2[28]范围变动,故针对3种多孔介质(依次命名为多孔介质1~3)设定不同的孔隙率和渗透率(表1)参与仿真计算。
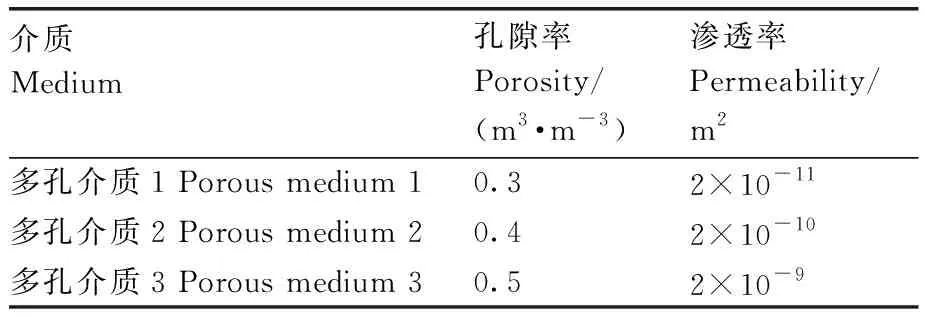
表1 三种多孔介质的孔隙率和渗透率
相应地,土壤呼吸速率在0~16 μmol·m-2·s-1[29],将多孔介质区模拟的CO2源项值依次设为0.5、2、5、10 μmol·m-2·s-1,以模拟不同强度的土壤呼吸速率。
综上,本研究的仿真由3种流量、3种多孔介质、4种土壤呼吸速率相互组合的36个算例组成,每个算例至少数值迭代200次,确保完全收敛。
1.6 传感器布点算法
气室内NDIR传感器布点的位置需要根据36个算例仿真获得的气室内CO2浓度场数据进行分析。为便于叙述,以气室模型底面的圆心为原点,建立三维笛卡尔坐标系(图5),取法向垂直于进气口侧截面的方向为x轴方向,法向垂直于出气口横截面的方向为y轴正方向,法向垂直于气室底面的方向为z轴正方向,单位为m。
从Fluent软件导出36个算例中气室内所有坐标点的稳态CO2体积分数,设置坐标点(0,-0.075,0.225)(单位为m)为进气区NDIR传感器的布点位置,由式(6)计算浓度场内其余各坐标点与该点差分后决定的CO2通量。鉴于近气室底部的气体CO2浓度可能未混合充分,因此筛选出气区z≥0.1 m且CO2通量值与土壤呼吸速率误差小于0.01%的所有点,将所求数据集记为U。
结合k-means聚类算法[30],将数据集U划分为不同簇,取数据样点最多的簇的质心坐标为出气区NDIR传感器的布点位置。簇的个数k由肘部法确定,以欧式距离为度量。
1.7 实地实验
实验选取美国LI-COR公司生产的LI-8100开路式土壤碳通量测量系统(以下简记为LI-8100)和研究团队自制的密闭气室(self-made closed chamber, SMCC)作为标准进行测试对比,两者的测算原理均基于体积分数随时间变化的线性或指数拟合,详见文献[31-32]。SMCC的准确性由团队研发的土壤呼吸校准仪验证[33]。经室内测试,LI-8100与校准仪设置的标准CO2通量值的平均误差约为9%,SMCC约为15%,因此选取SMCC作为LI-8100的替代进行对比是可靠的。
研究区域位于浙江农林大学林业智能监测与信息技术研究重点实验室野外基地,分别在2022-03-15、2022-04-19、2022-04-20、2022-04-21、2022-07-07、2022-07-09选取多处表土草数量较稀疏的测量点进行实地测试。实验时间涵盖全天候(11:00—24:00),对于每个测量点,设置不同的流量(3、4、5 L·min-1)进行测试,每种流量至少测量1次,根据1.3节的准稳态时间判断准则,3种流量对应的准稳态时间大致分别为30、23、19 min,因此每次连续测量都至少持续30 min,以确保装置内的CO2体积分数可以达到准稳态,保证监测的准确性。取测量结束前1 min内使用式(6)计算的所有CO2通量均值作为装置的土壤呼吸速率测量值与标准值进行比较。作为对照,采取空间同质的对比策略,即在本装置测量结束后迅速移除开放气室,在同一位置换上LI-8100或SMCC进行监测。鉴于密闭气室具有只能在短时间进行测量的缺陷,因此至少测量2次,每次测量至少2 min,将多次测量的CO2通量取平均值作为用于对比的标准土壤呼吸速率值。
2 结果与分析
2.1 CO2体积分数场分布
当气室内的CO2体积分数场达到稳态时,进气区的CO2体积分数应与补偿气体保持一致,出气区的CO2体积分数则因与土壤呼吸释放的CO2混合,呈现出明显的梯度分布。在4种土壤呼吸速率情况下,从流量为3 L·min-1,多孔介质孔隙率为0.3 m3·m-3,渗透率为2×10-11m2时的气室yz截面CO2体积分数分布云图(图6)可以看出,由于在多孔介质区设置产生CO2,气室底部的CO2体积分数整体明显高于气室内的其他区域,且在出气区靠近出气口的顶部区域,CO2体积分数整体分布均匀,证明混合效果良好。其余算例的CO2浓度分布状况与此类似,限于篇幅,不再给出。
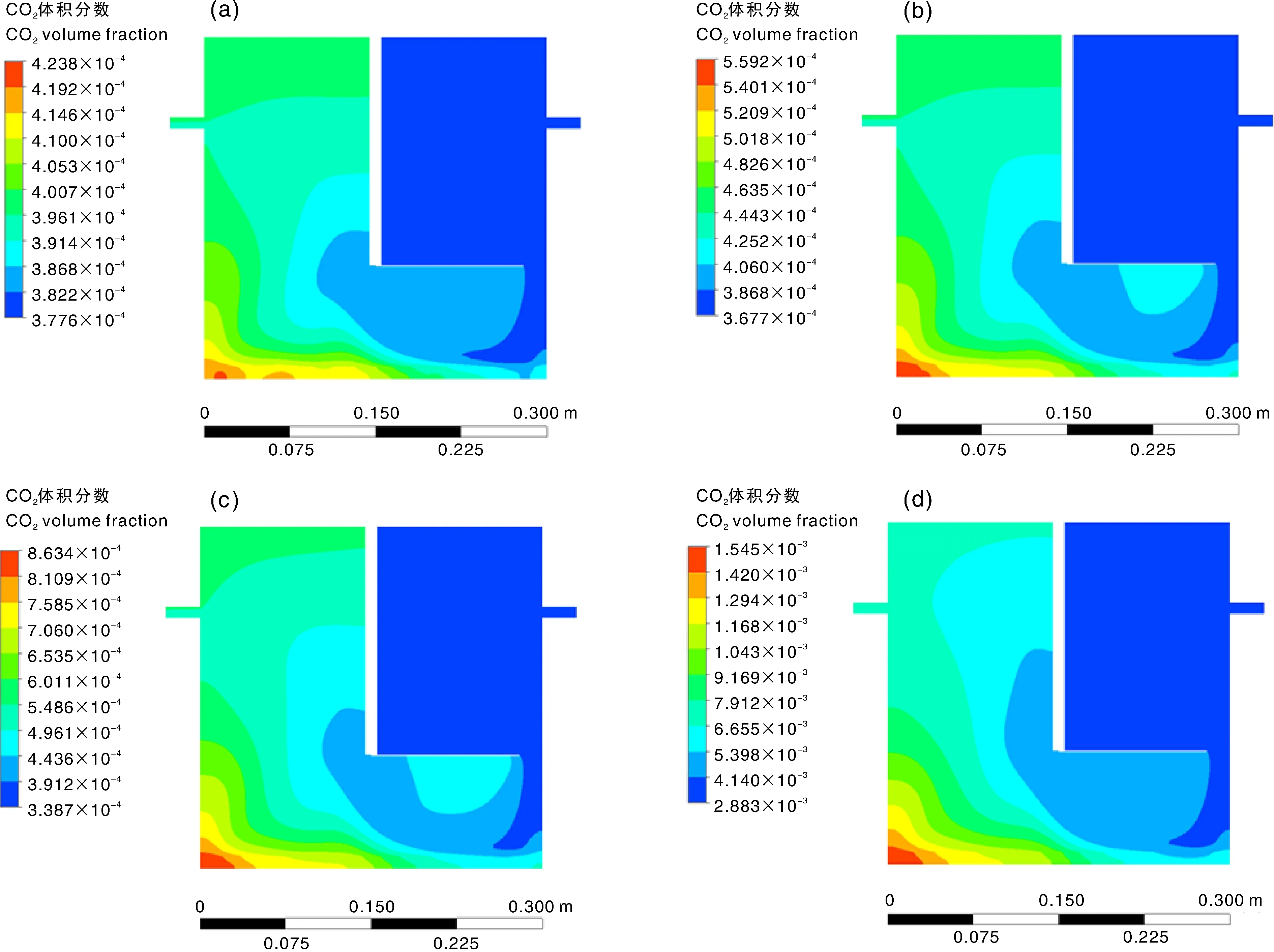
a~d图对应的土壤呼吸速率依次为0.5、2、5、10 μmol·m-2·s-1。The soil respiration rates in a-d are 0.5, 2, 5, 10 μmol·m-2·s-1, respectively.图6 不同土壤呼吸速率下气室内的CO2体积分数廓线Fig.6 CO2 volume fraction contours within chamber at different soil respiration rates
2.2 传感器布点位置分析
36个仿真算例共导出约100万个坐标点数据,经过筛选,得到符合要求的4 091个坐标点,构成数据集U。在应用k-means算法聚类分析之前,首先利用肘部法确定簇个数k值。从簇内点的误差平方和与k值的关系(图7)可以看出,当k值大于5后,簇内误差平方和的下降趋势趋于平缓,因此本研究取k=5进行聚类划分。
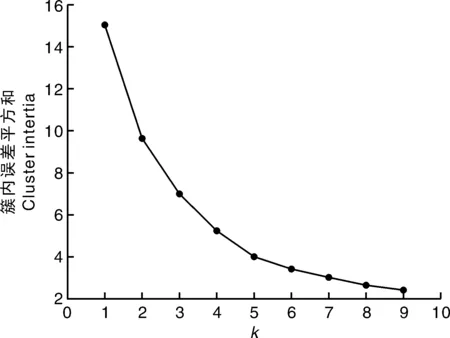
图7 k值与簇内误差平方和的关系曲线Fig.7 Relationship between k value and cluster intertia
使用k-menas算法将数据集U划分为1~5号簇(图8)。将各簇的质心坐标与样本点数量整理于表2,5号簇的样本点数量最多,选择5号簇的质心坐标(-0.046 5, 0.071 7, 0.209 0)(单位为m)为出气区NDIR传感器的理想布置位置。由于NDIR传感器模块的长、宽大致为0.05 m,因此认为以质心坐标为球心、直径0.05 m的球形区域内都是合理的传感器布置范围。取36个算例CO2浓度场中所有该球形区域内的样点,使用式(6)计算CO2通量,发现与实际设置的土壤呼吸速率的平均误差为8.3%。

表2 各簇的质心坐标与样本点数量
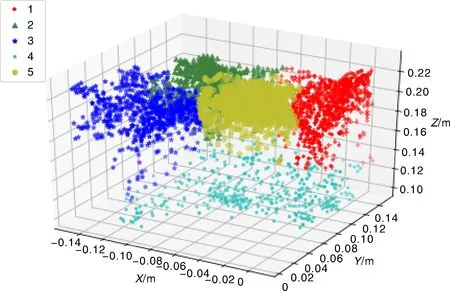
图8 聚类结果Fig.8 Clustering results
2.3 实地测试结果
将NDIR传感器布置至2.2节所述的布点区域,本研究共进行了31次实地测验,其中与LI-8100对比16次,与SMCC对比15次。2022-03-15、2022-07-07、2022-07-09的标准值结果由LI-8100测得,2022-04-19—2022-04-21的标准值结果由SMCC测得(表3),将2022-03-15本研究设计装置(SRME)与LI-8100测得的实际土壤CO2通量测量情况绘制于图9。本装置测量的所有CO2通量均由式(6)计算而得。每次测量时,本装置测得的CO2通量曲线有3个阶段:第一阶段,气室内CO2体积分数未达到准稳态,CO2通量随气室内CO2体积分数快速上升;第二阶段,气室内CO2体积分数达到准稳态,CO2通量动态波动;第三阶段,测量结束,气室被移除后内部的CO2体积分数快速恢复至与空气一致,CO2通量迅速下降。所有测算的土壤呼吸速率值都是在第二阶段准稳态情况下获得的。其余实验日期的CO2通量时间序列与图9类似,限于篇幅不再给出。根据每日测量样本数据的平均值和标准差,可判断本研究设计装置的准确性和稳定性。本研究设计装置的测量结果与LI-8100、SMCC的误差在10%左右,准确性较高,但稳定性较LI-8100和SMCC偏弱,可能与气泵和流量计导致的流量误差有关。
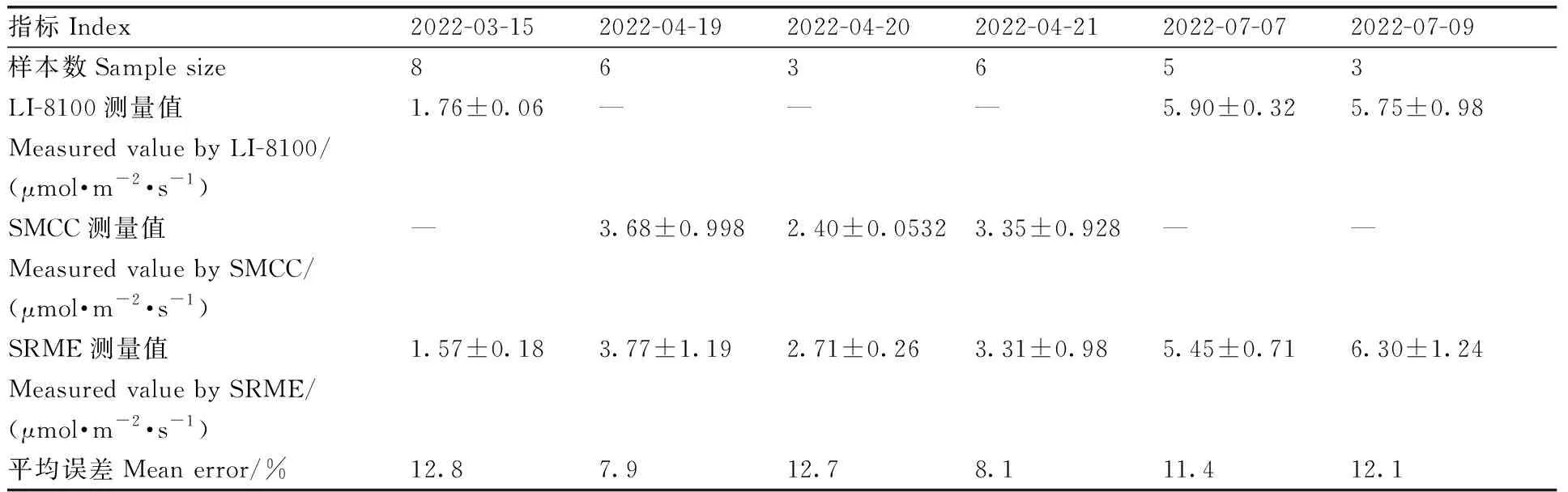
表3 土壤呼吸速率测量结果
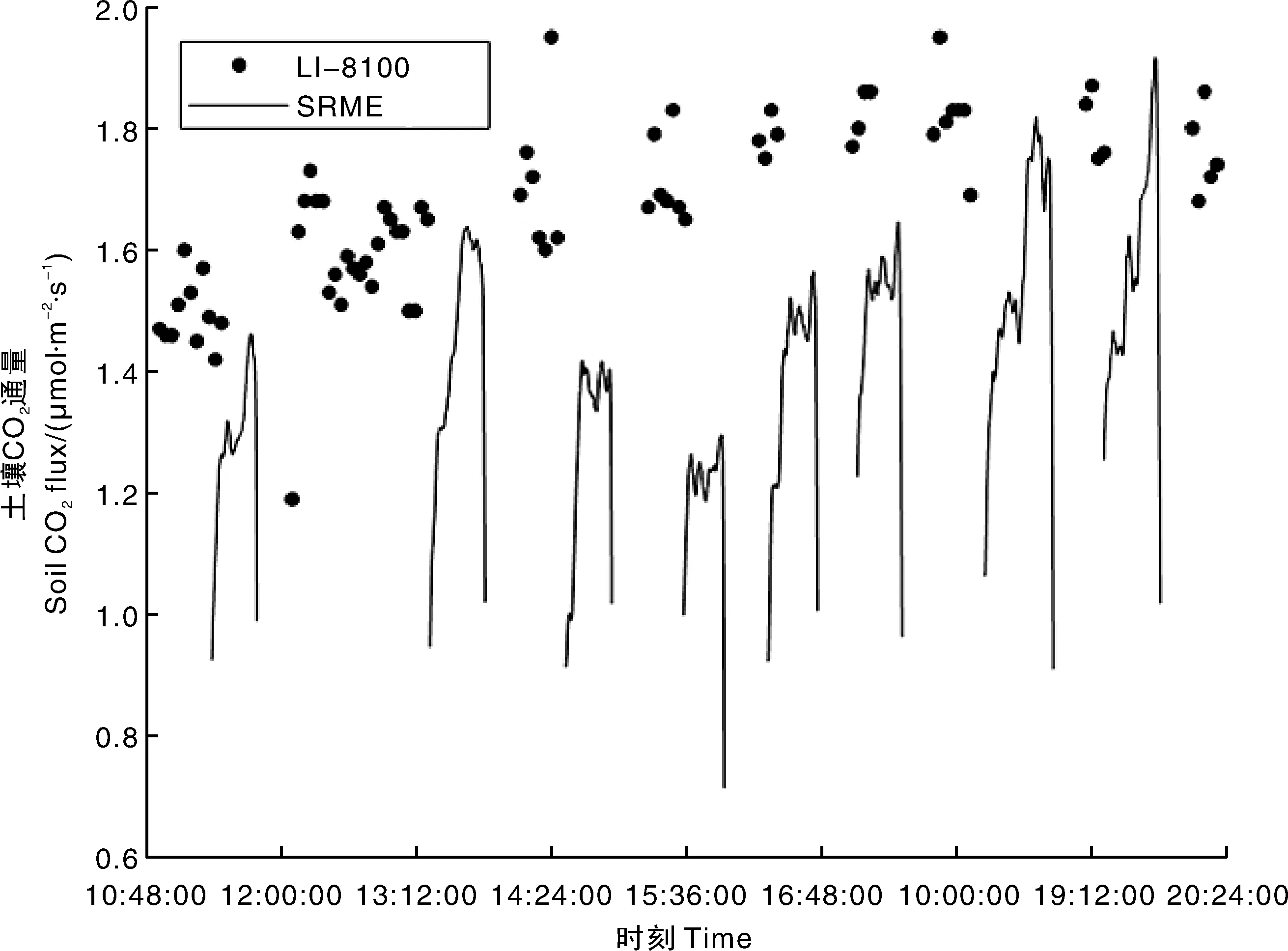
SRME,土壤呼吸监测装置。下同。SRME, Soil respiration monitoring equipment. The same as below.图9 土壤CO2通量时间序列(2022年3月15日)Fig.9 Time series of measured soil CO2 flux (March 15, 2022)
对实验结果进行一元线性回归分析(图10)。以LI-8100、SMCC的测量结果为自变量,本研究设计装置的测量结果为因变量,拟合的直线为y=1.013 4x-0.077 3(R2=0.918 4,P<0.05),皮尔逊(Pearson)相关系数为0.958 3,证明两者具有高度的相关性。

图10 土壤呼吸速率测量结果对比Fig.10 Comparison of measured soil respiration rates
经计算,两者的平均相对误差为10.8%,与2.2节仿真分析得出的预期结果接近,从理论和实际验证了将NDIR传感器布置至以点(-0.046 5, 0.071 7, 0.209 0)为球心、直径0.05 m的球形区域内是合理的。
3 讨论
传统开放气室的CO2浓度测量需要将气室内的气体取样至IRGA,这种测量方式在野外缺乏便利性,并且当补偿气体的CO2体积分数非恒定时,出气口的CO2体积分数变化相较于进气口会有更长的延迟时间,从而导致误差。本研究针对上述不足,设计了一种土壤呼吸监测装置,将传感器直接布置于气室内部替代IRGA分析仪。借助计算流体力学仿真分析,求得以气室内坐标点(-0.046 5, 0.071 7, 0.209 0)(单位为m)为球心、直径0.05 m划分的区域是NDIR传感器布置的合适位置,同时,考虑了补偿气体CO2体积分数非恒定时的修正计算方法,成功获得了准确的土壤呼吸测量结果。经实地测验,本研究设计装置测量的土壤呼吸速率与标准值(LI-8100或SMCC测量值)的平均相对误差为10.8%,Pearson相关系数为0.958 3,与仿真分析得出的理论平均相对误差8.3%相符。
在全球气候变暖的严峻形势下,准确地测量土壤呼吸速率是必要的。本研究设计的基于开放气室原理的土壤呼吸监测装置作为扩充,很好地提供了解决方案,使得开放气室更加便携易用。同时,本装置的测量原理还可适用于其他温室气体排放的监测,具有广泛的应用前景。未来,可进一步考虑优化本装置的设计结构,并提升装置的稳定性与自动化水平。

