例析2023 届佛山一模探讨模拟题命制规律

广东省佛山市教育局教学研究室(528000) 钱耀周

在历年的高三备考过程中,除了常规的复习策略外,利用高考模拟试卷进行考试也是重要的复习手段.一套好的模拟试题,不仅要能够反映出学生的复习状态,还要能够为后续的复习备考指明方向.那么如何命制一套高质量的模拟试题呢? 笔者长期参与佛山市模拟试题的命制与审核工作,所命制的试题在周边地区具有一定的影响力.本文以2023 年佛山市普通高中教学质量检测(一)(以下简称佛山一模)中的部分试题为例,谈谈试题的命制过程与思路.

1 充分利用试题情境,体现数学应用

在本套试卷中,命题团队以佛山的一处地标建筑为背景,命制了一道数列相关试题,具体题目如下:

17.佛山新城文化中心是佛山地标性公共文化建筑.在建筑造型上全部都以最简单的方块体作为核心要素,与佛山世纪莲体育中心的圆形莲花造型形成“方”“圆”呼应.坊塔是文化中心的标志性建筑、造型独特、类似一个个方体错位堆叠,总高度153.6 米.坊塔塔楼由底部4 个高度相同的方体组成塔基,支托上部5 个方体,交错叠合成一个外形时尚的塔身结构.底部4 个方体高度均为33.6 米,中间第5 个方体也为33.6 米高,再往上2 个方体均为24 米高,最上面的两个方体均为19.2 米高.

(1)请根据坊塔方体的高度数据,结合所学数列知识,写出一个等差数列的通项公式,该数列以33.6 为首项,并使得24 和19.2 也是该数列的项;

(2) 佛山世纪莲体育中心上层屋盖外径为310 米.根据你得到的等差数列,连续取用该数列前m(m∈N∗)项的值作为方体的高度,在保持最小方体高度为19.2 米的情况下,采用新的堆叠规则,自下而上依次为2a1、3a2、4a3、…、(m+1)am((m+1)am表示高度为am的方体连续堆叠m+1层的总高度),请问新堆叠坊塔的高度是否超过310 米? 并说明理由.

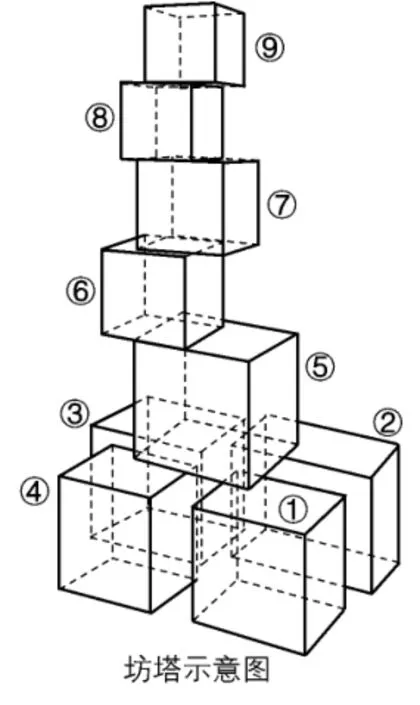
本题的背景新颖,所选地标建筑具有很好的观赏价值,能够很好地提升佛山本土学生的文化自信.

其次,则是试题情境在解题中的应用.在多数情境类试题中,情境与试题较为割裂,去除情境都不影响解题.而本题的情境在解题过程中至关重要,其中部分信息还是通过图形提供的.学生需要识别“坊塔塔楼”的结构来研究每一层的数量,为了降低难度,笔者提供了“示意图”供同学们参考.

最后,则是设问的角度,本题放弃了求通项、求和等常规考查方式.以开放性的问法让学生构建出一个“等差数列”.而该数列并不是完全开放,-2.4、-1.2,-4.8 都可以作为数列的公差,但不同的选择则决定了后续解题的运算量.第(2)问是从设计的视角搭建一个新的“堆叠坊塔”,限于试题的难度,本题仅选择塔高作为判断的依据.若将该题进行拓展,还可从“美观”的角度进行研究.

在试题的命制过程中,命题团队也探讨过数据的运算量问题.是否需要对数据进行“美化”,仅保留整数部分进行设问.例如,在原题干背景下,由某学生社团仿照该建筑制作了一个“坊塔”模型,该模型的数据就可以完全设计为整数.笔者认为,在平时的教学中,为了体现相关的解题思想,我们常常简化数据的运算.但数据运算是现阶段所倡导的数学六大学科核心素养之一,所以命题团队认为有必要提升学生的运算能力.为此,团队特意查询了该建筑的真实数据,本题所采用的数据也均为真实数据.

本题充分地体现了数学的应用价值,考查了学生的直观想象、数据运算、逻辑推理等核心素养.笔者认为,本题为情境类试题的设置提供了很好的范例.

除该试题外,本套试题还有两道情境类试题,现展示如下:

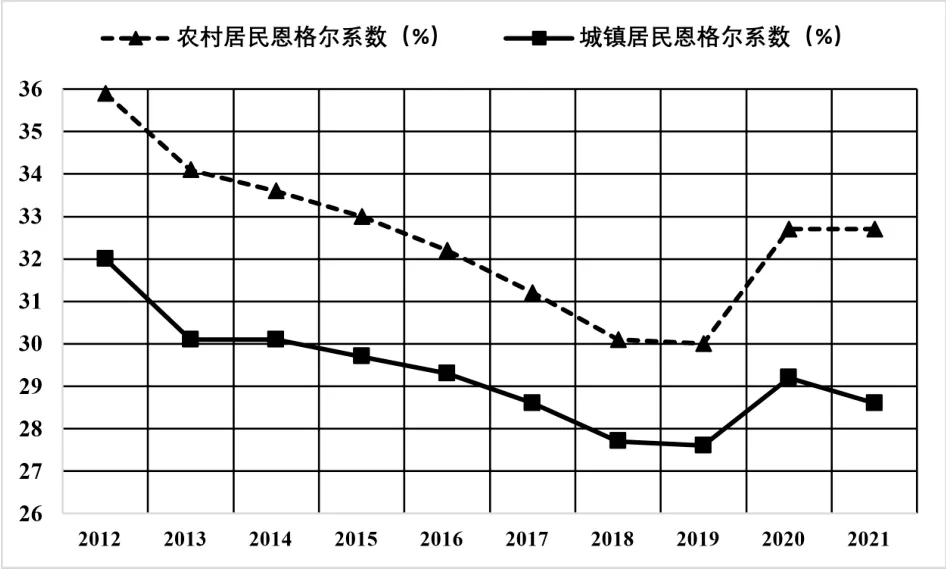
9.中国共产党第二十次全国代表大会的报告中,一组组数据折射出新时代十年的非凡成就,数字的背后是无数的付出,更是开启新征程的希望.二十大首场新闻发布会指出近十年我国居民生活水平进一步提高,其中2017 年全国居民恩格尔系数为29.39%,这是历史上中国恩格尔系数首次跌破30%.恩格尔系数是由德国统计学家恩斯特·恩格尔提出的,计算公式是“恩格尔系数=×100%”.恩格尔系数是国际上通用的衡量居民生活水平高低的一项重要指标,一般随居民家庭收入和生活水平的提高而下降.恩格尔系数达60%以上为贫困,50%∼60%为温饱,40%∼50%为小康,30%∼40%为富裕,低于30%为最富裕.如图是近十年我国农村与城镇居民的恩格尔系数折线图,由图可知( ).

A.城镇居民2015 年开始进入“最富裕”水平

B.农村居民恩格尔系数的平均数低于32%

C.城镇居民恩格尔系数的第45 百分位数高于29%

D.全国居民恩格尔系数等于农村居民恩格尔系数和城镇居民恩格尔系数的平均数

20.近几年,随着生活水平的提高,人们对水果的需求量也随之增加,我市精品水果店大街小巷遍地开花,其中中华猕猴桃的口感甜酸、可口,风味较好,广受消费者的喜爱.在某水果店,某种猕猴桃整盒出售,每盒20 个.已知各盒含0,1个烂果的概率分别为0.8,0.2.

(1)顾客甲任取一盒,随机检查其中4 个猕猴桃,若当中没有烂果,则买下这盒猕猴桃,否则不会购买此种猕猴桃.求甲购买一盒猕猴桃的概率;

(2)顾客乙第1 周网购了一盒这种猕猴桃,若当中没有烂果,则下一周继续网购一盒;若当中有烂果,则隔一周再网购一盒;以此类推,求乙第5 周网购一盒猕猴桃的概率.

第9 题中的“恩格尔系数”是衡量居民生活水平高低的一项重要指标,在人教版教材必修一函数这一章节中,首次提出过该概念.但本题对概念还是进行了说明,降低了试题的难度,将问题转化为阅读信息,理解图表统计量的相关信息.其次,本题还考查了处理数据的能力,例如百分位数的求解还需对图中的数据进行重排,最后通过估算获得.很好地考查了数据运算的核心素养.

第20 题的情境通俗易懂,考查的核心知识在于全概率公式、条件概率等.体现了新教材中新增知识在考试中的考查方式.而且设问方式符合客观规律,体现了数学应用价值.其次,本题也可从商家的视角出发,根据烂果率决策备货的数量,由此改编成一道决策类试题.

2 重视新、旧教材变化,突出新增内容

与旧教材相比,新教材有很大的变化.包括知识的顺序,增减的知识点等等.除在上文中提到的全概率公式外,“投影向量”也是一个新的概念.

18.在锐角三角形∆ABC中,角A,B,C的对边分别为a,b,c,为在方向上的投影向量,且满足

(1)求cosC的值;

(2)若b=a=3ccosB,求∆ABC的周长.

在旧教材中,我们只学习了“投影”的概念,“投影”是一个数量,其本质是为了构建向量的数量积.而投影向量是一个新的向量,体现了向量的运算过程.本题对“投影向量”的考查方式较为直接,需要考生明确概念,并将其与图形相结合发现∆ABC边、角间的关系.

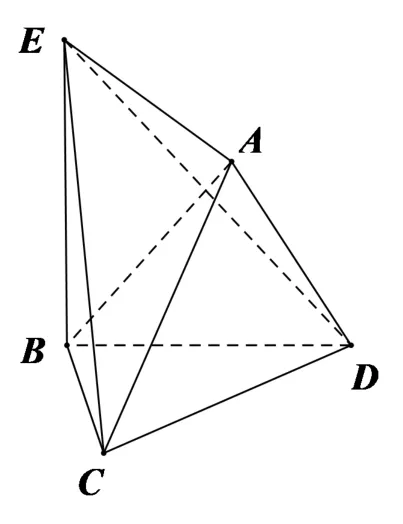
19.如图,∆ACD和∆BCD都是边长为2 的等边三角形,平面ACD⊥平面BCD,EB⊥平面BCD.

(1)证明:EB//平面ACD;

(2)若点E到平面ABC的距离为求平面ECD与平面BCD夹角的正切值.

本题的第2 问考查点到平面的距离,常规方法是利用等体积法将其转化为易求解的几何量进行运算.若从空间向量的视角研究,可通过向量在法向量上的投影来进行运算.所以本题也可理解为“投影向量”在空间图形中的考查与应用.

3 挖掘经典模型,构建新颖试题

作为一套完整的试题,还需要考虑试题的难易搭配,以及亮点题目的设计.其中圆锥曲线试题因为背景丰富,且解题视角多样,常常作为亮点试题精心设计.如何命制此类试题呢? 笔者认为首先要了解此类试题的一般化结论,再根据结论的特点进行改编再创造.现以21 题为例,简介如下:

(1)求椭圆Γ 的方程;

(2)设过F的直线PQ交椭圆Γ 于P,Q两点,若直线PA,QA与直线l:x+4=0 分别交于M,N两点,l与x轴的交点为k,则|MK|·|KN|是否为定值? 若为定值,请求出该定值;若不为定值,请说明理由.

对于圆锥曲线试题,一般都具有普遍的结论.本题的设问方式是考查两个线段间的关系,但本质上是探究直线PA与QA的斜率之间的关系.

两条直线的斜率之积为定值,由此衍生出对应的两条线段之积也为定值.由此可将l更换为其他直线(与x轴垂直)时,对应的线段之积仍为定值.

现将一般化结论介绍如下:

本题在设计该问题时进行了一次包装,将斜率的定值问题转化为线段的乘积之间的关系.这样的设问方式还增加了解题的突破口,为了降低运算方面的难度,本题还选择将点T特殊化为椭圆的左焦点,对应的线段设计为椭圆的左准线,这也是为了突出椭圆的几何特征,由此也可衍生出利用第二定义的相关知识进行求解.

4 命制试卷的核心理念

本次模拟试题的命制过程坚持重基础、重本质、重应用、重创新的一贯命题思路,实现强化了“三位一体”(考查内容、考查要求、考查载体)的认识.命题更加强调了“知识为基、能力为重、素养导向、价值引领”的理念,更加突出考查数学本质,重视理性思维的考查,更加关注学生问题解决能力和学科素养,在关键能力的考查上更加深入.命题时,我们充分吸收党的二十大精神以及新时代对数学人才的要求,多角度思考命题所能起到的引领作用,贯彻德智体美劳全面发展的教育方针,设计真实问题情境,体现我国的社会主义建设成就和社会主义的制度优势,具有鲜明的时代特色,发挥数学试卷的育人价值

笔者认为,模拟试题承载着复习备考的指导作用.本套试题突出新旧教材的差异,倡导数学文化,深入分析经典结论,为后续的复习备考指明了方向.