基于模糊随机森林模型的教育培训系统故障预测方法研究

周青云, 张朝鑫, 郭建龙

(1.广东电网有限责任公司培训与评价中心,广东,广州 510520;2.广州海晟科技有限公司,广东,广州 510520)

0 引言

随着经济的发展和社会生活水平的提高,信息化技术也得到了发展,信息化技术逐渐应用到多个领域。教育领域最典型的应用就是教育培训系统,一旦发生故障便会阻碍教学任务的正常进行[1-2],因此对教育培训系统故障的研究具有重要的意义。目前,有一些专家学者进行了相关研究,部分学者针对教育培训系统的使用过程进行了研究,建立了风险评价指标体系,但是该方法主要是针对使用者的风险考虑较多[3-4]。还有部分学者针对教育培训系统建立了TOPSIS模型评估网络参数影响的重要性,但该方法仅从网络参数的角度出发,并未对参数数据进行深入的运算[5-6]。更有部分学者建立了BP神经网络模型,获取教育培训系统运行过程中的参数,输入到BP神经网络中,输出目前的风险等级,但从实际应用效果中看,BP神经网络对教育培训系统故障预测的准确率仍有待提升[7-8]。因此,本研究从教育培训系统故障预测的角度出发,建立基于模糊随机森林的教育培训系统故障预测模型。通过物联网的无线采集设备获取教育培训系统的运行参数,利用模糊控制算法优化随机森林算法降低重要度较低特征的干扰,将优化后的数据作为随机森林算法的输入,输出风险故障预测信息,提高教育培训系统故障预测的准确率。

1 基于物联网的系统参数感知

按照COWA算子赋权法的计算步骤采用的指标进行计算,得到所有指标的权重值。

1) 将指标Ci的专家评分数据{a1,a2,…,an}重新排列,并从0开始编号得到新评分数据集:

{b0,b1,…,bj,…,bn-1}

(1)

式中,b0≥b1≥…≥bj…≥bn-1。

2) 对得到的新评分数据集进行权重赋值,计算加权向量ωj+1:

(2)

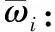
(3)

式中,ωj+1为加权向量,且ωj+1∈[0,1],bj为新评分数据集的各数据。

4) 计算指标Ci的相对权重值ωi:

(4)

式中,i为评价指标数量,i=1,2,…,t。

2 基于模糊随机森林的教育培训系统故障预测模型

模糊控制算法具备较强的抗干扰能力和容错性,它通过语言变量和模糊条件语句等方法,以模糊数学、模糊集合理论、模糊语言和模糊逻辑为基础,将自然语言转换成对应规则,基于这些规则对系统进行控制。随机森林算法是由多颗CART树组成的强学习器,是一种集成学习的方法,通过统计所有弱学习器的输出得到预测结果,对缺失特征不敏感。与其他机器学习算法相比,随机森林算法泛化能力更强、准确率更高。

决策实验室分析(DEMATEL)方法可以有效地解决指标间关联情况不明确的问题,并且通过计算中心度能够得到各指标的关联权重。但是,DEMATEL方法在构建直接影响矩阵时常受到专家评价信息主观性和模糊性的影响,赋权结果缺乏准确性。本文利用三角模糊数(TFN)表达专家语言信息方面的优势,在原DEMATEL方法中增加TFN模糊化—重心法解模糊的处理过程,提高DEMATEL方法的客观性和合理性。

1) TFN模糊化

三角模糊数(TFN)可用Ak(lk,mk,rk)表示,其中lk、mk、rk分别代表模糊数的上限值、可能值、下限值。利用式(5)可计算得到语言变量Sk对应的模糊尺度,并构建三角模糊直接影响矩阵S:

(5)

式中,k为语言变量的数量。

2) 重心法解模糊

利用式(6)进行重心法去模糊化,得到对应的清晰值Pk,并构建清晰直接影响矩阵Q:

(6)

3) 规范化直接影响矩阵G:

(7)

4) 获得综合影响矩阵Z:

(8)

5) 求解中心度Ri和原因度Ti:

Ri=Ei+Fi

(9)

Ti=Ei-Fi

(10)

(11)

(12)

式(9)～式(12)中,Ei和Fi分别为影响度和被影响度,zij为n×n的综合影响矩阵中第i行第j列的数值,i=1,2,…,n,j=1,2,…,n。

6) 获得指标权重μi:

(13)

3 实验结果分析

本文利用基于6LoWPAN的无线传感器网络采集教育培训系统运行参数,一共10组数据。将数据集以6∶4的比例划分为训练集和测试集,并用来验证模糊随机森林算法在教育培训系统故障预测中的效果。

根据图1影响因素提取的运行结果可知,当影响因素数为5时,分类精度最高,所以根据影响因素的权重计算排序,将排名在前5的影响因素进行提取,如图2和表2所示。

表2 原始参数数据

图1 影响因素个数和分类精度之间关系

图2 模糊随机森林模型

通过对模型对比的实现结果可知,基于模糊随机森林的模型教育培训预测效果较高、准确率较高,其余模型的预测准确率与实际结果相比均有一定程度的差异。

4 总结

本文通过对教育培训系统故障问题的研究,建立基于模糊随机森林的教育培训系统故障预测模型,在传统的随机森林方法基础上进行改进。模型可知,基于模糊随机森林的教育培训系统故障预测模型的准确率较好。