电动汽车无线充电高效高利用率磁芯的多目标优化设计 *

熊 萌，张 栋，尤国建，孙添飞，盛 凯，魏学哲

（1. 中国汽车工程研究院股份有限公司，重庆 401120； 2. 同济大学新能源汽车工程中心，上海 201804）

前言

无线传能（wireless power transfer， WPT）技术作为电动汽车前沿充电技术，充电过程无线缆连接，具有快速灵活、方便安全、易维护等优势，是目前行业的研究热点［1-4］，其与自动泊车、自动驾驶、V2G 等技术结合，可实现停车即走、自主充电、电网互动等场景应用［5-7］。但仅通过松耦合线圈无法实现大间隙高效率大功率传输，须在线圈耦合结构中铺设适量高磁导率磁芯，以提升线圈传输性能，并减小磁辐射泄漏。因此，作为核心传能部件，功率铁氧体磁芯被广泛用于电动汽车无线充电领域［8-13］。

由于磁芯结构及排布对无线传能的性能影响较大，国内外以提升系统传输效率并减小磁芯损耗等［14-17］，对磁芯结构的优化设计展开了广泛研究。根据磁芯参数与优化约束复杂度，总结的国内外磁芯结构研究如图1所示。图1（a）中Strauch等［14］将简单的条形磁芯结构呈辐射排布，优化分析了磁芯参数对耦合系数与磁芯体积的影响。相比形状单一的磁芯结构，特殊结构的磁芯可提升优化空间，对磁场调控更科学，如图1（b）中刘志珍等［15］在DD 线圈绕组两空心区域增加磁芯厚度，提出了双凸型磁芯结构，有效提高了线圈耦合磁通量。

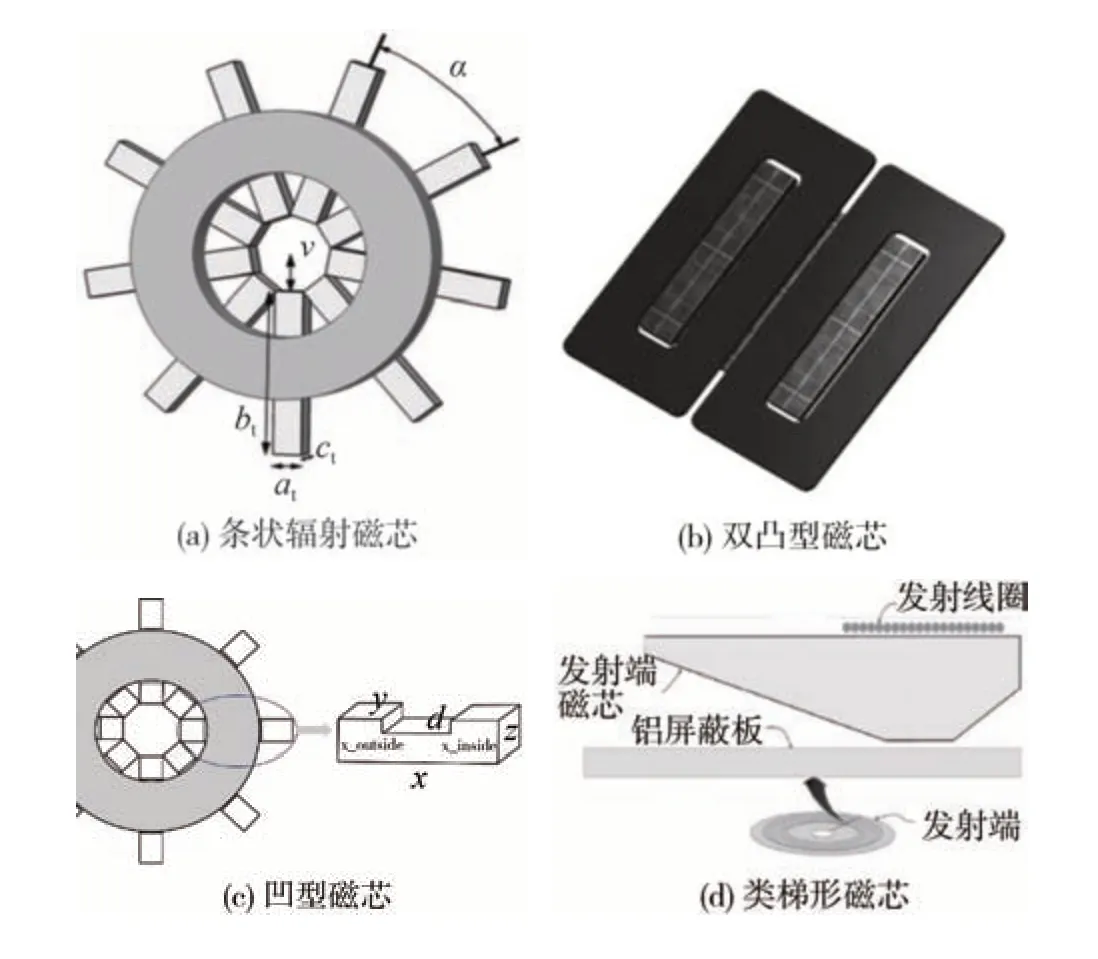
图1 4种国内外的磁芯结构

进一步地，随着无线充电功率等级的提升与产业化推进，对特殊结构磁芯的磁饱和、磁损耗、磁利用率等非线性问题提出了约束，此类研究保证了系统传输性能，最大化提升了磁芯优化空间，为解决磁芯体积小型化与大功率快充需求之间的矛盾提供了思路。图1（c）中孙跃等［16］基于圆形线圈提出了凹型磁芯结构，并考虑磁饱和问题，约束了优化磁芯的最大磁通，优化后凹型磁芯体积减小22%，系统理论输出功率与效率分别提高了37%与10%。上述研究未考虑磁芯磁通分布不均匀的问题，因此Mohammad等［17］提出了图1（d）中类梯形磁芯结构，对磁芯磁通分布的均匀性进行约束，优化后磁芯磁通均匀性显著提高，避免磁饱和的同时，提高了低磁通密度区域的磁芯利用率，降低了磁芯损耗。

综上，简单结构的磁芯优化参数少，优化空间小，适用于对磁芯体积要求不高的低功率无线充电应用。不考虑磁芯非线性特性的特殊磁芯结构的优化设计往往忽略了磁饱和问题，如图1（b）中凸型磁芯结构的中部既是较薄区域也是主磁通区域，因此该区域在大功率下可能出现局部磁饱和问题。虽然上述第4 种磁芯研究考虑了磁饱和与磁利用率问题，但仅从定性角度给出了磁芯磁通分布的调控方向，并未定量给出磁通均匀性与磁损耗之间的关系。

为提升抗偏移性能，电动汽车无线充电的地面发射线圈尺寸往往大于接收线圈，因此发射端磁芯物理尺寸跨度较大，面临更显著的磁通不均匀性与更高的磁损耗问题［18］。针对磁通不均匀性更严重的非对称DD 线圈发射端，本文将基于其等效电路模型与等效磁路模型，提出磁芯磁通均匀性评价指标，建立其与磁芯损耗、磁芯体积的定量关系。据此，提出一种面向11 kW 功率级发射端应用的新型磁芯结构，并进行基于Pareto 前沿的NSGA-II 多目标优化与实验验证，旨在提升磁芯磁通均匀性以减小磁损耗，增大磁芯利用率，并进一步提高线圈间耦合性能，最终解决磁芯在大功率车用无线充电中的小型化高效应用。

1 无线充电系统方案与建模

无线充电系统由作为核心传能部件的磁耦合线圈组、提升传能效率的补偿拓扑以及保证系统稳定传能的控制电路组成，其中线圈类型将直接决定磁芯排布设计，补偿拓扑及控制类型则决定了额定功率下磁芯磁通大小，因此须首先确定本无线充电系统的优化初始方案。

1.1 参考磁耦合线圈组及拓扑方案

相比圆形与方形线圈，DD线圈在较大横向偏移下耦合性能最佳，因而被广泛用于电动汽车无线充电研究［19-20］。同时，一大一小的非对称线圈组耦合磁通更均匀，抗偏移能力更强，已成为车用无线充电的产业标准化方案。本文选取同济大学Luo 等［21］基于最大耦合系数与最小磁泄漏优化所得发射线圈，作为本文优化的初始参考磁耦合线圈，其结构及实物如图2（a）和图2（b）所示，发射端采用直径4 mm的24匝多股利兹线，通过3线并联绕制而成（等效为8 匝），条形铁氧体与铝板分别为10 与4 mm 均匀厚度。接收端则采用SAE J2954 标准［22］中11 kW 功率级与Z2 间隙等级的DD 线圈作为标准接收线圈，如图2（c）和图2（d）采用直径5 mm 的6 匝多股利兹线单线绕制而成，条形铁氧体与铝板分别为8 与3 mm均匀厚度。

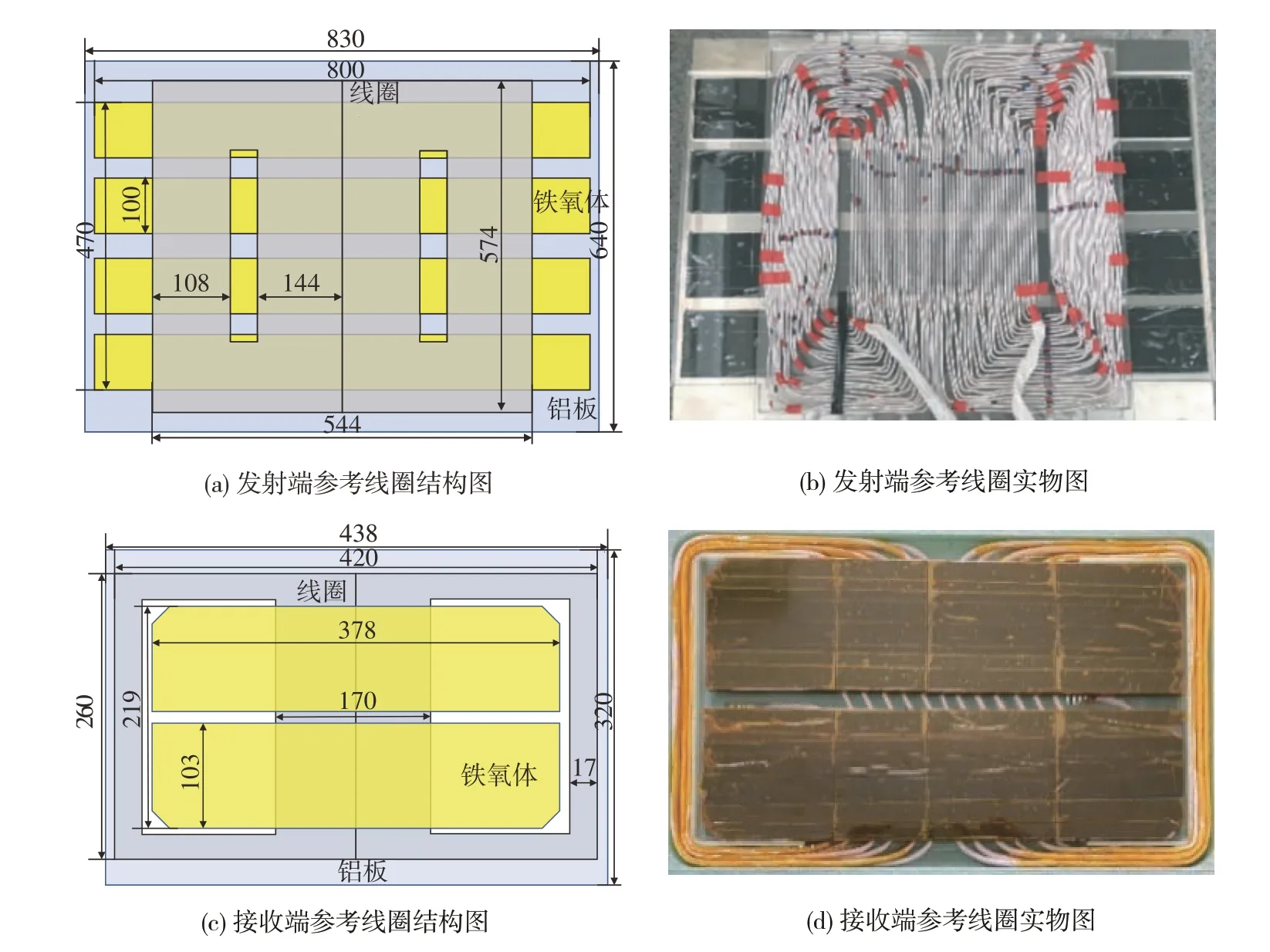
图2 选定的非对称DD参考磁耦合线圈组

单通过松耦合线圈组无法实现系统高效传能，同时为保证优化工作可操作性，选定抗谐波能力强且具有恒流输出特性的LCC-SP 拓扑作为补偿拓扑［23］。在接收端采用具有电流放大作用的倍流整流控制电路，以缓解高功率密度带来的大电流负荷问题，系统结构如图3所示。

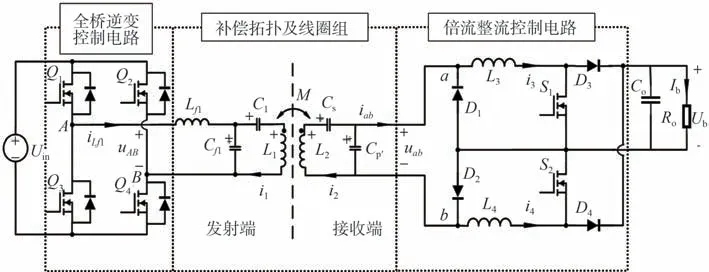
图3 基于LCC-SP拓扑与整流控制的无线充电系统

1.2 磁耦合线圈组等效模型建立

虽然1.1 节中选定的非对称线圈组缓解了耦合衰减与功率波动问题，但过大的发射端结构将导致磁芯磁通分布不均，磁损耗增大。为解决该问题，并进一步提升线圈间耦合系数，本节将针对选定的参考磁耦合线圈组建立其等效电路模型与等效磁路模型，为磁损耗的提取与磁芯结构的排布优化提供理论指导依据。

1.2.1 考虑磁芯损耗的等效电路模型

发射端磁芯损耗作为本文的重要优化指标，须将其从线圈、磁芯、铝板3 大组件损耗中分离。各组件等效电阻可用各自损耗与线圈激励电流的比值表征［24］，如式（1）所示。其中，Rtx_coil、Rtx_core、Rtx_sh分别表示发射端线圈、磁芯、铝板的等效电阻，Itx表示发射线圈的激励电流。上述组件损耗中，发射线圈损耗Ptx_coil来自线圈绕组单独产生的电阻损耗，一旦绕组与工作频率确定，Rtx_coil不随线圈电流值变化。铝板损耗Ptx_sh由铝屏蔽板高电导率产生的感应涡流引起，而感应涡流与线圈中安匝电流成正比，因此铝板损耗可用与绕组串联的铝板交流电阻Rtx_sh表示，可视为恒定值［24］。虽然磁芯损耗也可通过与线圈电流有关的附加串联电阻表示，但由式（2）斯坦梅兹经验公式推导出磁芯等效串联电阻随实际通过的线圈电流呈式（3）的非线性关系，其与磁芯系数β有关［17］。

式中：Pv为单位体积的磁芯损耗，kW/m3；f为工作频率，Hz；Bm为磁通幅值，mT；Cm、β为磁芯系数，与磁芯材质及工况有关。

通过实测单位体积磁芯的P-B损耗曲线，拟合求得85 kHz 工作频率下，本文所用功率铁氧体磁芯的磁芯系数Cm=1.13×10-8，β=2.4，拟合相关度R2=0.992。据此，建立参考DD 线圈组的等效电路模型（见图4），其中VAC为交流输入源，RL为等效负载电阻，Ztx与Zrx为收发端补偿阻抗，L1、L2、M分别为发射线圈自感、接收线圈自感、线圈间互感。线圈电流流过收发端组件电阻，参考发射端的线圈及铝板等效电阻Rtx_coil与Rtx_sh可通过LCR 仪测得，再由实测发射线圈电流求得发射线圈损耗与铝板损耗，最后经发射端总损耗间接剥离得到磁芯损耗。

图4 非对称DD参考磁耦合线圈组的等效电路模型

1.2.2 考虑线圈耦合的等效磁路模型

分析线圈不同位置处磁芯磁阻调控对线圈耦合性能的影响，划分参考线圈组的空间耦合区并建立其等效磁路模型。由磁通连续性定律，DD发射线圈激发的磁通一部分被自身耦合，另一部分被接收线圈耦合。根据XOZ截面磁通的空间分布，如图5 所示划分自耦合区与互耦合区。据此建立对应的等效磁路模型，DD发射线圈两并列矩形线圈产生的磁动势F1与F2可类比为电动势，Rs1、Rs2与Rs3分别为对应自耦合区的空间磁阻，Rm1与Rm2为线圈间互耦区的空间磁阻，Фs1、Фs2与Фs3分别为对应自耦合区的空间磁通，Фm1与Фm2为各互耦区的空间磁通。

图5 参考线圈组的空间耦合划分与等效磁路模型

根据等效磁路模型，得到线圈互耦合磁通Фm与自耦合磁通Фs的表达式为

由于DD 发射线圈两并列串联矩形线圈完全相等，则磁动势F1=F2。结合式（4），推导化简得到参考DD 线圈组的耦合系数k如式（5），各耦合区空间磁阻大小等于该区域磁导Λ的倒数，自耦合区1 与自耦合区2 磁阻并联后的磁导表示为Λ//=1/（Rs1//Rs2）。

综上，若需提升非对称DD 线圈耦合性能，可减小磁导（Λs3+Λ//），增大 （Λm1+0.5Λm2），即减小相应互耦合区的磁阻，增大相应自耦合区的磁阻。因此，通过合理的发射端磁芯排布设计，可实现对线圈等效磁路的磁阻优化。

2 磁芯磁通均匀性问题研究

车用无线充电磁芯存在磁通分布不均的问题，尤其大功率下局部磁通过高将导致磁饱和，局部过低则磁芯未被充分利用，且磁芯磁通是否均匀将直接影响磁芯损耗。为调控发射端磁芯磁通，对发射端磁芯磁通均匀性问题展开研究。用11 kW 实测线圈电流值Itx-RMS=34 A 与Irx-RMS=39 A 激励线圈组仿真模型，得到图6（a）中参考发射端磁芯磁通分布，磁通主要集中在中心区域，而沿X轴两侧边缘附近磁通较低。在三维空间下磁通呈如图6（b）所示的近似正态分布，且沿X截线方向磁通差异较大，Y方向则差异较小，因此须重点调控磁芯X方向磁通。

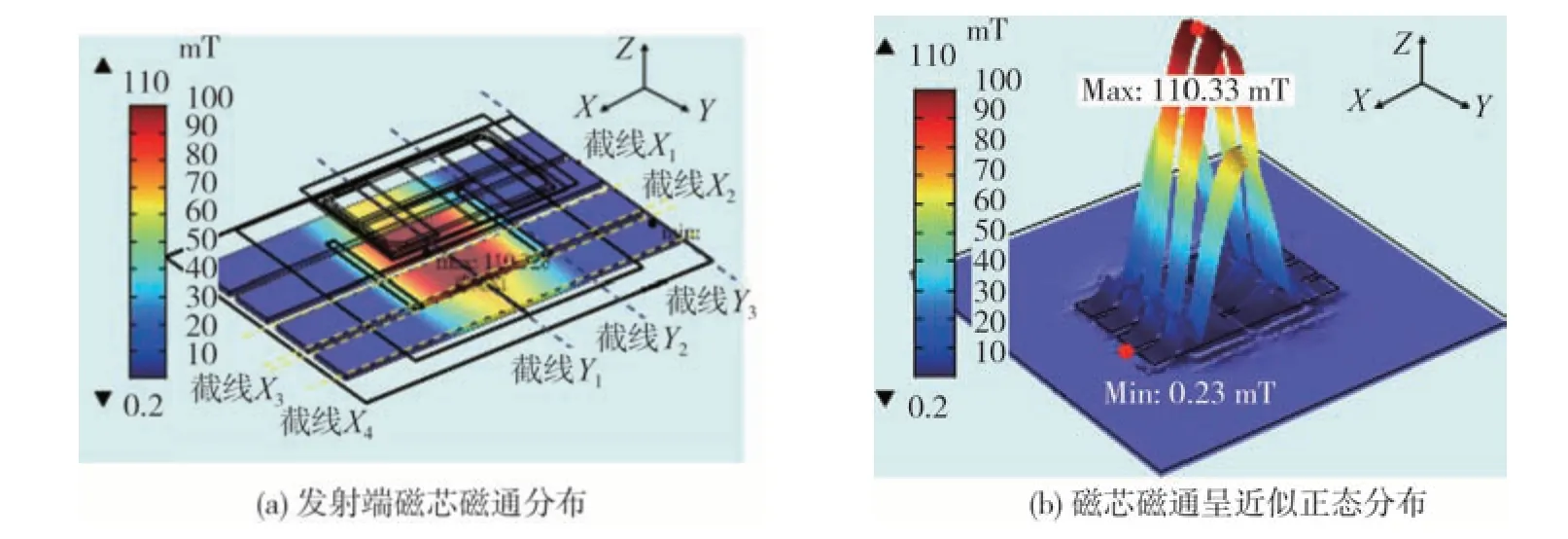
图6 11 kW下参考发射端磁芯磁通密度分布

为定量表征磁芯磁通均匀性，定义磁芯磁通的均匀系数CV（B）作为不同磁芯结构磁通均匀性的评价指标，用不同位置处磁芯的磁通密度分布标准差σ(B(x，y，z))与平均磁通密度的比值表示，见式（6）。均匀系数CV（B）不随线圈安匝数与磁芯均匀厚度变化，可客观反映磁芯磁通的波动性［25］。CV（B）越小，波动性越小，磁芯磁通越均匀，反之CV（B）越大，波动性越大，磁通越不均匀。

2.1 磁通均匀性与磁损耗关系

为研究磁芯磁通均匀性与磁损耗的定量关系，改变发射端磁芯结构及参数，分析磁芯磁通密度、均匀系数以及磁芯损耗的变化。保持发射端磁芯总体积及XOY截面积不变，提出图7 中 3 种非均匀程度较大的磁芯，并改变其XOZ截面形状。考虑到铁氧体脆性难加工，H2至少为2 mm，L1根据图6（a）中磁通分布定为200 mm，在一定范围内参数化扫描3 种磁芯截面的上边X，得到3 种磁芯的均匀系数与磁通密度以及磁芯损耗的关系，如图8（a）和图8（b）所示。磁芯形状变化引起均匀系数在一定范围内变化，其中类梯形2 的均匀系数变化范围最小。特别地，当磁芯体积一定时，3 种磁芯的平均磁通密度不变且与参考发射端磁芯一致，约31.5 mT。而均匀系数与磁芯损耗则为图8（b）中的正相关映射关系，均匀系数越大，磁损耗越大，证明了磁芯磁通的不均匀分布将直接影响磁损耗大小。

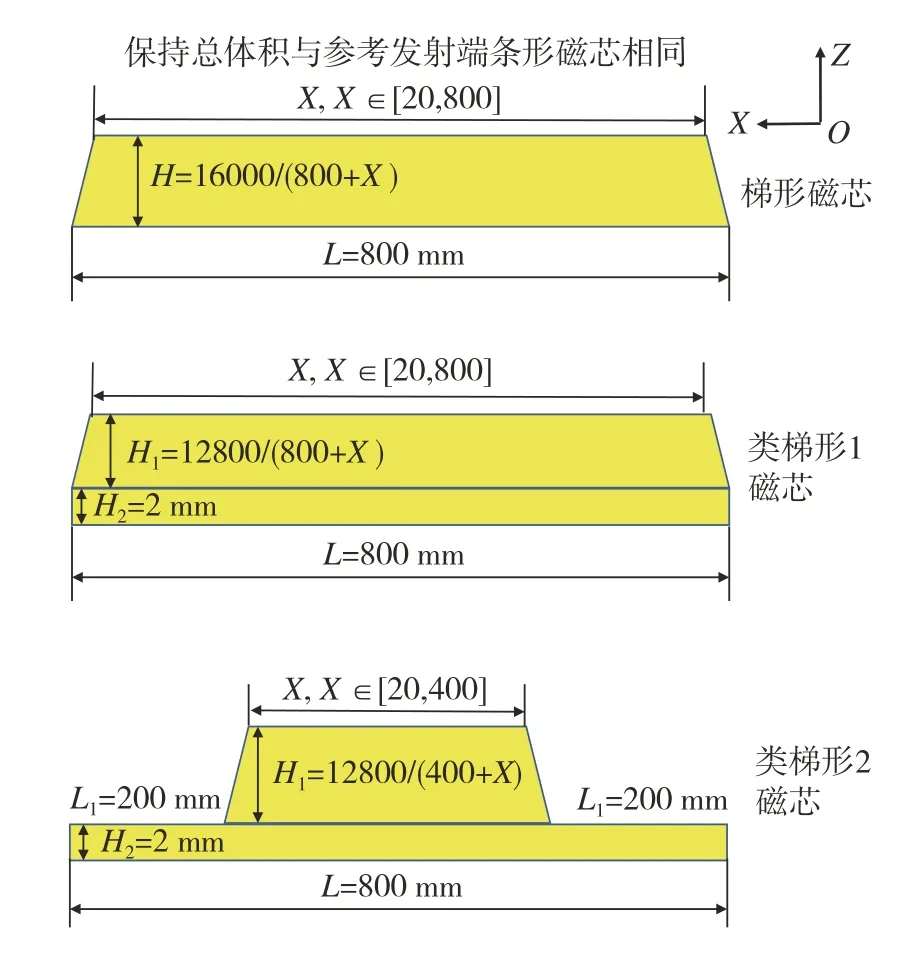
图7 相同体积下3种不同磁芯的截面参数

图8 发射端磁芯损耗与磁通均匀性和磁芯体积的关系

进一步地，磁芯体积一定时，式（6）表明改变磁芯形状理论上可将均匀系数降至0，此时磁通标准差为0，磁芯磁通完全均匀分布，据此由式（2）算得发射端磁芯损耗最小可降至11.98 W。结合图8（b）数据拟合得到一定体积下不同形状磁芯的损耗与均匀系数定量表达式（7），其中磁芯最小损耗值Pcore_min_v=11.98 W，磁损耗系数K=1.56，β=2.4，拟合相关度R2=0.9987。此时，仿真算得参考发射端磁芯的均匀系数为1.113，代入式（7）算得对应磁损耗为36.14 W，接近仿真积分值38.02 W。

为充分体现磁通均匀化优势，考虑在更小磁芯体积下进行优化，以获取最大化收益。定义磁芯体积削减系数α∈（0，1］，表示削减磁芯厚度后磁芯体积占原参考磁芯体积的百分比。建立不同磁芯体积与最小磁损耗的定量关系，拟合可得不同磁芯体积削减系数α与最小磁损耗Pcore_min的关系如图8（c）与式（8）所示。由此可知，随着体积削减系数的减小，最小磁芯损耗先缓慢增加再急剧增加，曲率拐点在削减系数等于0.4 处，说明参考发射端磁芯铺设过量，未被充分利用，磁损耗改善空间较小。

综上，一定磁芯体积下，均匀系数可作为使磁芯损耗最小化的优化方向，但一味减小CV（B）追求磁芯损耗的最小化将导致磁芯结构复杂化。同时，过度削减磁芯体积将显著增加磁芯损耗。因此，在磁芯结构的设计优化过程中，须综合权衡磁芯磁通均匀化与磁芯体积小型化带来的收益与不利因素。

2.2 新型磁芯结构的参数敏感性分析

图7中3种磁芯调控范围有限，且较难实现斜切面加工。为提出一种调控范围更大且易实现的新型磁芯结构，保持发射端磁芯XOY截面不变，根据图6中磁芯磁通分布规律，采用厚度梯度变化易加工的多阶梯层磁芯结构，以减小磁通均匀系数。同时，根据1.2.2节的等效磁路模型，通过在互耦合区2对应的线圈两空心位置铺设磁芯凸台，进一步增强线圈耦合能力。最终，得到如图9 所示的四凸台阶梯层磁芯结构，其中Lall为磁芯总长，4 个磁芯凸台位于内侧两铁氧体条之上，线圈左右极各2 个，凸台宽度等于线圈空心宽度20 mm，高度为T0，凸台深度等于单条铁氧体宽度100 mm，磁芯各阶梯层厚度从大到小分别为T1、T2、T3、T4，对应各阶梯层长度分别为L1、L2、L3、L4。

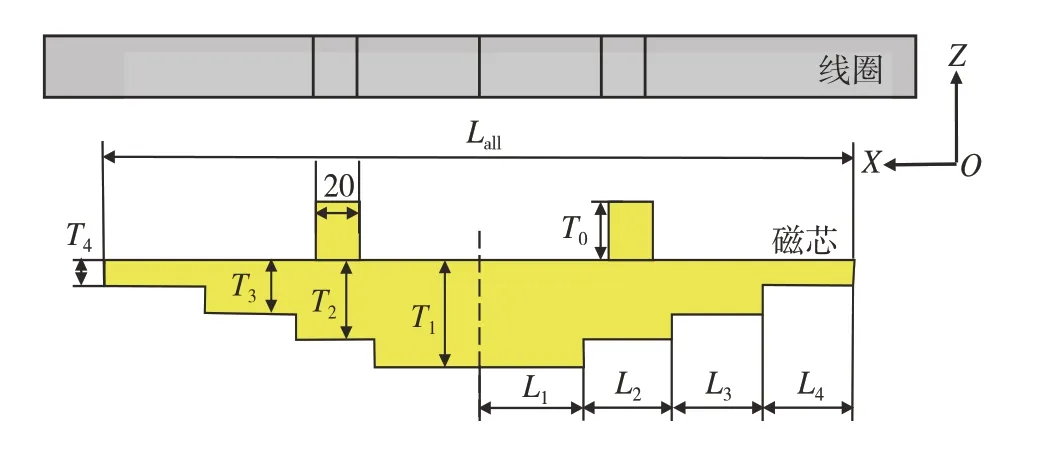
图9 发射端新型磁芯结构的XOZ截面图

为避免磁芯参数的输入维度过高导致优化时间过长并陷入局部最优，对上述10 个输入变量作关于磁通均匀系数与耦合系数的参数敏感性分析，筛选对优化目标敏感且相互制约的参数。设定10 个输入变量的初始值见表1。初始磁芯结构与参考磁芯的体积相同，并按表中给定范围变化，当对单个参数进行分析时，其他参数固定为初始值。而当各阶梯层长度按百分比A1/2/3/4变化时，维持磁芯初始总长不变，仅改变相邻阶梯层长度，具体为A1增大则A2减小，A2增大则A3减小，A3增大则A2减小，A4增大则A3减小。

表1 四凸台阶梯层复合磁芯结构的参数设置

2.2.1 磁芯总长Lall

由于参考磁芯体积削减拐点值为0.4，为避免体积削减过多导致磁损耗过大，Lall最多减小至400 mm。图10（a）为磁芯长度变化下线圈耦合性能与磁通均匀性的敏感性分析结果。随着磁芯长度减小，耦合系数先增大再减小，在440 mm 处取得极大值，原因为参考线圈两侧磁芯过长导致自耦合区3的漏磁阻减小，更多发射线圈漏磁通受两端磁芯的引导重回发射端，未与接收端耦合，证明了所提等效磁路模型的有效性。同时，随着磁芯长度减小，磁芯磁通趋于均匀分布，CV（B）最低降至0.25，说明适当削减磁芯长度可提升磁芯利用率。

图10 发射端新型磁芯的参数敏感性分析结果

2.2.2 凸台高度T0

由于磁耦合结构的厚度及封装要求，4 个磁芯凸台不许超过发射线圈上表面，因此设定凸台高度上限为20 mm。如图10（b）所示，当4 个凸台增加至20 mm 时，线圈耦合系数单调增加，说明增加凸台高度增强了互耦合区2 的导磁能力，线圈间耦合得到增强。而磁通均匀系数CV（B）单调增加，说明凸台磁芯的引入打破了原阶梯层磁芯的磁通均匀化趋势，导致磁通分布趋于不均。因此，T0的变化对线圈间耦合与磁通分布均匀性的改善存在相互冲突。

2.2.3 各阶梯层长度占比A1/2/3/4

当磁芯各阶梯层长度占比从25%变化到50%，结果如图10（c）和图10（d）所示。由于其他结构参数固定不变，磁芯XOY截面的耦合面积不变，因此磁芯各阶梯层长度对线圈耦合系数的影响不敏感，对磁通均匀系数则较敏感，随A1与A2增大，各自相邻且具有更薄厚度的A2与A3减小，因此图10（d）中均匀系数CV（B）增大，即A2与A3趋向于更薄的初始厚度；而A3增大导致A2减小，CV（B）先减小后增大且在A3与A2分别占比40%与10%时最小；而A4增大使A3减小，CV（B）减小，即A3也趋向于更薄的初始厚度。

2.2.4 各阶梯层厚度T1/2/3/4

磁芯各阶梯层厚度变化均从初始设定厚度向下逐渐减小，且厚度的扫描下限值不小于相邻较薄阶梯层的厚度。如图10（e）和图10（f）所示，当各阶梯层厚度逐渐减小时，线圈间耦合系数与互感的变化均不敏感，仅当两侧厚度T4减小至0 时有显著增加。因此磁芯厚度变化不会影响磁芯耦合面积变化，即耦合性能几乎无变化，仅当T4厚度为0 时等效为磁芯总长Lall减小，漏磁阻增加，此时耦合性能增加。

综上，合适的磁芯总长可改善新型磁芯的耦合性能与磁通均匀性，并决定了各阶梯层参数的调优方向，因此固定优化中磁芯总长Lall为440 mm。而磁芯凸台高度T0、各阶梯层长度L1/2/3/4，以及各阶梯层厚度T1/2/3/4的变化对耦合系数与均匀系数的改善则相互冲突，无法通过单参数扫描得到最优解，因此下文将采用多目标优化算法对剩下9 个参数做优化分析。

3 新型磁芯结构多目标优化与验证

为解决磁芯多目标优化过程中目标间冲突，基于Pareto 前沿采用带精英策略的非支配排序多目标遗传优化算法（简称NSGA-II）［26］，通过目标间平衡取舍，使总体目标尽可能达到最优，NSGA-II 算法的基本流程见图11。

图11 NSGA-II算法的基本流程

3.1 优化目标及约束边界定义

3.1.1 优化目标定义

线圈间耦合系数决定了其传输性能好坏，耦合系数越高，则线圈传输效率与功率携带能力越强。因此，选择耦合系数k作为其中一个优化目标。此外，发射端磁芯的磁通不均匀性表现在磁芯两侧的磁通过低的区域利用率低，存在体积浪费。同时，磁通均匀性与磁芯损耗具有正向关系，即磁通越不均匀，磁芯损耗越高。因此，为提升磁芯利用率，改善磁芯体积损耗，将磁通均匀系数CV（B）作为另一优化目标。综合考虑两个优化目标，以期在保持高耦合性能的同时优化得到高利用率的磁芯结构。

3.1.2 优化约束边界

基于本文应用场景，为使整个优化过程能快速收敛至目标最优解，给出优化约束边界如表2 所示，并进行逐一说明。

表2 发射端磁芯多目标优化的约束边界

（1）磁芯最大磁通限值

由于线圈完全对准时，磁芯具有最大的磁通密度值，所以选择线圈完全对准时进行研究。对优化过程中磁芯最大磁通密度值Bmax进行约束，要求不超过损耗拐点值200 mT，以避免磁损耗过高并发生磁饱和。

（2）线圈激励电流

线圈激励电流值会影响磁芯磁通上下限，为准确模拟11 kW 下磁芯磁通分布，支撑后文优化结果的实验验证，根据图3 中系统拓扑方案与线圈最小损耗设计原则［23］，推导得到收发线圈电流见式（9）。算得发射线圈电流I1_RMS为恒定值34 A，接收线圈电流值I2_RMS则受互感变化而变化，优化过程中须随磁芯参数变化实时提取线圈间互感值并代入计算I2_RMS。

（3）新型磁芯的总体积

为避免磁芯体积减小过多导致磁芯最小磁损耗过大而失去优化意义，以参考发射端磁芯的体积削减系数拐点值0.4 为基准，将磁芯的体积削减系数约束在0.4～1之间。

（4）9个输入变量及2个优化目标

考虑到优化迭代时9 个输入变量均在一定范围内随机取值，因此为减少迭代次数与优化时间，基于敏感性分析结果逐一确定9 个输入变量取值边界。首先，设定优化中凸台高度在0～20 mm随机取整；同时，为保证磁通均匀性调控有足够优化空间，各阶梯层长度占比A1/2/3/4均在10%～50%范围内随机取整，且要求A1+A2+A3+A4=100%；而考虑到铁氧体磁芯不易过薄加工，各阶梯层厚度值T1/2/3/4须不小于4 mm。最后，考虑发射端厚度与封装要求，T1/2/3/4不可超过16 mm。对于2个优化目标未作特别要求，仅要求优化后磁芯结构的耦合系数大于参考磁芯的值0.289，而优化后磁通均匀系数要求尽可能小于参考磁芯的值1.113。

3.2 多目标优化流程及结果分析

基于COMSOL 与Matlab 多目标联合优化仿真，经30 h 迭代计算后，得到所有种群关于两优化目标的分布结果如图12（a）所示。随着迭代进行，种群目标值趋于减小，得到Pareto 前沿最优解如图中红色点。提取并重新绘制的两优化目标值相互制约，如图12（b）所示，图中磁通均匀系数减小到0.3及以下后，提升均匀性所带来的磁损耗减小收益可忽略不计。同时，为保证耦合系数尽可能大，最终选取图中耦合系数为0.312（其倒数为3.201 8）且均匀系数为0.301 4对应的新型磁芯结构作为本文的优化结果。

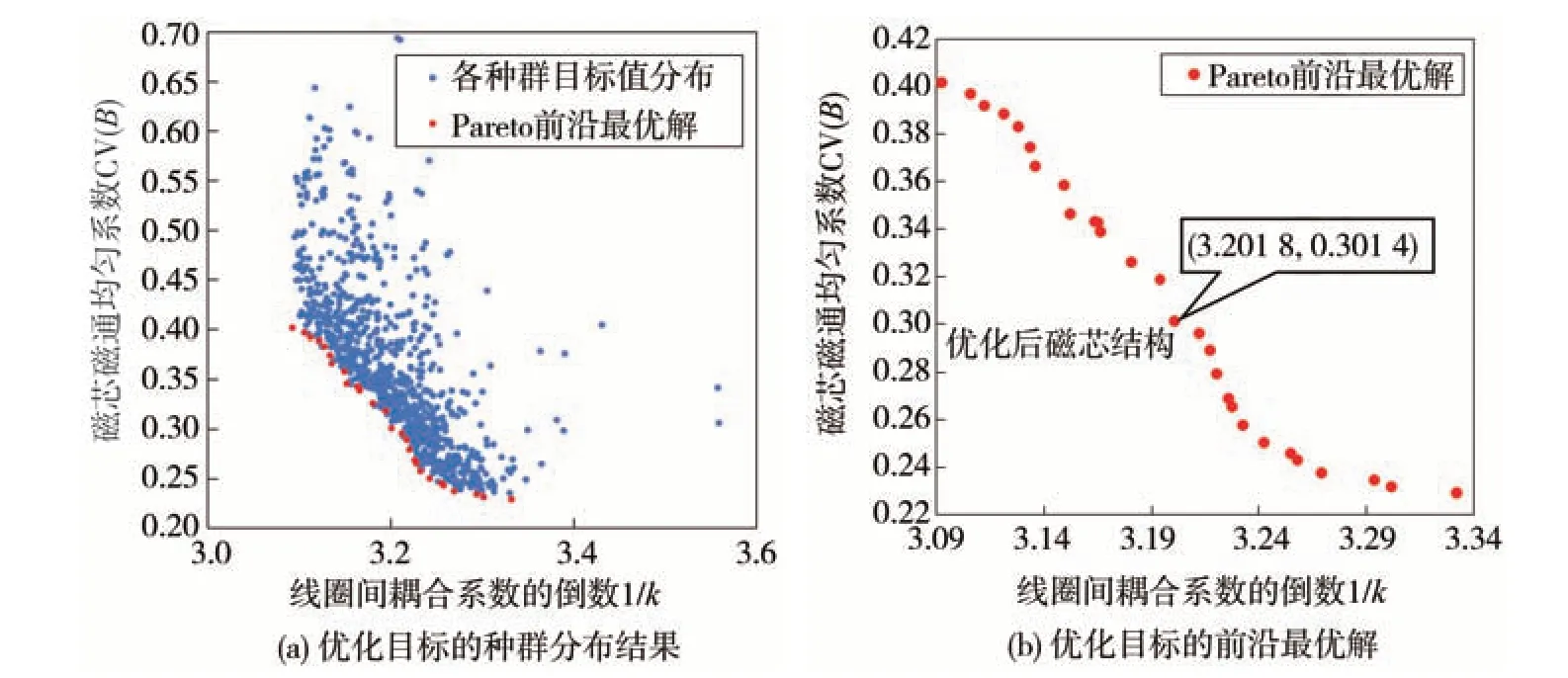
图12 发射端磁芯的多目标优化结果

优化前后发射端磁芯结构对比如图13 所示。优化后磁芯具有4个凸台与4个阶梯层，相比参考磁芯的耦合系数0.289与均匀系数1.113均有改善，仿真积分的优化磁芯损耗值为27.98 W，低于参考磁芯的39.02 W，验证了优化的有效性。同时，经计算，优化后磁芯体积仅为原参考磁芯的60%，满足表2 中体积削减系数的约束范围，磁芯得到了高效利用，减小了体积成本。

图13 发射端参考磁芯与优化磁芯的结构对比（mm）

3.3 优化磁芯的11 kW实验验证

为验证磁芯优化的有效性，搭建如图14 所示的11 kW 实验测试台架，分析磁芯优化前后系统性能变化。20 kW 直流源与12 kW 直流电子负载可保证系统11 kW 功率输出。功率分析仪配合高精度霍尔传感器可实现线圈高频交流侧的有功功率及损耗计算。图14右上角为参考线圈实物图，右下角为优化后磁芯实物图，考虑到磁芯阶梯层在发射端背部呈倒置状态，为防止其结构不稳，图中根据不同阶梯层厚度引入了相应厚度的绝缘橡胶块进行限位支撑处理。

图14 优化磁芯的11 kW实验台架

3.3.1 线圈静态参数分析

在线圈间完全对准且150 mm 垂直气隙下，利用LCR 仪测量优化前后线圈组的耦合参数。为在磁芯替换导致发射线圈自感变化后仍保持系统高效稳定运行，重新匹配发射端补偿参数。同时，为分析11 kW 下优化前后发射线圈各组件损耗分布，须分离各组件等效电阻。根据2.1 节中的等效电路模型与文献［25］，利用LCR 仪分别测量85 kHz 下单线圈、线圈+磁芯、线圈+磁芯+铝板的等效电阻，剥离得到优化前后发射端线圈与铝板等效电阻值，汇总如表3所示。

表3 优化前后线圈耦合参数及阻值测量结果

相比参考线圈，优化后发射线圈电感值与耦合系数均增大，线圈携带功率能力与理论传输效率提升。从等效电阻值看，由于仅改变优化前后的磁芯结构，因此线圈等效电阻基本不变。得益于磁通均匀化调控的贡献，优化发射线圈的总电阻低于参考磁芯，理论损耗更小。而由于优化磁芯总长度的减小，发射线圈两端磁通失去了磁芯的引导屏蔽，导致更多磁通泄漏至铝背板上，优化后铝板等效电阻增大。

3.3.2 线圈传输性能及损耗对比分析

进一步地，测量优化前后的线圈间传输效率，结果如图15（a）和图15（b）所示。当线圈完全对准时，优化后线圈传输效率略高于优化前，二者均在98%以上，优化后线圈间损耗低于优化前，为220 W。同时如图15（c）和图15（d）所示。优化后磁芯的系统功率可稳定输出11 kW，其传输效率91.918%高于优化前的磁芯。

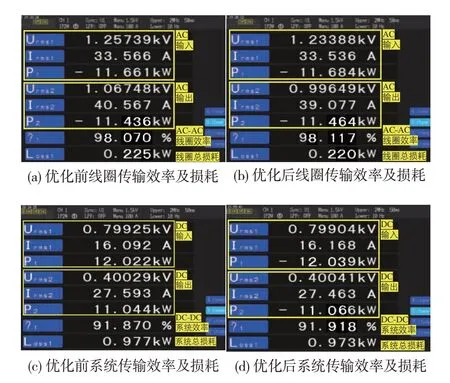
图15 发射线圈优化前后的传输性能对比

最后，根据图15 中实测发射线圈的交流电流值与表3 中线圈与铝板等效电阻值，计算得到发射端各组件损耗分布，如图16 所示。通过均匀化调控，剥离得到的磁芯损耗减少约10 W，且其实验计算值与理论和仿真值均接近。

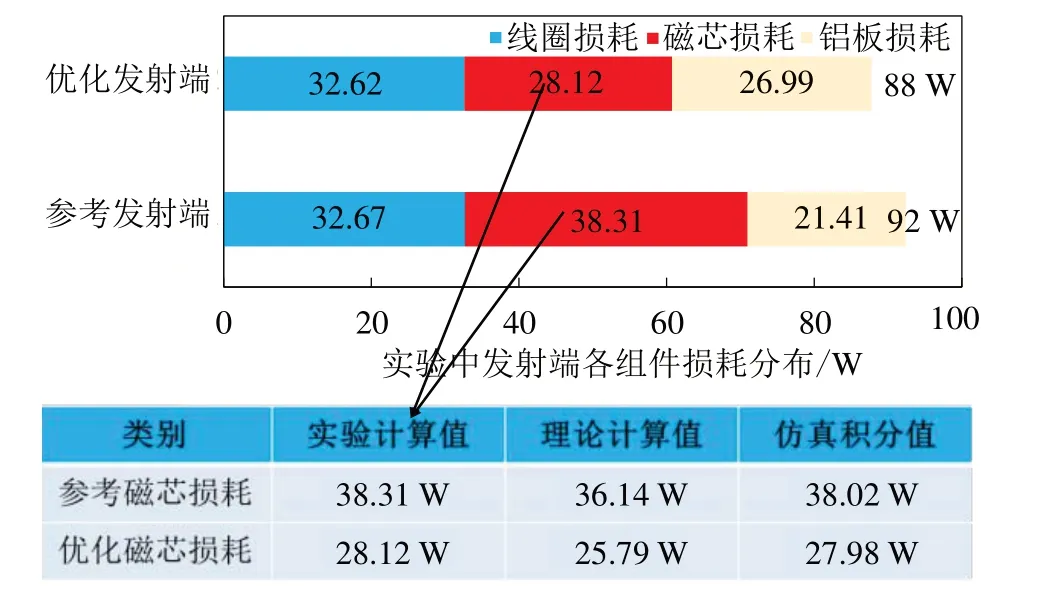
图16 发射线圈各组件损耗对比分析

综上，本实验验证了磁芯多目标优化的有效性，虽然优化后磁芯结构受铝板漏磁的影响，11 kW 下传输效率及发射端总损耗改善较小，但证明了通过磁通均匀化调控减小磁芯损耗的有效性。同时，优化后的磁芯体积仅为原参考磁芯的60%，说明通过磁通均匀化调控，磁芯体积得到了更加高效的利用。

4 结论

根据本文研究工作，总结研究亮点如下。

（1）基于选定的非对称DD 线圈组，建立了其等效电路模型与等效磁路模型，为分析磁耦合各组件损耗与磁芯的排布设计提供了理论指导依据。

（2）提出了磁芯磁通均匀性评价指标，建立了磁通均匀系数与磁芯损耗及磁芯体积间的定量关系，为磁芯结构参数的设计提供了理论指导依据。

（3）基于COMSOL与Matlab联合优化，提出了高效高利用率新型磁芯的多目标优化设计方法，并从磁芯损耗、传输效率、磁芯体积等方面实验验证了所提方法的有效性。

随着大功率无线充电技术的发展，对磁芯工作条件与体积成本的要求愈加严苛，本文中高效高利用率磁芯考虑了不同位置处磁芯的合理调控，符合磁芯大功率、小体积的发展趋势。