带除法器的铝合金型材挤压系统温度闭环控制研究

黄艺娜

(漳州职业技术学院 智能制造学院,福建 漳州 363000)

0 引言

在铝合金型材挤压过程中铝锭温度高,金属的变形抗力小,为加快挤压的速度,提高挤压机的生产效率,普遍采用热挤压,铝锭坯被加热到440～480℃后送入挤压容室。但金属塑型变形及摩擦发热会导致铝锭的温度进一步升高,使出口型材的温度和力学性能沿长度方向发生变化,甚至产生扭曲、裂纹等质量缺陷,因此挤压过程带来的温度升高又制约着挤压速度提高。为获得较高的生产效率并保证产品质量,最好采用等温挤压技术[1-4],即在挤压过程中保持挤压变形区的温度恒定。目前等温挤压有三种实现方法:铝锭的梯温加热[5]、挤压参数的热—力耦合仿真[6]、参数双闭环(挤压速度—型材出口温度)挤压控制[7-8]。这三种方法各有优势,可以根据不同应用场合互相组合,发挥最佳效果。

针对等温挤压的研究虽然不少,但大多数研究关注于温度开环即模拟等温挤压技术。文献[9-10]构建型材出口温度—挤压速度闭环,根据出口温度实时调整挤压速度,以实现等温挤压。

出口型材温度变化,归根结底是由挤压力做功而导致的,要控制出口型材温度,应当以挤压功率做为控制力。挤压功率的两个要素为挤压力和挤压速度,挤压力与挤压速度、铝锭变形区温度、合金牌号、锭长、挤压比等工艺参数有非常复杂的关系,在挤压过程中会发生实时变化,如果忽略挤压力的变化,只调节挤压速度将使得实际控制力偏离期望值,难以得到期望的控制效果[11-12]。

本文着重研究以挤压功率为控制力的控制系统结构[13-14],在此基础上提出一种简化的挤压功率-型材出口温度模型控制系统。

1 铝挤压机制品出口温度模型

铝型材挤压生产线是一个复杂的生产过程控制系统,整个工艺可按“加热—挤压—淬火—锯切—矫直”的流程进行生产,可概括为三个阶段:

(1)铝锭加热阶段:将由前端的冷锯系统送出的一定规格的铝锭送入工频感应炉预热,使铝锭获得工艺要求的初始温度,也可使铝锭在其轴向上具有梯度温差,实现梯温加热。

(2)铝锭的热挤压阶段:将受热软化的铝锭通过上锭装置送到挤压机,装进已经预热好的挤压筒,并装载模具。由液压系统的主侧缸提供动力推动挤压杆向前挤压铝锭,使铝锭在模具口处因受挤压而产生变形,从不同规格的模具流出,获得相应形状的型材制品。

(3)铝型材的后处理阶段:挤压完成后的型材,组织性能还不稳定,需要进行在线淬火和冷却,使型材不会扭曲变形;再经过牵引机和飞锯将铝型材进行锯切,送入冷床进行时效处理,提高型材品质。

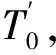
ΔT0=G1·W

(2)

其中G1表示在挤压力总做功中导致变形区温度变化的那部分能量,可用图1(a)表示式(1)-(3)。

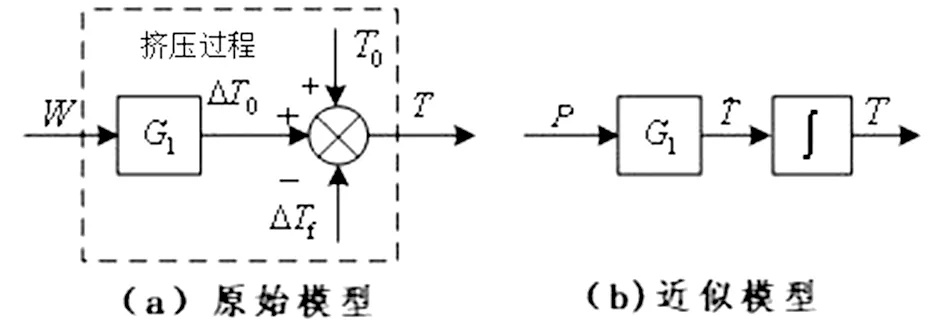
图1 出口温度模型结构图

考虑到在短时间内ΔTf近似相等,可以得到:

ΔT≈ΔT0=G1·W

(4)

其中ΔT为两次测量得到的型材温度变化值,利用式(4)进一步得到:

其中P为实时挤压功率。式(5)是一个单输入单输出的简化模型,结构如图1(b)所示。

2 闭环温度控制系统结构

式(5)表明,控制型材出口温度变化的控制力应为挤压功率P=F′·v,其中F′=Ff+Fd为摩擦力Ff与金属变形抗力Fd之和,v为挤压速度。在不考虑牵引力情况下,挤压力F与挤压速度v之间需满足牛顿第二定律:

其中m为挤压轴、铝锭及型材制品等总质量,为了将F′与F进行区分,称F′为有效挤压力(即直接参与做功,使得型材温度发生变化)。

文献[4-6]以挤压速度为控制力,可以认为是将Ff和Fd视为常数,这与实际情况相违背,实际挤压功率在挤压进程中会发生变化,只通过调节挤压速度难以得到期望的挤压功率,这将直接影响对型材出口温度的控制效果。为了消除挤压力变化的影响,考虑到挤压力可实际测得,可在温度调节器的输出增加除法器,具体如图2所示。

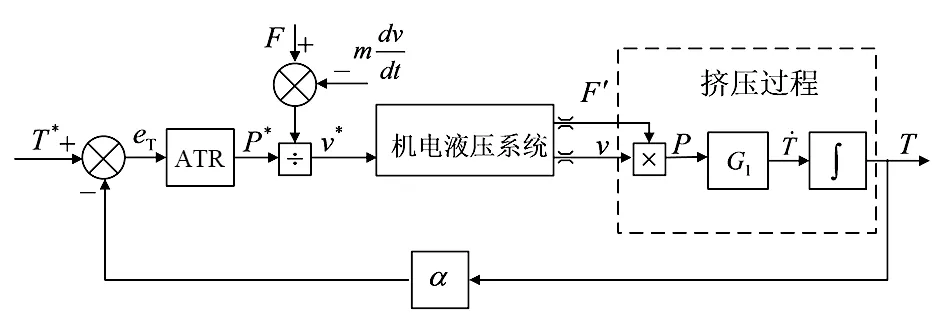
图2 闭环温度控制系统结构图

图中温度偏差eT送入温度调节器ATR,调节器输出给定功率P*,给定功率除以F′后得到给定挤压速度v*,F′可根据式(6)计算得到,图中除法器能够及时调整v*,抵消F′变化对功率输出的影响。

3 仿真平台建立

为了说明前一节中除法器的作用,文中对图2的系统进行仿真。为了简化仿真模型,可忽略挤压速度的过渡过程。除了需建立挤压过程温度模型外,为了说明有效挤压力的变化,还需要建立有效挤压力与温度的模型。

型材挤压过程热力学模型为一组非线性、时变、强耦合的偏微分方程组,直接建模困难,也难以根据该模型设计控制器。对于难以直接建模的系统,可根据输入输出数据应用系统辨识方法确定对象模型[11-13]。文献[7]应用神经网络技术建模,但计算量大,模型训练时间长,本文采用一次完成最小二乘法同时确定的模型结构和参数。

3.1 模型结构建模

用自回归滑动平均模型来描述输入输出关系:

A(z-1)y(k)=z-dB(z-1)x(k)+ξ(k)

(7)

式中y(k),x(k)——k时刻型材温度和输入功率;ξ(k)——k时刻随机噪声;d——控制通道时延;z-1——单位后移算子;

k=1,2,3,…

移项整理后写成下列简洁形式:

y(k)=φT(k-1)θ+ξ(k)

(8)

式中φ(k-1),θ——数据向量和参数向量;

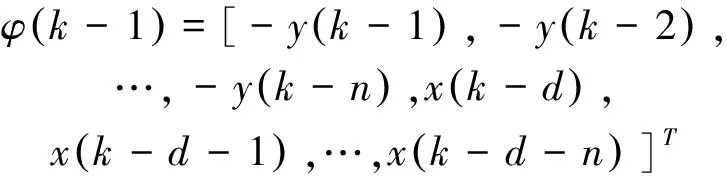
θ=[a1,a2,…,an,b0,b1,…,bn]T

确定模型结构和参数流程如图3所示。

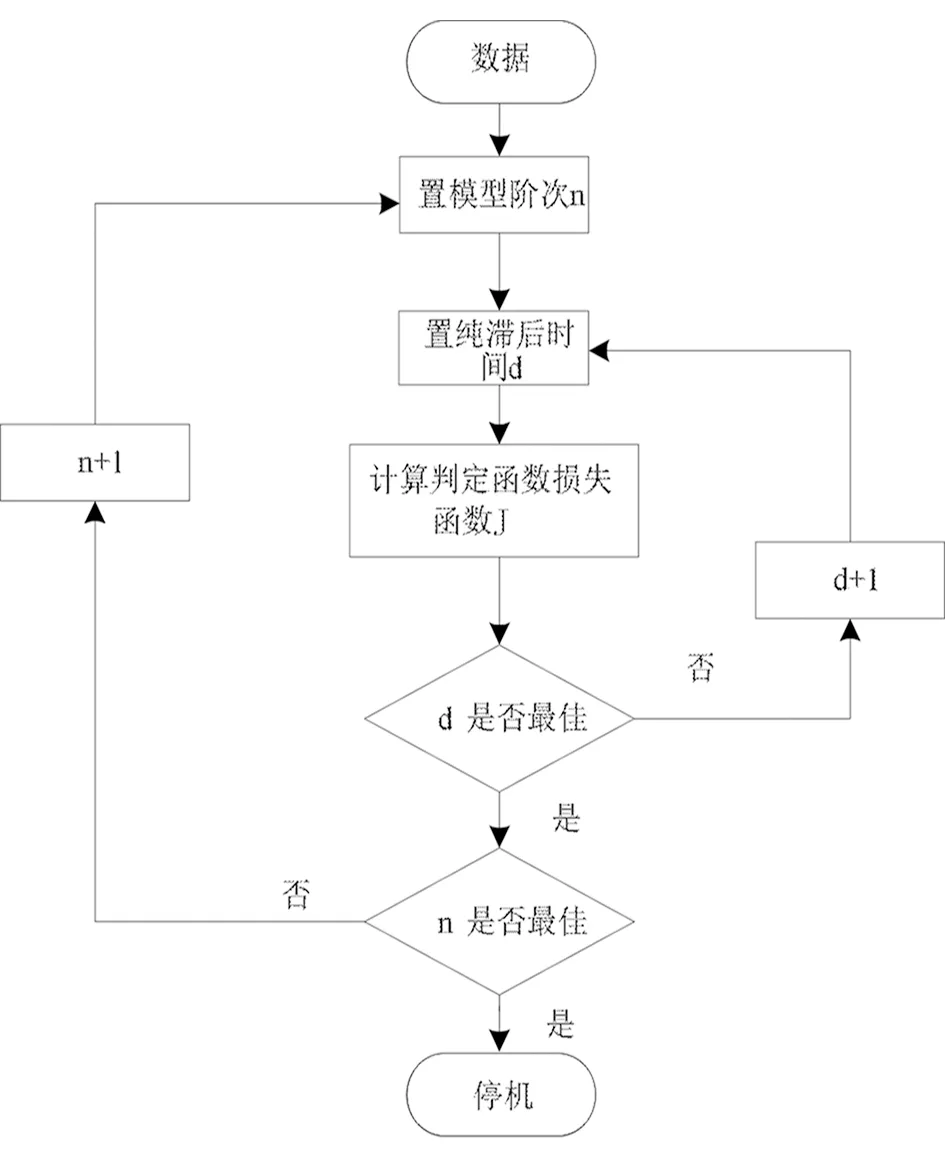
图3 模型辨识流程图

图3中d为纯滞后时间,n为模型的阶数,J为损失函数,按式(9)计算:

3.2 模型辨识结果及验证

按上一小节算法得到型材出口温度和有效挤压力模型分别为[11-13]:

测得某大型挤压机生产6061合金、Y5439(断面号)工业型材的一组数据,挤压速度(v)、主缸压力(Pm)和侧缸压力(Pa)、出口型材温度如图4所示。

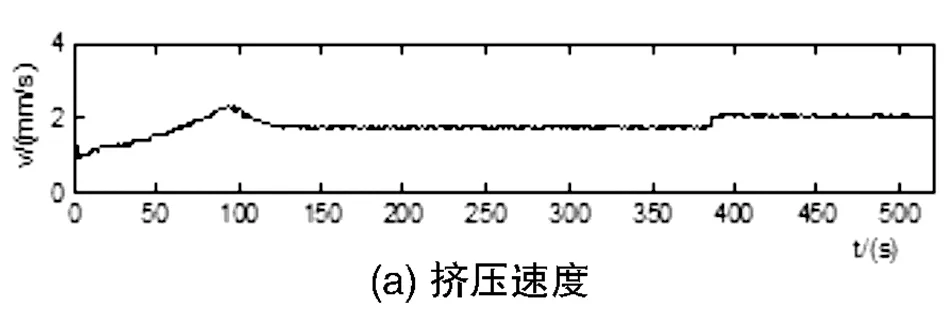
图4 实际数据

用测得的另一组数据对该模型进行验证,结果如图5和图6。从图5和图6可知,实测温度与由模型观测温度之间误差在±10℃内,由式(6)计算得到的实际有效挤压力与观测值误差也很小,因此,可以用式(10)与式(11)模拟挤压过程。

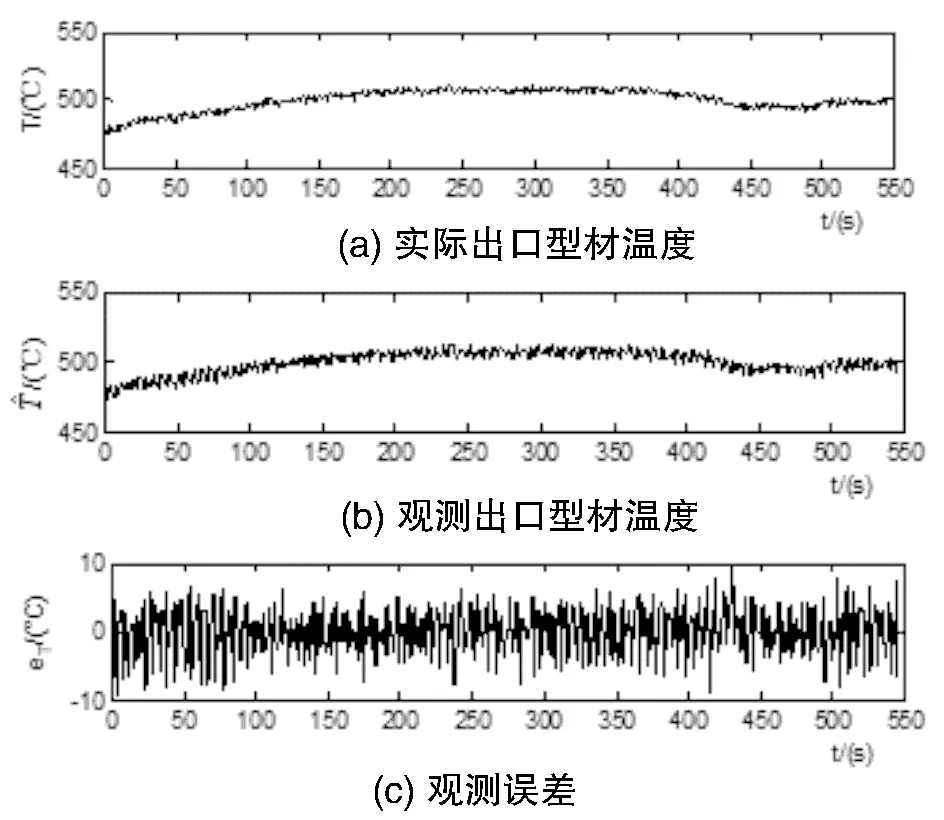
图5 温度模型验证图

图6 F′模型验证图

4 结论

本文着重研究以挤压功率为控制力时的铝型材出口温度闭环控制系统结构。首先,推导简化的挤压功率-型材出口温度模型,其次,提出一种新型的系统结构,消除挤压力波动对实际挤压功率的影响,最后,建立仿真系统平台,并对所提出的系统结构进行验证,为了模拟挤压过程,应用最小二乘法分别确定对象模型的结构和参数。