卫星通信载荷向量化建模方法

黄文乾,刘彧千,李 晓,杨亚宁,赵 光,李殷乔

(1.中国空间技术研究院,北京 100094;2.国家航天局卫星通信系统创新中心,北京 100094;3.中国空间技术研究院 西安分院,陕西 西安 710100)

0 引言

典型的卫星通信载荷是一种放大、变频、滤波、交换、通道交链、通信/导航/数传信号共存、时间/任务管理等多种复杂功能深度耦合且重要单机设置环备份的综合性通信电子处理系统[1]。因设计与研制往往深刻影响卫星寿命期任务成败,所以需要在整个卫星研制周期仔细进行通信载荷链路设计并编排各个试验阶段所需要的测试用例。

然而,随着运载、卫星平台和信息处理等技术不断进步和通信、导航、遥感、组网等需求不断增长,通信卫星载荷正逐渐向大规模、多功能、复杂处理交换等方向发展,传统人工设计和测试用例排布效率极低,无法有效适应正蓬勃发展的卫星研制数字化批产化发展趋势。举例而言,在设计和测试过程中常常需要对链路冗余设计进行遍历测试。传统方法通常采用穷举的方式进行链路遍历:假设每个开关平均有3个状态且通信载荷有200个开关,则整个通信载荷共有3200种可能组合。传统上程序式解决链路问题采用循环遍历方法,然而循环遍历方法的解算复杂度随着载荷规模维度呈指数增长,运算时间和代价极大。

现有载荷建模领域工作主要面向功能性建模和环备份开关设计建模。文献[2-3]对卫星通信有效载荷分系统进行了面向对象的功能性建模。文献[4]提出了一种基于遗传算法的星载功率放大器的备份环开关切换方案,采用选择-交叉-变异的循环模拟生物种群繁殖、竞争、淘汰、平衡的进化过程,来选择较优的开关切换方案。文献[5]通过对图论中关于图形的基本要素以及连通度的研究,对开关备份环进行了图形和数学模型抽象,提出一种新型的开关备份环的设计方法。文献[6]提出了一种基于图论和遗传算法的备份环切换分析方法,该方法首先应用图论中的邻接链表表示法对备份环进行建模,并利用遗传算法进行寻优。文献[7-8]提出了通信卫星转发器备份环开关的若干搜索算法。文献[7-11]提出了转发器功放备份环切换方法的详细过程。

现有载荷建模研究工作尚未面向载荷链路遍历问题,为解决此问题,本文提出一种向量化建模方法,该方法对多条链路同时进行向量化运算,并根据链路逻辑连接状态进行向量压缩防止向量维度爆炸,向量化模型可以以较低的时间复杂度快速得到整个星上通信载荷链路所有可能组合,可在卫星数字化研制各阶段中有着重要应用。

1 向量化建模

复杂的星上通信载荷涉及多类有源单机环备份关系,链路组成和耦合关系较为复杂。本文从易到难,从单链路单状态、单链路多状态、多链路多状态、通用状态建模流程等步骤阐明所提向量化建模方法。

1.1 单链路单状态

图1为通信载荷最简单的单链路单状态,即输入输出链路上有且仅有一条通路,同时链路上设备仅有一种联通状态。

图1所示链路中,链路经过设备依次为A—B—C,其中,将设备A(典型如输入滤波器)建模为一个二端口设备,其输入端口为J1,输出端口为J2,设备A内部连接关系向量化建模为2×2矩阵,如式(1)所示,该矩阵行列物理意义均表示设备A端口[J1,J2],该向量化模型即可表示设备A内部J1与J2相连。

(1)

进一步地,设备A后端与设备B连接,将设备B建模为四端口设备(典型如开关),4个端口分别定义为J1、J2、J3、J4。设备A和B间连接关系向量化建模为2×4矩阵,如式(2)所示,该矩阵行物理意义为设备A端口[J1,J2],列物理意义为设备B端口[J1,J2,J3,J4]。该矩阵可以表示,仅有设备A端口J2和设备B端口J1相连。

(2)

同时,设备B内部链接关系向量化建模为4×4矩阵,行列物理意义均为设备B端口[J1,J2,J3,J4]。如式(3)所示,设备B内部J1和J2相连,J3和J4相连(为便于阐述,假定设备B,典型如开关,仅有当前一种可能状态)。

(3)

根据设备内部和设备间连接关系,将整条链路建模后设备内部矩阵和设备连接矩阵相乘可得链路级向量化模型,如式(4)所示。链路级向量化模型运算结果为2×2矩阵,行物理意义为链路起始端设备A端口[J1,J2],列物理意义为链路终点端设备C端口[J1,J2]。该链路级向量化模型有以下几种物理含义:

① 计算结果表示,链路端对端物理意义上,设备A端口J1和设备C端口J2相连。

② 链路经过的设备为A、B、C。

(4)

1.2 单链路多状态

通常链路存在多个可能状态,主要是链路上可切换设备造成的。基于上节单链路单状态建模,扩展对单链路多状态进行建模。图2中,整条链路经过设备依次为A—B—C—E—F,其中设备B和E为同种设备(典型如C型开关),且内部连接有两种状态:状态1为J1和J2相连,J3和J4相连;状态2为J1和J4相连,J2和J3相连。两个状态可进行任意设置和切换。因此上述链路交叉组合共用4种状态:① 设备B状态1和设备E状态1;② 设备B状态1和设备E状态2;③ 设备B状态2和设备E状态1;④ 设备B状态2和设备E状态2。基于本文建模思路,4种链路状态向量化表示如式(5)～(8)。

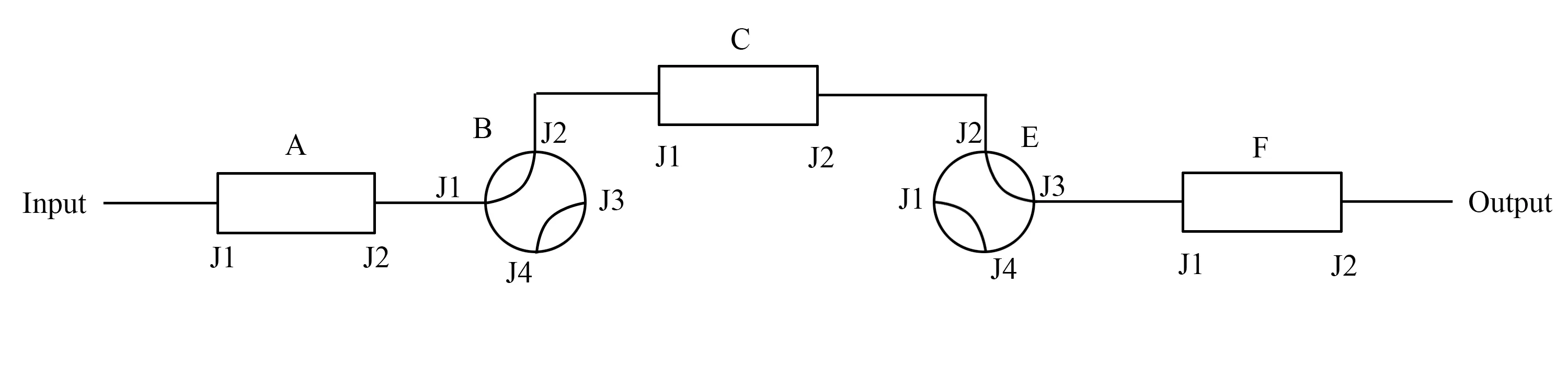
图2 单链路多状态Fig.2 Single-link multi-state

(5)

(6)

(7)

(8)

链路A—B—C—E—F上述4种状态中只有第二种状态:设备B状态1和设备E状态2可使端到端链路畅通,即仅有链路向量化运算结果式(6)中包含1,表示设备A 端口J1和设备F端口 J2有效畅通,其余运算结果中均不包含1,表示设备A和F无法连通。

1.3 基于前向传播思想的多链路多状态向量化建模

以图3链路为例,给出多链路向量化建模过程。图中有两条端对端链路:A—B—C—E—F和A—B—D—E—F。设备B和E均存在两种可切换状态,不同的设备状态组合下,两条链路的通断情况不同,对于上述多链路多状态的向量化建模,需要应用前向传播原理,对多条链路同时进行向量化建模运算,从输入端口传播到输出端口,得到链路级建模结果。建模核心思想是,基于前向传播原理,应用了向量随路对角化扩充来表征多链路,同时为了防止向量维度爆炸,又在随路扩充同时进行随路压缩无效链路、压缩不匹配通道。

1.3.1 随路扩充

图3中,设备A与设备B相连,设备B有两种状态,因此将设备A到B之间的向量化表示以及设备B的两种状态均扩充为对角矩阵;进一步前向传播建模:设备B后端有C和D两个设备,链路会有两种走向,将当前链路向量化模型继续扩充为对角矩阵。

因此,从设备A到设备C和D,链路上共有设备B的两种状态,以及设备C和D的两种链路走向,即共有4种可能性,4种可能性如式(9)所示:

(9)

1.3.2 无效链路随路压缩

将设备内部连接关系和设备间连接关系结果代入上述向量化模型,可得到运算结果,可以看出,只有两种有效链路连通状态:实际对应设备B为状态1(J1—J2相连,J3—J4相连)导通到设备C的链路为状态2(J1—J4相连,J2—J3相连)导通到设备D的链路,如式(10)所示。为防止链路复杂后矩阵维度爆炸,在随路对角矩阵扩充后根据运算结果进行随路压缩,将无实际意义的中间两种状态从矩阵中去掉,压缩后多链路多状态向量化模型如式(11)所示:

(10)

(11)

进一步地,设备C和D与设备E相连,设备E有两种状态,因此链路向量化对角化扩充,再将设备F与链路相连,并将设备内部连接关系和设备间连接关系代入向量化模型并根据运算结果,压缩掉无效链路后,可得最终链路级端对端向量化模型,如式(12)所示:

(12)

多链路多状态向量化模型有两种物理意义:

① 计算结果表示,链路端对端物理意义上,设备A端口J1和设备F端口J2相连。

② 该多链路多状态样例中,共两种可能链路:链路A—B—C—E—F,此链路状态中设备B和E分别为状态1和状态2;链路A—B—D—E—F,此链路状态中设备B和E分别为状态2和状态1。

1.3.3 通道匹配压缩

此外,转发器中需要进行通道匹配。简单的转发器可以利用射频频率/带宽匹配进行,但是涉及极化复用、多色复用的复杂转发器常出现频率/带宽完全匹配的两个通道中不容许连接的设计,因此通道匹配必须提前预设好每条链路必经的通道/节点。

本文所提建模方法采取射频匹配随路压缩,必经节点最终压缩的方式进行通道匹配。假设设计时已预设好仅设备A和设备C的通道能够进行连接,则在上述例子进行设备B和设备C、D连接时,预设通道匹配可以进行进一步向量模型压缩。假设只有设备A和C能射频匹配,设备A和D不存在连接可能,式(13)的向量化模型可以进一步压缩为式(14):

(13)

(14)

1.4 通用转发器向量化建模

基于前向传播随路扩充与压缩思想的链路向量化建模方法,以图4所示更复杂通用转发器系统(多输入、多输出、多链路、多状态)为例,建立通用转发器向量化建模算法。

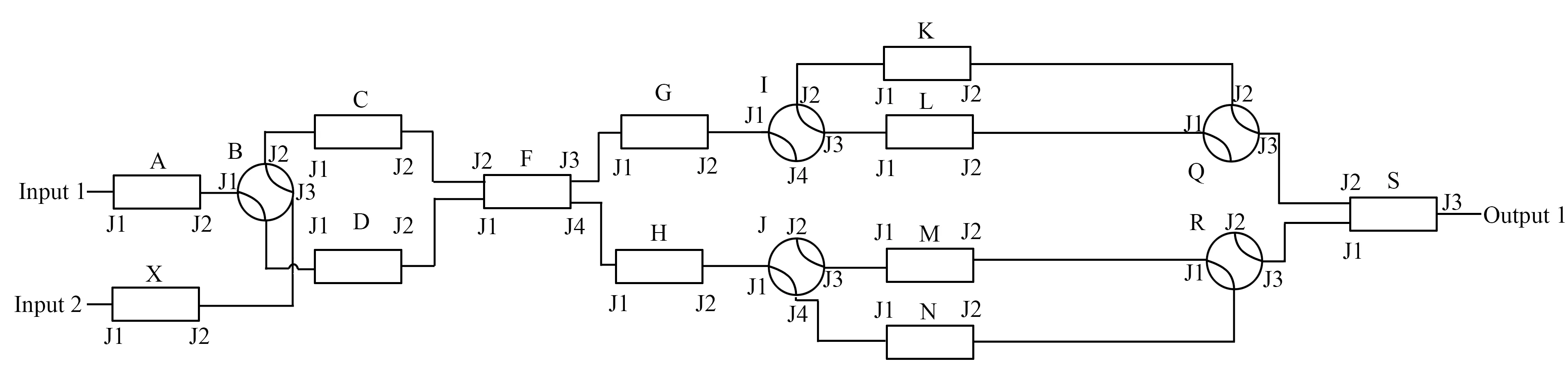
图4 通用状态Fig.4 Generalize state

1.4.1 算法输入

本文提出的通用转发器向量化建模算法需要以下输入:

① 链路数量以及每条链路起始点定义,如表1所示,其中必经点为必经之路;

表1 链路定义Tab.1 Link definition

② 链路中每个设备的特性以及内部、设备之间连接关系,如表2所示;

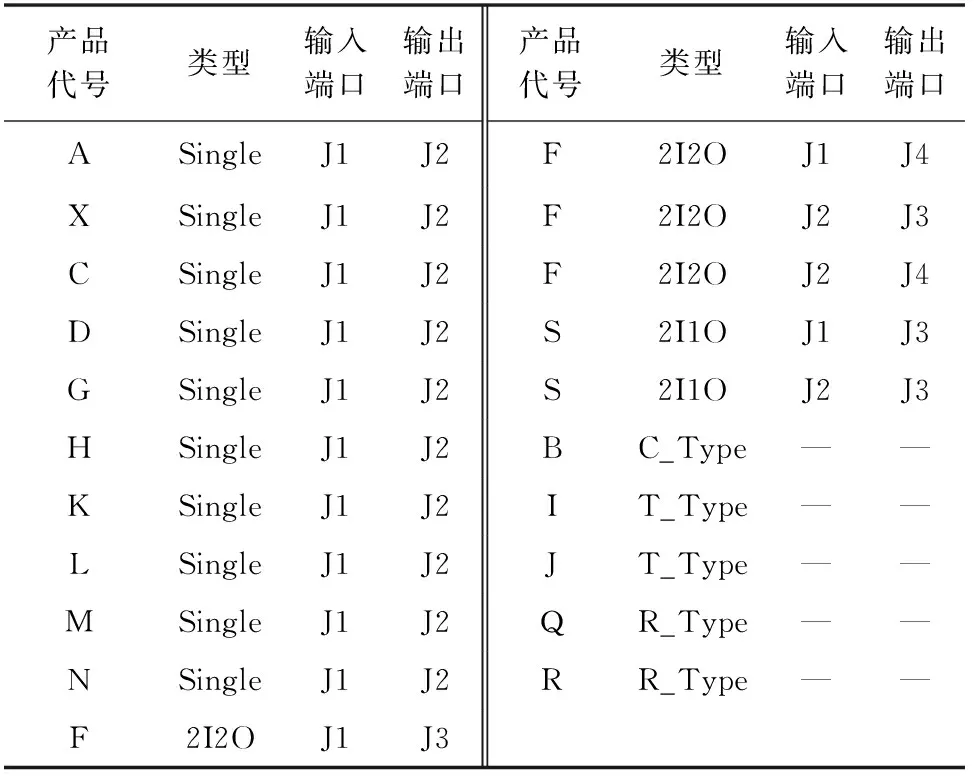
表2 设备定义Tab.2 Device definition

③ 链路中设备间的连接关系和开关状态类型,如表3和表4所示。

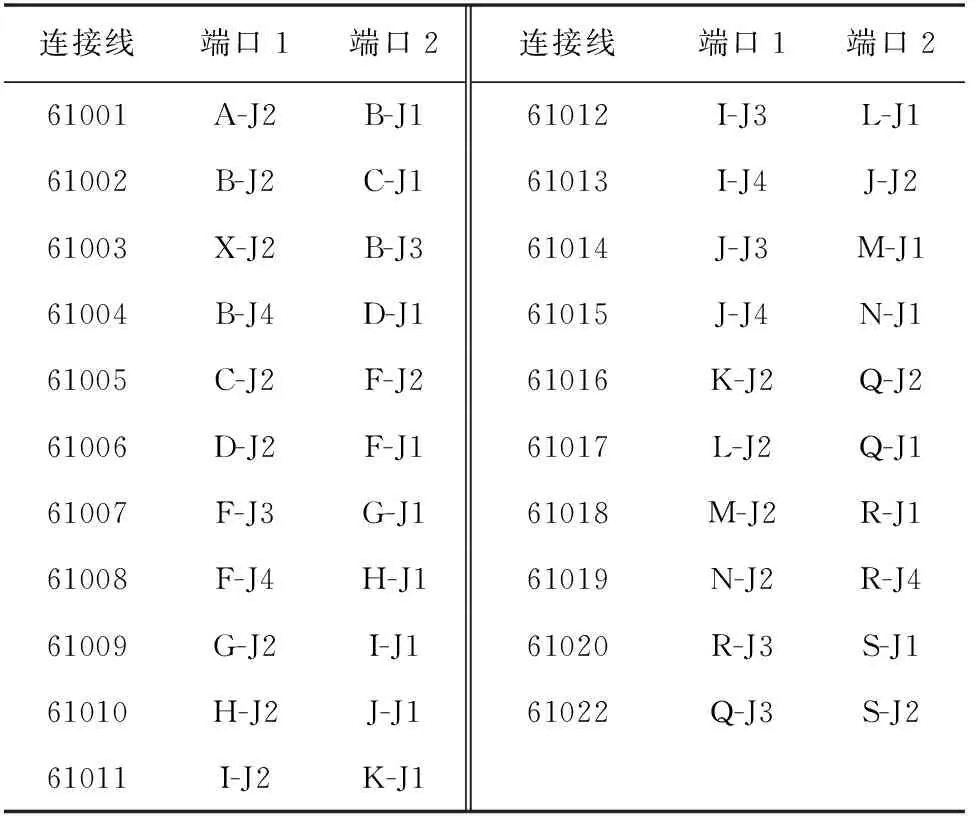
表3 连接定义Tab.3 Connection definition

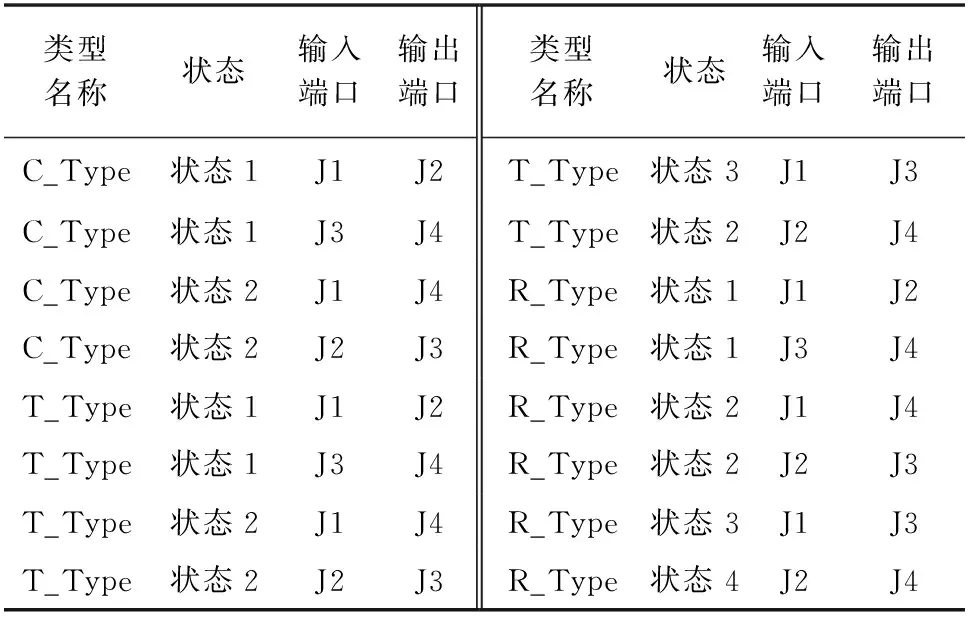
表4 开关类型定义Tab.4 Switch definition

1.4.2 数据结构设计和建模算法

为实现上述建模符号化和向量计算结果双重表示,采用Python中DataFrame数据结构进行向量化模型数据结构基础。利用DataFrame的元素行索引特性,将元素设置为向量化数值,将行索引设置为向量化符号表示。

基于上节应用前向传播随路扩充与压缩思想的链路向量化建模方法,通用转发器向量化建模算法如算法1所示。

算法1 向量化建模算法1) For第i条链路:(遍历链路定义表中的每一行)2) 读取该条链路起点、终点和必经点3) For第q个节点:(前向传播,从起点开始)4) 在设备定义表和连接定义表中搜寻起始点的下个节点5) 如果第q个节点为多状态则进行随路扩充,具体有以下两种情况:6) 情况1多状态同时存在,如F7) 情况2多状态互斥存在,如开关类型定义表8) 进行无效链路随路压缩(只在随路扩充后进行)9) 进行通道射频随路压缩(依据设备定义表中设备特征,每个节点进行)10) 判断链路是否包含终点:如是则跳出循环11) 依据链路定义表中的必经点集合,进行通道匹配压缩12) 得到第i条链路所有可能的路径组合13) 得到所有链路所有可能的路径组合

1.4.3 算法输出

应用表5向量化建模算法,得到每条链路所有可能的路径组合。共两条链路Input1—Output1和Input2—Output1,两条链路向量化运算结果如表5和表6所示,即两条链路各有8种可能的链路路径。

2 复杂度计算与数字化应用

2.1 复杂度计算

传统基于穷举方法的时间复杂度可以推导计算如下。穷举算法是由m层For循环组成(m为转发器开关数量),考虑开关平均有n种状态,最内层For循环的时间复杂度为O(n),结合外层m个For循环,传统穷举算法的时间复杂度为O(nm),该复杂度为指数级别,随着开关数量m的增加,整个算法复杂度会指数级增长,效率极低。

本文所提如表5所示方法的时间复杂度仅有两层For循环:

① 外层For循环复杂度为O(l),l为链路数量。

② 内层For循环内层主要为向量乘法运算。向量乘法的复杂度在1969年由Volker Strassen提出的Strassen算法下降到了O(q)以下[12-16],其中,q为矩阵的最大维度,在本算法中,q应该为所有链路单机数量总和N除以链路数量l再除以单条链路上平均单机数量p,即q=N/l/p。当前高级语言如Matlab、Python等均使用了Strassen算法或者改进型的Strassen算法[17-18]。

因此,本文所提方法时间复杂度为O(l*q)=O(N/p),该复杂度为多项式级别,即复杂度随着单机数量总数N线性增长。所提多项式级别复杂度方法相比传统指数级别方法,极大提升了卫星通信载荷建模效率。

2.2 数字化应用

在卫星数字化设计阶段,需要进行通信载荷第一备份、第二备份的设置同时要求工作链路不能重复,传统方法均为人工走查确认;基于本文所提向量化建模结果,可以在每条链路理论上所有可能路径中进行多链路冲突检测,经过多链路冲突检测后便可得到所有链路同时工作的所有组合,基于已有所有组合进行转发器第一备份、第二备份的设计可以极大减少设计和人工走查工作量。

在卫星数字化测试阶段,各个大型试验的工况对于通信载荷测试覆盖性有不同的要求,比如有些工况测试用例需要覆盖高功率放大器后端左右单机、波导、电缆等;而有些工况测试用例需要覆盖通信载荷所有单机、波导、电缆。基于向量化建模结合和多链路冲突检测,可以得到理论所有链路同时工作的所有组合,基于理论上所有组合进行不同批次测试用例数字化编排具有较高应用价值。

3 结论

向量化是处理复杂问题的关键方法之一,向量化一方面可以较大程度减少复杂问题处理过程中的循环遍历次数,显著降低算法复杂度,另一方面可以充分利用高性能计算机处理能力进行高效批处理,进而大幅减小模型运行时间。本文提出的卫星通信载荷向量化建模方法,仅以多项式级别时间复杂度便得到了所有链路理论上所有可能组合,相比传统基于穷举的方法极大提高了建模效率,在数字化设计、批产化制造等阶段具有重要应用价值。