基于最小跳数的星座网络拓扑抗毁性分析

孙景云,张国亭,柳 震,王 进

(1.北京跟踪与通信技术研究所,北京 100094;2.中国航天科工集团第三研究院,北京 100071)

0 引言

单颗卫星对地球的覆盖能力有限,但多颗不同轨道的卫星可组成星座,并通过在卫星节点间建立星间链路实现互联互通,为全球范围内用户提供全覆盖、全实时服务。卫星所处空间环境复杂多变,通信链路易被干扰,当星座网络拓扑中的节点和链路发生随机故障或遭受蓄意损毁,会造成节点受损、链路中断,进而影响星座服务效能。上述故障对网络拓扑结构的变化以及对周围节点和链路的影响,是本文分析研究的重点。

关于网络拓扑结构抗毁性分析,国内外均有相关研究。文献[1]给出抗毁性定义和测度,总结了传统图论中的网络抗毁性指标,如网络韧性度、完整度、连通度等,但上述指标从全局角度出发,未考虑拓扑内部节点与链路直接的关联。文献[2]对比非全连通网络与全连通网络拓扑结构差异,提出基于最短路径数的抗毁性评估算法,以网络中节点之间的最短路径数的长度和条数作为核心考察指标,来评估网络的抗毁性能。网络抗毁性本质在于节点间存在可替代途径,文献[3-4]以网络自然连通度为测度,将复杂网络特征谱与抗毁性建立联系,度量网络抗毁性能。文献[5]提出跳面节点法,根据某一节点到达其他节点的跳数划分跳面,将网络可靠性、抗毁性评估转化为跳面节点可靠性及跳面间关联性进行求解,并给出定量计算的数学解析式。文献[6]将跳面节点法应用到卫星网络中,根据卫星网络高动态、周期性的特点,对跳面节点法进行了改进,提高了对相似拓扑结构的区分度。这些网络拓扑抗毁性模型各有其侧重点,也各有局限性。文献[7]提出区域级网络拓扑抗毁性评估算法,衡量不同区域受到攻击的程度。文献[8]定义了复杂网络冗余度并对网络抗毁性进行量化,通过删除节点评估节点对网络的重要程度。

文献[9]从网络面临的威胁类型出发,可以分为随机失效和蓄意损毁两种失效类型。文献[10]提出无标度网络可以有效应对随机失效带来的影响,而对于蓄意损毁却十分脆弱。因此,研究星座网络拓扑抗毁性,也可以从节点重要性角度来进一步研究[11]。评估节点重要性比较常用的方法有[12]:度中心性,以节点的连接数作为测度指标;接近中心性,以节点靠近网络中心的程度判断节点重要性;介数中心性,以节点/链路作为其中两个节点之间最短路径的桥梁的次数作为刻画节点重要性的指标。

本文以局部网络为分析对象,重点研究网络拓扑中某些节点受损或链路中断对其他节点及网络的影响。对于Walker星座,其网络拓扑对称,度中心性和接近中心性不适用于节点重要性评价指标,介数中心性可以直观描述节点/链路对最短路径数的影响。考虑到卫星发射与维护的高额成本,进行网络拓扑结构抗毁性的分析评估对星座规划设计、运维管控、健康管理均具有重要意义。

1 星座网络拓扑建模

每个卫星设计4条星间链路,包括前后两条同轨卫星链路和左右两条异轨卫星链路。考虑Walker星座,网络拓扑用G表示。星座网络拓扑示意图如图1所示。

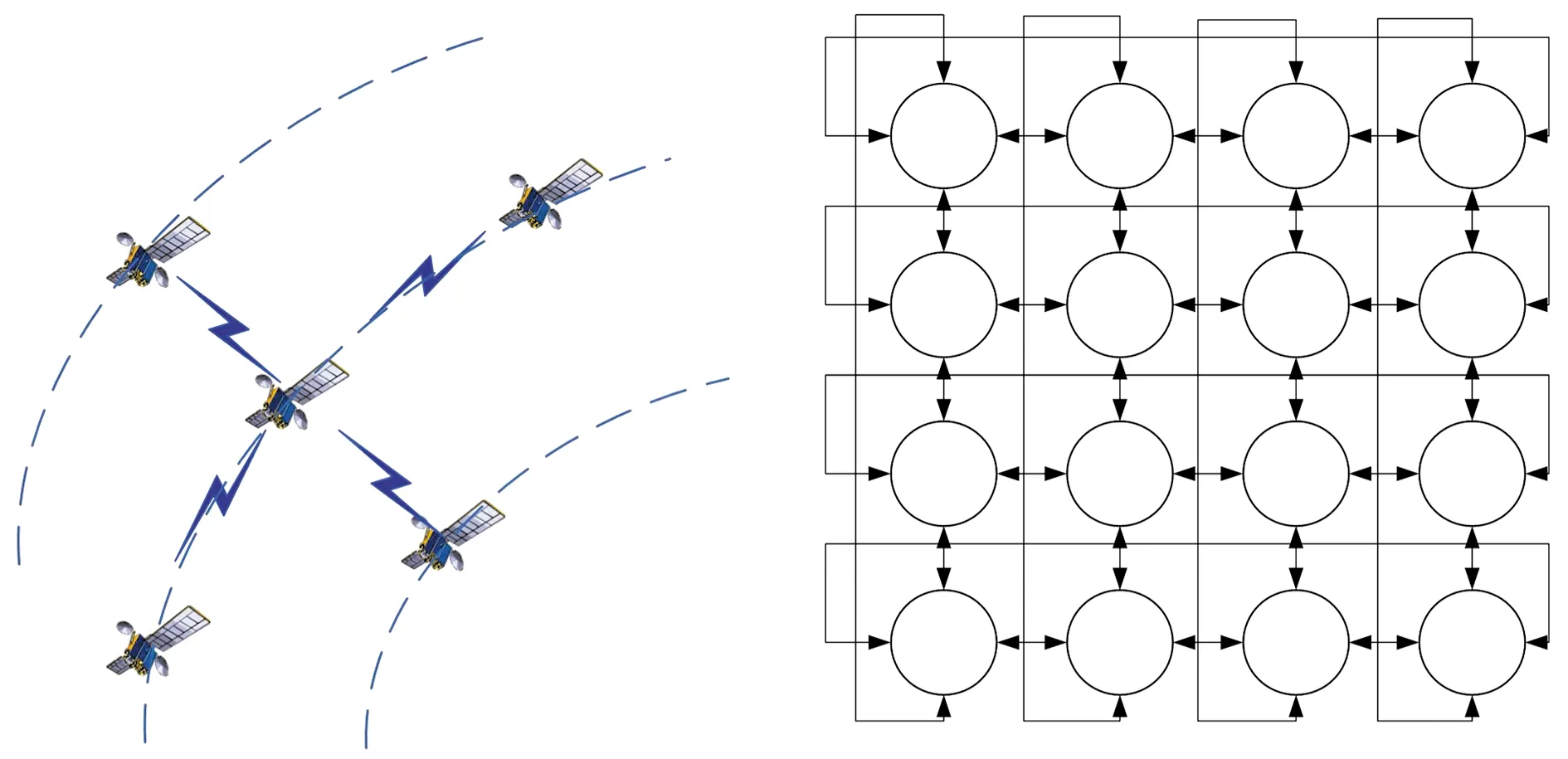
(a) 卫星节点建链关系 (b) 星座网络拓扑图1 星座网络拓扑示意图Fig.1 Constellation network topology diagram

定义1邻接矩阵

以星座中卫星节点作为网络拓扑G中的点,以星间链路作为网络拓扑G中的边,则与网络拓扑G相对应的邻接矩阵A可以表示为:

(1)

式中:Vi(i=1,2,…,N)表示星座中的卫星节点,N为星座中卫星数目,aij表示卫星Vi与Vj之间链路连接情况(i,j=1,2,…,N),aij=1表示链路连通,aij=0则表示链路中断。邻接矩阵A为对称矩阵,由于卫星自身与自身之间不存在星间链路,因此邻接矩阵A的对角元素均为0。

邻接矩阵具有以下性质,可用于判断网络拓扑的连通性和稳健性[13-14]:

性质1设A是N阶图G的邻接矩阵,N≥3,令R=A+A2+…+AN-1,则图G连通的充分必要条件是矩阵R中每个元素均不为零。

2 最小跳数路由算法

每条路径的权值为1时,最短路径算法等效于最小跳数算法。卫星网络拓扑结构呈二维网格状,在异轨和同轨星间链路传播时延相差不大的情况下,可将跳数作为最优路径的主要衡量指标[15]。

从源节点到目的节点,跳数最小时,所有可能经过的节点和链路的集合,定义为最小跳数路由区域。如图2(a),当源节点与目的节点处于同一条轨道面或异轨同一位置时,最小跳数路由区域为一条线;如图2(b),当源节点与目的节点不处于同一条轨道且不同位置时,最小跳数路由区域为一个矩形区域[16]。

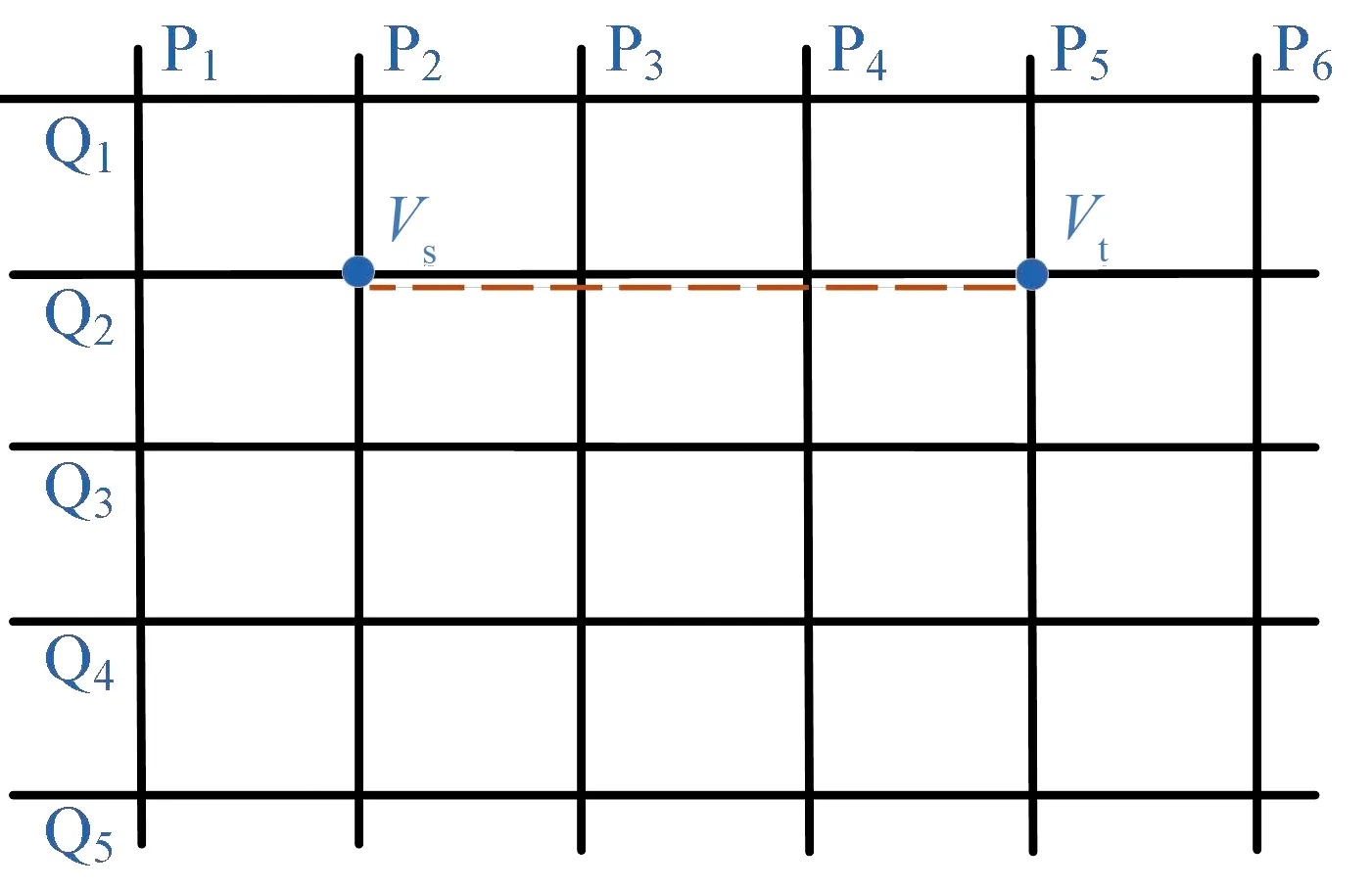
(a) 线形区域

最小跳数可以由最小跳数路由区域中长与宽的和来表示:

K=PD+QD,

(2)

式中:PD(PD≥0)为轨道面距离,QD(QD≥0)为轨道内位置距离。

3 节点/链路重要性分析

定义2节点/链路介数

介数定义为网络中经过某个节点的/链路的最小跳路径数目与网络中最小跳路径总数的比值。节点介数和链路的介数定义分别为[17]:

(3)

式中:σst表示从源节点Vs到目的节点Vt的最小跳路径总数量,σst(Vi)表示从节点Vs～Vt且经过节点Vi的最小跳路径数量,σst(Eij)表示从节点Vs～Vt且经过链路Eij的最小跳路径数量。采用邻接矩阵对节点/链路介数进行计算,得到:

(4)

式中:Kst表示从源节点Vs到目的节点Vt的最小跳数,同理,Ksi表示从节点Vs～Vi的最小跳数,Kit表示从节点Vi～Vt的最小跳数,Kjt表示从节点Vj～Vt的最小跳数。得到:

Kst=Ksi+Kit=Ksi+Kjt+1。

(5)

在最小跳数路由区域中,根据信息流向将流入节点的链路数目定义为入度,将流出节点的链路数目定义为出度,节点(非源节点或目的节点)介数为流入节点的链路介数之和,同时等于流出节点链路介数之和。源节点和目的节点的介数为1。得到如下公式:

(6)

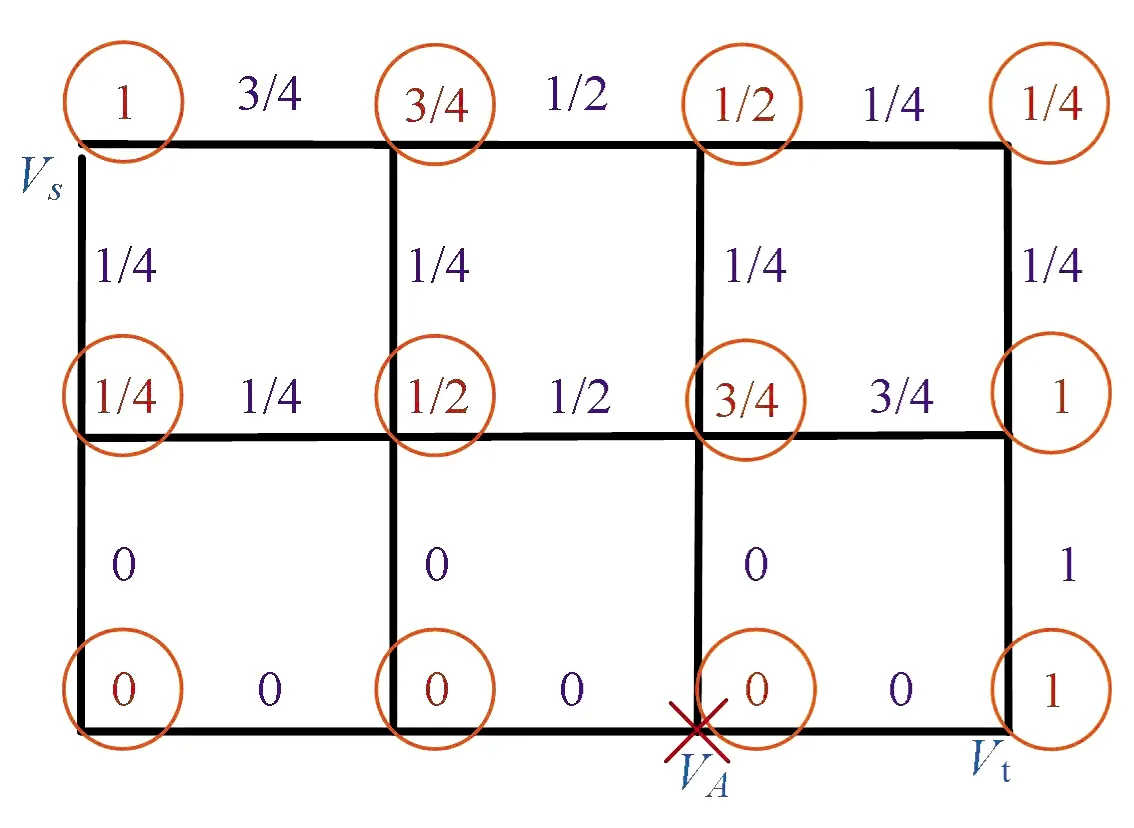
图3为一个3×2(轨道面距离为3,轨道内位置距离为2)的最小跳数路由区域,Vs为源节点,Vt为目的节点,根据介数定义,得到各节点/链路介数。图中,圆圈内数值表示各节点介数,链路旁数值表示各链路介数。考虑某节点受损或链路中断对周围节点和链路的影响。

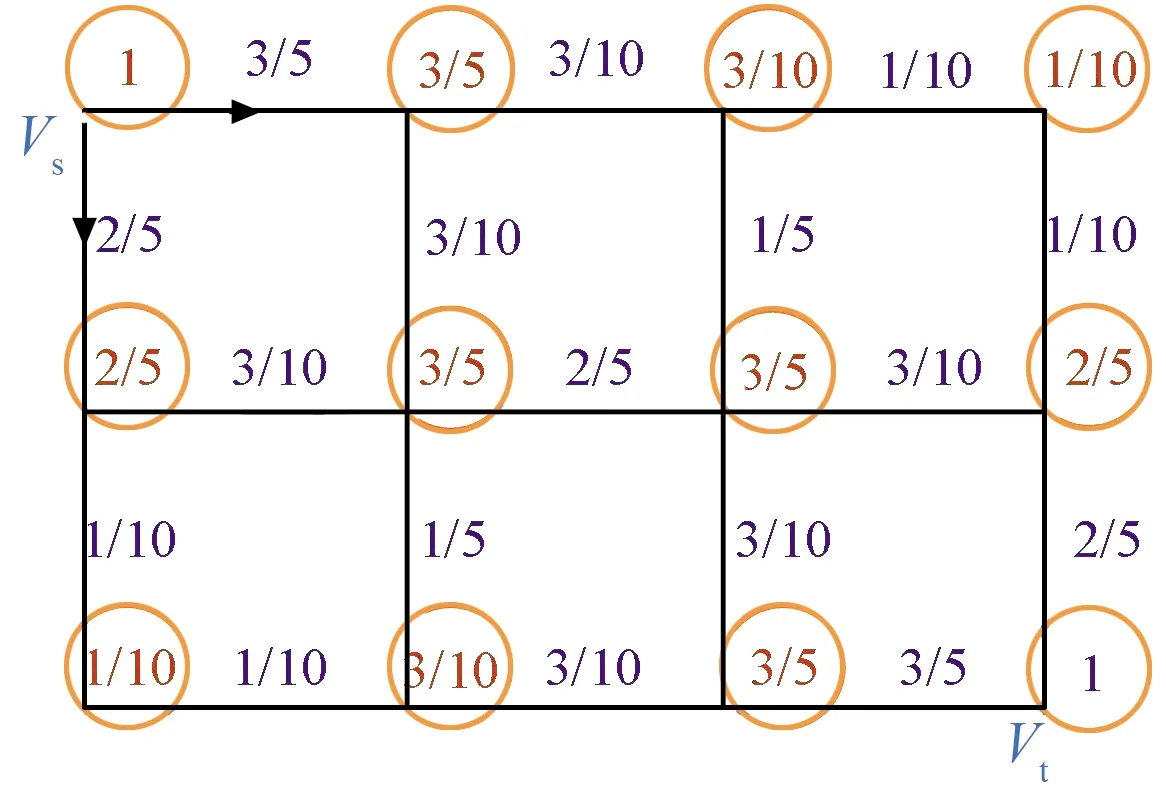
图3 节点/链路介数示意图Fig.3 Node/Link intermediate diagram

推论1若某个节点受损,则与其相连的链路介数为0。

证明:若某个节点损坏,则此节点的介数为0,即WV=0。由式(6)得到:

(7)

推论2若某节点(非源节点或目的节点)流出节点的链路介数和为0,则此节点与流入此节点的链路介数均为0。

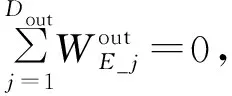
(8)

因此,得到此节点介数为0,且流入节点的链路介数均为0。

4 仿真及结果分析

卫星网络拓扑类似于网格结构,其动态特性主要来自如下几方面:① 卫星节点受损或链路受干扰中断导致星座网络拓扑的改变;② 同轨星间链路比较稳定,而异轨星间链路在靠近极区时因距离、指向角度变化剧烈而中断,又在飞出极区后重新建链;③ 网络中某些节点或链路拥塞导致卫星网络不可用。以上均可归结为节点受损和链路中断两种情况。

4.1 节点受损或链路中断对周围节点/链路的影响

当有节点受损或链路中断时,可根据推论1、推论2正向/反向更新各节点/链路介数。

节点损毁时介数变化示意如图4所示。图中,节点VA受损,根据推论1得到与之相连的链路介数均为0,得到图4(a)介数更新值。流出节点VB的链路介数值为0,根据推论2得到节点VB以及流入VB的链路介数值均为0,同理,可推导出节点VC以及流入VC的链路介数值均为0,介数值更新如图4(b)所示。更新邻接矩阵,根据邻接矩阵性质,得到图4(c)节点和链路的介数值。

(c) 更新路由区域介数值图4 节点损毁时介数变化示意图Fig.4 Intermediate value changing with some nodes damaged

单个节点受损或链路中断,导致周围节点/链路介数值增大;当节点/链路介数值增大到1时,表示所有最小跳路径都要经过此节点/链路,因此,若此节点/链路损毁将导致在当前区域内最小跳路径数为0。

4.2 节点受损或链路中断对网络的影响

考虑随机受损和蓄意损毁两种情况下节点受损或链路中断对网络的影响。其中,随机受损情况下,随机选取网络中节点或链路,设置其状态值;蓄意损毁情况下,根据网络中节点或链路重要程度进行排序[18],优先使重要度高的节点受损或链路中断。以图5网络为例,分析不同情况下节点受损或链路中断对网络的影响。如图5所示路由区域,共有11个轨道面,每个轨道面由6颗卫星组成,卫星编号如图所示,节点1为源节点,节点66为目的节点。根据式(3)计算各个卫星节点介数值,节点2与节点65介数值最大为0.67。

图5 11×6最小跳路由区域示意图Fig.5 11×6 minimum hop routing area

选取不同节点受损,分析对其他节点的影响。如图6所示。节点2(介数值0.67)受损对周围节点介数值影响较大,节点2～11介数值变为0,节点12介数值变为1;节点20(介数值0.045)受损对周围节点影响不大,节点19介数值变化最大,由0.093 1变化为0.055 8。

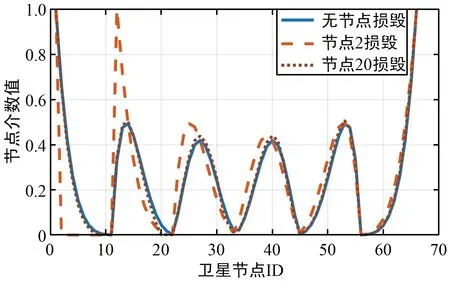
图6 节点受损对其他节点介数值影响Fig.6 Influence of node damage on the intermediate value of other nodes

图7为两种仿真模式下受损卫星数与最小跳路径数变化曲线。蓄意损毁模式下,最少两个卫星节点受损,即导致在当前路由区域中最小跳路径数为0;随机受损模式下,19个卫星节点受损,才使得最小跳路径数为0。

图7 受损卫星数与最小跳路径数变化曲线Fig.7 Number of damaged satellites vs the number of minimum hop paths

图8为两种仿真模式下中断链路数与最小跳路径数变化曲线。蓄意损毁模式下,只需要选择两条链路中断,即导致在当前路由区域中最小跳路径数为0;随机受损模式下,则需要多条链路中断,才能使得最小跳路径数为0。

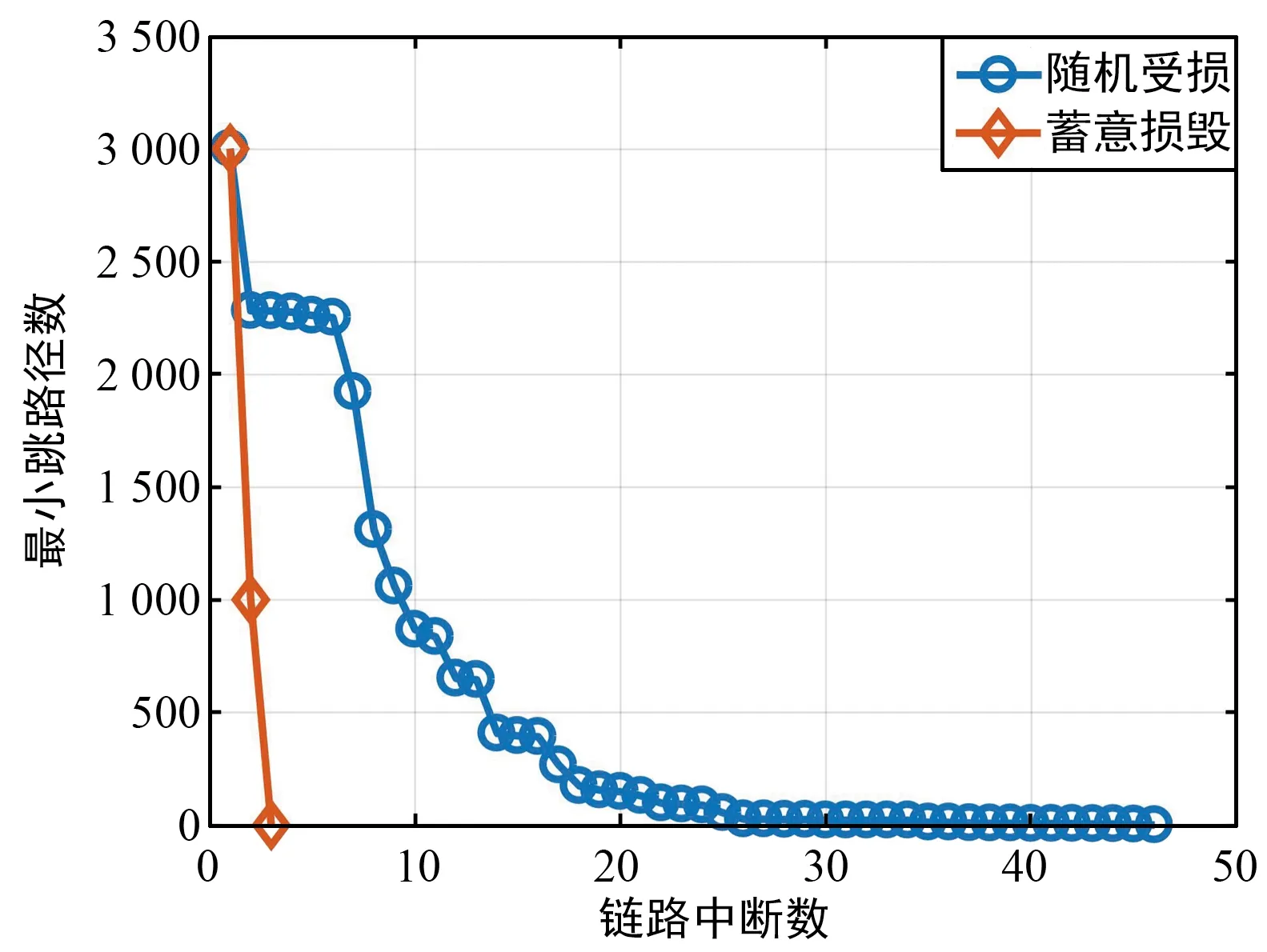
图8 中断链路数与最小跳路径数变化曲线Fig.8 Number of intermediate links vs the number of minimum hop paths

5 结论

本文针对星座网络拓扑呈二维网格特点,基于最小跳数路由算法对星座网络拓扑抗毁性进行了分析。通过邻接矩阵性质计算最小跳路由区域中节点和链路的介数值;通过介数值参数模型给出星座中节点/链路的重要性,并对比分析随机受损和蓄意损毁模式下,部分节点/链路损毁对周围节点的影响。从仿真结果可知,当介数值最大的节点或链路受到蓄意损毁时,网络中源节点到目的节点最小跳路径数会发生急剧变化,这一结果对星座健康管理与运维管控具有实际意义。