基于MGP算法的舰载机回收排序调度技术
崔凯凯, 崔荣伟, 韩 维, 郭 放, 王毓麟, 刘 洁
(1. 海军航空大学航空基础学院, 山东 烟台 264001; 2. 中国人民解放军92942部队, 北京 100161; 3. 军事科学院战争研究院, 北京 100850)
0 引 言
由于舰载机通常采用大机群回收的方式,其在进入最终的着舰下滑道之前必须要根据相应的指标要求进行回收排序,以确定机群中各架舰载机的着舰顺序。因此,对着舰回收排序算法的研究有利于减少舰载机的回收耗时,提高回收任务的效能,保证飞行安全,同时也有利于后续保障和再出动任务的进行。飞机着陆调度(aircraft landing scheduling, ALS)是空中交通管制领域中的一个复杂问题[1],目前相关的研究主要集中在民用航空领域[2-6]。
文献[2]通过序列二次规划确定了高密度运行条件下的最优飞机着陆序列及相应的飞行时间,并基于对排序结果的分析提出了3种排序规则。相关的蒙特卡罗模拟结果表明,通过2次简单的着陆顺序交换,最多可节省17%的燃油消耗。文献[3]基于任务完成总时间最短的目标和滚动时域思想设计了一种结合人工鱼群和粒子群优化(artificial fish particle swarm optimization, AFPSO)的飞机降落排序算法。与先到先服务方法相比,AFPSO算法在单跑道情况下可以使航班队列着陆的总延迟时间减少36%。文献[4]设计了一种用于减小飞机着陆总延迟时间的线性规划方法,该方法通过贪婪式启发算法给出了最大延迟时间上界的估计值,确保了混合整数线性规划模型具有可行解,且该算法采用分枝定界策略对搜索树节点进行了修剪,提高了搜索效率,机场实际数据验算结果表明该算法相对于普通的线性规划算法具有更强的优化能力。文献[5]借助单机调度中的准则选择方法确定了ALS问题中的多个待优化目标函数,并采用包括帝国竞争算法(imperialist competitive algorithm, ICA)在内的多种求解算法对多目标ALS问题进行了求解。仿真计算结果表明,该方法能够有效解决ALS多目标优化问题,在提高航班的准点率和跑道利用率的同时减少了空中交管人员的工作量。文献[6]基于ALS复合分派规则,设计了针对ALS问题的启发式算法。仿真计算结果表明其所提出的算法相较于Lingo软件的求解结果而言,平均每架航班的降落时间可以提前2.4 min。而文献[7]则提出了一种CGIC(costs, generation rule, improvement heuristic, connection rule)启发式算法以解决ALS问题。CGIC基于4种操作规则将ALS问题分解为两个或多个子问题,从而降低了ALS问题的复杂性。仿真结果表明,即使在动态情况下,CGIC依然可以获得高质量的调度求解方案,且计算时间满足实时性要求。
与民航飞机有所不同,舰载机着舰时只有一条着舰跑道可以使用,且跑道的距离远远短于陆基机场,发生逃逸或者复飞的概率要远远大于陆基飞机。同时,舰载机执行的是战斗任务,其在返航时很有可能存在战损,且由于战场形势的多变,作战任务时长可能会超出预期,这将导致返航油量过低的情况。相比于经济效益,航母舰载机在进行回收着舰时更加注重着舰方案是否有利于后续作战和保障任务的高效执行。目前来看,舰载机机群的着舰回收排序主要依靠人工调度实现,即空管人员利用其所掌握的回收机群信息和以往的经验综合进行判断[8]。但采用人工调度的方式不仅增加了航母空管人员的负担,且当待回收的舰载机种类较多、数量规模较大时,该方式难以在短时间内给出高效的着舰方案。此时,空管人员为了保证回收安全,往往采用让剩余油量少的舰载机先行着舰的方式[9],该方式虽然简单易行,但无法从整体上综合考虑机群的着舰回收效能,局限性较大。
因而近年来,部分学者针对舰载机着舰回收调度问题也进行了一定的研究。文献[10]考虑了舰载机回收时的排队特性以及着舰失败的可能,对舰载机的着舰回收调度问题进行了分析。文献[11]针对舰载机回收时甲板跑道容量受限问题,比较了先到先服务、依据最早到达时间、滑动时间窗口等3种算法的回收排序效果。仿真结果显示滑动时间窗口排序法计算量较小且具有较好的优化效果,但文献中所用的排序算法均利用了舰载机的预计到达时间,难以适用于舰载机大机群到达的情况[12]。文献[13]针对典型的舰载机回收模式提出了一种考虑着舰失败架次饱和度的回收调度策略,解决了着舰失败队列与首次着舰待机队列之间可能出现的资源点争夺问题。文献[11,13]所提到的几种排序算法以及空管人员所使用的“油少先着舰”排序方式本质上都属于启发式算法,此类算法具有快速的响应能力,但求解效果受主观确定的启发式规则的影响较大,且不能够进行迭代优化。文献[14]针对机群着舰回收排序问题,提出了一种基于蚁群算法的动态排序算法,使舰载机机群能够以最优顺序着舰。通过与最少燃料优先服务的方法和静态蚁群排序算法相比较,验证了基于蚁群算法的动态排序算法的优势。文献[15]综合考虑了着舰返航时舰载机的剩余油量、战损情况等随机性因素的影响,建立了相应的着舰回收模型,用于对回收着舰的风险成本进行优化,并提出了一种带有模拟退火机制的粒子群算法以对着舰回收排序问题进行求解。文献[16]将舰载机着舰回收调度问题抽象为随机规划问题,并提出了一种基于着舰优先序指标的蒙特卡罗-差分进化实时排序调度算法。仿真结果显示在相同的初始条件下,利用蒙特卡罗-差分进化算法求解得到的目标函数值呈现出了较好的统计特性,且算法的收敛速度较快。文献[12]针对舰载机着舰回收调度问题,构造了一种考虑加权完成时间的目标函数,并设计了一种经过改进的人工蜂群算法对该问题进行求解,经仿真对比验证了其所提出的算法具备较强的优化能力和鲁棒性。
上述研究很少考虑空中加油对着舰方案的影响,使得其对返航舰载机油量有着较大的限制,适用场景相对受限。且上述调度求解方法从本质上而言大多属于元启发式算法,而元启发式算法在迭代求解的过程中需要进行大量的随机搜索操作,当问题规模较大时,其搜索效率和搜索稳定性会变差[17]。
针对启发式算法以及元启发式算法的不足,文献[18]提出了超启发式算法的概念,超启发式算法的提出为复杂调度问题提供了一种新的求解思路。该算法通过高层次的启发式策略来操纵若干个低层次启发式方法,从而生成新的寻优算法,超参少且实用性较强[19],在近年来引起了广泛的关注。其已被用于求解航母甲板作业调度[20]、自动化码头箱位分配[21]、车辆取送货路径规划[22]以及云计算调度[23]等众多工程实践领域,取得了理想的效果。进一步,学者们将遗传算法的优化过程模拟到超启发式算法上,形成了遗传规划(genetic programming, GP)算法[24],并将其广泛应用于项目调度问题。文献[25]首次将超启发式调度算法应用于具有随机工时的项目调度问题中,提出一种超启发式集成遗传规划方法,通过进化优先级规则组合来求解随机资源受限的项目调度问题。该算法通过3种不同的局部搜索方法来增加各代种群的多样性。此外,算法还设计了一种序列投票机制来处理随机资源受限的项目调度过程中的协同决策问题,仿真验证表明该算法相对于启发式、元启发式和单一超启发式算法具有一定的优势。文献[26]提出一种基于遗传规划的动态车间调度算法,对最长完工时间和平均延迟时间进行了优化,并借助排序规则的自动生成机制,提高了车间调度算法在不同场景中的动态适应性。文献[27]针对多技能资源约束项目调度问题提出了一种遗传规划超启发式算法,其通过使用单个任务序列向量进行编码,并基于修复的解码方式来生成可行的调度方案,仿真对比实验验证了该算法在求解效果和收敛速度方面的优势。除此之外,GP算法在其他一些项目调度问题中也获得了良好的效果[28-30]。但目前尚未见有利用超启发式算法对着舰回收调度问题进行求解的相关文献。
针对当前舰载机着舰回收调度问题研究过程中存在的不足,本文建立了考虑空中加油条件的舰载机机群着舰回收调度问题模型,同时基于超启发式思想设计了一种带强制着舰规则的GP (GP with mandatory landing rules, MGP)算法,用于对着舰回收排序问题进行求解。
1 舰载机机群回收排序问题模型
1.1 舰载机着舰回收排序问题分析
通常而言,舰载机返航的过程可分为4个阶段,即引导段、待机段、进场段和着舰段[31]。在通常情况下,当舰载机飞行至距航母200 n mile的位置后,舰上的航管中心开始接管舰载机。
一般情况下,根据不同的天气状况及昼夜情况,固定翼舰载机的回收着舰模式可分为3类。其中,第一类回收着舰模式要求昼间天气状况良好,能见度大于5 km,此时可采用目视进场以及人工着舰的方式;当航母上方云层的遮挡范围大于5/8时,一般采用第二类回收着舰模式,即采用仪表引导系统进场,并利用自动着舰系统进行着舰;当航母上空300 m以上有云层或夜间着舰时,通常采用第三类回收着舰模式。可见,第三类回收方式适用于夜间和恶劣气象条件下的着舰回收任务,因此本文以第三类回收着舰模式为例研究舰载机的回收排序问题。
第三类回收着舰模式的飞行航线如图1所示。通常情况下,在航母左侧距离航母约20 n mile的位置设置马歇尔等待航线,即在1 800 m以上的空域按照300 m的高度差设计多层等待航线。相邻马歇尔等待航线之间的水平间隔为1 n mile。在未接到着舰指令时,舰载机在马歇尔等待航线上盘旋飞行,当接到着舰许可指令后,舰载机从等待航线偏离点A处离开当前等待航线,并以20 m/s的下滑速度经过最底层等待航线的脱离点B(马歇尔点)后飞至进场始发点C,之后以10 m/s的下滑速度左盘旋飞行,当飞至舰尾后方约10 n mile的位置D时,飞机的高度降至365 m,飞机转入平飞状态,直至飞到舰尾后方3 n mile处的E点时,自动着舰系统开始工作,舰载机进行下滑着舰飞行。如出现逃逸或复飞的情况,舰载机需要再次爬升至365 m的高度,之后按照复飞航线飞行并再次进行着舰。

图1 第三类回收着舰模式下的飞行航线图Fig.1 Flight route map under the third type of carrier landing recovery mode
1.2 机群回收约束条件分析
为了保证机群的安全,舰载机在进行回收排序的过程中,会面临许多限制条件,本节将对该问题所涉及的限制条件逐个进行分析。
1.2.1 完整度约束条件
舰载机在执行作战任务的过程中,经常会出现一定程度的损伤,若损伤情况较为严重,则可能会影响舰载机的正常飞行或操纵。当出现舰载机无法稳定飞行或不能正常操纵舰载机的情况时,通常需要联系陆基机场进行降落,但当航母舰队执行远海作战任务且在舰载机航程内无可用的陆基机场时,只能在航母甲板上进行紧急降落。在紧急降落时,需要将跑道附近的舰载机迅速转运至安全区域,并架起尼龙阻拦网,待故障机抛掉其所搭载的武器燃料后实施紧急着舰。在故障机完成着舰后,甲板上的人员还要针对可能出现的突发状况进行灭活和人员救助等工作。由此可见,若将无法正常着舰的故障机安排在着舰回收序列中,会使机群着舰的连续性受到较大影响。因此,通常的处理方式是:① 若故障机具备空中逗留能力,则先让其在空中盘旋等待,待其他正常机完成着舰后再安排故障机进行着舰;② 若故障机无法在空中稳定飞行,则将其安排在大机群之前进行着舰。
本文中,用完整度WZi表示舰载机i的受损程度。完整度越高,表示受损程度越小,且只有当完整度满足一定的条件时,才能将其安排进着舰序列中,即WZi>WZmin。本文中,取WZmin=60%。
1.2.2 剩余油量约束条件
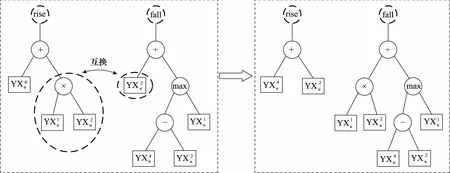
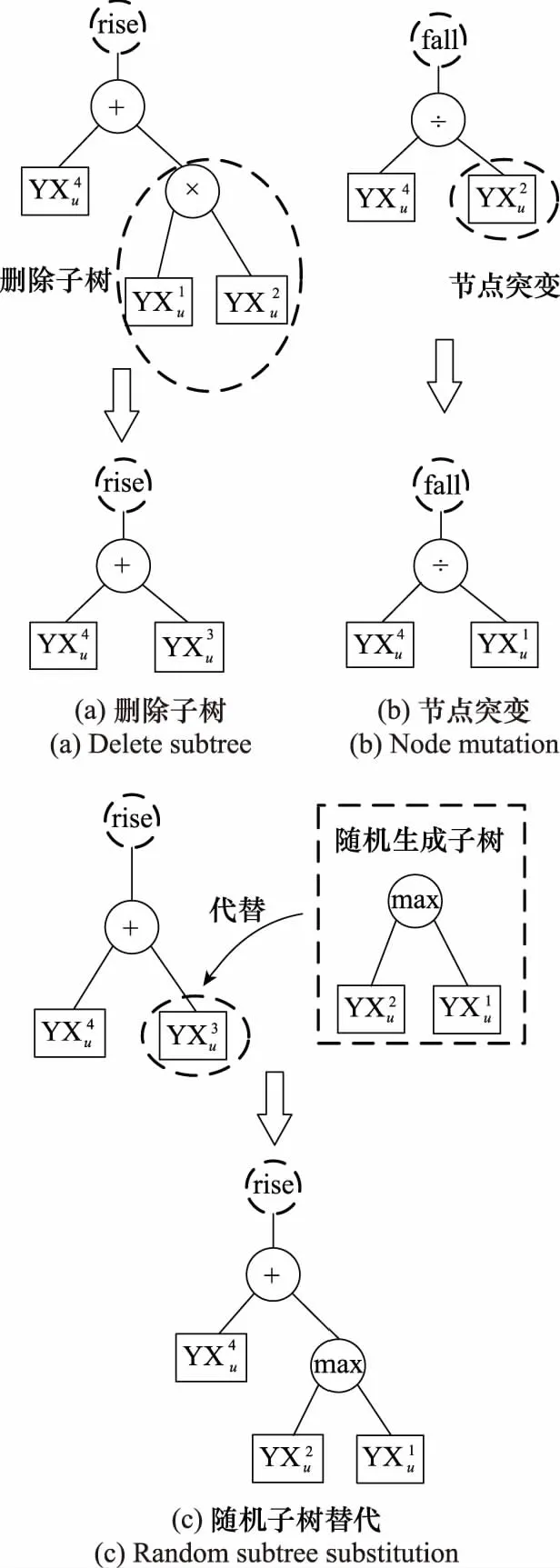
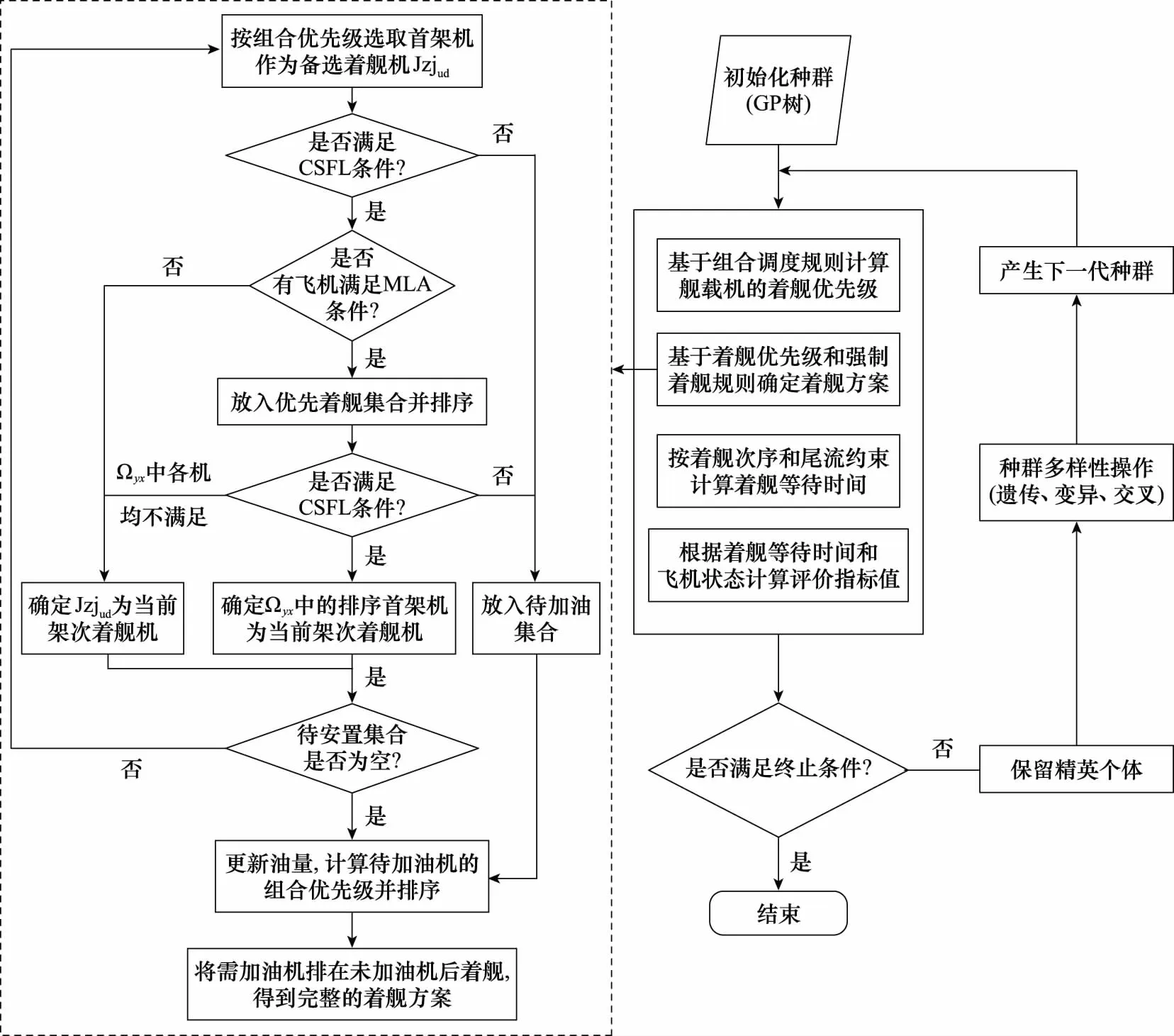
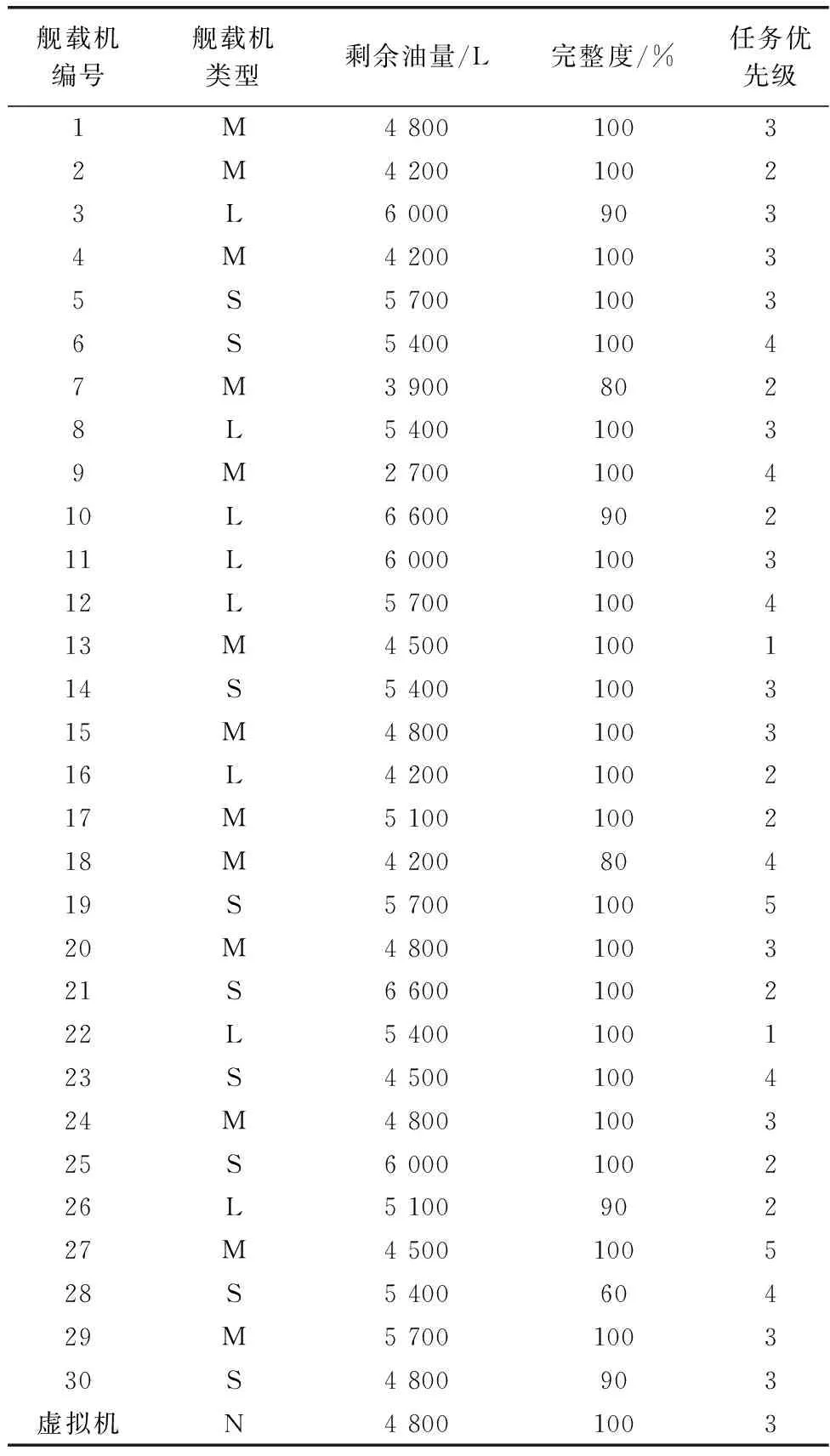
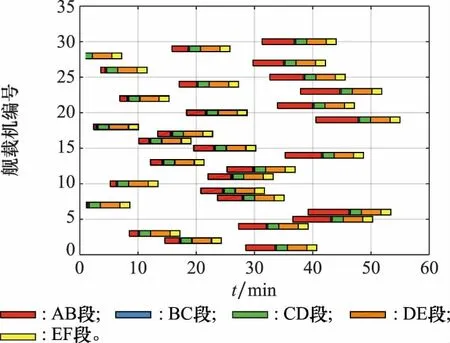
受舰载机起落架以及阻拦索承载能力的限制,舰载机在进行着舰时通常面临最大油量限制,即着舰载机i在其着舰时刻的剩余油量Ozj,i必须小于最大允许着舰油量Omax。同时,由于舰载机在着舰过程中无法保证一次着舰成功,且当前序飞机在着舰失败后进行二次着舰时有可能会占据后续飞机的航线。因此,在初始的着舰方案中,Ozj,i均应大于某一最小安全裕度值Osafe。当着舰方案生成后,由于着舰队列内可能会出现复飞或者逃逸的情况,这将会导致后续舰载机的实际着舰时刻较原有着舰方案有所推迟,但无论如何应保证舰载机在进行着舰时,其剩余油量大于最小极限油量Omin。若经判断当前飞机i的Ozj,i Osafe=Off+Ocr+Omin (1) 式中:Off、Ocr分别表示最长复飞航线所需油耗和前序某一架次飞机复飞可能给后续飞机带来的额外最大油耗。按照式(1)选取Osafe的实际意义在于:初始着舰方案中的飞机在不依赖空中加油的条件下,当前序飞机中出现一次着舰失败并重新着舰后,该架次飞机仍有一次着舰失败并重新着舰的机会,且其剩余油量可以保证舰载机在二次着舰仍然失败后可以安全抵达空中加油位置,而不会出现油量耗尽的情况。考虑到机群回收过程涉及到多种机型,且各机型的油耗速率不同,式(1)中的变量数值与飞机机型直接相关。为了便于处理,后续将剩余燃油油量转换为剩余燃油可用时间来进行处理。相应地,Omin、Omax、Osafe、Off、Ocr可转换为TOmin、TOmax、TOsafe、TOff、TOcr,即在后续的研究中,用剩余燃油可用时间来描述舰载机的剩余油量约束条件。记TOi为舰载机i在初始时刻的剩余燃油可用时间,则有: (2) 式中:Oi表示舰载机i在初始时刻的剩余油量;yhi表示舰载机i的耗油率,其具体数值与舰载机的类型有关。 1.2.3 尾流间隔时间约束条件 舰载机在进行顺序着舰的过程中,为了避免由前序舰载机i所产生的飞行尾流对后续飞机j的影响,相邻两架飞机经过航线上相同位置的时间必须满足一定的间隔要求,这一限制即尾流间隔时间限制。一般情况下,尾流间隔时间的限制要求与前后两架次飞机的类型有关,表1给出了不同类型飞机之间的尾流间隔时间限制要求[8]。 表1 尾流间隔时间限制Table 1 Wake interval time limit 表1中的S、M和L分别表示小型、中型和大型舰载机。在实际着舰过程中,当前续飞机完成着舰后,甲板上的工作人员需要进行跑道清空以及阻拦索复位的工作。在此期间,不允许其他舰载机进行着舰,但由于跑道清空的时间一般要小于舰载机尾流间隔时间限制[16],所以可认为该约束已包含于尾流间隔约束中,而无需再进行单独考虑。 第1.2节对舰载机机群回收排序问题中的约束条件进行了分析,本节基于前述分析,建立了基于舰载机完整度、任务优先级、剩余油量飞行时间、回收等待时间以及空中加油次数的回收排序调度评价指标。下面对上述因素展开分析。 (1) 剩余油量飞行时间 基于第1.2节中的分析可知,在舰载机进行着舰时,其剩余油量必须满足一定的限制,设有n架舰载机需要进行回收,则在回收起始时刻,各架舰载机的剩余油量可飞行时间应满足TOsafe+TML (3) 式中:j=1,2,…,n,表示舰载机的编号。由式(3)可知,舰载机的剩余油量可飞行时间越短,其着舰的紧迫度越高。 (2) 舰载机完整度 基于第1.2节中的分析可知,各架舰载机在参与回收时,其完整度必须满足WZi>WZmin,i=1,2,…,n。与剩余油量可飞行时间类似,当舰载机的受损情况较为严重(即舰载机的完整度较小)时,其所对应的着舰紧迫度较高。所以,由WZi所决定的第i架舰载机的着舰紧迫度可表示为 (4) (3) 后续任务优先级 当舰载机完成回收任务后,一般需要进行机务检查和保障,以使其快速恢复作战能力并等待下次出动。同时,当前波次返回的舰载机在后续阶段可能需要执行不同的任务,而这些任务的紧迫程度往往也存在差异。这里将舰载机后续任务的紧迫程度用优先级YXJi来表示,其中YXJi的取值为1~5的整数,且取值越小,表示任务的紧迫程度越高,YXJi的具体数值可提前由舰面调度指挥人员根据任务的执行需求情况给出。考虑YXJi对着舰回收排序方案的影响,要求后续任务优先级高的舰载机尽量先着舰。基于此,可以给出由YXJi所决定的第i架舰载机的着舰紧迫度: (5) (4) 回收等待时间 在舰载机机群进行回收着舰的过程中,舰载机在着舰前的等待时间DTi是一项极为重要的指标。严格来讲,舰载机的等待时间应记为从其进入返航待机区开始到完成着舰的时间,但这样一来,就需要考虑舰载机从进入返航等待区到进入相应的马歇尔等待航线的具体路线,这一过程的随机性较大,且不属于本文的研究范畴。进一步,考虑到机群返回时各架飞机进入返航区的时间差异较小,这里为了简化问题,以首架着舰机经过马歇尔点的时刻T0为计时起点,计算舰载机的等待时间,即DTi=ZTi-T0。其中,ZTi表示第i架舰载机的着舰时刻。 基于上述指标影响因素,设计如下回收着舰排序评价指标: (6) (5) 空中加油次数 虽然在剩余油量飞行时间部分已经对舰载机的油量进行了一定的限制,但是上述限制并不能保证每一架飞机都能够实现安全油量着舰,尤其是在机群规模较大或舰载机剩余油量普遍较少的情况下。此时,在生成着舰排序方案时,就极有可能出现部分舰载机燃油不足,无法实现安全油量着舰的情况。在不考虑前序飞机着舰失败的情况下,若着舰方案中仍有舰载机无法实现安全油量着舰,则需要在着舰方案执行的同时安排油量不足的舰载机进行空中加油,待空中加油完毕后令其重新返回着舰序列,待未加油的舰载机完成着舰后再进行着舰。 (7) 式中:nkj表示在着舰方案中需要进行空中加油的舰载机数量。 基于第1.2节和第1.3节的分析,可以将舰载机机群回收着舰排序调度问题概括为在保证飞行安全的前提下,通过合理安排舰载机的着舰顺序,使得着舰排序评价指标式(7)尽可能小。其决策变量可以用混合整数规划(mixed integer programming, MIP)模型表示如下: (8) 为了表达方便,式(8)中引入了编号i=0的虚拟机Jzj0,该虚拟机作为着舰序列的首架机,且真实飞机k在虚拟机后的安全尾流间隔时间WLT0,k均相同,具体数值WLT0为 (9) 借助式(8)可以将舰载机机群回收调度问题的数学模型表示为 MinJ(xi,j)= (10) (11) TOsafe+DTi (12) TOmin (13) xi,j=0,i∈N1;j∈N0 (14) minDTi≥JTmin+TML,i∈N1 (15) (16) (17) 其中,式(11)表示着舰方案中前后两架相邻的舰载机之间要满足尾流安全要求;式(12)表示在不进行空中加油的舰载机集合N0中,所有的舰载机都必须满足安全油量着舰的要求;式(13)表示在着舰方案中,只有当舰载机无法实现安全油量着舰的情况下才会进行空中加油,且在着舰方案开始时刻,在需要进行空中加油的舰载机集合N1中,舰载机都必须有充足油量以满足空中加油航线的需求;式(14)表示在着舰方案中需要进行空中加油的舰载机在完成加油后需排在未加油的舰载机之后进行着舰;式(15)表示进行空中加油的舰载机着舰等待时间大于马歇尔点至着舰点的飞行时间与完成空中加油的时间之和。其中,JTmin表示完成空中加油任务的最短耗时;式(16)表示除了虚拟机,每架飞机紧邻的前序飞机有且只有一架;式(17)表示包括虚拟机在内,每架飞机紧邻的后续飞机不多于一架(即最后着舰的飞机后续无紧邻飞机)。 舰载机机群回收调度从本质上而言属于作业车间调度问题(job shop scheduling problem, JSSP),当返航舰载机数量为n时,共有n!种方案可供选择,当舰载机数量较多时,很难采用枚举法求得最佳的着舰方案。当前,针对JSSP的求解方法主要有启发式算法和元启发算法,启发式算法通过制定启发式优先规则可以快速生成调度方案,计算效率高,但是由于在规则制定过程中存在较大的主观性,且算法过于贪婪,容易陷入局部最优解,导致其最终的优化效果无法保证。元启发式算法将调度方案映射为某些特定的对象(如生物群中的个体或多维抽象空间中的微粒),并通过模拟自然界的某些过程或生物的群体行为对最优个体进行搜索,具备一定的跳出局部最优解的能力,但是在寻优过程中,存在大量的随机搜索行为,当问题规模增大时,其搜索效率较低。 超启发式算法的主要思想是通过某种高层管理策略对一系列底层的启发式算法进行处理和操纵。GP算法作为超启发式算法的一种,实际上就是通过上层的遗传算法操作规则对底层的调度优先规则进行重新整合,以生成最优的组合优先规则,用于产生调度方案的算法。与以遗传算法(genetic algorithm, GA)为代表的元启发式算法相比,其给出的结果是用于求解调度问题的调度规则,而不是针对特定问题的某一调度方案。GP算法解决了纯启发式算法不具备优化功能的问题,当问题规模较大时,其在搜索空间和搜索效率方面均具备明显优势。 GP算法可以通过底层的启发式规则不断生成新的组合调度优先级规则,并对组合规则进行迭代优化,且调度优先规则通常可以用一个调度优先级函数来表示。因此,对调度规则的优化等同于对优先级函数的优化。在应用GP算法之前,首先需要确定底层的启发式调度规则,针对舰载机机群的回收排序问题,本文选择以下4种启发式调度规则: (1) 油少先着舰规则,相应的优先级函数为YX1=TO; (2) 优先级高先着舰规则,相应的优先级函数为YX2=YXJ; (3) 完整度低先着舰规则,相应的优先级函数为YX3=WZD; (4) 与前序舰载机尾流间隔要求短的机型先着舰规则,相应的优先级函数YX4=WLJ。 由于在后续的遗传规划操作中需要对上述启发式规则所对应的优先级函数进行相应的加减乘除或极值运算,为了避免优先级函数量级不同对计算结果的影响,此处对优先级函数的数值进行了归一化处理: (18) 与GA类似,在利用GP算法进行调度方案求解时,也需要对种群中的个体进行编码。但有所不同的是,GP算法中的个体是一种由底层调度优先规则所构成的组合调度规则,其不同的个体可以用不同的GP树来表示。如图2所示,GP树是一种由计算符节点和终端规则函数节点所组成的一种树状结构。图2中,虚线圆节点表示深度为0的顺序判断编码[25],rise(升序)表示组合优先级函数的值越大,优先级越高;fall(降序)表示组合优先级函数的值越小,优先级越高。圆节点表示计算符节点(也可称为根节点),这里选择+,-,×,÷,max,min这6种计算符形式。矩形节点为终端规则函数节点(也可称为叶节点),可从第2.1节中所设计的4种归一化优先级函数中进行选择。 图2 GP树调度规则编码结构Fig.2 GP tree scheduling rule coding structure 图2中给出的两个GP树的深度均为4,即GP树中第4层中的节点均为叶节点。在进行GP树种群初始化时,为了保证种群的多样性,通常不希望事先指定GP树的具体层数和结构。因此,这里只对GP树的深度进行限制。考虑到机群回收排序问题中终端优先级规则函数的可选数量,这里将GP树的最大深度限制为Lmax=4,同时为了保证最终的组合调度规则中至少含有两个终端规则函数,GP树的最小深度Lmin=2。GP树个体的生成过程可分为以下两个步骤。 步骤 1确定2Lmax-1个节点的类型,首先,将第Lmax层的所有节点确定为叶节点;进一步,将剩余的节点随机确定为根节点或叶节点,得到“满节点数”的GP树个体;最后,对叶节点下层所连接的节点结构予以删除,确保叶节点上层所连接的节点全部为根节点。 重复步骤1和步骤2共Npop次,便可得到种群规模为Npop的初始GP树种群。 在获得初始的GP树种群后,需要确定种群中各个个体的适应度值,以便进行后续的遗传操作。与传统的遗传算法不同,GP树个体只对应于某种组合调度规则,而并非直接对应于某种特定的调度方案,因而在对GP树的适应度进行计算之前应先确定GP树规则所对应的调度方案。如图2所示,GP树所对应的组合调度规则可表示为 (19) 即需要根据式(19)所给出的组合调度规则生成相应的着舰回收调度方案,在介绍调度方案生成算法之前,需要引入当前安全油量着舰(current safe fuel landing, CSFL)和强制提前着舰(mandatory landing ahead, MLA)两个判断性条件。 (1) CSFL条件 CSFL条件是指在着舰方案设计过程中,当前序着舰序列已确定,而在选择某架舰载机作为下一架次着舰机时,被选中的舰载机到达着舰点时的剩余油量应大于安全着舰油量Osafe。转化为剩余油量飞行时间,可将CSFL条件表示为 DTj+WLJj,i (20) 式中:i表示被选中的当前飞机编号;Ωzj表示已安排着舰次序的舰载机集合;Ωust表示尚未确定着舰次序的舰载机集合。 (2) MLA条件 MLA条件是指在着舰方案设计过程中,若按照一定规则选取某架舰载机j作为当前着舰机,则未安排着舰次序的舰载机i必然无法实现安全油量着舰,为避免空中加油情况的出现,在条件允许的情况下需要将i的着舰次序提前,即满足: DTj+WLJj,i>TOi-TOsafe,i,j∈Ωust (21) 在满足式(21)时,需要考虑将i的着舰次序提前。 下面借助CSFL条件和MLA条件,给出基于组合调度规则生成着舰回收排序方案的算法步骤如下。 步骤 1首先选择虚拟机Jzj0作为着舰方案中的首架机,并设置其虚拟着舰等待时间DT0=TML-WLT0(因所有真实飞机与虚拟机之间的尾流安全间隔时间均为WLT0,所以着舰方案中在虚拟机之后的首架飞机的着舰等待时间为TML)。令待安置集合Ωust=Ωall,其中,Ωall表示全部待回收舰载机的集合; 步骤 2按照GP树中的组合调度规则,计算集合Ωust中各架舰载机的组合优先级函数值,然后将组合优先级函数值按照[rise]或[fall]规则进行排序; 步骤 3选择排序最靠前的舰载机作为待选着舰机Jzjud。首先,计算将Jzjud安排在当前架次是否满足CSFL条件,若不满足,则判定Jzjud需要进行空中加油,并将其从集合Ωust转移到待加油集合Ωjy中,按照排序结果选择下一位次的舰载机作为新的Jzjud。重复此操作,直至新的Jzjud满足CSFL条件; 步骤 4将Jzjud暂定为当前架次的着舰机,判断Ωust中的各架飞机是否满足MLA条件。若满足,则将相应的飞机放入到优先着舰集合Ωyx中;判断Ωyx是否为空集,若Ωyx为空集,则将Jzjud正式确定为当前架次的着舰机Jzjc,转至步骤6;若Ωyx不为空集,则转至步骤5; 步骤 5将Ωyx中的舰载机按组合优先级函数值进行排序,按顺序依次判断其是否满足CSFL条件,若不满足则将其放入到集合Ωjy中,若满足则将其直接确定为当前架次着舰机Jzjc;若集合Ωyx中的舰载机均不满足安全油量着舰条件,则将Jzjud正式确定为当前架次的着舰机Jzjc; 步骤 6将当前架次的着舰机放入到着舰集合Ωzj中,并根据前一架次的着舰等待时间以及尾流间隔时间要求确定当前架次着舰机Jzjc的着舰等待时间DTc,更新Ωyx=Ø,更新待安置集合Ωust=Ωall-Ωjy-Ωzj; 上述着舰调度方案生成过程中,在步骤4~步骤5中引入了强制着舰规则,尽可能避免了舰载机出现空中加油的情况。为了更清楚地展现算法的逻辑结构,带强制着舰规则的回收排序调度方案生成算法如算法1所示。 算法1 带强制着舰规则的回收排序调度方案生成算法输入 GP树个体,Ωall中各架飞机的状态信息输出 舰载机机群回收着舰排序方案1 初始化:确定虚拟机Jzj0为首架着舰机,DT0=TML-WLT0,Ωust=Ωall。确定Ωust中所有飞机的YXiu,i=1,2,3,42 While Ωust=Ø then 3 根据GP树编码计算Ωust中个飞机的组合优先级函数,并按[rise]或[fall]规则排序,选择序列中的首架机为Jzjud 4 While Jzjud不满足CSFL条件 then 5 将Jzjud从Ωust转移到集合Ωjy 6 选择序列中下一架飞机作为Jzjud 7 end 8 for Jzji in Ωust do 9 if Jzji满足MLA条件 then 10 将Jzji放入集合Ωyx 11 end 12 计算Ωyx中各架舰载机的组合优先级函数,并按[rise]或[fall]规则排序,得到序列XLyx 13 for Jzji in XLyx do 14 if Jzji 满足CSFL条件 then 15 确定Jzji为当前架次着舰机Jzjc 16 else 17 将Jzji放入集合Ωjy 18 end 19 end 20 if Ωyx中没有舰载机满足CSFL条件 THEN 21 将Jzjud作为当前架次的着舰机Jzjc 22 end 23 end 24 将当前架次的着舰机Jzjc放入集合Ωzj,更新着舰序列XLzj=[XLzj;Jzjc] 25 更新Ωyx=Ø,Ωust=Ωall-Ωjy-Ωzj26 end27 将Ωjy中的舰载机的油量更新为maxj=1,2,…,nTOj28 计算Ωjy中各架舰载机的组合优先级函数,并按[rise]或[fall]规则排序,得到序列XLjy29 更新XLzj=[XLzj;XLjy] 与普通的GA类似,在GP算法中,为了保证种群的多样性,对GP树种群引入了遗传、交叉和变异3种形式的遗传操作,遗传操作主要是为了选出合适的GP树个体作为父代进行遗传操作。此处,为了选择适应度值相对较优的个体作为父代进行遗传操作,采用二元锦标赛模式对父代个体进行选取,即“两两比较,择优选择”。交叉操作即选择两个不同的父代个体,随机选择其中的某一节点连同其全部的子节点进行交换,从而得到新的子代个体,如图3所示。 图3 GP树交叉操作示意图Fig.3 Schematic diagram of GP tree crossing operation 本文选取3种变异操作模式,如图4所示。第1种为删除子树操作,选择GP树中的某一根节点及其全部子节点进行删除,并随机生成一个叶节点用于代替原根节点的位置;第2种变异操作为节点突变,选择GP树中的任意节点,对这一节点中的取值进行修改,而节点类型不变;第3种操作为随机子树替代,任选一个节点,用随机生成子树代替该节点,从而得到新的子代个体。 图4 GP树变异操作示意图Fig.4 GP tree mutation operation schematic diagram 3种不同的变异方式可以通过对其设置相应的发生概率予以控制,进一步在进化的过程中引入精英个体保留策略,以保证适应度最优的GP树个体可以保留到下一代种群中。图5给出了本节所建立的基于MGP的舰载机机群回收排序算法的框架图。 图5 基于MGP的舰载机机群回收排序调度算法框架Fig.5 Framework for carrier aircraft fleet recovery sequencing scheduling algorithm based on MGP 在仿真过程中,设置MGP算法中的种群数量为100,最大迭代次数为80,个体变异概率为0.2,顶点变异概率为0.5,假设待回收机群共有30架飞机,各架飞机的初始状态信息如表2(部分信息参考文献[8])所示。 表2 待回收机群的初始状态信息Table 2 Initial status information of the carrier aircraft fleet to be recovered 在仿真过程中,假设S、M、L、N型飞机的油耗速率分别为0.6 L/s、0.9 L/s、1.2 L/s、0.6 L/s,在仿真过程中有关的时间常数项取值如表3所示,不同机型间的尾流安全间隔时间在表1中已经给出。 表3 仿真中时间常数变量的取值Table 3 Value of time constant variable used in simulation 利用本文所设计的MGP算法对表2中需要回收的机群进行着舰排序,所得到的排序结果如表4所示。从表4可以看出,其着舰安全时间裕度均大于0 s,即在此着舰方案中需要进行空中加油的舰载机数量为0架。最终所得到的评价指标函数值为19 570 s,着舰回收任务的完成时间为3 299 s,算法的计算求解时间为16.4 s。 表4 着舰排序方案结果Table 4 Landing sequencing scheme results 续表4Continued Table 4 为了展示着舰方案中不同时刻各舰载机的飞行位置,图6给出了表4中舰载机着舰调度方案所对应的时序甘特图。其中,不同颜色的图例所对应的字母与图1中的字母含义相同,用以表示舰载机在返航航线中所处的位置。 图6 调度方案中各舰载机的飞行状态甘特图Fig.6 Gantt chart of flight status of each carrier aircraft in the scheduling scheme 作为比较,利用普通的GP算法、GA对上述着舰回收案例进行优化调度,所得的迭代收敛曲线如图7所示。 图7 不同算法的迭代收敛曲线Fig.7 Iterative convergence curves of different algorithms 从图7可以分析出,无论是算法的收敛速度还是算法的优化效果,本文所设计的MGP算法都是3种方法中最优的。这主要得益于MGP算法引入了强制优先着舰规则,使得油量不足的舰载机可以不受组合优先级规则的限制而实现提前着舰。引入强制优先着舰规则后,在相同的情况下,可以降低着舰方案中舰载机出现空中加油的可能性,避免了部分组合规则因出现空中加油而获得较大的评价指标函数,从而被过早淘汰的情况,变相地增加了种群的多样性,因此其优化效果相对于普通的GP算法有较为明显的改善。另一方面,在此案例中,机群的回收数量较多(30架),在利用GA进行方案优化时,其搜索空间的规模为30!,因而搜索效率较低,且极易陷入局部最优,从而影响了最终的优化效果。 图8中给出了利用GP算法、GA进行调度优化时所得到的着舰方案甘特图,两种算法的计算求解时间分别为12.6 s和23.2 s。可见在算法的求解速度方面,GP算法的求解耗时最短,MGP算法的求解时间较GP算法长3.8 s,但这一时间差距相较于着舰回收任务的总时长(55 min)而言,可忽略不计;GA的求解时间最长,其计算耗时约为GP算法的两倍。 图8 不同调度方案中舰载机的飞行状态甘特图Fig.8 Gantt chart of aircraft flight status in the different scheduling schemes 为了进一步验证本文所设计的MGA算法的有效性,此处选取GP算法、GA以及油少先着舰(less fuel first served, LFFS)启发式算法和优先级高先着舰(higher priority first served, HPFS)启发式算法作为对比。构建机群规模分别为15架、25架、35架、45架的回收案例,在每种机群规模下各进行30次仿真实验,将不同机群规模条件下的实验结果取平均值,获得的调度方案指标统计结果如表5所示,加粗字体的数值表示各组仿真结果中的最优值。 表5 不同机群规模条件下的算法优化结果统计结果Table 5 Algoribhm optimization statistic results under different aircraft fleet sizes 从表5可以看出,在4种机群规模条件下,本文所设计的MGP算法的调度结果均为最优。利用MGP算法和GP算法求解所得的着舰回收方案,其任务完成时间较另外3种算法而言更短。当机群数量较少时,GA的结果要优于纯启发式算法,但是随着机群规模的增加,GA的相对优化效果逐渐变差,且当舰载机机群规模增加到45架时,利用GA所获得的着舰方案中出现了空中加油的情况,且从适应度函数值来看,此时GA的优化效果差于LFFS算法。这是由于当机群规模增加时,GA算法的解空间将按照阶乘的方式急剧增大,其寻优性能相应变差。在全部的5种算法中,HPFS算法所得的着舰方案效果最差,且方案中出现空中加油的架次最多。HPFS算法和LFFS算法均属于启发式算法,其调度方案的合理性完全依赖于主观确定的启发式规则,且不具备迭代优化能力。但相对而言,LFFS算法可以保证着舰方案中的空中加油架次尽可能地少,从而使适应度函数中的惩罚项获得较小的值。除了LFFS算法,采用MGP算法和GP算法在4种不同机群规模的情况下所获得的着舰方案均不需要进行空中加油。 表5还给出了各种算法单次迭代的计算耗时,即算法的求解总耗时除以算法的迭代次数所得到的结果。从表5可以看出,HPFS算法和LFFS算法作为纯启发式算法,求解速度最快,单次迭代的计算耗时较另外3种算法小2个数量级,且由于HPFS算法和LFFS算法不需要迭代优化,因而其单次迭代的计算耗时即为算法求解的总耗时。在所有的算法当中,GA的单次迭代求解耗时最长,MGP算法的单次迭代求解耗时略长于GP算法,但MGP算法与GP算法的单次迭代求解耗时相差不超过15%。 本文所设计的MGP着舰排序方法可以给出经过优化后的着舰方案,但在实际情况中,舰载机着舰存在一定的失败概率。舰载机着舰失败后需要重新进行着舰,因此必须有相应的着舰失败应对策略。本文采用着舰失败的舰载机优先着舰的策略,即当出现逃逸或复飞的情况时,着舰失败的舰载机立即转入复飞航线,并在当前时刻已经经过马歇尔点的飞机全部完成着舰后再进行着舰,而未经过马歇尔点的舰载机利用其下层等待航线进行盘旋等待,待与二次着舰机的尾流间隔满足要求后再进行着舰。本文将最短复飞航线的飞行时间取为417 s。 在表4中的原有着舰方案的基础上,需考虑舰载机出现逃逸复飞时对着舰任务完成时间以及评价指标函数所产生的影响。此处在原方案中随机选择不同的舰载机,假设其出现了逃逸或复飞的情况,此时经过应急调整后的着舰方案所对应的任务完成时间以及评价指标函数如表6所示。由表6可见,与原着舰方案相比,当出现一架次舰载机着舰失败时,着舰任务的完成时间平均增加了139.3 s,指标评价函数平均增加了595.6 s,而当出现两架次舰载机着舰失败时,着舰任务的完成时间平均增加了273.0 s,指标评价函数平均增加了1 071.4 s。由此可见,提高舰载机的着舰成功率对于缩短回收任务完成时间以及增强回收任务效能而言有着重要意义。 表6 复飞逃逸对着舰排序方案的影响Table 6 Influence of wave off and escape on the landing sequencing scheme 本文首先对航母甲板环境以及舰载机的返航回收进场模式进行了分析,建立了基于加权等待时间的回收排序评价指标模型,并根据舰载机回收着舰问题中的各项约束,建立了考虑空中加油条件下的舰载机着舰回收排序调度问题模型。进一步,借助于超启发式算法思想,设计了一种基于MGP算法的舰载机机群回收排序调度方法,最后通过回收仿真算例验证了本文中模型和算法的有效性。本文的研究内容以及方法的优势主要体现在: (1) 在着舰回收调度模型中充分考虑了空中加油对着舰方案的影响,并给出了加油返航机的着舰回收方案,这使得调度模型对于返航舰载机的油量限制大大减小,提高了文中所建模型的适用范围。 (2) 通过GP算法进行组合调度规则优化,该方法与传统的遗传算法相比,最大的优势是其在机群规模增大的情况下可以保证解空间的搜索范围不变,因而具有较高的算法搜索效率。 (3) 在传统的GP算法中引入了强制优先着舰规则,尽可能地避免了着舰方案中出现空中加油的情况,同时也避免了部分组合规则因出现空中加油而获得较大的评价指标函数,从而被过早淘汰的情况,变相地增加了种群的多样性,这也使得MGP算法相较于GP算法而言具有更好的优化效果。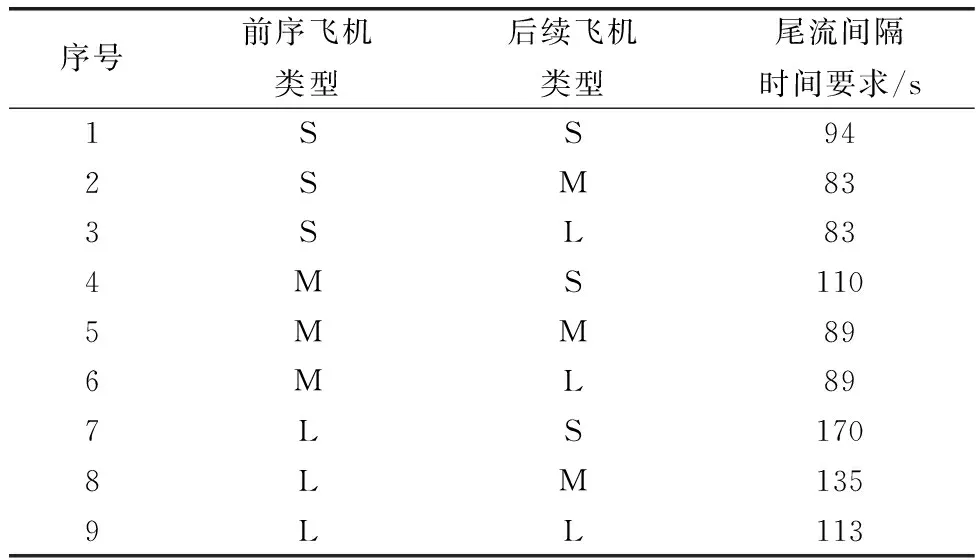
1.3 基于加权等待时间的回收调度评价指标
1.4 舰载机机群回收排序调度模型
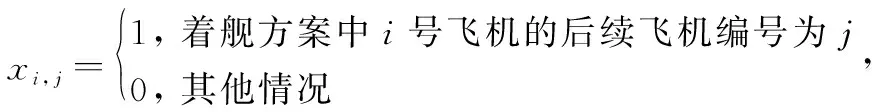
2 基于MGP的舰载机机群回收排序方法
2.1 调度优先规则的选取


2.2 编码设计与种群初始化


2.3 调度方案生成与适应度评价


2.4 种群的多样性操作
3 机群回收仿真分析与对比
3.1 机群回收着舰仿真条件设置

3.2 仿真结果分析与对比





3.3 逃逸复飞对着舰方案的影响分析

4 结 论

