基于复杂网络理论的发射平台抗毁伤网络拓扑性质研究

黄 通, 高钦和, 刘志浩, 王 冬, 马 栋, 高 蕾

(火箭军工程大学导弹工程学院, 陕西 西安 710025)

0 引 言

发射平台作为执行重要作战任务的特种武器装备,担负着导弹的储存、运输和发射的重要功能,通常部署在远离对峙前沿的隐蔽纵深地域。然而,近年来,随着各类先进侦察和探测技术的快速发展,加之发射平台原本的高分辨典型特征,使得发射平台在现代战争中被对方侦察发现的概率增大。同时,对方各种远程精确制导运载体携带的高性能先进战斗部,也给发射平台在战场环境中的生存能力带来了严峻的挑战。因此,评估发射平台在战场威胁环境中的抗毁伤能力,成为了提升发射平台战场生存能力的迫切需求[1-2]。

目前,在相关研究学者针对包括发射平台在内的武器装备抗毁伤能力评估的研究中,提出了多种评估和表征方法,如失效树法[3]、降阶态法[4]等。这些方法基本采用系统部件分解,从武器系统层面开始,再逐层向下分解到武器系统的子系统、部件、单元等,并用树形结构表示各部分的相互关系,实现目标内部逻辑结构的数学描述[5]。尽管这些方法能够满足评估问题的需求,但没有考虑到子系统和部件在系统中的布置方位对毁伤传导的影响,同时还存在对各子系统或各部件级相对重要程度的赋权问题[6-7],子系统的权重分配也因此成为了现阶段抗毁伤能力评估研究的关键和重点问题[8-10]。

现阶段的赋权方法大体上可分为主观赋权、客观赋权和主客观混合赋权。常见的主观赋权主要基于专家评分法[11-12],主客观赋权是在专家评分的基础上采用相关的数学算法进行混合赋权。文献[13]基于灰色聚类和相邻优属度熵值法对地空导弹武器系统的指标进行了主客观混合赋权;文献[14]基于层次分析法和灰色主成分分析法提出了一种适用于非线性多元时间序列分析的主客观分析方法;文献[15]基于反向传播(back propagation, BP)神经网络,通过专家评分数据集的训练对权重进行修正和调整。此外,还有灰关联[16]、贝叶斯网络[17]和模糊理论[18]等混合赋权方法,大多是采用专家评分的主观权值为基础数据,容易造成所赋权值的主观性较强、可信度下降等问题[19-21]。

复杂网络理论是一种从系统角度出发,通过研究系统本体结构与功能来探究系统内部复杂关系的方法[22]。因此,在传统方法对各个子系统之间的相互关联无法进行精确的问题描述时,采用复杂网络理论不仅可以精简模型,更能够有效地分析复杂系统的结构特征和功能运行机理[23],进而根据各子系统或部件在系统中的相对重要程度进行客观赋权。目前,复杂网络理论已经在交通[24]和电力系统[25]等领域中获得应用,在网络节点重要度[26-27]和网络抗毁性研究[28-29]中已经较为成熟。

基于上述内容,本文将复杂网络理论引入发射平台抗毁伤能力评估研究中,从毁伤流信息传导的角度,构建从毁伤源到发射平台总体功能的传导网络拓扑模型,研究分析该传导网络的拓扑性质。针对发射平台功能运行特性,采用互信息模型对关键部件的权重进行计算,提出节点连通度的发射平台抗毁伤能力表征方法,从复杂网络角度探究发射平台抗毁伤能力的防护途径。

1 抗毁伤网络建模

1.1 网络拓扑模型

发射平台在设计定型后即具有固定的结构特征和功能运行机制,由于毁伤过程在空间中的传导是由外向内的,因此不同于传统失效树的由系统到部件的建模思路,基于毁伤流信息由外向内的传导过程,建立由毁伤源到发射平台运行功能的网络拓扑模型。为了精简模型,做出以下假设。

(1) 将毁伤流信息传导过程中的部件或者高度集成的子系统、功能模块视为复杂网络的节点,将传导过程中的毁伤路径视为边。

(2) 由于毁伤流传导过程从物理上而言是有方向性的,且在整个过程中不存在相反方法的毁伤流,因此考虑单向边的形式,认为该网络中的边均为有向边。

(3) 不考虑毁伤源的毁伤类型、毁伤威力以及落点相对位置的影响,则同一层级的毁伤路径具有相同的流通概率。

基于上述假设,构建某重型机动冷发射的平台抗毁伤网络拓扑模型,如图1(a)所示,将其转化为复杂网络的节点和边进行表达,如图1(b)所示。

图1 发射平台抗毁伤网络拓扑模型Fig.1 Launch platform anti-damage network topology model

1.2 网络统计指标

复杂网络模型的研究基础是其基本的统计特征参量,诸如表示网络节点特征的节点度ki,节点平均度和度分布Pk,以及表示节点间关系特征的平均路径L和聚类系数γ等。在表征抗毁伤能力时,随着网络中节点和边定义的改变,以上特征参量也相应地发生改变,被赋予了抗毁伤特性的物理含义。

设该网络为G=(V,E),其中V={v1,v2,…,vn}表示中节点的集合,E={(vi,vj)|vi,vj∈V}表示中边的集合。记An×n=(aij)n×n为对应的邻接矩阵,有aij=1,否则aij=0。

(1) 聚类系数用来刻画发射平台抗毁伤网络的局域结构特点,研究抗毁伤网络的模块性和层次性:

(1)

式中:Ci=2Mi/[ki(ki-1)]为节点i的聚类系数,其中ki为个节点实际存在的边数,n为节点数量。

(2) 平均路径表征网络中节点之间的平均分离程度,可以用来刻画发射平台功能破坏的平均路径:

(2)

(3)

式中:U为单位指示函数,当i=j时,δij=1,否则δij=0。l为i,j两节点之间的最短路径长度。

(3) 度分布表征网络中节点度的概率分布,用来研究抗毁伤网络的基本结构特性:

(4)

(5)

式中:kmax为节点度的最大值。

(4) 节点介数表征经过某节点的最短路径数目和网络中最短路径数目的比值,用来研究毁伤流信息传导节点在抗毁伤网络中的影响力:

(6)

2 抗毁伤网络特征分析

本文对发射平台抗毁伤网络特性进行分析,构建了具有37个节点、109条有向边的抗毁伤网络模型,计算得到该网络拓扑结构的基本参数如表1所示。在该网络中,节点度的最大值为16,最小值为3,最大入度为15,最大出度为10。网络中各节点度值差距较大,说明发射平台的结构和功能布置分布不均匀。网络直径为5,从毁伤源到发射平台总功能的最短路径为3,平均最短路径为0.277。这说明发射平台抗毁伤的层次深度不足,毁伤源很容易到达核心功能,对发射平台的功能造成破坏。平均聚类系数为0.291,网络节点呈现出明显的局部集聚现象,反映了现实中发射平台的模块化程度。

表1 发射平台抗毁伤网络拓扑参数Tab.1 Launch platform anti-damage network topology parameters

2.1 节点度分布

发射平台抗毁伤能力受到各子系统和部件布置方位等因素影响,考虑到其网络节点度的有向性,网络节点度可以分为指向节点的入度和背向节点的出度,经计算得网络节点度分布如图2所示。

图2 抗毁伤网络节点度分布Fig.2 Node degree distribution of anti-damage network

由图2可知:① 发射平台抗毁伤网络节点度主要分布在两个等级。其中,度值为3和4的节点占比最多,分别达到33%和48%,表明抗毁伤网络中大部分节点存在3到4条连接边,这符合结构部件在空间布置中的邻接特点。其次,度值大于5的节点合计占比为19%,这表明抗毁伤网络中存在一定数量的通过频率较高的节点,这些节点是毁伤流信息传导的关键节点,需要有针对地增强防护;② 发射平台抗毁伤网络节点的入度和出度在大小和分布上差别较大。其中,入度最大值为15,出度最大值为10,出度、入度大于5的节点占比均为15%;入度值为1的节点占比最大,达到50%,出度值为1和2的节点占比均为53%。这表明,毁伤流在发射平台中的传导虽然具有一定的交叉汇集性,但主要以层级分散传导为主,这是由发射平台的高度集成化和模块化所决定的,这使得各子系统和部件之间的布置相对独立,但功能又需要汇聚集成;③ 发射平台抗毁伤网络度分布在节点度为4时出现峰值,当度值增大时,分布概率快速衰减,网络度分布呈现出近似Poisson的分布,因此发射平台抗毁伤网络不具备无标度网络特性,而属于指数网络。

2.2 聚类系数

按照抗毁伤网络节点度的有向性,聚类系数可以分为指向节点的入集和背向节点的出集,经计算得网络聚类系数如图3所示。

图3 抗毁伤网络聚类系数分布Fig.3 Cluster coefficient distribution of anti-damage network

由图3可知:① 发射平台抗毁伤网络的聚类系数除了少部分节点(节点25到节点31)为0,其他节点的聚类系数均在0.2上下波动,这表明发射平台的抗毁伤网络具有较高的局部聚集现象,且紧密程度较为均匀,节点间联系较为密切。当某一节点遭到破坏时,容易波及到周围的邻接节点,这也间接地反映出该抗毁伤网络的抗毁性较差;② 发射平台抗毁伤网络的入集聚类系数分布波动较大。其中,入集较大的节点反映的是部件布置密集处,如节点7的适配器与弹体和发射筒之间的聚类关系,节点22的车桥与制动器和轮胎之间的聚类关系。大部分入集较小的节点反映了发射平台的模块化,如节点14到节点21即为分别布置在设备舱内的子系统或部件装置。同时也可以看出,毁伤流在进入发射平台抗毁伤网络过程中需要经过重要节点,这些节点是增强发射平台抗毁伤能力的关键部件;③ 发射平台抗毁伤网络的出集聚类系数与入集聚类系数相比较大,反映了由于集成化程度较高导致毁伤流传导路径增多的问题,间接表明了发射平台抗毁伤能力较低。

2.3 平均路径

平均路径是反映发射平台抗毁伤网络分离程度的参量,该网络的平均路径较小,聚类系数较大,表明了该网络属于小世界网络。同时,毁伤源到发射平台总功能的最短路径值,将直接反映发射平台的抗毁伤能力。该网络直径为5,从毁伤源到发射平台总功能的最短路径为3,可见发射平台抗毁伤能力的脆弱性。计算网络中毁伤源和总功能之间的路径值如图4和图5所示。

图5 剩余节点到总功能的距离Fig.5 Distance between remaining nodes and total function

由图4可知,毁伤源到发射平台抗毁伤网络中节点的路径距离呈现出较强的层次性,且主要为2和3的路径距离,距离为1的节点有4个,占比为10.81%,即毁伤流在传导过程中必须要经过此4个节点,才能向内层扩散。

由图5可知,各节点到发射平台总功能的路径距离主要为2,也存在少量距离为1和3的节点,分别为3个,这主要是由于发射平台的总功能由三部分子功能组成,其中任意一个功能遭受破坏后,发射平台仍具有一定的作战能力。此外,在节点2和节点4处,与总功能的距离为2,与毁伤源的距离为1,是毁伤源与总功能连接的重要节点,需要进行重点防护。

2.4 介数分布

介数用于衡量节点在整个网络中的作用力和影响力,计算发射平台抗毁伤网络的节点介数分布如图6所示。

图6 节点介数分布Fig.6 Nodes mediator distribution

由图6可知:① 发射平台抗毁伤网络中的节点介数主要分布在3个等级。介数值大于5的节点有7个,占节点总数的18.92%。节点介数最大值为28.254,这一节点(节点2)代表发射筒,表明发射筒在发射平台抗毁伤网络中影响力最大;介数值大于1但小于5的节点有19个,占节点总数的51.35%,这些节点代表的部件和子系统主要集中在次外层;介数小于1的节点所代表的部件主要布置在内层,且模块化程度较高,因此在抗毁伤网络中的重要程度较低;② 在代表最外层布置的发射筒、驾驶室、设备舱和轮胎的节点2、节点3、节点4、节点5中,介数值分别为28.254、6、10.231、20.845。表明在抗毁伤网络中影响力排序依次为发射筒、轮胎、设备舱和驾驶室,这是由于发射筒和轮胎直接影响到发射功能和机动功能,而设备舱和驾驶室的损毁需要再经过其所包裹的部件才能影响到功能,同时设备舱包裹的部件数量较多,因此设备舱的影响力高于驾驶室;③ 在发射功能、机动功能和通信功能中,影响力最大的是机动功能,介数值为16.367,其次为发射功能,介数值为12.844,影响力最小的是通信功能。发射平台中大量的部件和子系统仍然服务于机动功能,其次才是发射功能,但两者之间的差距不大。

2.5 聚-度相关性

基于上述计算和分析,发现在发射平台的抗毁伤网络中存在着一定的层次特征和模块特征,聚-度相关性是网络层次模块性的重要标志之一,计算发射平台抗毁伤网络的聚-度相关性如图7所示。

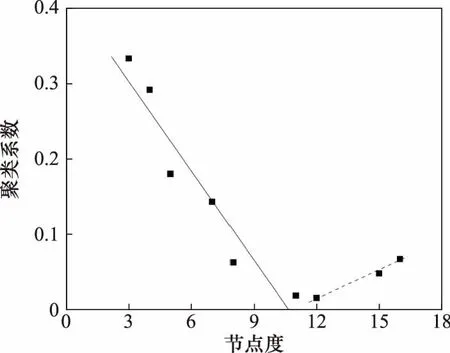
图7 聚-度相关性Fig.7 Poly-degree correlation

由图7可知,发射平台抗毁伤网络的聚-度相关性随着节点度值的不同,表现出两种特征。当节点度值小于11时,聚-度相关性符合幂律分布特征,抗毁伤网络呈现出层次网络特征,这是因为度值小于11的节点主要为发射平台的子系统或部件,这些子系统和部件本身就是按照层次和模块分解的;当节点度数大于11时,聚-度相关性不符合幂律分布特征,且与幂律分布的特征相反,这是由于度值大于11的节点主要为发射平台的子功能,这些子功能是将部件和子系统按照层次和模块集成的。因此,发射平台抗毁伤网络也属于层次网络。

3 抗毁伤网络的节点权重

综合第2节的计算和分析可知,发射平台抗毁伤网络中的各节点按照节点所对应的部件和子系统的布置方位存在3个层级,即外层部件(节点2到节点5),次外层部件(节点6到节点24),内层部件(节点25到节点33)。基于毁伤流信息由外向内的传导过程,布置在最外层的节点2到节点5最先遭受毁伤破坏,因此在抗毁伤能力综合评估问题中,对节点2到节点5所对应的发射筒、驾驶室、设备舱和轮胎权重的确定是综合评估的关键步骤。

尽管第2节中节点介数分布等参数的计算结果能够在一定程度上反映节点的重要程度,但没有全面地体现出抗毁伤网络中毁伤流的有向传导特征。因此,本文引入复杂网络理论中的互信息模型对抗毁伤网络中外层节点的权重进行客观计算。

对于有向网络,节点存在接收信息和输出信息的双重特征,在互信息模型[30]中,定义节点i的出边概率为

(7)

定义节点j的入边概率为

(8)

式中:kin和kout分别为节点的入度和出度。

则节点i到节点j的互信息I(i,j)为

(9)

定义节点i的信息量是节点i到所有i指向节点的互信息之和减去所有指向i的节点到节点i的互信息之和,即有:

(10)

式中:Vout(i)为节点所指向的节点集合;Vin(i)为指向节点的节点集合。

可以看出,节点的出度和入度越大,节点的互信息值越大,节点的信息流越大,节点就越重要。计算抗毁伤网络中外层节点的互信息值如表2所示。

表2 外层节点的互信息值Tab.2 Mutual information values of out layer nodes

由表2可知,外层节点的互信息值最大的是节点2发射筒,为19.442 3,然后依次是轮胎、驾驶室和设备舱,且发射筒和轮胎的互信息值相近。互信息值计算结果与节点介数相比,分布规律大体一致,但在驾驶室和设备舱的排序上相反,这是由于发射平台的设备舱包裹的部件和子系统较多,所以在介数计算中幅值较大,而驾驶室所包裹的部件和子系统虽然相对较少,但聚集性较高。因此,采用互信息模型计算网络中节点的重要程度所包含的特性更为全面。对外层节点的互信息值进行归一化处理后,即可将其作为各自的权重,用于抗毁伤能力的赋权评估。

4 基于抗毁伤网络的发射平台防护

复杂网络理论中的网络博弈研究方法可被应用到发射平台的防护优化中,即如何降低从毁伤源到发射平台功能的毁伤链路的连通性。本节首先从毁伤源到发射平台功能的连通性出发,采用两个节点的连通度对发射平台的抗毁伤能力进行表征。

设毁伤源节点到发射平台功能节点的连通路径为S,则定义两节点之间的连通度t为连通路径中同一路径长度ds上的节点数Ns与路径长度之比的总和。即

(11)

式中:Vf为连通路径中路径长度的集合。

由式(11)可以看出,两个节点的连通路径中的节点数越多,连通度越高,毁伤流信息就更容易到达发射平台的功能;路径长度越长,连通度越低,毁伤流信息就越难传导到发射平台的功能,符合毁伤流信息在发射平台中的传导过程。计算毁伤源到发射平台各功能处的连通度如图8所示。

图8 发射平台各功能连通度Fig.8 Functional connectivity of launch platform

由图8可知,除通信功能,毁伤源到发射平台各功能处的连通度均比较高,毁伤流信息可以通过多个节点在较多的路径上传导到发射平台的功能上,这表明发射平台的抗毁伤能力较差。

按照复杂网络理论中的博弈方法,对连通路径中的关键节点进行蓄意删除,即通过增强该节点所对应的部件防护能力,来阻断两个节点之间的连通路径。计算关键节点蓄意删除后的连通度,如图9所示。

图9 关键节点删除后的连通度Fig.9 Connectivity after key nodes deleting

由图9可知,对于发射功能,删除设备舱节点后的连通度降低幅度最大,其次是发射筒,这表明对设备舱和发射筒增加防护,能够有效提高发射平台发射功能的抗毁伤能力;对于机动功能,删除发射筒节点后的连通度降低幅度最大,其次是轮胎,这表明对发射筒和轮胎增加防护,能够有效提高发射平台机动功能的抗毁伤能力;对于通信功能,需要增强设备舱和驾驶室的防护能力。

5 结 论

本文将复杂网络理论引入发射平台抗毁伤能力评估研究,从毁伤流信息传导的角度,构建了从毁伤源到发射平台功能的传导网络拓扑模型,研究分析了该网络的拓扑性质和关键节点权重的计算方法,提出了节点连通度的发射平台抗毁伤能力表征方法,从复杂网络角度分析了发射平台抗毁伤能力的防护途径,得出以下结论:

(1) 发射平台抗毁伤网络具有指数网络、小世界网络和层次网络的典型特征,网络直径小,平均路径短,网络模块层次性强,局部聚集性大,综合反映了发射平台抗毁伤能力较差、容易被毁伤破坏的特点。基于复杂网络的评估方法能够综合考虑结构总体布置和功能传递,使得评估结果更加系统、全面。

(2) 互信息模型计算网络中节点的重要程度所包含的特性,比介数表征更为全面,采用互信息模型能够客观地计算出关键节点在抗毁伤网络中的重要程度。发射平台外层部件,即发射筒、驾驶室、设备舱和轮胎归一化后的赋权值分别为0.421 8、0.155 5、0.054 9、0.367 8。与现有的评估方法相比,减小了主观赋权的影响,提高了模型可信度。

(3) 复杂网络理论中的博弈方法可以应用于发射平台的抗毁伤能力防护优化中。采用节点连通度可以综合表征毁伤流信息在发射平台中传导的难易程度;增强发射筒的防护,可以提高发射功能和机动功能的抗毁伤能力;增强设备舱的防护,可以提高发射能力和通信能力。