数字金融对碳排放强度的空间效应及影响机制

吴毅斌

(兰州财经大学 统计学院, 兰州 730000)

中国二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和[1]。中共中央国务院发布的《关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》[2]明确提出,为了实现低碳发展,需要依靠金融机构积极发展绿色金融。随着人工智能、互联网、大数据为核心的数字化进程在经济、金融等领域的覆盖广度不断增加,数字金融对碳排放影响的研究也在不断 深入。

已有研究数字金融对碳排放影响的文献主要集中在以下3个方面:①数字金融对碳排放的影响研究。碳排放与人类经济发展息息相关,近年来,中国在生产效率快速提升的同时也加大了对各类能源资源的利用,大量的碳排放导致环境污染加重,严重威胁到人类的生存,全球碳减排大势所趋。数字金融主要通过大数据、互联网、云计算、区块链等新型技术与传统经济金融领域深度融合。通过将数字化技术与传统金融业务的融合,创造了数字普惠金融体系,可利用大数据精准搜寻目标客户群体,解决“长尾群体”的融资困境,从而减少了线下的碳排放。陈晓红等[3]的研究已证实数字化技术发展具有抑制碳排放的作用。贺茂斌和杨晓维[4]认为高新技术型企业往往具有融资难、收益低、周期长等特点,数字金融可为这类企业提供充足的资金支持,提升科技型企业的技术创新水平以减少碳排放;且数字金融依赖数字化平台提供金融服务,减少了线下交易来往产生的碳排放,从而降低了碳排放。②数字金融对碳排放的空间效应研究。赵瑞娟和李薇[5]研究发现,数字金融与碳排放之间存在空间效应,由于邻近地区之间各类生产要素流动性强,可能会导致碳排放的“虹吸效应”或者“扩散效应”产生,因此数字金融发展可能对碳排放强度产生空间溢出效应。③数字金融对碳排放的影响机制研究。邓荣荣和张翱祥[6]认为数字普惠金融对碳排放的作用机制一方面可直接影响碳排放效率,其次还可通过技术创新、经济增长、产业结构3种渠道抑制碳排放。

那么,数字金融与碳排放之间到底有什么联系呢?数字金融的发展是否会抑制碳排放强度呢?如果有抑制作用,数字金融对碳排放强度是怎样的影响机制?数字金融是否会促进或者抑制邻近地区的碳排放强度呢?通过文献梳理发现,目前研究主要集中在金融发展对碳减排效率的实证研究,鲜有研究涉及数字金融对碳排放强度的影响,且尚未从多角度研究数字金融影响碳排放强度的传导机制,数字金融与碳排放强度之间的逻辑关系需要进一步厘清与完善。因此,基于以上分析,做进一步的拓展研究。利用双向固定效应模型、中介效应模型和空间杜宾模型实证检验了数字金融发展对碳排放强度的作用机制及空间效应。基于此提出关于抑制碳排放强度的相关政策建议。从数字金融的角度拓展了金融发展与碳排放强度的关系,为更好地发挥数字金融的碳减排效应提供稳健的实证依据和决策参考,以期促进中国碳减排效率,助力中国“双碳”目标的实现。

1 理论机制与研究假设

1.1 数字金融发展对碳排放强度的直接影响

数字金融发展对碳排放强度的影响包括以下几个方面:①金融机构可以借助数字化平台对精准掌握企业信息,提高金融资源配置效率,淘汰高污染、高耗能的企业[7];②碳排放权交易是国家通过市场规制影响碳排放、应对全球气候变暖的重要举措,碳排放权交易市场借助数字金融可以使碳金融产品更加大众化和普惠化,对企业碳排放行为通过市场交易的方法在惩罚和补偿之间进行平衡最终有利于减少企业碳排放的负外部性,实现碳减排工作;③利用数字金融平台可对企业信息全方位掌握,可为政府提供精准且全面的环保信息,实现精准且科学的决策,可根据碳排放对企业进行“奖优惩劣”,促进各地区碳减排。康曼和杜运伟[8]认为本地区的数字金融的提高,通过线上平台进行各种金融服务,加快了金融市场的交易进度,使交易市场更加快捷,而且提高了研发效率与技术创新,但这一过程也产生了“虹吸效应”,使邻近省份的资金与技术流向该地区,金融资源产生不合理配置,减缓了邻近地区的数字化进程,影响了邻近地区经济的发展,不利于生产设施升级改造,从而抑制了邻近省份的碳排放效率。因此提出以下假设。

H1:数字金融发展抑制了碳排放强度且具有正向的空间溢出效应。

1.2 数字金融发展对碳排放强度的影响机制

数字金融通过对金融资源的收集与合理配置促进经济增长。金融机构能够利用大数据、云计算等技术收拢金融资源,筛选具有发展潜力的企业提供充足的信贷支持,数字金融普惠性的特点,可使“长尾群体”更易得到金融服务,解决“长尾群体”融资难题,增加企业生产绩效。现阶段的研究成果认为数字金融会通过促进经济质量增长抑制碳排放[9]。刘玉珂和金声甜[10]认为数字金融的发展在增加自身的产值的同时也增加了服务业产值,且数字金融发展更易引导生产要素转向低能耗、高效率的企业。由于第三产业能耗低、排放少,产业结构的升级将有利于抑制碳排放强度;其次,数字金融促进了金融资源的合理配置,有效解决金融机构和企业间信息不对称问题,提高了金融资源配置效率,产业结构的合理化将使得能源等各类资源的利用效率提高[11],推进经济发展以绿色为导向,加快碳减排效率。综上,数字金融将会通过促进经济发展质量和产业结构升级影响碳排放强度,因此提出以下假设。

H2:数字金融通过促进经济发展质量和产业结构升级2种中介渠道抑制碳排放强度。

2 研究设计与变量选取

2.1 模型设定

2.1.1 基准回归模型

通过上文文献可得数字金融发展会对碳排放强度产生抑制作用,为实证检验数字金融发展对碳排放强度是否为抑制作用且显著,构建如下的理论模型:

ln Ceiit=β0+β1Difit+∑β2Xit+μi+λt+εit

(1)

式中:ln Ceiit为省份i在t年份的碳排放强度;Difit为数字金融发展指数;Xit为一系列影响碳排放强度的控制变量;β0为常数项;β1、β2为回归系数;μi为地区固定效应;λt为时间固定效应;εit为随机干扰项。

2.1.2 中介效应模型

式(1)重点关注的是数字金融发展对碳排放强度的直接效应,通过上文文献可知,数字金融发展对碳排放强度的影响主要是通过经济发展质量和产业结构升级,那么为了探讨它们之间具体的影响机制,参考温忠麟和叶宝娟[12]的研究,构建如下模型,对该影响机制进行实证检验。

Mit=α0+α1Difit+∑α2Xit+μi+λt+εit

(2)

ln Ceiit=η0+η1Difit+η2Mit+
∑η3Xit+μi+λt+εit

(3)

式中:M为中介变量,代表经济发展质量(Pgdp)、产业结构(Is);α1为数字金融对中介变量的回归系数;α2、η3为控制变量的回归系数;α0、η0为常数项,η1为数字金融对碳排放强度的回归系数;η2为中介变量对碳排放强度的回归系数。

2.1.3 空间面板模型

由于各地区之间数字金融与碳排放相互之间在空间上可能会产生影响,为研究两者之间是否具有空间效应,计划采用空间杜宾模型验证数字金融和碳排放强度之间的空间溢出效应,构建模型如下:

ln Ceiit=β0+ρ1Wijln Ceiit+β1Difit+ρ2WijDifit+
β3Xit+ρ3WijXit+μi+λt+εit

(4)

式中:Wij为空间权重矩阵;ρ1为空间自回归系数;ρ2为数字金融空间滞后的回归系数;ρ3为控制变量空间滞后的回归系数。空间权重矩阵采用反距离平方矩阵,其余变量含义与前文相同。

2.2 变量选取

2.2.1 被解释变量

被解释变量为碳排放强度, 采用各地区的碳排放总量与地区生产总值的比值取对数来表示碳排放强度。碳排放强度值越小,越能表明中国低碳发展模式越完善。2006年,联合国政府间气候变化专门委员会在《国家温室气体清单指南》中提出温室气体的增加除了自然界自身产生的之外,主要来源于人类对化石燃料的燃烧,并提出了根据燃料燃烧数量和燃烧因子测算计算碳排放量。因此,借鉴任志娟[13]对碳排放量的测度方法,采用煤炭、焦炭、汽油、原油、柴油、煤油、燃料油、天然气等8种能源的消耗量,计算各地区能源消费的碳排放总量。具体的碳排放总量测算方法为

CO2it=∑Eijtηj

(5)

式中:CO2it为i省第t年的碳排放总量;Eijt为i省第t年第j种能源消费量;ηj为第j种能源的二氧化碳排放系数。

2.2.2 解释变量

本文的核心解释变量为数字金融。现有文献大多采用郭峰等[14]编制的数字金融普惠指数作为数字金融发展程度的代理变量,数字普惠金融指数包含数字化程度、覆盖广度和使用深度3个维度。

2.2.3 中介变量

中介变量包括:①经济发展质量(Pgdp)。采用人均地区生产总值取对数表示。② 产业结构(Is)。借鉴王书华等[15]的做法,采用第三产业增加值与第二产业增加值的比重作为指标衡量产业结构合理化程度。

2.2.4 控制变量

参考以往的研究,控制了以下可能影响碳排放强度的变量:① 政府管制(Gov)。政府干预虽然能够对环境污染进行管制,但政府的过度干预不利于碳排放强度的降低[16]。采用地区政府财政支出总额与当地生产总值比重表示。②人口密度(Pop)。代表地区居民集聚程度,用平方千米的人口数表示。③ 科技支出(Tec)。科技水平越高,越能够促进投入要素的利用和创新成果的转化,从而减少碳排放[17],采用政府科学技术支出与财政支出比值衡量。④城镇化水平(Urb)。用各地区城镇人口占该地区年末常住人口数比重来衡量。⑤绿化水平(Gre)。衡量地区绿化环境建设,绿化水平高说明环境规制高,采用建成区绿化面积覆盖率表示[8]。⑥教育水平(Edu)。借鉴张元庆等[18]的做法,用高等教育人数衡量当地教育水平,具体以人口抽样调查数据中的大专及以上人口数占6岁以上总人口的比例来衡量。

2.3 数据来源

研究样本基于2011—2020年中国30 个省(自治区、直辖市)(因数据缺失,未包含西藏地区和港澳台地区)的面板数据。数据来源于国家统计局官方网站和各地统计年鉴。样本量为300个。变量描述性统计见表1。由标准差可得,数字金融指数之间存在着巨大的差距,表明各地区数字金融发展程度差异较大,区域之间发展不均衡。

表1 变量描述性统计

3 实证结果与分析

3.1 基准回归

根据Hausman检验结果,P为0.008 5,表明实证检验采用固定效应模型优于随机效应模型。故应用双向固定效应模型进行后续实证检验。结果见表2(1)列、(2)列,数字金融的回归系数为负且在1%的水平上显著,即数字金融每提高1个单位,碳排放强度便会相应地降低0.008个单位,初步证明了数字金融能够显著抑制碳排放强度。

表2 基准回归结果

3.2 内生性检验与处理

由于上述检验可能会存在遗漏变量从而导致内生性问题,且被解释变量与解释变量可能存在互为因果的问题,碳排放强度的高低可能会对数字金融的发展产生影响。该部分采用动态面板广义矩估计模型及工具变量法估计数字金融对碳排放强度的影响,从而解决内生性问题。

3.2.1 系统GMM(广义矩估计)

为了避免内生性问题对研究带来的干扰,构建动态面板模型;采用碳排放强度的滞后一期的作为解释变量,运用系统GMM(系统广义矩估计,System-GMM)模型进行回归估计,回归结果见表2第(2)列。表中AR(1)值显著, 但AR(2)值不显著,证明随机干扰项存在一阶自相关,但随机干扰项不存在二阶自相关,说明随机干扰项不存在序列自相关。Hansen检验的P大于0.1,说明不存在过度识别的问题,说明所有工具变量均有效,不存在过度识别问题。检验结果表明系统GMM模型回归结果是合理有效的,其回归系数方向和双向固定效应一致,证明数字金融对碳排放强度依然具有抑制作用,这与双向固定效应模型得出的实证结果一致,实证结果支持基准回归的结论。

3.2.2 工具变量法

采用工具变量法进一步解决内生性问题。因为数字金融指数滞后一期与当期数字金融发展高度相关,且与当期碳排放强度无关,所以将数字金融指数滞后一期作为数字金融发展的工具变量来进行二阶段最小二乘(2SLS)回归;将工具变量引入后,第一阶段结果见表2第(3)列。L. Dif 的系数在1%的水平上显著,说明当期与滞后一期的数字金融有着很强的相关性,且F大于10表明数字金融滞后一期不是弱工具变量;同时,工具变量的个数等于内生变量个数,即恰好识别,无须进行过度识别检验,说明该工具变量是有效的。表2第(4)列显示,回归系数显著为负且通过了1%的显著性检验,说明工具变量法的估计结果支持提出的假设。

3.3 中介效应检验

理论分析表明数字金融发展通过促进经济发展质量和产业结构升级抑制碳排放强度。利用逐步回归法对两种中介变量进行检验。表3第(1)、(3)列显示,数字金融的系数均为0.002且显著,这表明数字金融的发展有利于促进经济发展质量和产业结构升级;同时纳入两个变量之后,表3第(2)、(4)列显示,经济发展质量、产业结构的回归系数均为负且在1%的水平上显著。即验证了数字金融通过促进经济发展和产业结构升级对碳排放强度产生抑制作用的假设。

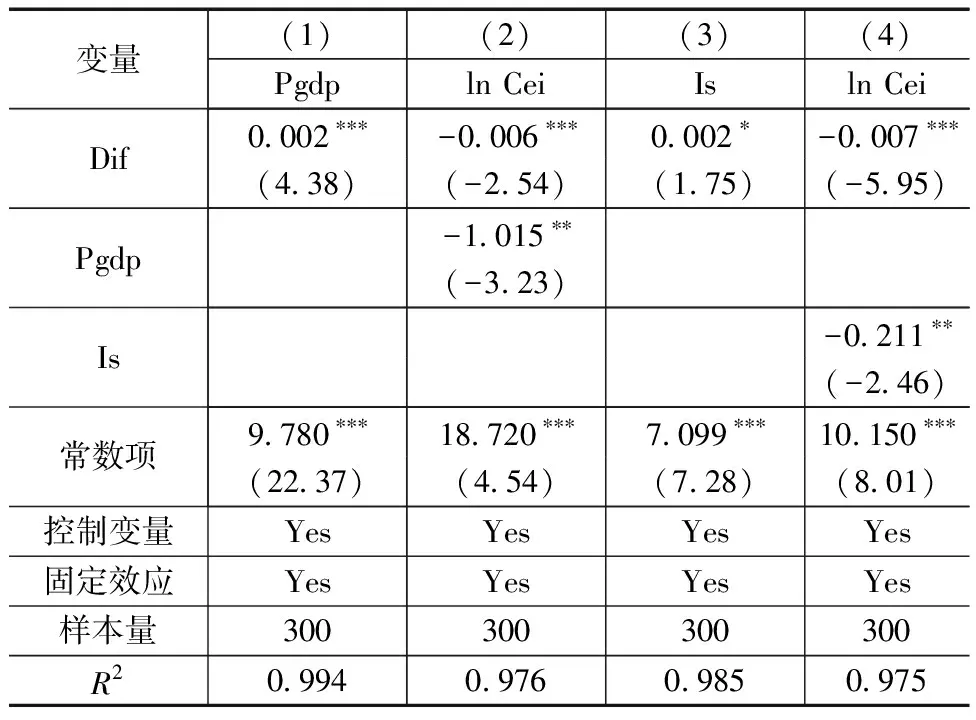
表3 数字金融对碳排放强度的影响机制估计结果

3.4 稳健性检验

采用数字金融指数的3个子维度数字化程度(Dig)、使用深度(Dep)替换核心解释变量数字金融指数进行回归分析,结果见表4第(1)、(2)列。数字化程度和使用深度的回归系数均为负且在1%的水平上显著,说明数字金融的数字化程度、使用深度、覆盖广度可以抑制碳排放强度,证明了基准回归的稳健性;人均碳排放量(Pce)也可反映某地区的碳排放强度,采用人均碳排放量表示碳排放强度,从而检验替换被解释变量后的结论是否仍旧成立,结果见表4第(3)列:数字金融的回归系数为负且在1%的水平上显著,说明数字金融发展可以抑制人均碳排放量,与上文实证结论一致,间接验证了结论的稳健性;为了消除数据极端值对实证检验结果造成影响,对所有变量进行了1%水平的缩尾处理。表4的第(4)列为对变量进行缩尾处理之后的回归结果,数字金融的回归系数依然为负且在1%的水平上显著,进一步验证了数字金融对碳排放强度的显著抑制作用,加强了对上述论证的解释。

表4 稳健性检验结果

4 空间溢出效应分析

4.1 空间自相关检验

空间相关性是指变量在空间中存在互相影响,通常采用莫兰指数检验空间相关性,选择反距离平方空间权重矩阵计算2011—2020年碳排放强度的莫兰指数,结果见表5。莫兰指数越趋近于1表明空间相关性越强,正负号则代表正负相关性。表5中2011—2020年莫兰指数均为正且在1%的显著性水平下通过检验,表明中国的碳排放强度在空间上呈现出正向空间相关性。可以在后续采用空间面板模型来分析数字金融对碳排放的空间效应。

表5 2011—2020年空间自相关检验结果

4.2 空间计量模型的适用性检验

该部分实证检验了数字金融对碳排放强度的影响是否适合采用空间计量模型来研究,结果见表6,根据检验可得, LM检验和稳健性LM检验均在5%的水平上显著,因此可以认为碳排放存在空间关系,本研究应采用空间杜宾模型。然后判断空间杜宾模型是否会退化为空间误差模型或空间滞后模型。结果显示,LR检验和Wald检验均在1%的水平上显著,表明本研究应使用空间杜宾模型。因此,选取双向固定效应的空间杜宾模型进行空间计量分析。

表6 空间模型检验结果

4.3 空间效应实证

根据上述检验结果,借助双向固定效应的空间杜宾模型(spatial Dubin model, SDM)估计数字金融对碳排放强度的空间效应。根据表7得到数字金融对碳排放强度的空间溢出效应结果:空间自回归系数rho为正且在1%的水平上显著,进一步证实了各地区碳排放强度具有空间集聚效应。Main为本地区的数字金融对本地区碳排放强度的影响,Wx表示本地区数字金融对邻近地区的碳排放强度的影响。表7(1)列、(2)列显示:Main的系数为负且在1%的水平上显著,说明本省份内的数字金融发展对本省份的碳排放强度具有显著的抑制作用,Wx系数为正且在1%的水平上显著,表明数字金融在空间上具有显著的正向溢出效果,即本省份的数字金融的发展会使邻近省份碳排放强度上升,即数字金融发展抑制本省份碳排放强度的同时会增强邻近省份的碳排放强度,假设1得到验证。

表7 数字金融对碳排放强度的空间溢出效应

由于空间杜宾模型解释变量相关项Wx的系数没有反映数字金融的全部作用效应,为了更直观地分析数字金融对碳排放强度的影响,将空间溢出效应分解为总效应、直接效应和间接效应,结果见表7(3)列、(4)、(5)列:直接效应和总效应的系数为负且在1%的水平上显著,表明本地区的数字金融对本地区的碳排放强度起到抑制作用,间接效应的回归结果为正且在1%的水平上显著,证明数字金融在空间上存在正向溢出效应,即本地区数字金融的发展会在空间上增强对邻近地区的碳排放强度,即验证了假设1。

5 结论与建议

5.1 结论

选取2011—2020年省级面板数据进行回归,以经济发展质量和产业结构升级为中介变量,运用双向固定效应模型、中介效应模型和空间杜宾模型深入探讨数字金融对碳排放强度的作用机制及空间效应,得出以下结论:

1)数字金融发展对碳排放强度具有显著的抑制作用,推动数字金融的发展能够使中国加速完成“双碳”目标;通过系统GMM和工具变量法做内生性处理后,该结论仍旧成立,且通过替换解释变量、被解释变量、缩尾处理等稳健性检验后,均证实了该结论。数字金融具备环境友好型特征,传统金融服务与数字化技术的融合能够通过减少线下交易及现金使用而促进碳减排,引导金融资源流向节能环保型企业,从而减少碳排放。

2)在作用机制方面,数字金融有助于提升地区的经济发展质量和产业结构升级,从而抑制了地区碳排放强度;数字金融有助于提高金融资源的配置效率,加快地区经济增长速度,即能为企业研发创新提供资金支持,也能通过引导金融资源流向节能环保型企业促进产业结构优化升级。

3)数字金融对碳排放强度具有正向空间溢出效应。数字金融在对本地区碳排放强度抑制的过程中反而提高了邻近地区的碳排放强度,说明存在负外部性;由于数字金融发展使邻近地区的技术资源流失,出现“虹吸效应”,导致邻近地区的碳排放强度增高。

5.2 建议

1)健全数字金融服务体系,提升数字金融对碳减排的贡献能力。由于数字金融显著的抑制了碳排放强度,应继续深化数字金融发展,运用数字化技术,搭建数字交易平台,直接减少线下的碳排放;重点推进数字金融以绿色为导向,发挥数字金融在实现中国“双碳”目标中的带动作用;此外,政府还应做好数字金融与企业技术创新的协调发展,如加强大数据、区块链等数字化设施的建设,促进碳减排效率,加快“双碳”目标的实现。

2)促进产业结构升级和经济发展质量的稳步增长。政府通过出台相关政策,加大对污染高、能耗高的企业的管制,促进各地传统产业向更高级产业转型;加强数字金融和产业的有效融合,带动经济发展质量的稳步增长,从而实现碳减排。

3)均衡数字金融空间发展程度。各地区应加强数字金融的覆盖广度、使用深度;加强各区域之间在低碳技术和产业优化等方面的合作,提升能源利用效率,减少二氧化碳排放;并注重与各区域发展的一致性,促进各地区间的数字金融协调发展,降低数字金融发展导致的空间负外部性,从而减少“虹吸效应”对邻近区域产业结构和碳排放的影响程度。