具有相依性元件的串联系统的冗余元件分配问题
李晓琴, 游银萍
(华侨大学 数学科学学院, 福建 泉州 362021)
在工业工程中,冗余分配是提高系统可靠性的常见做法.工程师通常采用冷储备和热储备这两种分配方式.热储备是指将冗余元件并联在工作元件上一同运行;冷储备是指将冗余元件置于备用阶段,只有当工作元件失效后才开始工作.目前,已有一些学者对冗余元件分配进行开创性讨论[1-10].其中,关于冗余分配的大部分研究都是在元件寿命相互独立的假设下进行的.然而,在实际问题中,工作元件都是在相同环境中运行,故考虑工作元件寿命具有相依性的相关研究更切合实际.在元件寿命相互独立的假设下, Misra等[5]和Romera等[11]分别研究了两个冗余元件下串联系统在随机占优序下的冗余冷分配问题和冗余热分配问题,证明了分配两个冗余元件中的一个冗余元件时,将寿命较长的冗余元件分配给寿命较短的工作元件可以延长系统寿命,分配两个冗余元件时,将寿命较长的冗余分配给寿命较短的工作元件的分策略较优.在工作元件寿命具有相依性的假设下,除了Belzunce等[12-13]和You等[14]建立了单个冗余元件下不同冗余分配策略的冗余串联系统寿命在随机占优序下的大小关系外,还未有关于工作元件寿命和冗余元件寿命相互独立且分别具有相依性的假设下串联系统在随机占优序下的冗余分配问题的研究.因此,本文在工作元件寿命和冗余元件寿命相互独立且分别具有相依性的假设下,研究分配两个冗余元件后的冗余系统寿命在随机占优序下的大小关系.
1 预备知识
在许多与概率相关的领域,如工程可靠性、金融精算、风险管理和统计等,随机序发挥着重要的作用,采用使用随机占优序来比较随机变量之间的大小关系.
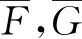
根据具有排列递增的相依概念,对于任意函数g:Rn→R,任意对(i,j),使1≤i 式中:τi,j(x)=(x1,…,xj,…,xi,…,xn)是向量x=(x1,…,xn)的一个置换. 定义2[15-16]向量X或者它的概率分布为 容易证明SAI⟹LWSAI. 对于连续型的随机变量,Li等[17]首次提出置换单调相依性的概念. 定义3称联合概率密度f(x)为 对于连续型的随机变量LTPD等价于LWSAI. 引理1~5在主要结论中起到关键作用. 引理2[15]设(X1,X2)是SAI的,当且仅当E[g2(X1,X2)]≥E[g1(X1,X2)],对于任意的x1≤x2,其中,g2,g1满足:1)g2(x1,x2)≥g1(x1,x2);2)g2(x1,x2)+g2(x2,x1)≥g1(x1,x2)+g1(x2,x1). 引理3[15-16]SAI和LWSAI性质的一些充要条件.1) 如果(X1,…,Xn)相互独立,那么X是SAI的,当且仅当X1≤lr…≤lrXn;2) 如果X1,…,Xn由生成元具有完全单调性的阿基米德copula耦合,那么X是LWSAI的,当且仅当X1≤rh…≤rhXn. 引理4[18]假设X的联合密度函数为f(x)=f(x1,…,xn),那么X是SAI的,当且仅当f(x)是排列递增的. 引理5[19]假设(X1,X2)是LWSAI的, 当且仅当E[g2(X1,X2)]≥E[g1(X1,X2)], 其中,g2,g1满足:1)g2(x1,x2)-g1(x1,x2)关于x1∈(-∞,x2]递减;2)g2(x1,x2)+g2(x2,x1)≥g1(x1,x2)+g1(x2,x1),对于任意x1≤x2. 建立引理6,7. 引理6对于任意的y1≥y2,令g1(x1,x2)=I(x2 证明:对于x1≤x2,容易得I(x2 对于y1≥y2和x1≤x2,有I(x1 引理7对于任意给定的y1≥y2,令g(x1,x2)=I(x1∨y2 证明:1) 固定x2∈[y2,y1]和x1≤x2,有I(y1 2) 固定x2≤y2≤y1和x1≤x2,有I(x1∨y2 3) 固定x2≥y1,x1≤x2,有I(x2 综上所述,对于任意的y1≥y2,可得Δg(x1,x2)关于x1∈(-∞,x2]递减. 研究具有相依性工作元件的串联系统分配两个热储备冗余元件中的一个热储备冗余元件和分配两个热储备冗余元件之后,冗余系统寿命在随机占优序下的大小关系. 假设分配两个热储备冗余元件中的一个热储备冗余元件后,两个系统寿命分别为 U1=(X1∨Y1)∧X2,U2=X1∧(X2∨Y2). 假设分配两个热储备冗余元件之后,两个系统寿命分别为 V1=(X1∨Y1)∧(X2∨Y2),V2=(X1∨Y2)∧(X2∨Y1). Romera等[11]考虑在工作元件寿命和冗余元件寿命相互独立的条件下,研究两种分配模型的冗余热分配问题,获得冗余系统寿命在随机占优序下的大小关系.其中,一种分配模型是分配两个热储备冗余元件中的一个热储备冗余元件,建立命题1. 由命题1可知:对于冗余元件寿命和工作元件寿命相互独立的冗余系统,分配两个热储备冗余元件中的一个热储备冗余元件时,将寿命长的热储备冗余元件分配给寿命较短的工作元件可延长系统的寿命.考虑到元件在相同环境下工作,故猜想可以将文献[11]的结论从元件寿命相互独立推广到工作元件寿命和冗余元件寿命相互独立且分别具有相依性的情形上. 由此可得在工作元件寿命和冗余元件寿命相互独立且分别具有相依性下的第1个结论(定理1). 定理1假设(X1,X2)是LWSAI的,(X1,X2)和(Y2,Y1)相互独立,且(Y2,Y1)是SAI的,则得到U1≥prU2. 证明:由文献[11]的命题1(a)可知,在几乎处处意义下U1>U2等价于 X1 故U1≥prU2等价于证明 P(X1 令g1(x1,x2)=I(x2 E[I(X1 对任意的y1≥y2,令 t1(y2,y1)=E[I(X2 由上式可得 t2(y2,y1)≥t1(y2,y1). (1) E[I(X1 即 t2(y2,y1)+t2(y1,y2)≥t1(y2,y1)+t1(y1,y2). 结合式(1)可知,t1,t2满足引理2的条件1),2),又因为(Y2,Y1)是SAI的,可推出E[t2(Y2,Y1)]≥E[t1(Y2,Y1)],即 E[I(X1 从而可得 P(X1 证毕. 定理1说明分配两个热储备冗余元件中的一个热储备冗余元件给具有LWSAI寿命的两个工作元件的串联系统时,将寿命较长的冗余元件分配给寿命较短的工作元件可以提高系统可靠性.引入例1,以说明定理1中寿命(Y2,Y1)的SAI条件是不可去的. 例1(Clayton copula) 对于任意x∈(0,1),贝塔分布B(a,b)的概率密度函数为xa-1(1-x)b-1/ Y的概率密度差值(Δg(y2,y1),0≤y2 图1 Y的概率密度差值(0≤y2 P(X1 ∭f(x1,x2)g2(y2)dy2dx1dx2= -0.002 349 67≤0, 该例子说明U1≥prU2是不成立的. 对于分配两个热储备冗余元件,Romera等[11]建立命题2. 命题2[11]假设X1,X2,Y1,Y2相互独立,如果满足X1≤hrX2和Y2≤hrY1,则有V1≥prV2. 由命题2可知:对于冗余元件寿命和工作元件寿命相互独立的冗余系统,分配两个热储备冗余元件时,将寿命较长的冗余分配给寿命较短的工作元件的分配策略较好.将上述结论从元件寿命相互独立推广到工作元件寿命和冗余元件寿命相互独立且分别具有相依性的情形上,得到第2个结论(定理2). 定理2设(X1,X2)是LWSAI的,(X1,X2),(Y2,Y1)相互独立且(Y2,Y1)是SAI的,则V1≥prV2. 证明:由文献[11]的命题2(a)可知,在几乎处处意义下V1>V2等价于 X1∨Y2 式中:X1∨Y2 因此,有 P(V1>V2)=P(X1∨Y2 类似可得 P(V1 由此可知,V1≥prV2等价于证明 P(X1∨Y2 E[I(X1∨y2 对任意的y1≥y2,令 t(y2,y1)=E[I(X1∨y2 由上式可知,对于y1≥y2时,有 t(y2,y1)≥t(y1,y2). E[I(X1∨Y2 从而可得 P(X1∨Y2 证毕. 由定理2可知,分配两个热储备冗余元件给工作元件寿命具有LWSAI寿命的串联系统时,将寿命较长的热储备冗余元件分配给寿命较短的工作元件的分配策略较优. 给工作元件寿命具有相依性的串联系统分配两个冷储备冗余元件中的一个冷储备冗余元件和分配两个冷储备冗余元件之后,冗余系统寿命在随机占优序下的大小关系. 假设分配两个冷储备冗余元件中的一个冷储备冗余元件后,两个系统寿命分别为 W1=(X1+Y1)∧X2,W2=X1∧(X2+Y2). 假设分配两个冷储备冗余元件后,两个系统寿命分别为 Z1=(X1+Y1)∧(X2+Y2),Z2=(X1+Y2)∧(X2+Y1). Misra等[5]考虑在工作元件寿命和冗余元件寿命相互独立的条件下,研究两种分配模型下的冗余冷分配问题,获得冗余系统寿命在随机占优序下的大小关系.其中,一种分配模型是分配两个冷储备冗余元件中的一个冷储备冗余元件,建立命题3. 命题3[5]假设X1,X2,Y1,Y2相互独立,如果X1或X2具有凸性的生存函数,那么当X1≤icvX2时,则有W1≥prW2. 由命题3可知:对于冗余元件和工作元件寿命相互独立的冗余系统,分配两个冷储备冗余元件中的一个冷储备冗余元件时,将寿命较长的冷储备冗余元件分配给寿命较短的工作元件可延长系统的寿命.将该结论从元件相互独立推广到工作元件寿命和冗余元件寿命相互独立且分别具有相依性的情形上,得到第3个结论(定理3). 定理3假设(X1,X2)是LWSAI的,(X1,X2)和(Y2,Y1)相互独立且(Y2,Y1)是LWSAI的,则有W1≥prW2. 证明:由文献[5]的定理2.4的证明可知,在几乎处处意义下W1>W2等价于 X1 由此可知:W1≥prW2等价于 P(X1 因此,要证明W1≥prW2等价于证明P(X1 对于任意的y1≥y2,令 t1(y2,y1)=E[I(X2 当x1≤x2时,易得I(x2 式中:P(X1>X2)是非负的,即 又因为-I(y2>0)关于y2∈(-∞,y1)递减,故可知t2(y2,y1)-t1(y2,y1)关于y2∈(-∞,y1)递减. E[I(X1 即 t2(y2,y1)+t2(y1,y2)≥t1(y2,y1)+t1(y1,y2). 对于任意的y1≥y2,综上可知,t1,t2满足引理5的条件1),2),又因为(Y2,Y1)是LWSAI的,可得E[t2(Y2,Y1)]≥E[t1(Y2,Y1)],即 E[I(X1 从而可得 P(X1 证毕. 定理3指出分配两个冷储备冗余元件中的一个冷储备冗余元件给具有LWSAI寿命的两个元件的串联系统时,将寿命较长的冗余元件分配给寿命较短的工作元件可延长系统寿命.为了更好说明定理3的结论,引入例2. 例2(Clayton copula) 假设X1,X2是失效率分别为2,1的指数分布函数,联合概率密度可表示为f(x1,x2),Y2,Y1服从标准指数分布,g2(y),g1(y)分别表示Y2,Y1的概率密度函数且(Y2,Y1)由Clayton copula耦合.X1,X2相互独立且X1≤lrX2,可知(X1,X2)是LWSAI的.又因为Y2≤rhY1,由引理3的条件2)可知(Y2,Y1)是LWSAI的.根据两个系统寿命概率分布函数可知它们的差值为 因此,W1≥prW2成立. 对于分配两个冷储备冗余元件,Misra等[5]建立以下结论(命题4). 命题4[5]假设X1,X2,Y1,Y2相互独立,如果X1或X2具有凸性的生存函数,那么当X1≤icvX2和Y2≤hrY1时,则有Z1≥prZ2. 由命题4可知:对于冗余元件寿命和工作元件寿命相互独立的冗余系统,分配两个冷储备冗余元件时,将寿命长的冗余元件分配给寿命较短的工作元件的分配策略较好.将该结论从元件寿命相互独立推广到工作元件寿命和冗余元件寿命相互独立且分别具有相依性的情形上,得到第4个结论(定理4). 定理4假设(X1,X2)是LWSAI的,(X1,X2)和(Y2,Y1)相互独立且(Y2,Y1)是LWSAI的,则有Z1≥prZ2. 证明:由文献[5]的定理3.1的证明可知,在几乎处处意义下Z1>Z2等价于 X2>X1,Y2 式中:X2>X1,Y2 因此,有 P(Z1>Z2)=P(X2>X1,Y2 类似可得 P(Z2>Z1)=P(X2 由此可知,Z1≥prZ2等价于 P(X2>X1,Y2 因此,要证明Z1≥prZ2等价于证明 P(X2>X1,Y2 对于任意的y1≥y2,令 t(y2,y1)=E[I(X2>X1)I(y2 Δt(y2,y1)=t(y2,y1)-t(y1,y2). 对任意的x1≤x2,y1≥y2,易得 I(x1>x2)I(y2 可得 根据引理1可知 E[I(X2>X1)I(Y2 从而可得 P(X2>X1,Y2 证毕. 定理4指出分配两个冷储备冗余元件给具有LWSAI寿命的两个工作元件的串联系统时,将寿命较长的冗余元件分配给寿命较短的工作元件的分配策略较好. 考虑在工作元件寿命和冗余元件寿命相互独立且分别具有相依性的条件下,分别研究串联系统下一个冗余元件和两个冗余元件的冷储备问题和热储备问题.利用随机序和相依性相关的定义和性质,建立不同冗余分配策略下串联系统在随机占优序下的冗余最优分配,研究表明,将寿命较长的冗余元件分配给寿命较短的工作元件的分配策略较好.注意到,串联系统是属于特殊的n中取k系统结构,因此,一个直接的想法是在工作元件寿命具有相依性下,考虑冗余分配之后n中取k系统的寿命之间的随机占优序关系,这将是今后工作的一个中心.
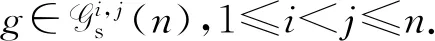
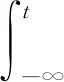
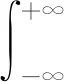
2 主要结论及其证明
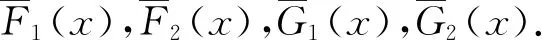
2.1 冗余元件热分配

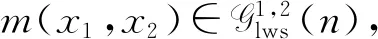

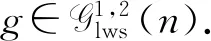

2.2 冗余元件冷分配
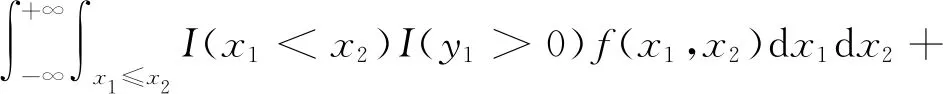
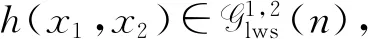
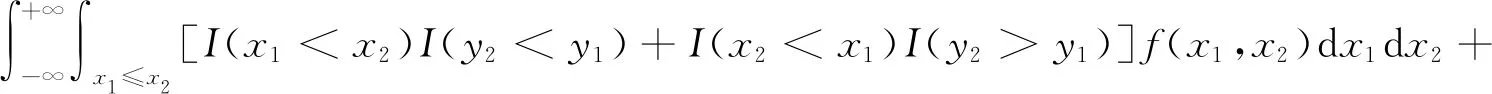
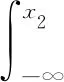

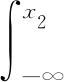
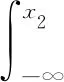
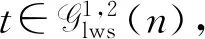
E[I(X23 结束语

