基于GRID-TIN方法的露天煤矿地表模型的仿真研究

李 洋,李 柯,李 渊

(山西大同大学,山西 大同 037003)

1 建模关键技术及方法

1.1 三维地质建模技术

三维地质建模(3D Geoscience Modeling,3DGM)的概念最早由加拿大学者Simon W. Houlding[1]于20世纪90年代提出。三维地质建模及可视化技术是煤矿智能化建设的基础,能够为真三维组态和四维地理信息系统提供地层支持,实现地形、煤岩层、断层、陷落柱、井巷系统等的真三维呈现[2-4]。由于强大的需求以及相关建模软件的发展,国外的三维地质建模技术已经实现飞速发展。国内的煤矿三维地质建模技术虽然起步较晚,但发展迅速,许多三维地质建模软件应运而生,并在地质学方面得到了广泛应用,在露天煤矿事故方面应用较少,主要是由于露天煤矿灾后的地质条件比较复杂,建模比较困难。

地形的三维显示技术是计算机图形学一个重要的研究内容,用于地形三维显示的数据按其数据结构类型可分为矢量型和栅格型两大类。其中,栅格型数据主要包括数字高程模型 DEM(Digital Elevation Model)和纹理图像数据[5]。数字高程模型DEM的数据结构一般有规则网格(Regular Grid)和不规则三角网(Triangulated Irregular Network)两种类型。Grid与TIN模型是一种表面模型,并非真正的三维模型,是2.5维的[6]。

1.1.1 Grid模型概述

Grid模型是由地形表面若干有规律的、连续的正方形组成的网格面,分辨率的不同影响着地图的显示效果。每个网格点对应一个高程值,在计算机中是二维数组,在数学中则可表示为矩阵,且每一个网格点都具有唯一行和列标识,若对Grid用数学方法进行平滑处理,则Grid在边界处连续可导。每一个网格都可以表示一个地理特征值。

它的优点是易获得,结构简单;缺点是当数据点分布不规律时,需要采用空间插值方法得到周围网格点的数据,不能精确表达具有断层的边界表面,当地形具有较多起伏时,无法细节地表达真实地形,当地形平坦时会产生数据冗余。

1.1.2 TIN模型概述

不规则三角网(TIN) 是一种DEM 表示方法,它适用于规则和不规则分布的数据,是将周围无重复的数据点进行组合,使其形成连续的不规则三角面网。三角形剖分可大致分为四种类型:普通三角形剖分、优化三角形剖分、最优化三角形剖分和Delaunay三角形剖分。采用构建Delaunay三角网[7]来实现地表模型的建立。它的优点主要在于:

1) 可以将等高线更好地融入到三角网中;

2) 可以跟随地形起伏变化改变采样数据点的位置和密度,在地形变化较为平坦的区域可以通过较大的三角面来表达地形,有效避免数据冗余;在地形变化较为剧烈的区域(如:边界、断面)可以通过较小的三角网来生成较为精确的表面模型。

1.2 建模方法的改进

根据露天煤矿灾后的实际地质情况(地形起伏较大、断面较多),采用Grid方法建立模型,虽然数据较易获得,但会使得模型表达较粗糙,采用Grid-TIN模型,即先用Grid函数生成规则网格点,之后通过构建Delaunay三角网来生成TIN模型,用于地形的表面模型构建,使得数据易获得的同时,对边界、断面等高低起伏的地形也可以进行较为准确的表达。

1.3 数据的插值

1.3.1 空间插值的目的

由于露天煤矿地形范围较大,以及事故后复杂的客观条件限制,现有的人员及设备无法获得足够多的数据,数据不够密集、采样率较低,用采集到的原始数据不仅无法准确完整地表达地形表面的实际情况,且误差较大,会导致绘制的三维地形曲面比较粗糙,建立的三维实体模型效果较差。需要采取恰当的空间插值方法获取足够多的采样点,以满足数据要求。

1.3.2 空间插值方法

常用的插值方法有克里金法、曲线的最小二乘拟合法、双线性内插法、趋势面法、三次样条插值法。MATLAB中常用的曲面插值函数有:Triscatteredinterp、interp2、griddata[8]。其中MATLAB中的griddata函数常应用于三维散点数据的插值,并且可以实现更高维度的插值,所以采用griddata函数对数据进行三维曲面的插值拟合处理。

2 三维地质模型的构建

2.1 地形测量数据处理

建立三维地质模型,首先要获取地质数据,地质数据是建立露天煤矿实体模型的基础,要正确处理数据,减少误差,保证露天煤矿地质模型的精度。首先选择露天煤矿事故后现场一段3 000 mm×3 250 mm的起伏地形,如图1所示,地形范围内最高为9.53 m,最低为0.2 m,煤层地形的整体变化趋势为由北向南、由中间向两侧变薄,间距增大。

图1 露天煤矿地形

通过仪器测量地形数据,并对数据进行预处理,删除异常高程点、重复点,进行交叉线检查、粗差检查,并进行数据冗余处理,避免在起伏较大的区域因为数据密集而造成的三维曲面不形象,之后获得该地形的一组二维矩阵DEM值,如表1所示。

表1 DEM值

2.2 现场实体模型的建立

2.2.1 初始三维曲面的建立

将获取的高程数据矩阵值保存到excel中,用MATLAB软件对其进行调用、处理,得到的三维曲面如图2所示。由于测量得到的地形数据较少,且数据未经过空间内插处理,导致高程点不够密集,曲面在表达地形的高低起伏变化方面不够细节,存在较大折痕,形成的实体也较为粗糙。

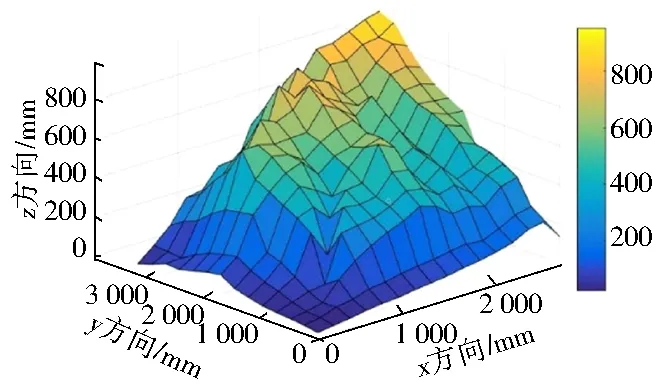
图2 三维曲面

2.2.2 插值运算后的三维曲面

首先采用meshgrid函数使新构成的网格点X的间隔为50 mm,Y的间隔为60 mm,之后用griddata函数进行插值运算,利用插值形成的Grid点生成Delaunay三角网,并计算三角剖分,用trisurf函数绘制由delaunay triangulation对象定义的三维曲面,如图3所示。经插值运算过后,地形过渡光滑、无较大折痕,可准确表达地形的起伏程度。

图3 插值后的三维曲面

2.2.3 地形实体

将经过插值运算后的数据保存到矩阵S中,其格式为S=[x(∶)y(∶)z(∶) ],将数据导入excel中进行处理。在AUTOCAD中,运用3DMESH命令生成曲面的三维网格图,之后将其保存成SolidWorks可识别的格式,在SolidWorks中打开。首先将各个曲面按照边界线各缝合成1个完整的曲面模型,之后采取封闭面固化成体的方法生成地形实体模型,即将每个曲面模型向水平面进行垂直投影,画出所有曲面的水平草图,再进行拉伸特征到曲面,最后生成煤矿现状实体模型。如图4所示,形成的实体较为光滑,无折痕,可以细节表达地形的起伏变化趋势。

图4 地形实体

2.3 模型的精度评价

三维地质模型精度评价是对地形精度的真实评价,影响三维地质模型精度的因素主要包括建模原始数据、插值方法的选择以及人工干预,采用熵权法对模型进行精度评价[9]。首先对影响因素进行识别,如表2所示。

表2 精度影响因素

之后根据影响因素表建立精度评议矩阵,并确定熵权,通过公式B=WR得到:B=(0.266 25,0.293 48,0.327 64,0.251 38)。根据计算结果可以看出,数值最大为0.327 64,最小为0.251 38,由此得出,影响因素对建模精度的影响较小,证明该地形建模结果误差较小,准确可靠。

3 结 语

1) 在三维建模技术的基础上,对建模方法进行改进,采用Grid-TIN方法构建露天煤矿实体模型,并进行插值处理以获得足够多的采样点,生成了较为真实的地形三维曲面。

2) 以SolidWorks为平台,采用封闭面固化成体方法,构建实体模型,能较好地反映地形的起伏。

3) 露天煤矿三维地质模型的建立,真实反应了地形的情况,达到了三维实体模型仿真效果,实现实体可视化,具有较好的工业应用价值。