双制式列车断路器合闸浪涌过电压研究

李雪飞 孙文斌 李明泽 马庆安 代 骏

双制式列车断路器合闸浪涌过电压研究

李雪飞1孙文斌1李明泽2马庆安3代 骏3

（1. 中车长春轨道客车股份有限公司，长春 130062；2. 四川轻化工大学自动化与信息工程学院，四川 宜宾 644000；3. 西南交通大学电气工程学院，成都 611730）

双制式列车在通过电分相或交直流转换段时，列车进行断路器操作产生操作过电压进而通过高压电缆的分布电容耦合至车体产生车体浪涌过电压，可能严重威胁车载弱电设备的安全运行。本文分析双制式列车合闸浪涌过电压的产生机理，为避免高阶微分方程的求解，将其分为两个振荡模式的乘积；搭建Simulink仿真模型，对双制式列车的合闸暂态过程进行仿真分析，并对列车浪涌过电压进行现场实测和频谱分析，理论分析与现场实测结果一致。研究表明，列车在经过电分相或交直流转换段时，最高可产生2 000V的车体浪涌过电压，该过电压在5ms内逐渐衰减至零，计算模型、仿真模型与实测数据误差率分别为17%和0.15%，因此，本文模型具有较高的可行性，可推进解决双制式列车浪涌冲击问题。

双制式列车；浪涌过电压；高压电缆；电容耦合

0 引言

目前，城轨铁路主要采用直流供电制式；干线铁路主要采用交流供电制式。双制式铁路同时存在交流和直流供电区段，需设立交直流转换段和交交分相区，因此双制式列车车载断路器动作次数远高于单一制式列车，进而频繁引起车体浪涌过电压、弓网匹配等问题。双制式列车和其他列车的不同主要在于双制式列车使用了电子式电压互感器以适用于交流、直流电压的检测。重庆江跳线的运行表明，车体浪涌过电压严重干扰了电子式电压互感器的正常运行，有必要展开研究。

目前，国内外学者已对干线铁路的车体升降弓浪涌过电压和操作过电压进行了广泛研究。CRH2型动车组升弓浪涌过电压幅值可达6.73kV并且在12ms内衰减[1]，该幅值与接触网等效参数密切相 关[2]。文献[3]从车体浪涌产生机理出发，分析升降弓车体浪涌过电压的传播规律及影响因素。文献[4]研究不同阻值的接地电阻器对车体浪涌的影响。文献[5]通过研究动车组车体浪涌对车载设备的影响，提出了几种抑制措施。文献[6]对锚段关节式电分相建立等效电路，并通过仿真分析得到了电源电压相位与中性线过电压的关系。文献[7]对接触网常见过电压进行分析。文献[8]针对列车升降弓车体浪涌过电压提出了两种抑制方法。

针对交直流双制式列车，文献[9]对双流制列车的车体环流及车体-轴端电位问题进行研究，并提出一种联合牵引供电计算方法。文献[10]使用CDEGS软件建立交直流双制式列车供电系统仿真模型，并提出一种适用于交直流双制式牵引供电系统的钢轨复合电位限值。文献[11]针对锚段关节式过分相，研究了列车过中性段的多种暂态过程。

目前，针对车体浪涌过电压，国内研究主要集中于列车升降弓操作引起的过电压，对于车载断路器合闸引起的车体浪涌研究较少，并且对于双流制列车通过中性段、分相区时产生的车体浪涌过电压研究甚少。本文结合两种过电压的数学计算模型，搭建双制式列车合闸浪涌仿真模型，并进行车体浪涌过电压实测验证，以实现对双制式列车合闸浪涌过电压的研究和分析。

1 双制式列车牵引供电系统分析

1.1 牵引供电结构分析

双制式列车在运行中存在单相工频27.5kV交流供电系统和1 500V直流供电系统的切换，双流制供电结构示意图如图1所示。其中，交、直流牵引网之间存在交直流转换段。

国内首条双制式线路“江跳线”的交直流转换段采用如图2所示的器件式分段绝缘方案。转换段使用4台分段式绝缘器将交直流转换段隔离为a、b、c三段。其中，b段永久接地。

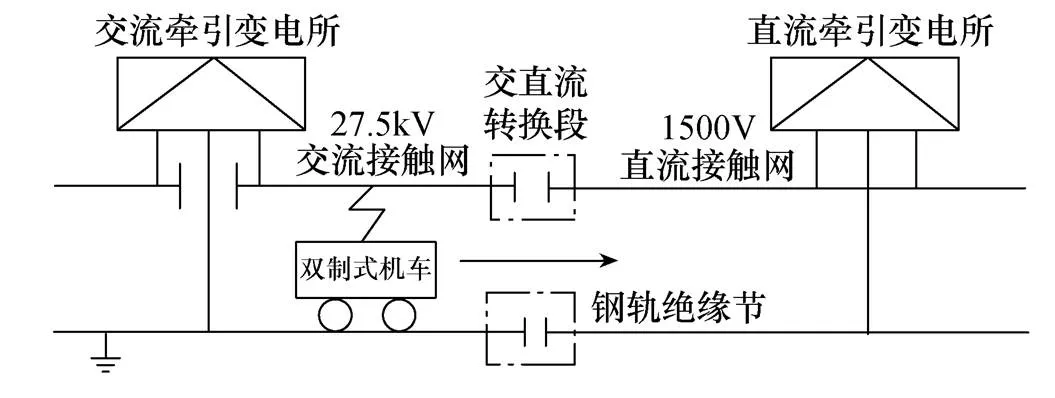
图1 双流制供电结构示意图

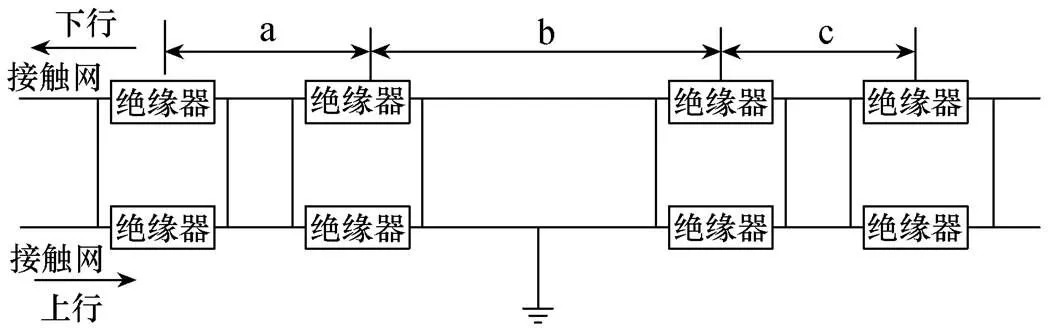
图2 器件式分段绝缘方案示意图

1.2 列车牵引主回路

江跳线双制式列车采用2动4拖编组方式。受电弓安装于2、5车车顶。1车～3车、4车～6车各为一个供电单元，两供电单元结构对称且电气部分相互独立。2车、3车之间用高压电缆相连。牵引主电路如图3所示。

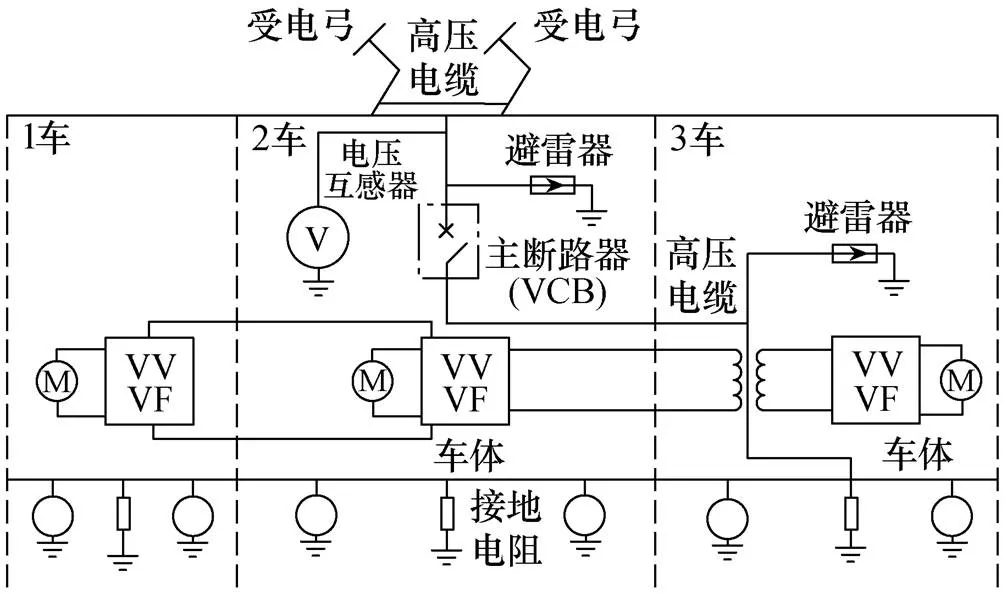
图3 牵引主电路

在交流运行模式下，供电单元由受电弓取电，经车载真空断路器（vacuum circuit breaker, VCB）、变压器和相应的交直交变流器给电动机供电。在直流运行模式下，供电单元由受电弓取电并直接馈送到交直交变流器的直流环节，逆变后给牵引电机供电。

当列车经过交直流转换段切换至直流运行模式时，由于VCB操作过电压较小，对车载设备无影响，因此本文不做讨论。本文仅研究切换至交流运行模式时的浪涌过电压。

2 车体合闸浪涌仿真分析

2.1 合闸浪涌过电压产生机理及计算分析

双制式列车经过交直流转换段进入交流区段后闭合VCB，将产生操作过电压[12]，而操作过电压为高频信号，将通过高压电缆的线芯耦合至屏蔽层，并由电缆屏蔽层接地点传至车体，造成车体浪涌过电压。

列车合闸时的车-网等效电路如图4所示。其中，S、S、S分别为牵引变电所的空载电压、内阻和电感；L、L、L分别为接触网等效电阻、电感和对地分布电容；开关K表示真空断路器（VCB）；m、m分别为车载变压器等效电感和对地电容；C、C和C分别为高压电缆分布电阻、电感和分布电容；T和T分别为列车的电感、电阻。

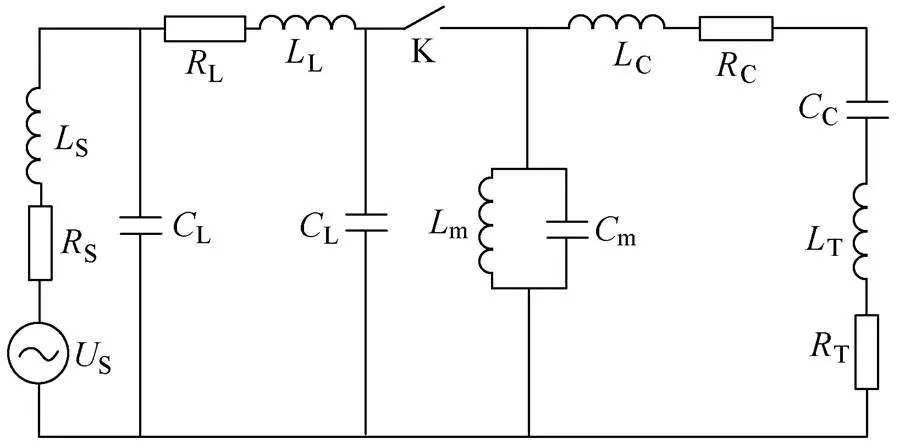
图4 列车合闸时的车-网等效电路

图4所示电路储能元件非常多，直接分析涉及高次微分方程的求解，非常复杂。为简化分析，这里把浪涌过电压简化为两个过程：由于牵引网对地电容L较小，可将其忽略，则m和系统电源并联。由于Sm且两者并联，故可忽略等效电感m。由于C+TS+L，Cm，则，故S+L和m组成一个低频振荡模式，C和C+T组成一个高频振荡模式，且前者是后者的调幅波。

1）振荡模式1

由S+L和m组成的低频振荡模式可由如图5所示VCB合闸等效电路说明。图5中，1=S+L，1=S+L。

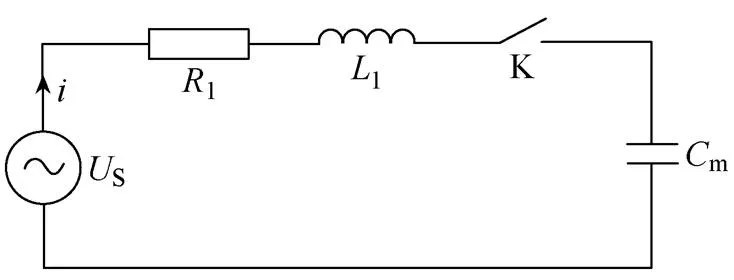
图5 VCB合闸等效电路

牵引变电所电源电压S=msin(+)。其中，为牵引所交流电源初始相位，m为牵引所电源电压幅值。

设VCB闭合瞬间，该回路电流和m的电压um存在的关系为

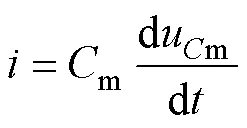
由基尔霍夫电压定律可得VCB闭合后的回路方程为

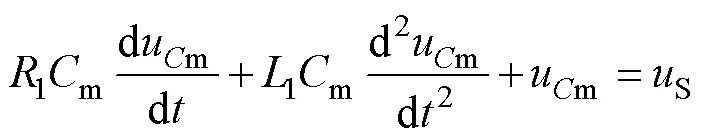
该方程对应的拉普拉斯方程为

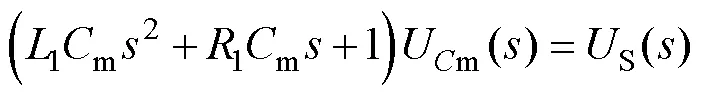
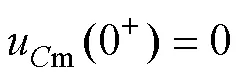
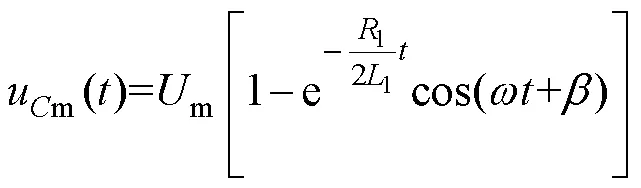
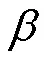
2）振荡模式2

由C+T和C组成的高频振荡模式可由如图6所示车体浪涌等效电路予以说明。由KVL可得该回路的微分方程为

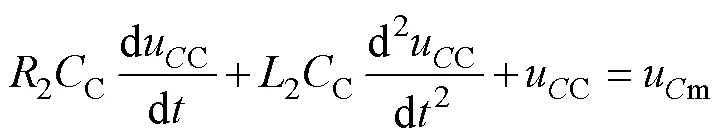
式中：2=C+T；2=C+T。

对式（5）进行拉普拉斯变换可得

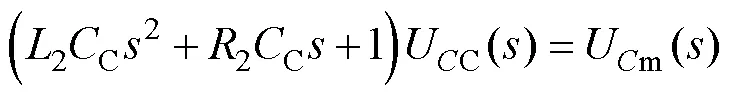
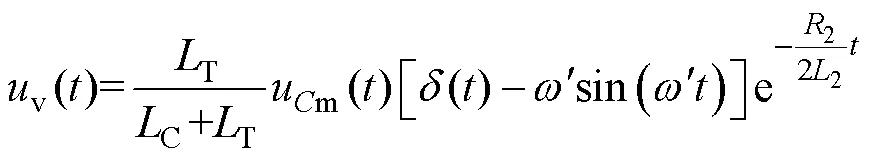
由式（7）可知，列车合闸浪涌过电压与合闸时的电源电压相位、高压电缆分布电感C及列车等效电感T有关。合闸时电源电压处于最值时产生的车体浪涌过电压最大；列车等效电感T越大，车体浪涌越大。

图4所示电路的车体浪涌仿真参数见表1。其中，v、v为单节车辆首、末端的电阻和电感；T、T为6辆车的总并联电阻、电感；h、h为单节车辆车体顶、底部的电阻和电感；g、g为列车等效接地电阻、电感。列车单个动力单元的高压电缆为20m，其单位长度分布电阻为0.2mW/m，单位长度分布电感为0.3mH/m，单位长度分布电容为0.5nF/m。

将表1数据代入式（7）可仿真得到车体浪涌过电压如图7所示，VCB合闸产生的浪涌过电压幅值为2 330V，并且在10ms内衰减至0V。

2.2 车体合闸浪涌仿真研究

为验证理论分析的正确性，本文建立车体合闸浪涌的仿真模型。

根据合闸浪涌过电压的产生机理及车-网等效电路，建立如图8所示的车体浪涌仿真模型，高压电缆使用RLC模型进行等效，不同供电单元高压电缆使用相互独立的断路器K1、K2进行表示，每节车厢设置两个并联的接地点及接地阻抗。

使用表1所示电气参数，分别设置VCB在0.505s、0.508s动作，可得到不同合闸相位对应的VCB合闸浪涌过电压波形如图9、图10所示。

图9中，VCB在0.505s闭合，接触网电压相位为90°，接触网电压幅值最大，产生了2 003.4V的车体浪涌过电压，并且在5ms内逐渐衰减至0V。图10中，VCB在0.508s闭合，接触网电压相位为144°，产生了幅值为1 195.1V的车体浪涌过电压，在5ms内逐渐衰减至0V。可见，列车浪涌过电压与VCB合闸时刻有关。

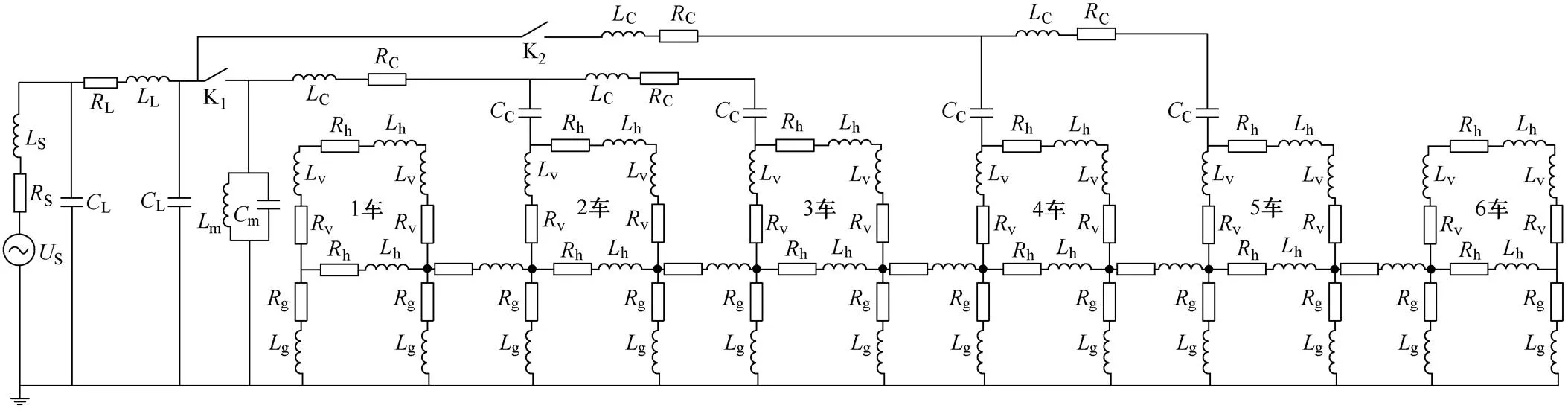
图8 浪涌仿真模型

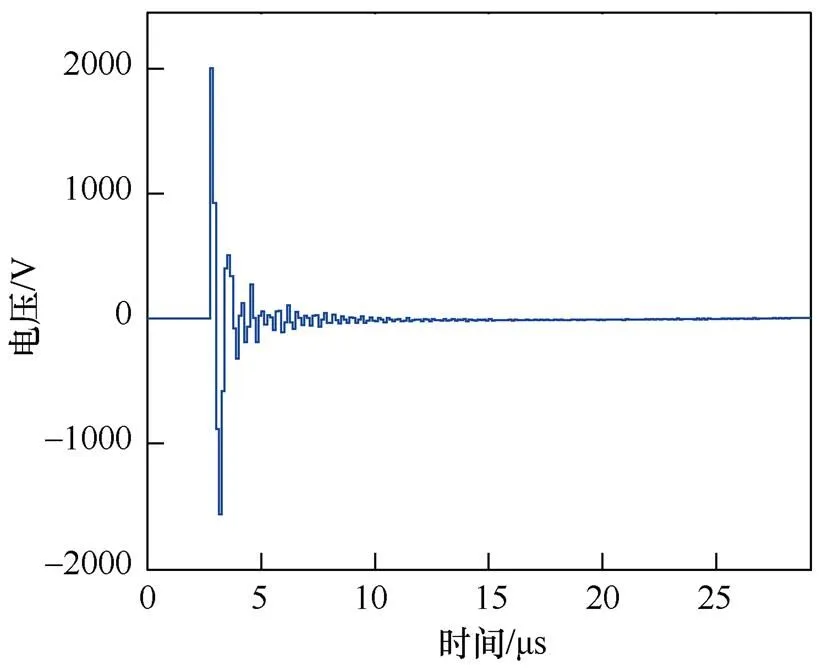
图9 合闸相位为90°时的VCB合闸浪涌过电压波形

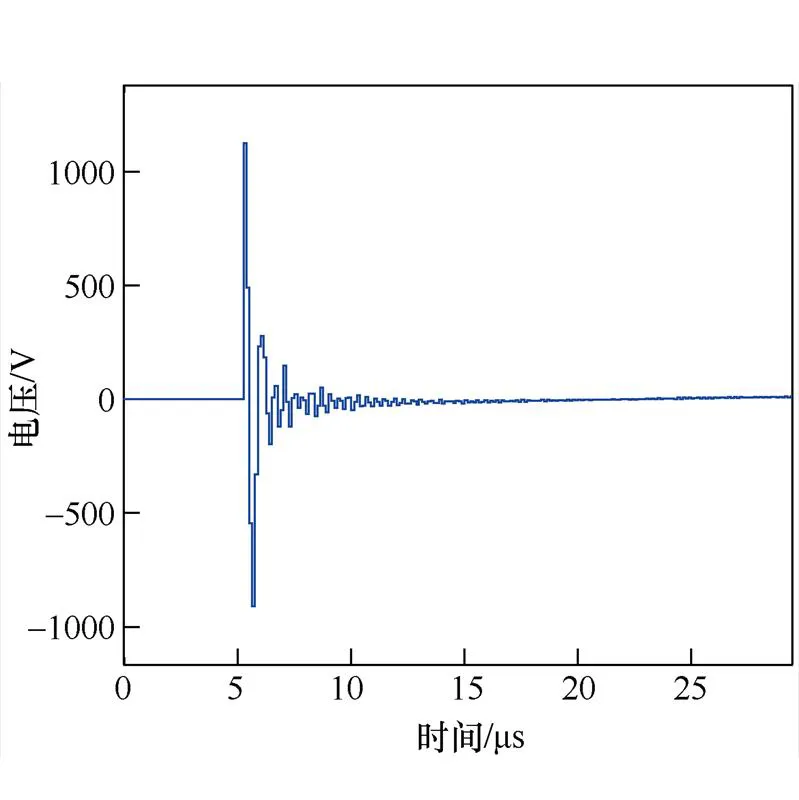
图10 合闸相位为144°时的VCB合闸浪涌过电压波形

3 试验验证与分析

为验证以上分析的准确性，本文对列车浪涌过电压进行现场监测。车体浪涌测试原理如图11所示，FRC—50分压器分别接于车顶接地点A和车底接地点B，使用UNI—T（UPO3240CS）示波器进行数据采集。示波器使用触发模式进行数据采集，触发电压为500mV（对应车体电压800V），采样频率为7MHz。

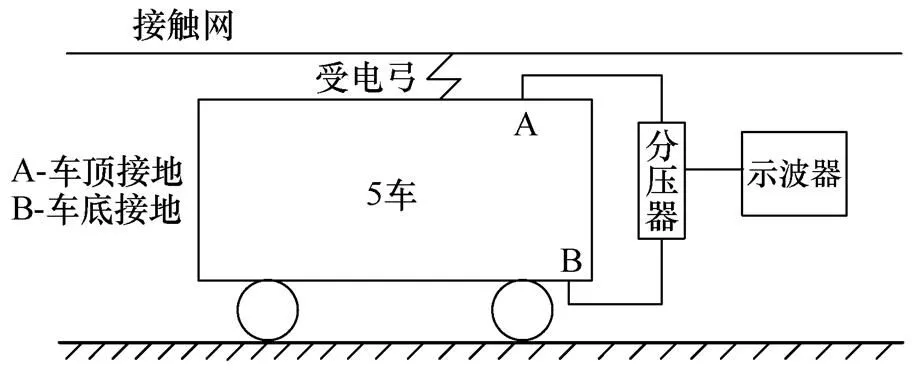
图11 车体浪涌测试原理

按照测试原理连接试验设备与网压互感器，在列车车厢内进行跟车试验，现场测试如图12所示。

图12 现场测试

列车经电分相、交直转换段进入交流区段时，采集到的浪涌过电压如图13所示。

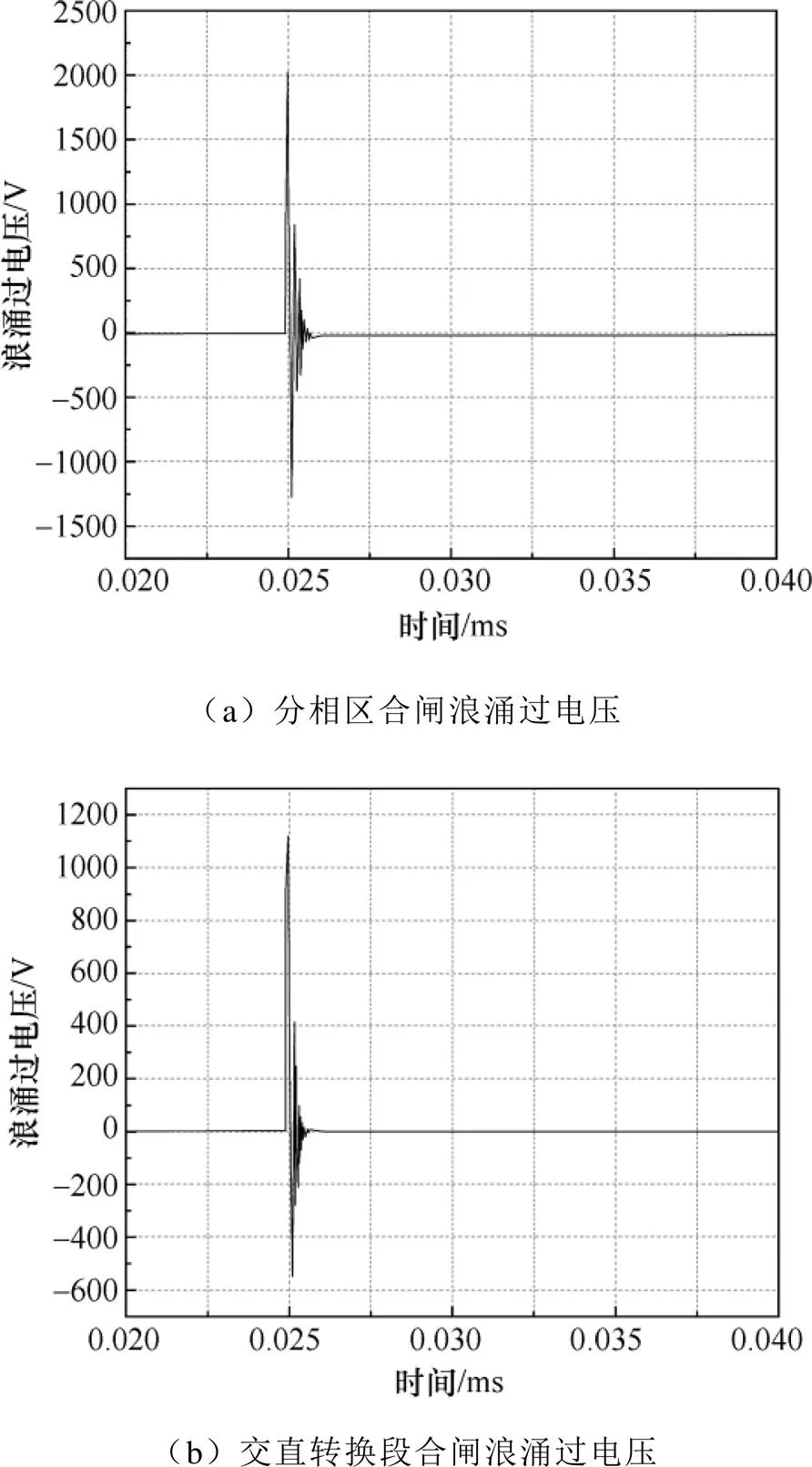
图13 现场采集的浪涌过电压

计算模型仿真与Simulink模型仿真所得浪涌过电压幅值分别为2 330V和2 003.4V并在5ms左右衰减为0V，对比实测结果2 000V且在2.5ms内衰减为0V，本文模型误差率分别为17%和0.15%，由此可见，浪涌过电压幅值存在差别的原因为VCB合闸时的电源电压相位、列车位置不同。

为进一步验证本文模型的合理性及可行性，将仿真及实测信号进行短时剖分，通过Matlab的spectrogram函数对车体浪涌仿真数据和实测数据进行短时傅里叶变换（short-time Fourier transform, STFT），对比合闸相位90°时的浪涌主要波段频谱图。浪涌频谱分析如图14所示。

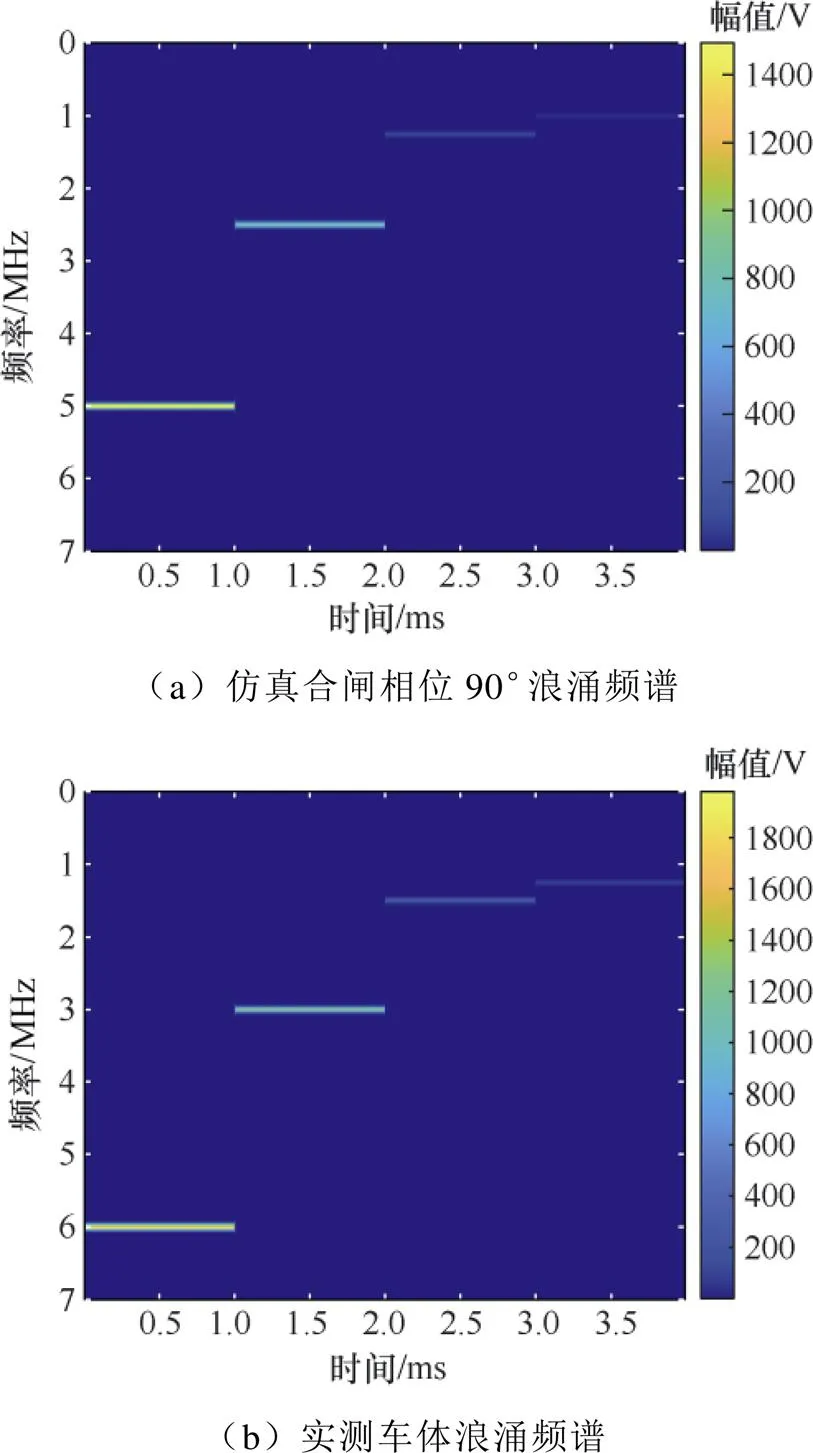
图14 浪涌频谱分析

仿真数据主要波段的频率和幅值分别为5MHz/2 000V、2.5MHz/1 500V、1.25MHz/500V和1MHz/300V，实测数据主要波段的频率和幅值分别为6MHz/2 003V、3MHz/1 400V、1.5MHz/800V和1.25MHz/500V。由此可见，车体浪涌仿真波形与实测波形、衰减时间基本契合，验证了本文分析的正确性和本文模型的可行性。

4 结论

本文研究了双制式列车断路器合闸产生浪涌过电压的机理，并对浪涌过电压进行了仿真分析和现场实测。研究结果表明，双制式列车在通过电分相和交直流转换段后闭合VCB时产生车体浪涌过电压。浪涌过电压幅值主要与列车合闸相位（即合闸时刻的网压值）、牵引所等效参数及高压电缆等效参数有关，其幅值最大可达到2 000V，并且在5ms内逐渐衰减至0V。

[1] 万玉苏, 刘耀银, 高国强. 接地方式对高速动车组升弓浪涌过电压的影响[J]. 铁道学报, 2017, 39(12): 32-37.

[2] 杨帅, 曹保江, 高国强, 等. 高速动车组降弓浪涌过电压分析[J]. 铁道学报, 2015, 37(7): 46-50.

[3] 霍达. 动车组升降弓车体浪涌过电压分布研究[D]. 成都: 西南交通大学, 2018.

[4] 杨盼奎, 贾步超. 接地电阻器对升降弓车体浪涌过电压的影响[J]. 电气化铁道, 2018, 29(1): 84-87.

[5] 吴颢. 车体浪涌过电压研究[D]. 成都: 西南交通大学, 2013.

[6] 冉旺, 李雄, 刘冰, 等. 地面自动过分相中开关切换的瞬态过程研究[J]. 电工技术学报, 2011, 26(11): 150-154, 167.

[7] 陈明忠. 电气化铁道供电系统几种典型过电压的分析与比较[J]. 电气技术, 2014, 15(5): 101-104.

[8] HATSUKADE S, 周贤全. 降低AC车辆车体浪涌电压的方法[J]. 国外铁道车辆, 2010, 47(6): 11-16.

[9] 刘炜, 杨凌云, 马庆安, 等. 双制式列车接地系统的车-地联合牵引供电计算[J/OL]. 西南交通大学学报, http://kns.cnki.net/kcms/detail/51.1277.U.20230111. 1551.003.html.

[10] 陈民武, 付浩纯, 谢崇豪, 等. 交直流双制式牵引供电系统钢轨电位特性分析[J]. 西南交通大学学报, 2022, 57(4): 729-736.

[11] 刘卫东, 胥伟, 刘飞, 等. 交直流双制式列车过分相暂态过程仿真研究[J]. 城市轨道交通研究, 2022, 25(7): 85-89.

[12] 金鑫, 张明锐. 固态断路器过电压分析[J]. 电气技术, 2010, 11(11): 18-22.

Research on circuit-breaker closing surge overvoltage of dual-system train

LI Xuefei1SUN Wenbin1LI Mingze2MA Qing’an3DAI Jun3

(1. CRRC Changchun Railway Vehicle Co., Ltd, Changchun 130062;2. School of Automation and Information Engineering, Sichuan University of Science & Engineering, Yibin, Sichuan 644000;3. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611730)

When a dual-system train passes through the neutral-section, the catenary voltage is coupled to the vehicle body through the high voltage cable distribution capacitance, resulting in a surge overvoltage in the vehicle body, which may seriously threaten the safe operation of the on-board electronic equipment. In this paper, the generation mechanism of the circuit-breaker closing overvoltage of the dual-system train is analyzed. In order to avoid the solution of higher-order differential equations, the overvoltage is decomposed into two oscillation modes. A Simulink model is built to analyze the closing transient process of the dual-system train. On-site measurement of surge overvoltage is also conducted. The theoretical and on-site measurement results are consistent. Studies show that a surge overvoltage of up to 2 000V on the vehicle body maybe be generated and it will decays to zero within about 5 microseconds. The error rates of the calculation model, simulation model, and measured data are 17% and 0.15%, respectively. Therefore, the model proposed in this paper has high feasibility.

dual-system train; surge overvoltage; high voltage cable; capacitive coupling

2023-05-15

2023-06-13

李雪飞（1978—），女，正高级工程师，从事车辆总体设计工作。