实例加权的隐朴素贝叶斯算法在学生成绩预测中的应用

王 狄，余良俊

（1.湖北师范大学 计算机与信息工程学院，湖北 黄石 435002；2.湖北第二师范学院 计算机学院，武汉 430205）

1 引言

近年来，学生的成绩预测逐渐引起广泛关注。学生的期末成绩具有重要意义且在总评中占据显著比重，因此准确预测这一结果变得尤为必要。通过采用适当的模型进行学生成绩预测，不仅可以激发学生的学习兴趣，还能减轻教师的教学负担，实现更有针对性的教学策略。这不仅提升了教学质量，也对学生和教师都具有重要意义。

随着信息技术的发展，越来越多的学者把工作重点放到研究学生成绩预测上面来。目前对成绩预测的研究大致可以分为两类：一类是基于机器学习算法，如决策树[1]，大数据神经网络[2]，贝叶斯网络[3]等，用以预测影响学生成绩的因素；另一类是应用推荐技术，如融合时间序列和协同过滤[4]，融合知识图谱和协同过滤[5]的方法。这两种方法各有优缺点，其中后者在缺乏历史数据的情况下得到的结果往往比较差。朴素贝叶斯算法具有坚实的数学基础，分类效率比较稳定，且对缺失数据不太敏感。[6]因此本文采用的是一种改进的朴素贝叶斯算法来对学生的成绩进行预测，并且和几种经典的朴素贝叶斯改进算法模型进行对比，能够为广大研究者提供一个参考依据。

隐朴素贝叶斯算法（HNB）[7]认为每个属性节点都有一个隐藏的父亲节点，这个隐藏的父亲节点包含了其它属性节点对该属性节点的影响；平均一依赖估测器算法（AODE）[8]是一种特殊的树扩展的朴素贝叶斯算法，它把它的属性节点当成是其它所有属性节点的父亲节点，然后再把这些树扩展的朴素贝叶斯分类器进行平均；实例加权的朴素贝叶斯算法（AVFWNB）[9]是一种对朴素贝叶斯进行实例加权从而改进朴素贝叶斯的算法，该算法通过计算实例的属性值频率来求出每个实例所占的权重，从而对每个实例进行加权。

朴素贝叶斯算法结构简单，且分类效果良好，因此受到了广大研究者的青睐。朴素贝叶斯算法在多个领域都具有很好的应用价值。目前，朴素贝叶斯被广泛应用于文本分类[10]、火灾预警[11]、入侵检测[12]、风险评估[13]等应用领域。

2 改进的朴素贝叶斯算法

2.1 隐朴素贝叶斯模型

隐朴素贝叶斯HNB（Hidden Naïve Bayes）模型通过为每个属性节点添加一个隐藏的父亲节点，这个隐藏的父亲节点对该属性节点的影响包含了其他所有属性节点对该属性节点的影响。[14]假设用A1,A2,A3,A4来表示它的四个属性节点，则隐朴素贝叶斯的结构可以由图1表示：

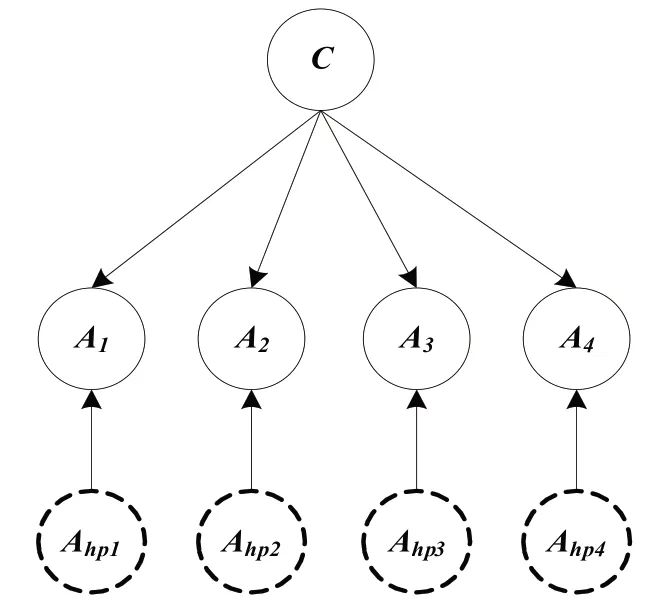
图1 隐朴素贝叶斯网络结构图

在图2中，A1,A2,A3,A4表示的是四个属性变量，C表示的是类变量。每个属性节点都有一个隐藏的父亲节点，隐藏的父亲节点用虚线表示，用于区分其它存在的实际节点。给定一个测试实例x=＜a1,a2,…,am＞，它的分类公式为：

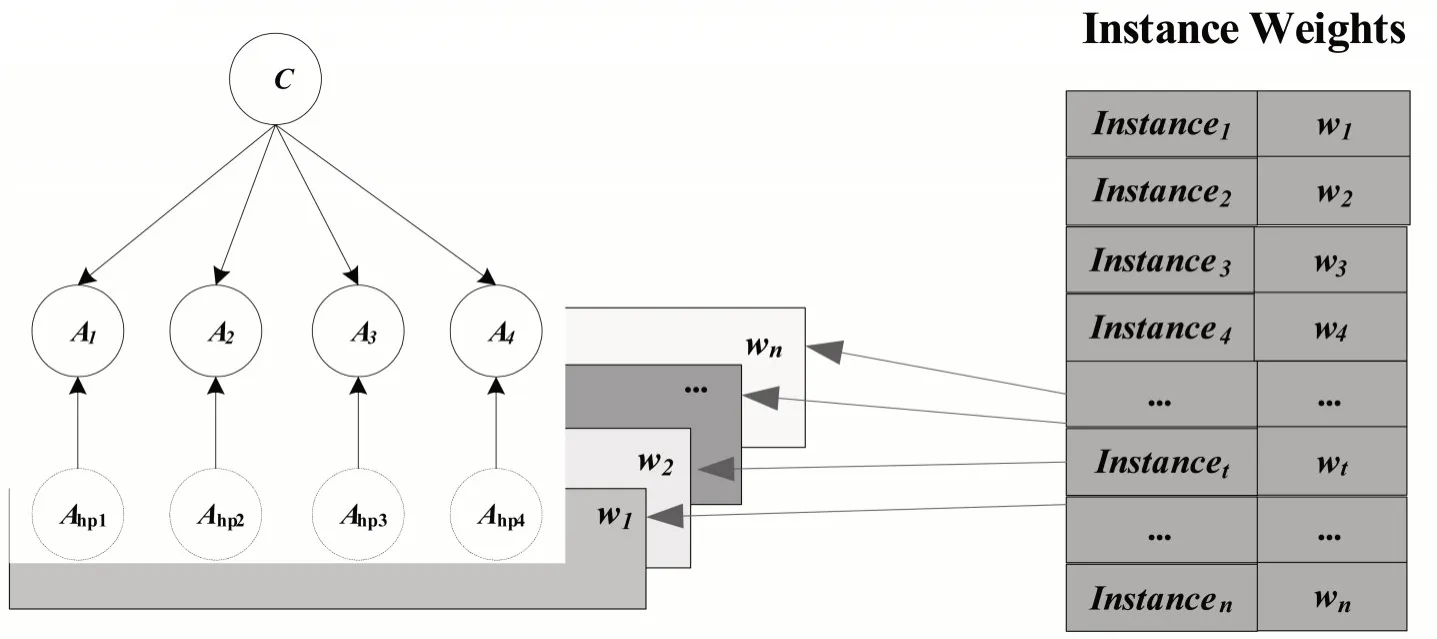
图2 实例加权的隐朴素贝叶斯网络结构图

公式2中P(c)和P(ai|ahpi,c)的计算方式分别用公式3和公式4来计算：

公式3中q表示的是类标记的个数，n表示的是训练实力的个数。公式4中Wij表示的是其它属性节点对该属性节点产生的影响所占的权重。Wij的计算方式用公式5来计算：

公式5中Ip(Ai;Aj|c)表示的是属性变量Ai和属性变量Aj之间的条件相互信息，Ip(Ai;Aj|c)的计算公式为：

公式6中P(ai|c)和P(aj|c)以及条件概率P(ai,aj|c)的计算公式为：

其中ati表示第t个训练实例的第i个属性值，ni表示的是第i个属性值的个数，ct表示的是第t个实例的类标记，δ（）是一个二值函数，当两个变量相等时值为1，两个变量不等时值为0。

在HNB模型中，它的每个隐藏的父亲节点中都包含了其它所有属性节点对该节点的影响。HNB避免了结构学习的复杂性，但是它认为每个实例对分类的影响是相同的。

2.2 实例加权的隐朴素贝叶斯模型

实例加权的隐朴素贝叶斯IWHNB（Instance Weighted Hidden Naive Bayes）模型[15]通过对隐朴素贝叶斯算法进行实例加权，考虑不同实例对分类结果的影响也不同，对每个实例计算不同的权值，一定程度上提高了隐朴素贝叶斯算法的分类性能。假设用A1,A2,A3,A4来表示它的四个属性节点，则实例加权的隐朴素贝叶斯的结构可以由图2表示：

在图3中，w1,w2,…,wn表示的是n个不同训练实例的权值。本文假设其属性变量的个数为四个，分别为A1,A2,A3,A4，虚线部分表示的是每个属性节点对应的隐藏的父亲节点，其隐藏父亲节点的个数也是四个，分别是Ahp1,Ahp2,Ahp3,Ahp4。该模型和隐朴素贝叶斯模型不同的是该模型在建模的过程中为每个实例都分配了不同的权值，再将实例的权值嵌入到分类器中，从而体现不同实例对分类结果的影响。本算法是在已有算法的基础上进行实例加权，将实例加权与结构扩展方法相结合，有效提升了分类器的分类性能。

在实例加权的隐朴素贝叶斯模型中，给定一个测试实例x=＜a1,a2,…,am＞，它的分类公式为：

从公式10中可以看出，实例加权的隐朴素贝叶斯分类器的分类公式和隐朴素贝叶斯分类器的分类公式是相同的，但是在计算P(c)和P(ai|ahpi,c)概率时是不同的。这里是将实例的权重嵌入到隐藏的父亲节点中，则它的先验概率P(c)可以重新定义为：

其中wt表示的是第t个训练实例的权值。条件概率P(ai|c)被重新定义为：

条件概率P(ai,aj|c)被重新定义为：

文章采用了一种基于属性值频率的方式来度量实力的权值。用fti表示属性值ati（第t个实例的第i个属性值）出现的频率，wt表示第t个实例的权值。计算公式为：

其中＜n1,n2,…,nm＞表示属性值的个数向量。

3 实例加权的隐朴素贝叶斯算法的应用

在本节中，采用了美国加州大学欧文分校（UCI）提供的机器学习数据库库中选取的关于教育类的数据集，目前已有622个数据集，数目还在不断增加，是目前常用的一个标准测试数据集。[16]本文采用的是有关于学生成绩预测的教育类数据集，对数据集进行离散化处理、替换属性缺失值、移除无用属性等方法对数据进行预处理，将处理好的数据运用实例加权的隐朴素贝叶斯模型进行分类，同时选取了几种经典的改进的贝叶斯模型来进行对比分析。

3.1 数据集介绍

该数据采集自葡萄牙学校两所中学教育学生成绩。该数据共有649个实例，33个属性。数据集记录的是学生葡萄牙语的成绩。其中第二阶段成绩G2存在部分数据缺失的情况，目标属性G3与属性G2和G1具有很强的相关性。这是因为G3是最终成绩，G1和G2对应的是第一阶段和第二阶段的学生成绩。给定的部分学生成绩数据集如表1所示：

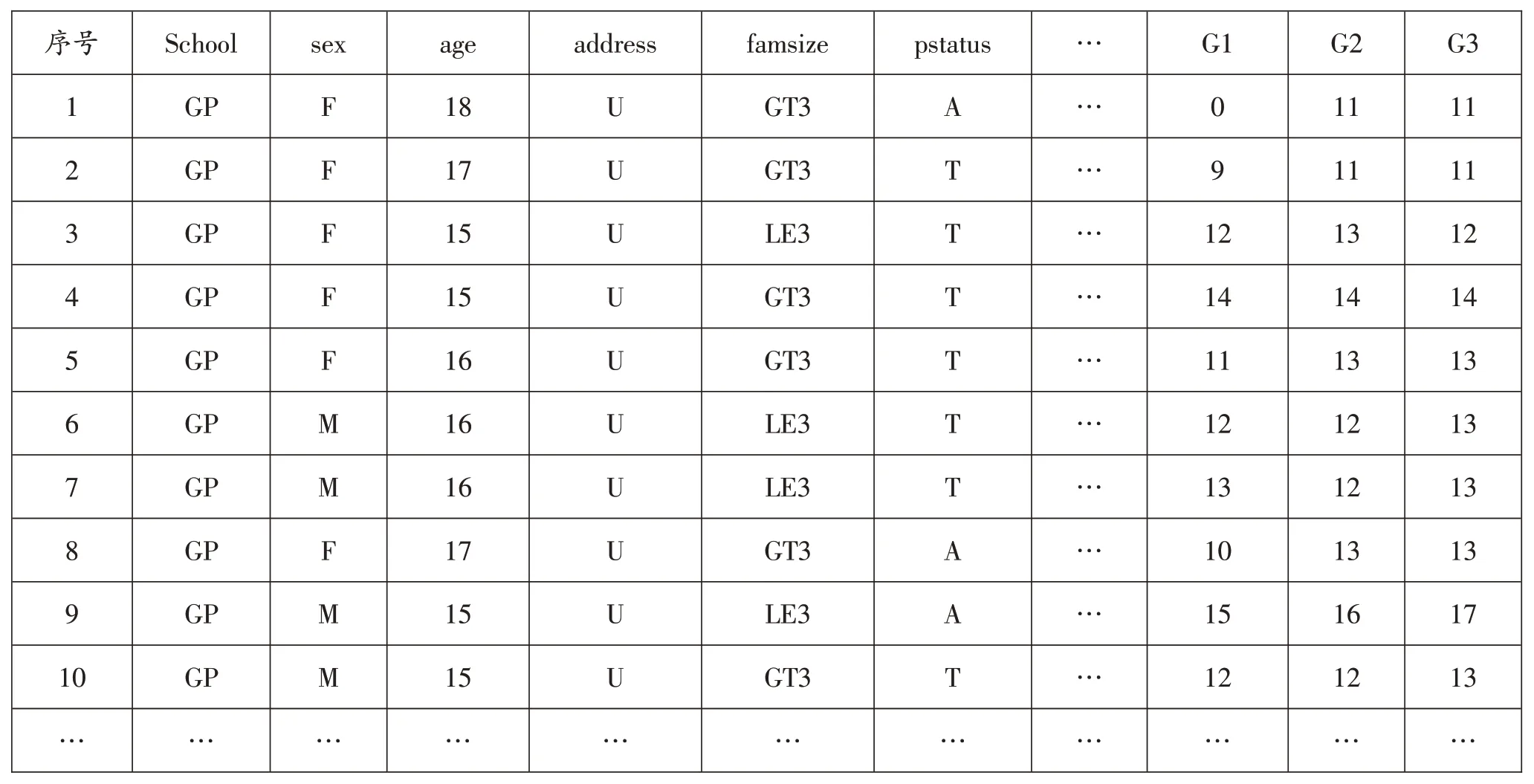
表1 部分学生成绩数据集

预处理后的学生成绩数据集如表2所示：

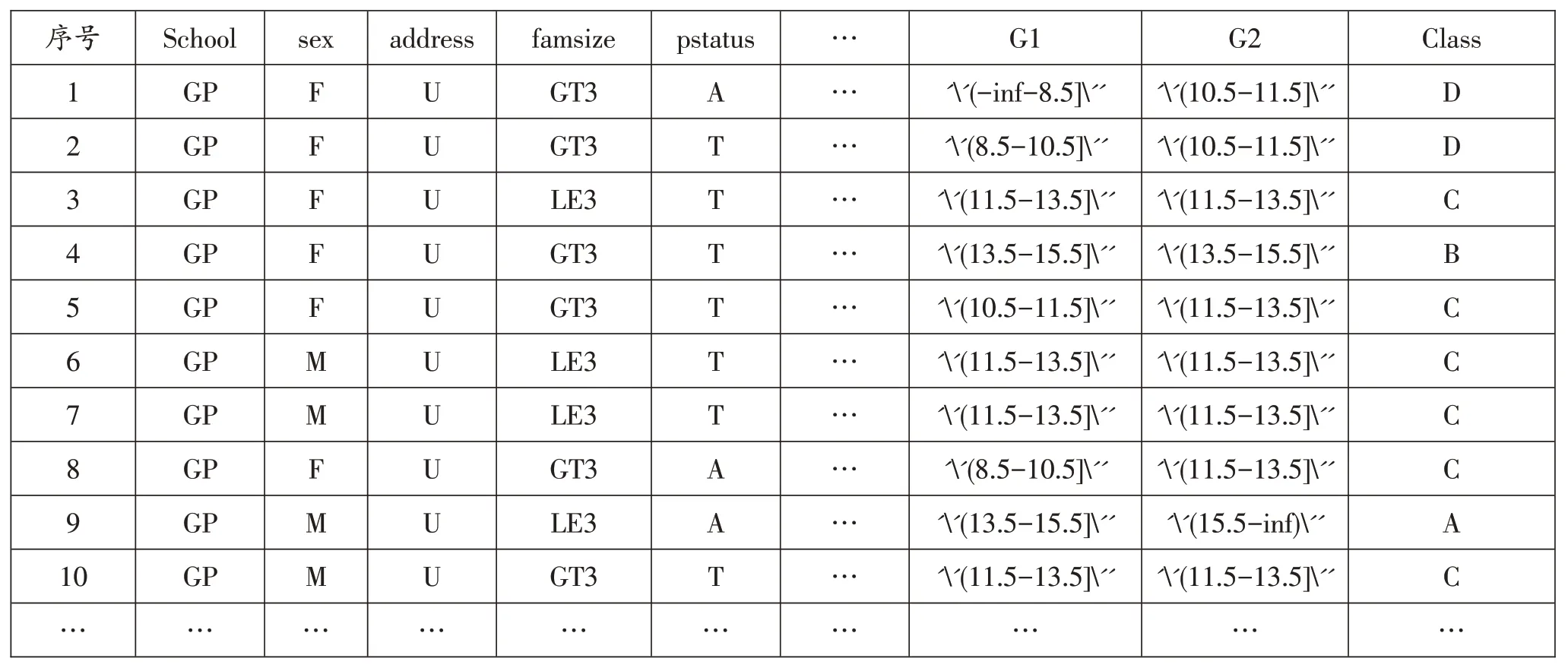
表2 预处理后的学生成绩数据集

本文将学生成绩分为五类：20 ≥成绩≥16 时为A；15 ≥成绩≥14 时为B；13 ≥成绩≥12 时为C；10 ≥成绩≥11时为D；0 ≥成绩≥9 时为E。对应的表格如表3所示：

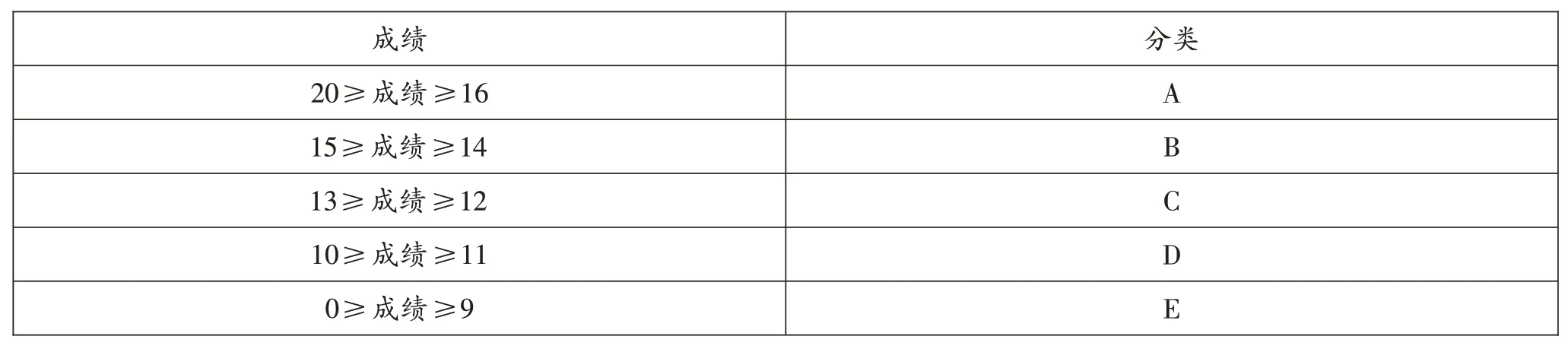
表3 成绩分类表

3.2 实验过程

3.2.1 数据预处理

本文使用的数据集是从UCI 官网下载的有关教育方面的数据集，有649 个实例和33 个属性。数据集为csv格式的数据，不同属性之间由分号分开。在处理数据时先将数据分成33个列。其中G3属性为学生最终考试的成绩，因此本文根据G3列中的值和表3成绩分类表来给每条数据打上标记来替换G3列中的值，并将G3列名修改为Class，Class即为标签列。

预处理过程中，本研究使用了国际数据挖掘weka平台。首先，由于本数据集的G2属性所在的列存在缺失值，于是使用了weka平台提供的无监督过滤器Replace Missing Values 来替换缺失值，该方法是通过用缺失值所在列的平均值来对缺失值进行替换。对于数据集中存在的无用的属性，如：age属性，本文使用了weka平台提供的无监督过滤器Remove 对其进行删除。数据集中还存在一些连续的数值型的属性值，如：G1，G2 属性，不利于文本的分类，因此要对其进行离散化处理，本文采用了weka平台提供的有监督过滤器Discretize对数值型的数据进行离散化处理，从而减弱极端值和异常值对数据的影响。

3.2.2 实例加权的隐朴素贝叶斯算法实现

在数据处理完毕后，在eclipse 开发环境中使用Java 语言对实例加权的隐朴素贝叶斯算法进行复现。实现过程包括以下几个步骤：

（1）计算属性值频率和实例权重。在实例加权的隐朴素贝叶斯算法中，首要任务是准备数据并计算相关属性的频率。对于每个属性，计算它在整个数据集中的出现频率。这为后续的条件概率计算提供了基础。同时，本研究根据属性值的频率为每个实例计算一个权重。这些权重用于调整训练过程中实例的影响力，以确保模型更关注对分类起关键作用的实例。

（2）构建一个条件概率表。条件概率表是实例加权隐朴素贝叶斯算法的核心组成部分。为了构建这张表，本文从训练数据中计算每个属性在不同类别条件下的条件概率，为每个属性值计算在特定类别下的频率。然后，这些频率被转化为条件概率，从而能够在预测过程中根据属性值进行分类。为了防止概率为零的情况，本研究还应用了拉普拉斯平滑技术。

（3）模型参数训练。模型参数的训练是使得算法能够更好地预测新实例的关键步骤。本文根据计算得到的实例权重和条件概率进行模型参数的训练。这些参数包括类别的先验概率以及每个属性在不同类别条件下的条件概率。通过考虑权重和概率，能够建立一个适应不同实例特点的模型。

在预测阶段，本文将训练得到的模型参数应用于新的学生实例。对于一个新的实例，计算其属于每个类别的概率，并选取具有最高概率的类别作为预测的学生成绩类别。这个过程充分利用了模型参数和条件概率表，使得本研究能够基于数据来进行准确的预测。

为了评估实例加权的隐朴素贝叶斯算法在学生成绩预测方面的性能，本文使用了测试数据集。通过将模型应用于测试数据集，可以计算出预测结果并与实际结果进行比较。本文采用了准确率、召回率、AUC指标[17]以及F-score 指标[18]等多种评估指标，从不同角度评估了模型的性能。这些指标能够揭示模型的分类效果、区分能力以及综合性能，为本文提供了全面的性能评估。

3.2.3 实例加权隐朴素贝叶斯算法在学生成绩预测中的应用

从数据挖掘的角度来分析，学生成绩预测实际上是一个分类问题。类变量的取值有5个：即“A”“B”“C”“D”“E”。数据集中的各种属性就是影响学生成绩的因素，属性的取值不同，最终类标记的取值也会受影响。

朴素贝叶斯网络分类器在进行文本分类时具有较好的分类效果。鉴于目前朴素贝叶斯在教育方面的应用较少，本文将改进的朴素贝叶斯算法应用到教育数据集中，为广大学者在处理教育数据集时提供了一个参考依据。

本文用准确率、召回率、AUC指标和F-score四个指标来对模型进行评估。其中表4为只对数据进行离散化处理后的实验结果，表4为对数据进行离散化处理、删除无用属性以及替换缺失值后的实验结果。

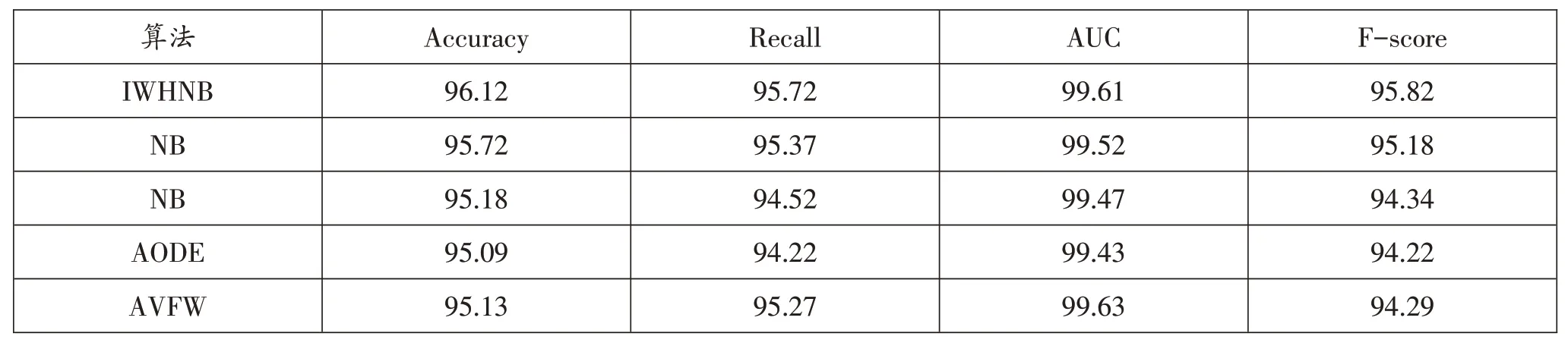
表4 离散化处理后实验结果

从表4 和表5 中可以看出，在经过了无用属性的删除和缺失值的替换后，实验的准确率、AUC 指标和Fscore都有所提高，召回率相较于HNB算法略有降低。

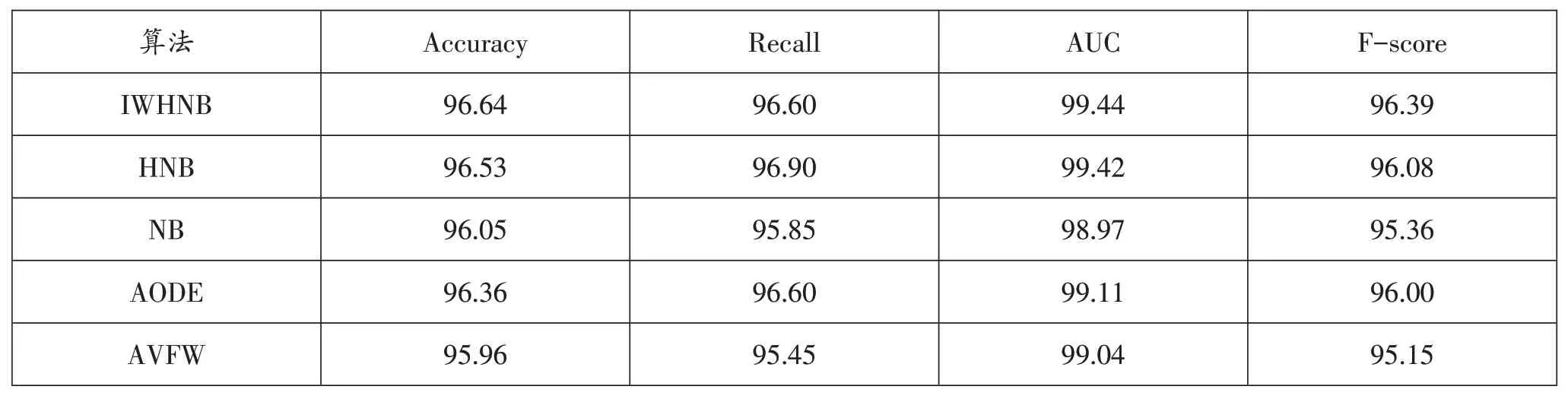
表5 离散化处理、删除无用属性和替换缺失值后实验结果

图4表示的是IWHNB算法和几种改进的朴素贝叶斯算法在教育数据集上对准确率、召回率、AUC指标[17]和F-score 指标[18]进行的对比。准确率是模型正确预测为正类别的样本数量占所有预测为正类别的样本数量的比例，召回率是模型正确预测为正类别的样本数量占实际正类别样本数量的比例，AUC 是ROC 曲线下的面积，用来衡量模型区分正负类别的能力，F-score 综合考虑了准确率和召回率，是一个衡量模型综合性能的指标。

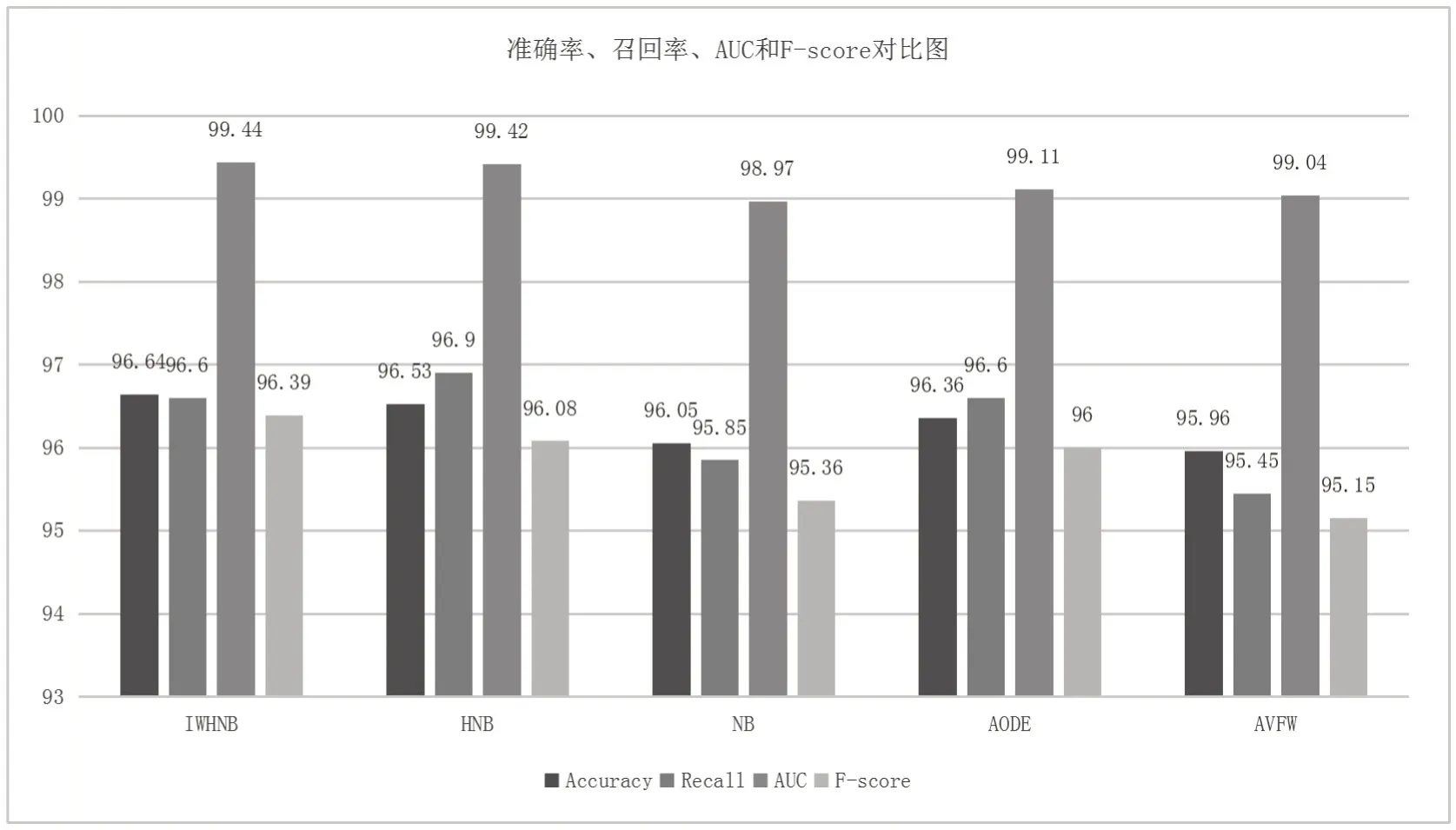
图4 IWHNB算法准确率、召回率、AUC和F-score指标对比图

从图4中可以看出，IWHNB 和HNB 在准确率方面表现最佳，均超过96.5%，说明这两个算法在将正类别样本正确分类方面具有较高的能力。AODE和NB的准确率也超过96%，而AVFW略低于96%。在召回率方面，HNB算法表现最好，达到96.90%，这意味着HNB在正确预测实际正类别样本的能力上表现优异。IWHNB和AODE的召回率也很高，达到96.60%。NB和AVFW的召回率稍低。在AUC指标上，IWHNB和HNB在AUC上表现最佳，分别达到99.44%和99.42%。AODE和AVFW也具有很高的AUC值，分别为99.11%和99.04%，而NB 稍低。在F-score 指标上，IWHNB 和AODE 的F-score 最高，分别为96.39%和96.00%。HNB、NB 和AVFW的F-score稍低。

综合上述结果，IWHNB和HNB在多个指标上表现出色，既有较高的准确率和召回率，又具备优越的AUC和F-score。AODE在召回率和AUC上也表现良好。NB的性能在各项指标上均属于中等水平，而AVFW在整体上稍逊。

4 结语

在本研究中，针对学生期末成绩预测过程中的问题，本研究采用了实例加权的隐朴素贝叶斯算法对学生期末成绩进行预测。通过实验结果显示，成功实现了对学生成绩的高准确率预测。本文选取了葡萄牙两所中学的教育成绩作为数据集，在数据预处理阶段，本文有效地处理了缺失值，剔除了无用属性，并对数值属性进行了离散化处理。这项研究不仅在预测准确率方面取得了成功，还有助于减轻教师和学生的工作压力，提高教学效率，实现针对性教学。本文特别采用了实例加权的隐朴素贝叶斯算法，相较于其他改进的贝叶斯算法，表现出更高的预测准确率。这一结果充分证明了本方法的可行性。在未来的研究中，将重点考虑与其他算法的对比实验，以更全面地评估研究方法的性能。本研究为学生成绩预测领域提供了有价值的见解，并为进一步探索和优化预测算法提供了方向。这项工作将有助于教育领域的决策制定和教学改进，也将为机器学习在教育中的应用提供新的思路。