一元线性回归模型在教育经济预测中的应用
吴新林,陈诗雨
(1.湖北第二师范学院 数学与统计学院,武汉 430205;2.湖北第二师范学院 大数据建模与智能计算研究所,武汉 430205)
1 引言
教育经费的增加与中国国内生产总值增加有关,经济发展水平是教育发展水平的直接和最终决定因素,是现代教育的根本性的社会动力。增加教育经费可以为教育提供物质条件和基础,这意味着将会有更多资源流向教育,可以建设更完善的教育设施,招聘更优秀的教师,从而提高教育产出。通过预测教育经费可帮助人们做出合理决策,及时调整教育资源中的分配结构。在研究预测的过程中需要用到数理统计的相关方法,如,李海娟分析了数理统计在经济学中应用的意义以及具体的应用策略[1],为本研究提供了参考。
本文着眼于利用一元线性回归模型预测教育经费,研究国内生产总值与教育经费的关系,引入一元线性回归模型,为今后的预测提供解决思路和方法步骤。对一元线性回归模型进行预测的研究主要分为两部分,一部分为研究预测过程中模型的相关概念与基本理论、模型的建立与方法步骤,其中,茆诗松等给出了回归系数的最小二乘估计,通过求偏导数并命其为0 可以得到参数的最小二乘估计算式[2];李文亮等以济源市1991-2000年国内生产总值与固定资产投资关系为例将一元线性回归模型在投资方面的预测中具体进行了应用,并展示了一元线性相关关系判定中的相关图和相关系数这两种方法[3];何福云等将一元线性回归模型在预测工程项目的造价中进行应用[4];杜克余等将一元线性回归在分析农业建设规模中进行运用。[5]唐亚宁等[6]对一元线性回归方程的三种显著性检验的等价性进行分析;另一部分为利用软件对一元线性回归模型进行求解和预测;张海燕等将Excel软件应用到一元线性回归问题的求解中。[7]随着研究的深入,郭志军等应用Excel软件对一元线性回归模型进行分析,得出数据间的关系,建立回归方程[8];杨雄等以成本预测为案例,应用Excel 对案例进行回归方程求解,并对Excel 运行结果中的各参数进行解释。[9]综合以上分析可以看出,各学者将一元线性回归模型应用于不同研究领域,本文一方面结合2012-2021年期间国内生产总值与全国教育经费的样本数据对一元线性回归模型进行了参数估计,并对结果进行了显著性检验,另一方面,将建立的模型应用于教育经济预测问题中,借助Excel软件对模型进行了求解。
2 一元线性回归模型
2.1 一元线性相关关系的判定
一元线性回归模型使用的条件是两个经济变量之间需要存在线性相关关系,下面将介绍两种判断经济变量之间是否存在线性相关关系的方法。
方法1:散点图法
调查并收集具有相关关系的两个现象的相关资料及数据,形成一组组成对的数据并在直角坐标系中呈现。观察这些点的分布情况,如果这些点大致分布在一条直线上下,就说明这两个变量之间有线性关系,如果这些点散落分布,不在一条直线附近,说明这两个变量之间不是线性相关。
方法2:相关系数
通过计算相关系数也可以来确定相关关系,计算公式为:[2]
2.2 一元线性回归模型及其估计
在确定了两个变量之间有线性相关关系后,就可以进行线性回归分析。设一元线性回归模型为ŷ=â+b̂x,称y关于x的回归方程[2],所呈现的图形称为回归直线。给定x=x0后,称ŷ0=â+b̂x0为预测值。
一般采用最小二乘法估计模型中的â,b̂,令存在â,b̂使得Q(a,b)最小,将Q(a,b) 分别对a,b进行求偏导并命其为0。解得:
这就是参数的最小二乘估计,其中:[2]
2.3 回归方程的显著性检验
下面需要判断本文所使用的回归方程是否有意义,本文采用F检验法对回归方程进行检验。
在F检验中[2]:称ŷi=â+b̂xi为xi处的回归值,又称yi-ŷi为xi处的残差。数据总的波动用总偏差平方和表示:。yi的波动用回归平方和表示:。y的观测值与回归值之间的差距用残差平方和表示:
F 作为检验问题的检验统计量[2]:,对于整个给定的显著性水平α,其拒绝域为F≥F1-α(1,n-2) ,整个检验也可列成一张方差分析表,如表1所示,检验也可用p值进行。

表1 方差分析表
3 一元线性回归模型在教育经济预测中的应用
选取2012-2021年中国国内生产总值和全国教育经费数据(如表2所示),建立一元线性回归模型。中国统计年鉴数据显示,2022年国内生产总值为121.0万亿元,下面利用一元线性回归模型和2022年国内生产总值预测2022年全国教育经费。(注:截至2023年5月,2022年度全国教育经费数据尚未官方公布。)
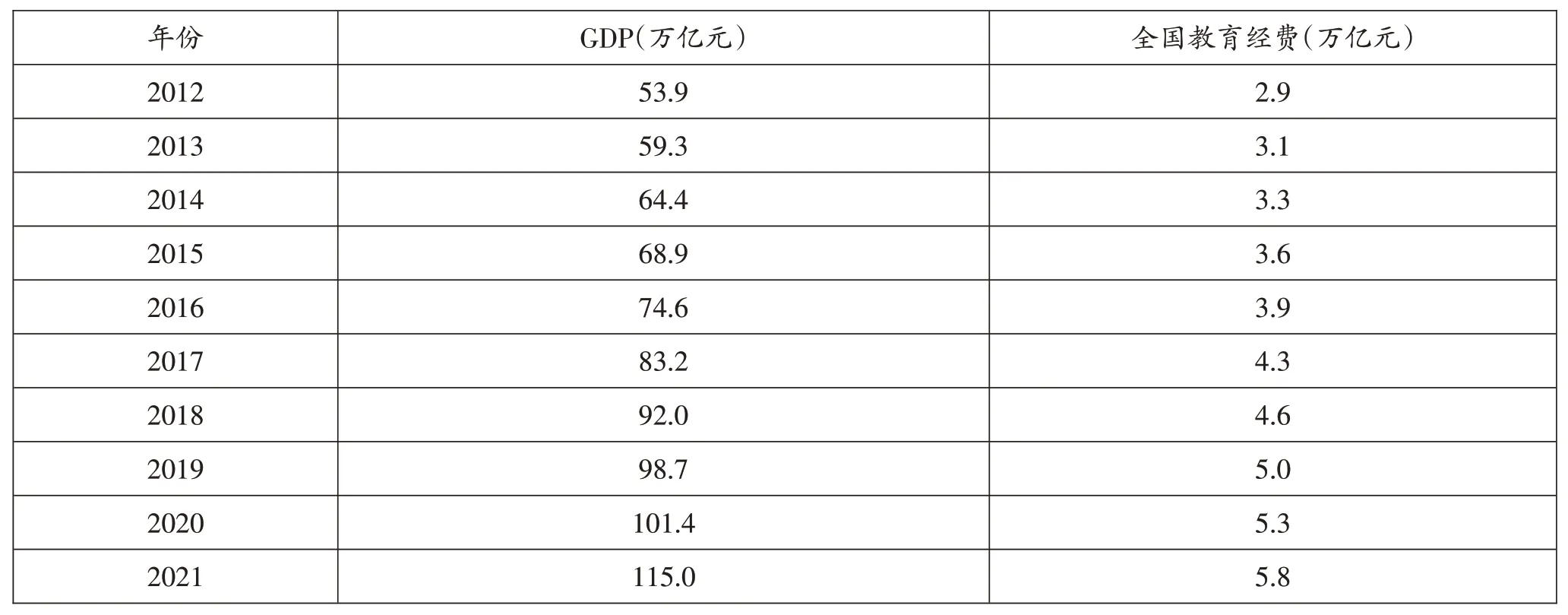
表2 2012-2021年GDP和全国教育经费
(1)一元线性相关关系的判定
方法1:绘制散点图
由表2中2012-2021年中国国内生产总值和全国教育经费数据绘制散点图,如图1所示:
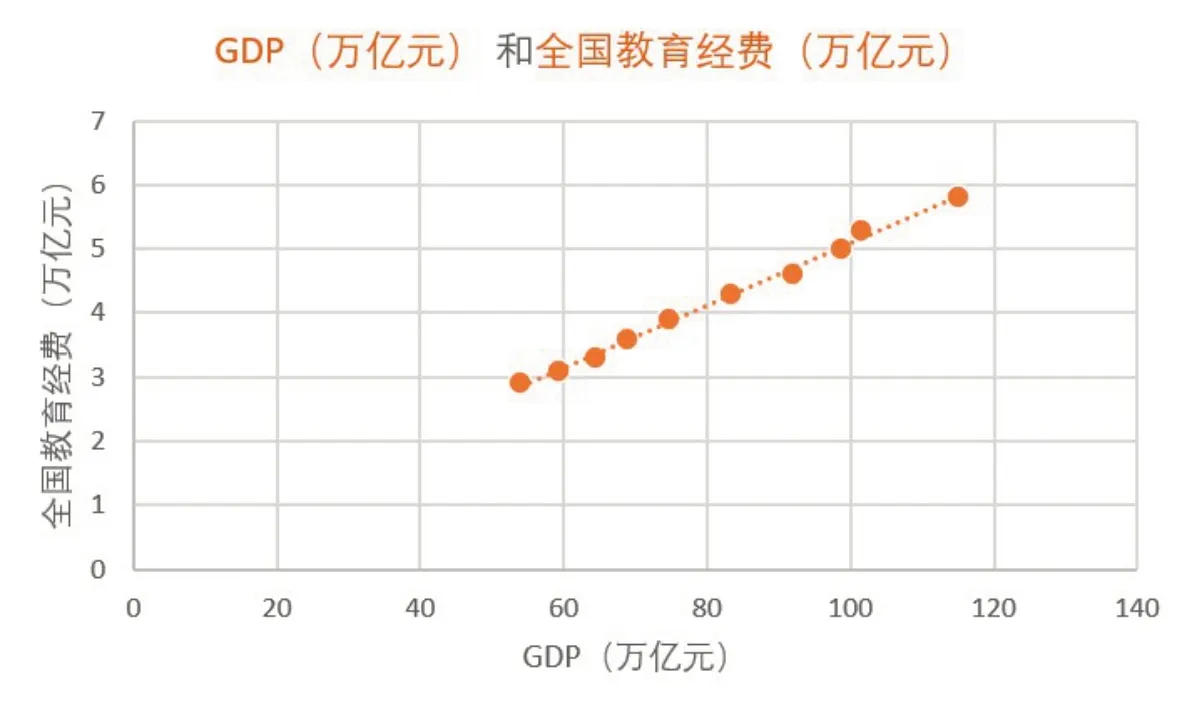
图1 GDP和全国教育经费散点图
方法2:计算相关系数
由相关图(见图1)和相关系数(0.998)可以判断中国国内生产总值与全国教育经费之间存在高度的线性相关关系。
(2)建立一元线性回归模型
从散点图我们发现10个点基本在一条直线附近,这说明两个变量之间存在线性相关关系,我们设关于中国国内生产总值与全国教育经费之间的一元线性回归模型为:ŷ=â+b̂x,其中,â、b̂为待求的回归系数。
(3)最小二乘估计求回归系数
(4)回归方程的显著性检验
这里我们考虑关于回归方程的显著性检验,相关指标计算结果如下:
将数据移入方差分析表,继续进行计算。计算出国内生产总值和全国教育经费的方差分析表,如表3所示。因为p值很小,故在显著性水平0.01下回归方程是显著的。

表3 GDP和全国教育经费回归方程的方差分析表
(5)预测
建立好模型后就可以进行预测,将每年的国内生产总值代入回归预测模型中可以得到全国教育经费的预测值。由中国统计年鉴得知,2022年的国内生产总值为121.0万亿元,则2022年全国教育经费的预测值为:ŷ=0.15+0.05×121=6.2(万亿元)。
4 用Excel软件求解一元线性回归模型
4.1 Excel求解步骤与方法
Excel 软件是微软公司出品的Office 系列软件中的其中一款,它是一个功能强大的可以进行数据管理与分析的软件,Excel向我们提供了80多个统计函数。本文首先应用Excel软件的SLOPE函数和INTERCEPT函数求出回归方程的斜率和截距,然后应用FORECAST函数进行预测。其具体求解步骤与方法如下:
(1)SLOPE函数:选择“y的范围(因变量)”和“x的范围(自变量)”,计算的回归直线y=a+bx的斜率b。
语法:SLOPE(Known-y's,Known-x's)
(2)INTERCEPT 函数:通过“y的范围(因变量)”和“x的范围(自变量)”,计算回归直线y=a+bx的截距a。
语法:INTERCEPT(Known-y's,Known-x's)
(3)FORECAST函数:通过指定的x值来预测y值。
语法:FORECAST(x,Known-y's,Known-x's)
其中:
X……预测中使用的值;
Known-y's……指定已知的y值;
Known-x's……指定已知的x值。
4.2 应用举例
求解步骤如下:
(1)将2012-2021年中国国内生产总值和全国教育经费的数据输入到Excel中。
(2)在单元格F2中插入SLOPE函数,选出因变量数值区域及自变量数值区域,计算出斜率b=0.05,过程及结果如图2所示。
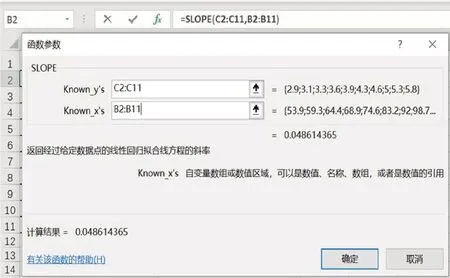
图2 SLOPE函数
(3)在单元格F3中插入INTERCEPT函数,选出因变量数值区域及自变量数值区域,计算出截距a=0.24,过程及结果如图3所示。
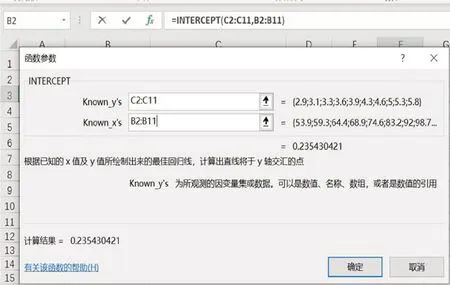
图3 INTERCEPT函数
(4)由斜率b和截距a的值可得,一元线性回归方程为ŷ=0.24+0.05x。
(5)在单元格C12中插入FORECAST函数,在B12中输入2022年国内生产总值为121.0万亿元,选择其为预测中使用的X值,再选出因变量数值区域及自变量数值区域,得到预测值为6.12,过程及结果如图4所示。
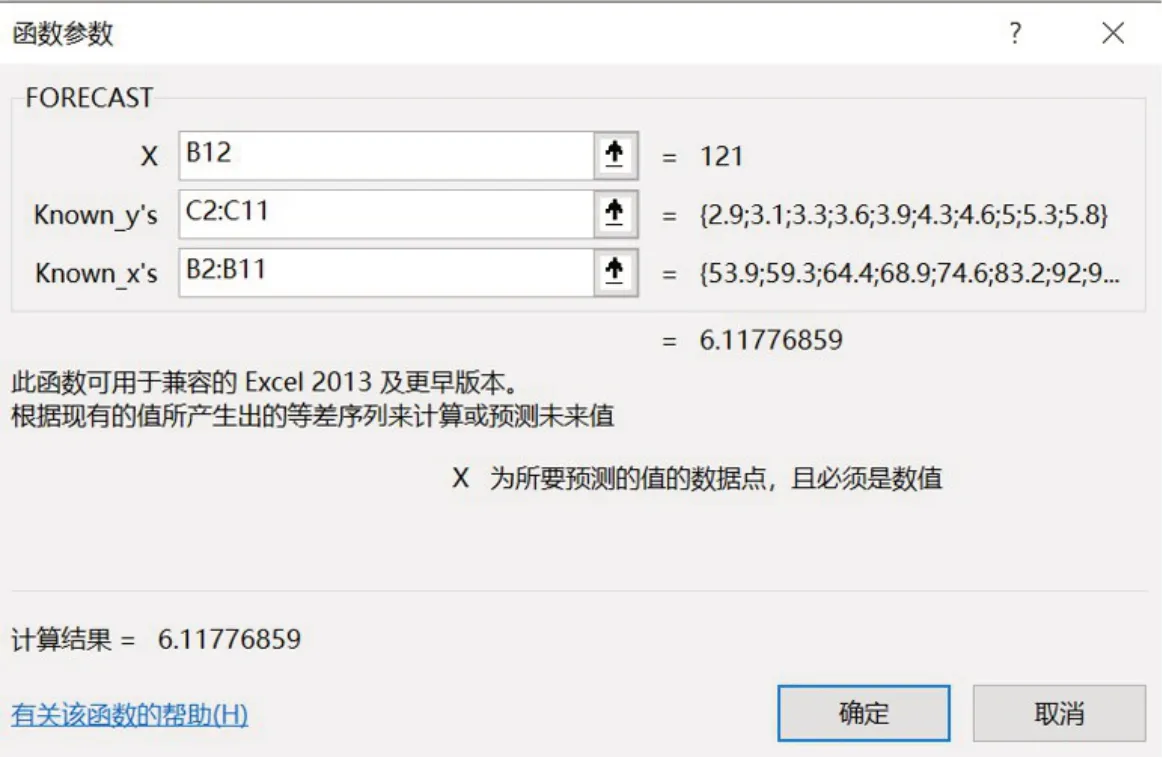
图4 FORECAST函数
5 结论
经济预测是当代社会活动中的一个热点研究问题,具有广泛的应用价值。本文研究回归分析法中的一元线性回归模型,结合国内生产总值与教育经费的相关数据,通过分析国内生产总值与教育经费的相关性建立回归模型并应用Excel 软件对模型进行求解与预测。根据预测结果对教育资源进行合理分配与决策。通过对相关理论的研究及具体实例的计算,给出了求解一元线性回归模型及其预测的详细步骤,实用性较强。结合本文的研究思路,可以进一步将一元线性回归模型应用于投资经济、航空经济、物流经济等不同经济领域,通过预测帮助人们展望未来经济发展前景,做出决策并进行科学管理。

