变量重要性-反向传播人工神经网络辅助激光诱导击穿光谱测定铁矿石中硅、铝、钙和镁含量
刘 曙,金 悦,,苏 飘,,闵 红,安雅睿,吴晓红*
1. 上海海关工业品与原材料检测技术中心,上海 200135 2. 上海理工大学材料与化学学院,上海 200093
引 言
硅、铝、钙和镁含量是铁矿石质量评价的重要指标,影响铁矿石的贸易价格及高炉炼铁工艺[1]。铁矿石中硅(以SiO2计)、铝(以Al2O3计)、钙(以CaO计)和镁(以MgO计)含量的测定方法包括滴定法[2-3]、分光光度法[4]、原子吸收光谱法[5-7]、电感耦合等离子体原子发射光谱法[8]和X射线荧光光谱法[9]等,预处理方法复杂,测试周期长。激光诱导击穿光谱(LIBS)是一种以高能激光脉冲轰击物质表面,获取待测物质元素成分和含量的原子发射光谱技术[10],具有原位、快速、无需复杂的样品制备等优点,在铁矿石成分分析领域受到广泛关注[11]。然而,受制于不同种类铁矿石的基体效应、激光能量波动以及等离子体时空演化的不确定性,激光诱导击穿光谱定量分析铁矿石中元素含量面临测量不确定度高、误差大的严峻挑战[12]。
1991年Grant等[13]使用铁元素作内标,通过每一种元素与铁元素的强度比建立校准曲线,建立了LIBS分析铁矿石中TFe(总铁)、CaO、MgO、SiO2、Al2O3和TiO2含量的方法。受到光谱干扰、自吸收和基体效应的影响,基于单个谱线强度建立的校准曲线有时无法真实反映元素含量,导致分析准确度低。多变量回归分析与LIBS相结合是克服铁矿石LIBS定量分析中基体效应的一种有效途径,2008年Death等[14]利用主成分回归(PCR)与LIBS相结合测定铁矿石中TFe、Al2O3、SiO2、MnO、K2O,预测均方根误差(RMSEP)分别为0.65 wt%、0.53 wt%、0.37 wt%、0.017 wt%。偏最小二乘(PLS)是在PCR基础上发展起来的,通常被认为能提供比PCR更高的预测准确度。2015年Hao等[15]使用PLS与LIBS相结合建立铁矿石中CaO、MgO、Al2O3和SiO2的定量分析模型,RMSEP分别0.036 2 wt%、0.025 8 wt%、0.191 4 wt%和0.281 0 wt%。2018年Guo等[16]采用混合稀疏偏最小二乘(SPLS)建立光谱数据和浓度的多变量线性回归模型,再通过最小二乘支持向量机(LS-SVM)对SPLS回归模型的残差进行拟合,建立铁矿石中CaO、MgO、Al2O3和SiO2的定量分析模型,RMSEP值分别为0.356 9 wt%、0.045 6 wt%、0.096 2 wt%和0.215 7 wt%,与传统的SPLS或LS-SVM模型相比,混合模型SPLS-LS-SVM获得了更好的性能。铁矿石LIBS光谱包含光谱噪声和冗余信息,以上研究工作都是将全光谱作为输入变量,且研究的铁矿石样本数量相对较少,相对于数据饥渴型的机器学习算法而言,容易导致模型过拟合,制约模型的实际应用。
反向传播人工神经网络(BP-ANN)作为一种新兴的多变量分析方法,在高维数据上发挥着重要的优势,既可以处理线性问题,又可以处理非线性问题,已在诸多领域显示出了巨大的潜力[17-19]。将铁矿石LIBS全光谱数据作为BP-ANN模型的输入,容易引发维度灾难,导致模型过拟合,分析准确度偏低。已有研究提出了主成分分析(PCA)[20]、SelectBest[19]等降维或特征选择方法与BP-ANN结合用于待测物质的LIBS分析,说明通过提取LIBS光谱中的有效信息,减小BP-ANN模型的输入变量,能有效提升模型的准确度。变量重要性方法通过数据置换的方式来测量每个输入变量对模型整体预测性能的影响。该方法不仅可以测量每个变量的重要性得分,而且可以衡量变量与变量之间的相互关系。通过计算输入光谱特征的变量重要性,选取一小部分覆盖原始光谱信息的特征变量作为模型输入,可以有效降低冗余变量对模型的干扰[21-22]。Liu等[21]使用变量重要性与随机森林回归(VI-RFR)相结合定量分析聚丙烯中的有毒元素Pb、Cr、Hg,结果显示相比于随机森林回归(RFR)和偏最小二乘回归(PLSR),VI-RFR获得了最低的均方根误差(RMSE)和测定系数(R2)。同年,该课题组在识别和鉴定不同种类的塑料的研究中,将变量重要性与偏最小二乘判别(PLS-DA)相结合构建分类校准模型,相比于RF和VI-RF模型,VI-PLS-DA有着最高的分类准确率(99.55%)和最短的分类时间(0.096 ms)[23]。变量重要性与BP-ANN相结合应用于铁矿石中CaO、MgO、Al2O3和SiO2含量分析尚未报道。
本工作在铁矿石卸货过程中采集并制备了来自4个国家的12个种类244批铁矿石代表性样品,采用商用LIBS仪采集了相关样品的LIBS光谱,探索了LIBS结合VI-BP-ANN定量分析铁矿石中CaO、MgO、Al2O3和SiO2含量的可行性。使用随机森林(RF)对LIBS光谱特征进行重要性测量,通过袋外(OOB)误差优化RF模型参数,变量重要性阈值可控制输入BP-ANN的变量数量。采用五折交叉验证(5-CV)的R2、RMSE优化了模型的预处理方法、变量重要性阈值、神经元个数。为了验证VI-BP-ANN模型的预测能力,PLS、支持向量机(SVM)和RF应用于比对研究。
1 实验部分
1.1 铁矿石样品采集与制备
收集了来自澳大利亚、南非、哈萨克斯坦和智利4个国家共计12个种类244个铁矿石代表性样品,依据GB/T 10322.1—2014制备化学分析试样。有关铁矿类别、样本数量和主要元素含量范围如表1所示。根据GB/T 6730.65—2009测定铁矿石全铁含量,根据GB/T 6730.62—2005测定铁矿石CaO、MgO、Al2O3和SiO2含量,其中TFe的范围为53.26~66.24 wt%,SiO2的范围为1.03~15.66 wt%,Al2O3范围为0.20~3.06 wt%,CaO的范围为0.016~1.768 wt%,MgO范围为0.034~9.900 wt%。在LIBS测量前,使用聚乙烯塑料环对铁矿石粉末样品进行聚拢,并放置在压片机下在30 t的压力下维持30 s压制成饼状,使用洗耳球对表面进行吹扫。

表1 铁矿石类别、数量和主要元素含量范围(wt%)Table 1 Quantity and concentration range of main elements of brand iron ore(wt%)
1.2 LIBS仪器与光谱采集
实验采用商用的LIBS仪器(Chemreveal3764,TSI公司),激光源为调Q的Nd∶YAG激光器,波长1 064 nm,激光能量设置为30 mJ,延迟时间1 μs,频率为5 Hz。为了尽可能降低由于元素浓度分布不均匀和物理性质差异引起的基体效应影响,实验中通过以5×5矩阵的方式进行光谱采集,每个位置进行5次连续激发并累计为一个光谱,将样品表面6个不同的位置矩阵收集的6条LIBS光谱最终平均为一条光谱,244个铁矿石样品共计获得244个LIBS光谱。
1.3 数据处理
1.3.1 VI-BP-ANN
将铁矿石LIBS光谱按照80%和20%的比例随机划分为训练集和测试集,训练集用于训练模型,采用5折交叉验证优化模型参数,测试集用于测试模型的性能。VI-BP-ANN方法流程图如图1所示,包括以下步骤:(1)光谱预处理;(2)使用OOB误差优化RF模型的两个参数,森林中树的数量(ntree)和回归树在节点分支时考虑的特征变量个数(mtry),获得最佳的RF模型;(3)在最优RF模型的条件下,使用RF对铁矿石的LIBS特征进行变量重要性打分,根据变量重要性的高低对特征变量进行重新排序;(4)通过变量重要性阈值对输入到BP-ANN模型的变量数进行控制,使用5折交叉验证均方根误差(RMSECV)和R2优化BP-ANN的神经元个数;(5)选择最佳变量重要性阈值和神经元个数对BP-ANN模型进行训练;(6)输入测试样本的LIBS光谱数据,模型根据变量重要性对特征进行排序,并按照最佳的变量重要性阈值读取光谱特征,返回相关的元素预测结果。

图1 VI-BP-ANN实验方法流程图Fig.1 The flowchart of VI-BP-ANN experimental method
1.3.2 PLS、RF和SVM

1.4 软件运行环境
数据预处理采用Pirouette(Infometrix,Inc),变量重要性测量和反向人工传播神经网络建模均采用Python 3.8.3(Sklearn 0.23.1)自编写脚本完成。实验环境:11th Gen Intel (R) Core (TM) i7-1165G7 CPU@ 2.80 GHz,Intel (R) Iris (R) Xe Graphics GPU,16GB DDR 3200 MHz computer memory。
2 结果与讨论
2.1 LIBS光谱
铁矿石LIBS光谱在180~970 nm波长范围内含有12 814个数据点,其中可以找到Si、Al、Ca、Mg的特征发射线(图2)。铁矿石中Fe的特征发射谱线数量多、强度高,对部分Ca、Mg、Si和Al的特征发射线会产生光谱干扰,如图2 (a)中Ca Ⅱ 373.69 nm受到Fe Ⅰ 373.332 nm的干扰,图2(c)中 Si Ⅰ 390.552 nm受到Fe Ⅰ 390.295 nm的干扰。图2(d)Al Ⅰ 308.215 nm和 Al Ⅰ 309.271 nm特征发射线强度低,容易被噪声掩盖。部分元素特征峰还存在自吸收现象,如图2(b) Mg Ⅰ 517.268 nm。基于铁矿石LIBS光谱基体效应、光谱干扰、自吸收现象的存在,在进行多变量回归分析之前,有必要对原始光谱进行预处理和变量优化。


图2 12种铁矿石的LIBS光谱特征发射线Fig.2 Characteristic emission lines of LIBS spectra of 12 iron ores
2.2 光谱预处理
平滑、多元散射校正(multiplicative scatter correction,MSC)、归一化、归一化+MSC、归一化+平滑5种方法被用于对铁矿石LIBS光谱进行预处理。归一化用来降低脉冲波动和样品的不稳定烧蚀对光谱数据的影响。采用对一定长度窗口的光谱数据点进行K阶多项式拟合进行平滑处理,用来降低噪声的干扰。MSC用于消除不同散射水平带来的光谱差异。不同预处理方法的性能通过5-CV进行优化,采用R2和RMSECV进行评估(图3)。考虑到输入变量对模型的影响,在每一种预处理方法下,对隐藏神经元个数进行了优化,确保模型最优。

图3 基于5-CV不同预处理方法对比Fig.3 Comparison of different pre-processing methods based on 5-CV
与原始光谱相比,在平滑预处理后,SiO2和Al2O3含量的VI-BP-ANN模型性能有所提高[图3(a,b)],而对于CaO和MgO含量的模型有着更差的性能表现[图3(c,d)]。对于MSC的预处理方法,除MgO外,SiO2、Al2O3、CaO含量模型性能都表现更好。而通过归一化预处理方法后,所有模型的性能都得到明显提高。当将平滑、MSC预处理方式分别与归一化结合对光谱进行预处理后,两种组合的预处理方式相比于原始光谱,除CaO含量模型,其余模型性能都出现了提高,而与单一的归一化预处理方法相比,模型的性能均出现了不同程度的降低,R2降低,RMSECV增大;以上分析表明,对于定量分析铁矿石中的SiO2、Al2O3、CaO和MgO,归一化相比于其他预处理方法和原始光谱有着更好的表现性能,此时的RMSECV最小,R2最大,SiO2,Al2O3,CaO和MgO的RMSECV和R2分别为0.861 2 wt%和0.902 7,0.176 3 wt%和0.914 9,0.112 8 wt%和0.942 1,0.274 8 wt%和0.984 1。归一化对模型的性能起主导作用,当在归一化的基础上继续增加平滑、MSC,过多的预处理方式可能会使原始光谱信息失真,从而导致定量精度降低。在实验中将归一化预处理方法用于铁矿石的SiO2、Al2O3、CaO和MgO分析。
2.3 RF参数优化


图4 不同ntree和mtry值与OOB误差的关系(a):SiO2;(b):Al2O3;(c):CaO;(d):MgOFig.4 Relationship between different ntree and mtry values and OOB errors(a):SiO2;(b):Al2O3;(c):CaO;(d):MgO
2.4 变量重要性阈值和神经元优化
为了减少输入BP-ANN模型的变量,根据变量重要性对光谱特征进行了重新排序,通过变量重要性阈值对输入BP-ANN模型的变量进行控制。考虑到输入变量的变化对模型最佳神经元数量的影响。实验充分利用数据集考察模型的性能,通过5-CV对神经元个数(30~50)进行优化,R2和RMSECV作为评价指标。表2—表5分别为SiO2、CaO、MgO和Al2O3的BP-ANN模型在不同变量重要性阈值(变量数)下计算5次的平均结果。

表2 不同变量重要性阈值的BP-ANN模型性能(SiO2)Table 2 Performance of BP-ANN models with different variable importance thresholds (SiO2)
不同变量重要性阈值下的BP-ANN模型性能(SiO2)见表2。当使用原始光谱(12 814)作为输入变量时,此时的最优神经元个数为40,RMSECV平均值为0.042 0 wt%,R2为0.999 7。在变量重要性阈值0~0.001的范围内,随着变量重要性阈值的不断降低,变量数增加,训练集的RMSECV呈现降低的趋势,R2逐渐增加。测试集的RMSEP先增加随后在0.51~0.52 wt%范围内波动,R2先降低之后在0.94~0.95之间波动。时间方面,建模时间随着输入变量数的增多而持续增加,当变量重要性阈值为0.001时,建模时间最短,为3 min 32 s,此时RMSEP最低,模型性能最好。
不同变量重要性阈值下的BP-ANN模型性能(CaO)见表3,随着变量增多,RMSECV逐渐减小,R2不断增大。测试集的RMSEP先降低后增加,阈值为0.000 001时,最佳神经元个数34,此时的模型性能最佳,建模时间较短。
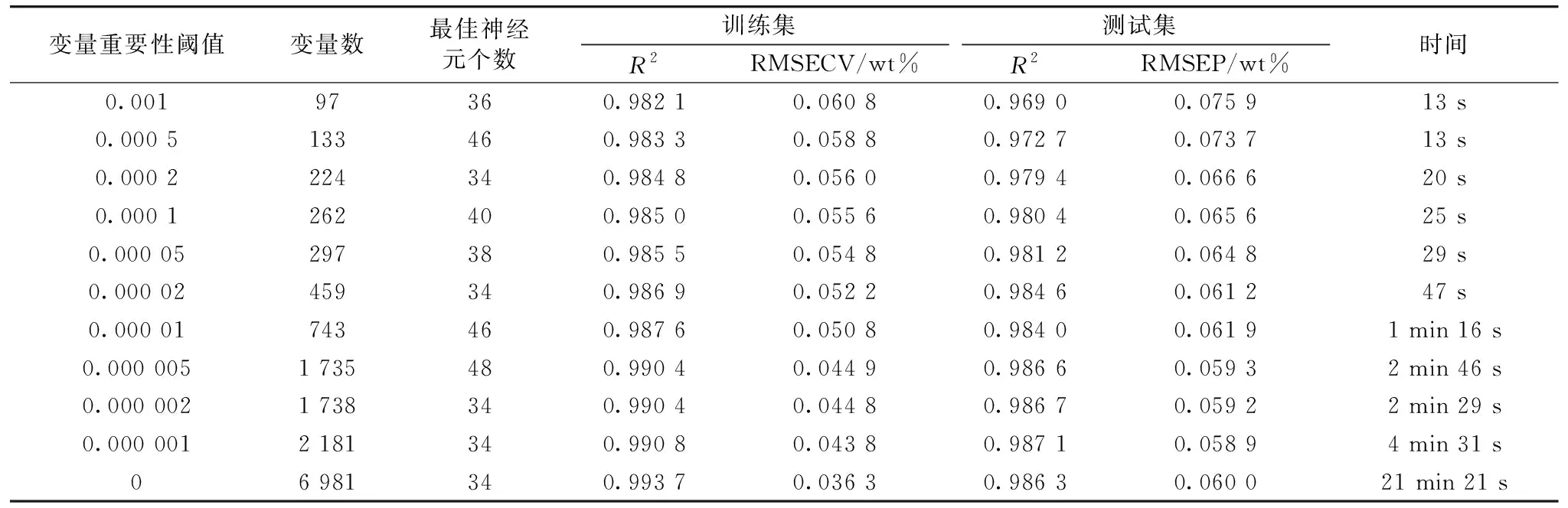
表3 不同变量重要性阈值的BP-ANN模型性能(CaO)Table 3 Performance of BP-ANN models with different variable importance thresholds (CaO)
不同变量重要性阈值下的BP-ANN模型性能(MgO)见表4,随着输入变量的增多,训练集的RMSECV增大,R2减小。而测试集情况与之相反,变量重要性阈值设置为0.001时,最佳神经元个数为38,这时的模型性能最佳,建模时间仅需37 s。

表4 不同变量重要性阈值的BP-ANN模型性能(MgO)Table 4 Performance of BP-ANN models with different variable importance thresholds (MgO)
不同变量重要性阈值下的BP-ANN模型性能(Al2O3)见表5,RMSECV伴随变量数增加持续减小,R2与之相反。测试集中的RMSEP先减小后增大,R2先增大后降低,这可能是由于模型存在过拟合的现象。变量重要性阈值为0.000 2时,最佳神经元个数为44,RMSEP最小,R2最大。

表5 不同变量重要性阈值的BP-ANN模型性能(Al2O3)Table 5 Performance of BP-ANN models with different variable importance thresholds (Al2O3)
2.5 性能测试和对比
采用VI-BP-ANN训练模型对铁矿石测试样本中的SiO2、Al2O3、CaO和MgO含量进行预测,根据RMSEP和R2评价模型的预测能力。结果如图5(a—d)所示,其中MgO的R2高达0.9975,RMSEP为0.141 1 wt%。SiO2的RMSEP为0.377 2 wt%,R2为0.970 1。Al2O3的RMSEP为0.139 9 wt%,R2为0.955 4。CaO的RMSEP为0.058 9 wt%,R2为0.987 1。VI-BP-ANN模型对于铁矿石中的SiO2、Al2O3、CaO和MgO的含量显示出较好的预测能力,测试集的R2均大于0.95。

图5 VI-BP-ANN模型预测结果(a):SiO2;(b):Al2O3;(c):CaO;(d):MgOFig.5 Predicted results of VI-BP-ANN model(a):SiO2;(b):Al2O3;(c):CaO;(d):MgO
使用相同的归一化预处理方法,将VI-BP-ANN方法与PLS、SVM、RF和BP-ANN方法进行了对比。如表6所示为基于5-CV下PLS、SVM、RF、VI-BP-ANN和BP-ANN模型用于分析预测铁矿石中SiO2、Al2O3、CaO和MgO的性能比较。对训练集模型分析,BP-ANN模型性能最佳,VI-BP-ANN模型性能略差,RF性能最差。

表6 基于5-CV模型性能对比Table 6 Model performance comparison based on 5-CV
5种模型在测试集上的预测性能对比如表7所示。对于CaO,RMSEP为0.052 9~0.068 4 wt%,R2为0.977 7~0.987 7。MgO的RMSEP为0.100 2~0.269 7 wt%,R2为0.991 6~0.998 5。对于Al2O3和SiO2,五种模型的RMSEP和R2分别为0.130 7~0.229 4 wt%和0.829 1~0.955 4、0.305 0~0.522 8 wt%和0.942 0~0.970 1。值得注意的是,SiO2模型的RMSEP最大,其次为MgO模型和Al2O3模型,CaO模型的RMSEP最小,结合表1中13种品牌铁矿石的元素组成浓度范围,可能是由于铁矿石样品硅元素含量范围的差异过大所导致。

表7 模型在测试集上的预测性能对比Table 7 Prediction performance comparison of the model on the test set
图6(a—d)为PLS、SVM、RF、VI-BP-ANN和BP-ANN模型用于分析预测铁矿石中硅(以SiO2计)、铝(Al2O3计)、钙(以CaO计)和镁(以MgO计)的性能比较。相比于PLS、SVM、RF和BP-ANN模型,在预测SiO2、Al2O3、CaO和MgO含量时,VI-BP-ANN模型RMSEP值最小,R2值最大,建模时间短,表现出优异的预测能力。

图6 PLS、SVM、RF、VI-BP-ANN和BP-ANN模型的预测性能(a):SiO2;(b):Al2O3;(c):CaO;(d):MgOFig.6 Prediction performance of PLS,SVM,RF,VI-BP-ANN and BP-ANN models(a):SiO2;(b):Al2O3;(c):CaO;(d):MgO
3 结 论
LIBS与VI-BP-ANN相结合成功的应用于铁矿石中硅(以SiO2计)、铝(以Al2O3计)、钙(以CaO计)和镁(以MgO计)含量的定量分析。采用归一化对光谱进行预处理,考虑到输入变量中大量冗余和有害变量对模型的影响,使用RF对LIBS的变量重要性进行了袋外误差的测量,采用变量重要性阈值对输入BP-ANN模型的变量进行控制,最后通过5-CV以RMSECV、R2为评价参数对变量重要性阈值和隐藏层神经元数进行优化。优化的VI-BP-ANN模型用于铁矿石中SiO2、Al2O3、CaO和MgO含量定量分析,并将获得的结果与PLS、SVM、RF和BP-ANN进行对比。结果显示VI-BP-ANN模型在有效降低输入变量的同时整体表现出相对较为优异的预测性能,可实现铁矿石中SiO2、Al2O3、CaO和MgO含量的快速预测。

