基于FLAC3D的双孔隧道围岩稳定性数值模拟分析★

程长清，吴雪琴，赵文广

(1.江苏联合职业技术学院无锡交通分院,江苏 无锡 214151; 2.河南金途科技集团股份有限公司,河南 郑州 450000)

双孔隧道作为现在主要的公路隧道形式,由于其独特的构造以及复杂的受力形式,成为了现在隧道建设者研究的重点与难点,尤其当两个隧道间距较小时,在围岩上覆荷载与支护反力共同作用下就会形成更加复杂的应力场。

目前隧道稳定类的研究方法主要有解析法和数值模拟两大类。对于隧道稳定类问题,有大量学者对此点进行了相关研究。赵明华等[1]基于有限元极限分析双孔隧道的稳定性,得出影响隧道稳定的相关因素。李扬等[2]基于有限元软件Midas对浅埋双孔隧道开挖顺序进行了相关研究。但是他们都是采用有限元软件进行了相关研究工作。也有学者采用有限差分软件[3-8]进行了相关研究,但是他们都是研究单孔隧道或者煤矿等,在开挖及支护后围岩的应力及位移分布。采用有限差分软件FLAC3D进行双孔隧道开挖及支护研究的则相对更少。

因此本文采用有限差分软件FLAC3D对双孔隧道在开挖和支护两种工况下,进行了相关的数值模拟,同时分析了开挖后以及采用锚喷支护后隧道塑性区分布特点,纵向应力场、位移场分布规律。

1 圆形隧道理论模型

关于围岩塑性区发展理论,基于Mohr-Coulomb准则计算的Fenner公式比较经典,但其未考虑中间主应力对于岩石强度的影响。而中间主应力对岩石强度的影响程度为20%～50%[9],显然不考虑中间主应力对于计算结果是有影响的。Drucker-Prager准则计算过程中考虑了中间主应力对于岩石强度的影响,且具有无棱角,易于数学处理的特点,在岩土工程中应用广泛。

1.1 D-P强度准则[10]

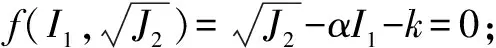
(1)

其中,I1,J2分别为应力张量第一不变量和应力偏张量第二不变量;σ1,σ2,σ3分别为最大主应力,中间主应力和最小主应力;α,k均为与围岩强度参数有关的常数。本文为平面应变问题,α和k的取值见式(2):

(2)

采用中间主应力系数l表示3个主应力之间的关系公式,见式(3):

(3)

由于σ1≥σ2≥σ3,显然有0≤l≤1,将式(3)化简后代入式(1)得式(4),式(5):

I1=(1+l)σ1+(2-l)σ3

(4)

(5)

将式(4),式(5)代入式(1)中,可得由σ1,σ3,l,m,α,k表示的D-P准则表达式(见式(6)):

f=(m-lα-α)σ1-(m-lα+2α)σ3-k=0

(6)

1.2 工程地质情况[11]

工程位置为蓖麻溪隧道K218+120—K218+135,为长期风化剥蚀切割作用形成的山区丘陵地貌。根据物探及工程地质测绘,隧道主要在强风化红砂岩层中,节理裂隙以压扭性为主,且裂隙面闭合,少数呈张性。该隧道为典型的山区高速越岭隧道。隧道埋深100 m,隧道半径为4 m,两个隧道中间拱墙厚度为8 m。假设围岩为理想弹塑性材料,岩土体材料黏聚力c=0.1 MPa,内摩擦角φ=30°,抗拉强度Rt=0.07 MPa,体积模量K=0.33 GPa,剪切模量G=34.48 MPa,重力加速度g=9.8 kg/N,岩体密度ρ=2 200 kg/m3。

1.3 数值计算模型建立

本工程隧道直径8 m,因此取6倍隧道直径为围岩影响范围,又由于本工程属于双孔隧道,于是取计算模型尺寸为72 m×72 m(长×高),为了避免边界效应的影响,取5 m作为工程分析厚度,整个模型包含13 760个计算单元和16 962个网格节点,计算单元长度为1 m。计算时考虑采用Drucker-Prager准则计算其破坏模式。计算过程中固定x=43,x=-29,y=0,y=5,z=-28等位置岩土体的位移,将隧道上覆岩土体的重量换算成面力施加于模型z=8 m面上。本工程采用C25混凝土衬砌进行支护。以水平向右为X轴正向,向内为Y轴正向,向上为Z轴正向。

2 数值计算结果分析

2.1 塑性区

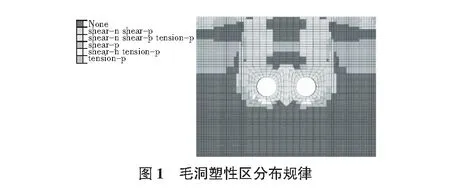
由图1,图2可知,在本工程的地质情况下,施工过程对于原应力场造成较大的影响,施工过程中,隧道开挖造成塑性区的发展,整体趋势表现为:塑性区分布于隧道周围以及上部区域,隧道下部区域塑性区较小,而当施加混喷锚支护后,塑性区明显减小。由锚杆轴力图可知,锚杆所受最大轴力为1.14 MPa,所在区域为两个隧道中间墙上部区域,此处即为施工时需要重点关注部位,该部位应力复杂。另外上部交叉部位锚杆长度至少需要10 m,两个隧道底部位置锚杆需要6 m,其他位置5 m即可穿越塑性区,这也是在设计中需要注意的问题。整体而言双孔隧道需要特别注意隧道顶部与底部位置。

2.2 应力场

2.2.1Z向应力场

未进行支护时,连拱隧道Z向应力场较为复杂,整体表现为:在隧道两侧帮部,应力最大值约为4.2 MPa,而最小值在隧道顶部与底部,最小值约0.2 MPa～0.5 MPa,两者相差38倍,主要原因是开挖引起内部岩土体塑性甚至完全破碎,随着离洞口越来越远,开挖影响则越来越小。

由图3可知,当进行了隧道支护后,隧道周边纵向应力场变的简单,但最大值仍在隧道两侧内壁位置,压应力值最大可达60 MPa左右,相当于未施作锚杆衬砌时的14倍左右,但是塑性区影响面积减小,原因是施加了锚杆与混凝土衬砌后整个体系约束增强,因此受力增大。两隧道中间隔墙应力也由未支护前的0.4 MPa增大为0.6 MPa。

2.2.2X向应力场

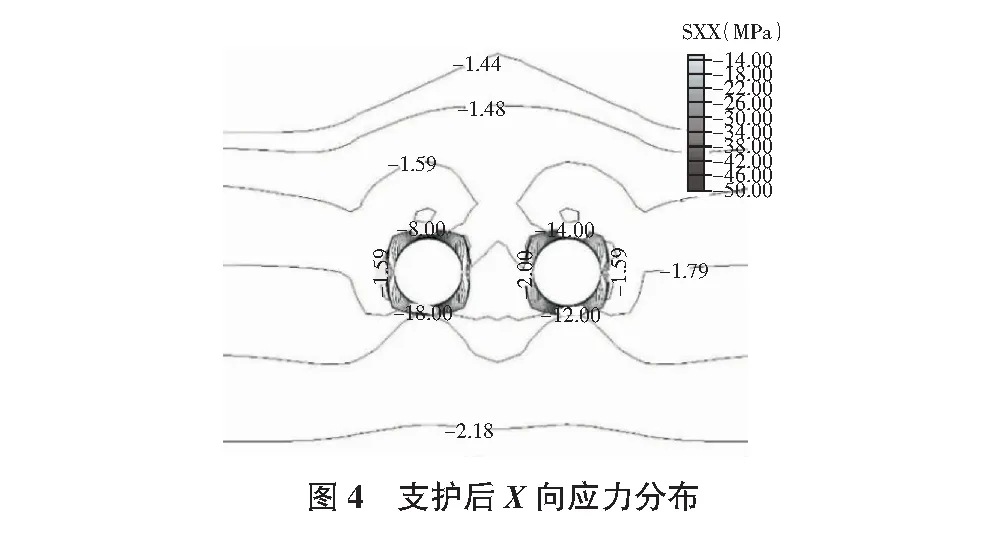
未进行支护时,水平向应力整体值较小,为0.5 MPa～1.5 MPa左右。而由图4可知当施加了锚喷支护后,隧道顶部与底部应力值增大到20 MPa左右。

由图3,图4可知:水平向应力最大值往往出现于隧道的顶部与底部,纵向应力的最大值往往出现于隧道两侧帮部。

2.3 位移场

未进行支护时,隧道Z向位移场也较为复杂,整体表现为:在隧道顶部位移数值较大,最大值为1.8 m,且整体而言两个隧道共同上部区域位移量较大,这也与实际情况相符。而最小值在隧道底部,最小值约0.2 m,可见隧道上部位移量较大有垮塌的危险。

由图5可知,进行支护后,隧道周边纵向位移明显减小(图5中深色区域),但最大值仍然在隧道顶部位置,其值为11 cm左右,隧道底部位移为1 cm～2 cm,分别为未支护时的10%以内,由此可见:支护后隧道位移量大幅度减小,采用锚喷支护具有较好的工程效果。

3 结论

1)工程中采用锚喷支护能有效地减小塑性区的发展,双拱隧道施工过程中的危险位置为隧道顶部与底部。

2)开挖施工后隧道顶部与底部竖向应力相差38倍左右,支护后隧道内整体应力值增大,约为未施作支护的14倍左右。

3)水平向应力最大值往往出现于隧道的顶部与底部,纵向应力的最大值往往出现于隧道两侧帮部。施作了锚喷支护能明显地限制隧道围岩位移的发展。