基于改进GSO算法的变电站蓄电池组监测网络优化方法

安颖坤

（国网湖北省电力有限公司恩施供电公司，湖北 恩施 445000）

0 引 言

随着通信网络技术在电力系统中的广泛应用，各种新型的在线监测方法随之产生。蓄电池在线监测作为一种新型的检测技术，正逐渐被应用于电力系统，可以更好地帮助人们集中了解无人值班变电站的蓄电池工作状况[1-3]。为了保证变电站中蓄电池组的正常有效运行，需要在一定的周期内实现对其各项性能的综合检验和监测。目前，变电站蓄电池组检验与监测的主要手段包括逐个测试单节电池电压与内阻、核容性放电试验等[4]。但是，现有方法在实际应用中存在运行成本高、不利于及时发现蓄电池组异常情况等问题。为促进变电站蓄电池组运行安全性和可靠性的提升，本文将开展基于改进萤火虫群优化（Glowworm Swarm Optimization，GSO）算法的变电站蓄电池组监测网络优化方法设计研究。

1 变电站蓄电池组监测网络节点能耗计算

在对变电站蓄电池组监测网络进行优化前，需要明确变电站蓄电池组监测网络中各个监测节点上的具体能耗情况。针对监测网络中的发送节点，其能耗可以表示为

式中：ETx(b,d)为监测网络中发送节点的能耗；b为发送节点在传输时的数据总量；d为发送节点在传输数据时的距离；εfs为自由空间信道中监测网络的功率放大系数；εmp为多径衰减信道中监测网络运行功率放大系数；Eelec为监测网络发送节点发送或接收单位比特数据时的耗能。在监测网络的发送节点运行过程中，设置一个数据传输距离阈值d0，根据d0与d之间的关系，确定计算发送节点能耗的公式[5]。对于监测网络中接收节点的能耗，计算公式为

式中：ERx(b)为监测网络中接收节点的能耗。从式（2）可以看出，接收节点的能耗不会受到数据传送距离的影响[6]。在对变电站蓄电池组进行监测时，监测网络中的簇头节点需要对相应传感器节点采集到的大量数据进行筛选和融合。这一过程也会产生一定的能耗，用公式表示为

式中：EDA(b)为监测网络中簇头节点筛选、融合数据的过程中产生的能耗；Efuse为完成对每个单位数据融合时监测网络产生的电路损耗量。根据上述论述内容，确定变电站蓄电池组监测网络中各个节点的能耗。

2 蓄电池组监测网络优化目标函数与约束条件设计

在变电站蓄电池组监测过程中，选择网络运行消耗能量最小为优化目标，设计蓄电池组监测网络优化目标函数[7]。在变电站蓄电池组监测网络环境中包含3种不同网络结构，分别为单跳网络、双跳网络以及三跳网络。不同的网络结构对应的能耗不同，主要受到监测范围、感知半径等参数的影响[8]。因此，需要针对不同网络结构分别确定其各自的最小消耗量，其中单跳网络的最小能耗计算公式为

式中：minETol1为单跳网络的最小能耗；ETol-in1为单跳网络发送节点能耗；ETol-CH1为单跳网络接收节点能耗。

双跳网络的最小能耗计算公式为

式中：minETol2为双跳网络的最小能耗；ETol-in2为双跳网络第2个发送节点的能耗；ETol-CH2为双跳网络第2个接收节点的能耗。

三跳网络的最小能耗计算公式为

式中：minETol3为三跳网络的最小能耗；ETol-in3为三跳网络第3个发送节点的能耗；ETol-CH3为三跳网络第3个接收节点的能耗。

在整个监测网络中，存在着上述3种类型网络结构，对应的节点簇分别为单跳节点簇、双跳节点簇以及三跳节点簇[9]。假设3种类型节点簇的数目分别为N1、N2和N3，则能够进一步求解出监测网络中总能耗的最小目标函数，即蓄电池组监测网络优化目标函数为

为确保优化目标函数的合理性，需要结合变电站蓄电池组监测网络实际运行条件及需要，设置相应的优化约束条件。表1中记录了不同指标的约束条件及对应的上限和下限。

表1 不同指标的约束条件及对应的上限和下限

除表1中约束条件以外，对于监测网络中的每个簇节点而言，其数量最少为2，因此还需要设置以下约束条件

式中：ρ为监测网络中传感器节点的分布密度；α为传感器分布扇形圆心角；r为扇形半径；d为到Sink节点的距离。根据上述论述，完成对优化目标函数各个约束条件的设置。

3 基于改进GSO算法的监测网络拓扑结构优化

在明确监测网络的优化目标后，结合改进GSO算法，对监测网络的拓扑结构进行进一步的优化。改进GSO算法是一种随机优化求解算法，主要包括3个组成部分，分别为发现者P、搜索者S以及游荡者R[10]。在寻优的过程中，假设某一成员为i，其在第k次迭代的过程中搜索角度可以用φik表示，搜索方向可以用Dik表示。通过搜索角度的笛卡尔变换，可以进一步推导出搜索方向。若搜索区域围成的结构为三维立体结构，则可以确定发现者P的搜索区域如图1所示。

图1 发现者P的搜索区域

图1中：θ为最大搜索角度；Lmax为最大搜索步长。对于图1中的发现者P，其在搜索区域内进行更新的公式为

式中：X为更新位置；Xpk为发现者P在第k次迭代过程中的所在位置；r1为服从标准正态分布的随机数；为发现者P的搜索方向；φk为在第k次迭代时的搜索角度。根据式（9）对搜索区域进行更新，直到发现者P找到最优解为止，完成迭代，并利用最后一次搜索结果确定监测网络的拓扑结构。

4 对比实验

为了进一步验证该方法的实际应用可行性及有效性，选择将应用本文优化方法后的监测网络作为实验组，将利用本文优化方法优化前的监测网络作为对照组。选用一组52节48 V 500 Ah型号蓄电池组作为此次实验的研究对象。该蓄电池组的额定容量为500 Ah，运行电压为48 V，转化效率为0.99，外形尺寸为997 mm×670 mm×380 mm。选择利用2种监测网络监测到的相关参数，对变电站蓄电池组剩余电量进行测定。蓄电池组剩余电量可以表示为

式中：SSoC为蓄电池组剩余电量占相同条件下额定容量的百分比；Qc为通过监测网络监测到的蓄电池组的剩余容量；QI为恒定电流放电过程中通过监测网络监测到的蓄电池容量。分别利用优化前后的监测网络对相同时刻的变电站蓄电池组剩余电量的相关数据进行监测，并利用式（10）计算得出蓄电池组剩余电量占相同条件下额定容量的百分比。SSoC的取值范围为0～1，当取值为0时，说明此时蓄电池组已经完全放电；当取值为1时，说明此时蓄电池组处于完全充电状态。将2组监测网络得到的结果与该变电站蓄电池组在对应时刻的实际剩余电量和充放电状态进行对比，得到如表2所示的实验结果。

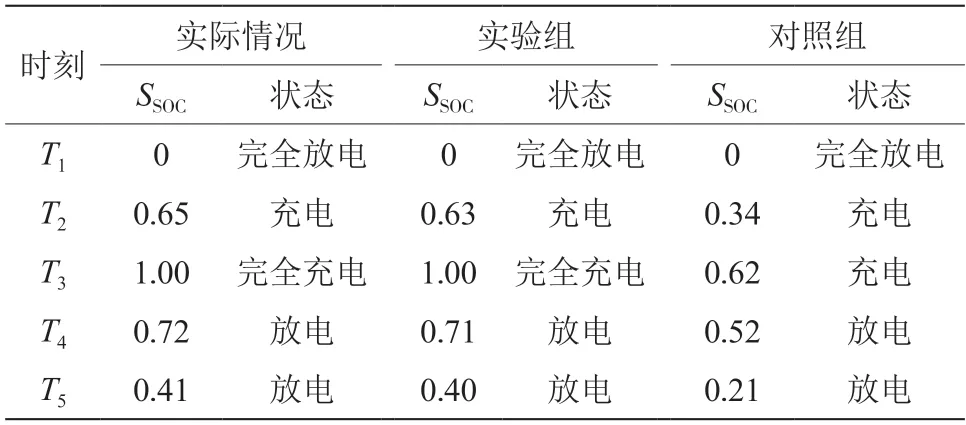
表2 监测网络优化前后监测效果对比表

结合表2中记录的监测网络优化前后的监测结果可以看出，实验组的监测网络获取到的监测数据SSoC结果更接近实际，差值最大不超过0.01；而对照组的监测网络获取到的监测数据SSoC结果与实际相差较大，差值超过了0.20。因此，通过实验可以证明，应用提出的优化方法对监测网络进行监测可以有效提高对变电站蓄电池组的监测精度，即优化方法具备应用可行性和有效性。

分别针对优化前后监测网络中的单跳网络、双跳网络以及三跳网络运行能耗进行记录，并结合相关公式得到监测网络整体能耗。为方便比较，记录得到的数据结果如表3所示。

表3 监测网络优化前后运行能耗对比

对表3中实验数据分析得出，实验组利用优化方法优化后的监测网络在运行过程中的整体运行能耗仅为3.73×10-4J，而未应用优化方法优化的对照组监测网络的整体运行能耗达到了8.03×10-4J。由此可以清晰看出，提出的优化方法在应用后可以有效降低变电站蓄电池组监测网络的运行能耗，促进监测网络整体运行性能的提升。

5 结 论

基于改进GSO算法，设计了一种全新的针对变电站蓄电池组监测网络的优化方法，并通过对比实验的方式验证了该优化方法的应用可行性。利用提出的优化方法对监测网络进行监测，可以在极大程度上提高监测精度，确保监测网络始终保持较低的能耗运行，提升网络的运行性能。