飞艇附加质量的水动力模型试验技术研究
史圣哲, 高现娇, 左仔滨, 焦俊
(1.中国特种飞行器研究所, 荆门 448035; 2.高速水动力航空科学技术重点实验室, 荆门 448035)
飞艇的动导数和附加质量分别表征其在有黏流和无旋无环流中所受非定常气动力/力矩[1],附加质量效应使飞艇的操纵响应变得缓慢[2],通常可以采用风洞中动导数试验技术获得飞艇的附加质量。风洞中动导数试验技术按照试验模型有无外界强迫驱动力矩,可分为自由振动和强迫振动两种试验方法[3],张永升[4]、Shi等[5]和陈昊等[6]采用强迫振动试验方法获得航天飞行器、X型尾翼飞艇、某翼身融合布局模型在俯仰、横滚、偏航方向的动导数(附加质量)。刘金等[7]和赵俊波等[8]则通过自由振动方式获得动导数(附加质量)。动导数试验技术不能满足飞艇附加质量测量的要求,主要体现在以下几个方面:在此动导数试验方法中,动导数试验方法只能提供俯仰、横滚及偏航3个方向的运动,即三方向姿态角度为0°的动导数试验,只可以求得3个转动方向的附加质量,缺少了3个平动方向的附加质量。飞艇附加质量的流体介质是空气,其受力和力矩测量值很小,天平反应不明显[9]。
现通过开展飞艇附加质量的水动力模型试验技术研究,将标准椭球体模型、飞艇水动力模型在水中强迫正弦周期性往复运动得到的力和力矩与在空气中强迫正弦周期性往复运动得到的力和力矩,对应相减,求得其与运动的同相分量,依据公式,换算得到相应的飞艇附加质量。飞艇附加质量的水动模型试验技术可以逐次获得6个方向的附加质量,相比风洞附加质量试验技术,拓展3个平动方向的附加质量测量范围;且在水池中测量的力和力矩是风洞中测量的力和力矩的800倍,有效地克服天平传感器测量误差的影响。
1 试验原理
飞艇附加质量的水动模型试验是基于小振幅强迫振动动导数试验原理。
通过在水中和空气中分别进行各个运动方向上的强迫正弦周期性往复运动,得到水中和空气中各个运动方向上的力时历和力矩时历;将水中的时历力和力矩,与空气中的时历力和力矩,对应相减,求得飞艇水动模型各个方向上力和力矩关于运动的同相分量和正交分量,依据公式,换算得到各个方向上力和力矩的线速度导数、角速度导数、线加速度导数和角加速度导数;对飞艇水动模型的各个方向上力和力矩的线加速度导数或角加速度导数取反,获得飞艇水动模型各个方向上的附加质量;依据相似准则,换算得到飞艇实艇的附加质量矩阵。
2 飞艇附加质量水动试验技术
飞艇附加质量水动试验技术是在水池通过对飞艇水动力模型进行六自由度方向上强迫正弦周期往复运动试验,测量飞艇水动力模型的附加质量,并换算为实艇的附加质量。
2.1 试验装置
在进行飞艇附加质量水动试验时,要求附加质量模型在6个自由度方向上进行周期性往复运动。采取如图1所示试验装置,自上至下,分别为六自由度运动平台、连接杆、水密天平、附加质量模型。附加质量模型的型心,即飞艇三维坐标原点,位于水下1 m处。通过六自由度运动平台实现飞艇附加质量模型在6个方向上的强迫正弦运动。图2在水中的飞艇附加质量试验。
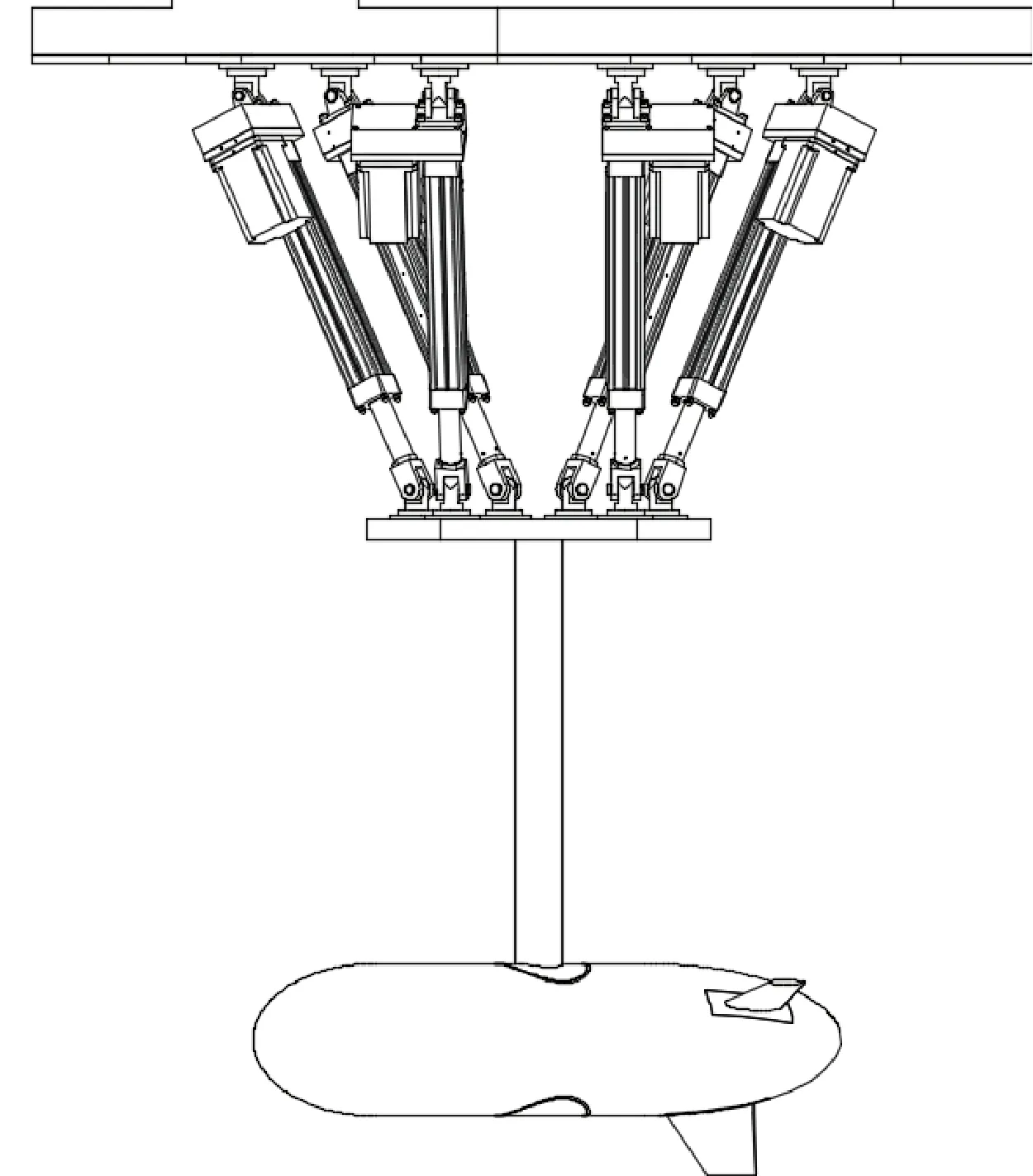
图1 飞艇附加质量试验装置

图2 在水中的飞艇附加质量试验
2.2 试验模型的安装
在进行试验前需要将连接杆与六自由度运动平台、水密天平进行安装,试验模型中轴线距水面距离大于0.5倍的艇长,在正式试验前,需进行试运行,确保飞艇水动力模型是延各方向的轴线进行线性周期往复运动或旋转周期往复运动。
2.3 试验状态
试验前先要选择试验状态参数,包括模型运动方向、模型运动类型、模型运动幅值、模型运动周期。模型运动方向包括X、Y、Z轴运动;模型运动类型包括平动正弦周期性往复运动、转动正弦周期性往复运动;模型运动幅值、模型运动圆频率需由试验任务书或试验大纲给出,确保飞艇水动力模型在运动过程中的受力和力矩小于水密天平的量程。试验分别进行两个阶段,分别为在空气中的飞艇附加质量模型六自由度方向强迫正弦周期往复运动和在水中的飞艇附加质量模型六自由度方向强迫正弦周期往复运动。
3 试验数据处理
在试验过程中,由于动力系统电机工作过程中的高频振动和线圈转动产生的磁场影响,传感器采集的信号带有一定的干扰。试验数据处理需对所采集数据进行相应的预处理,飞艇附加质量水动试验的理想采集信号为低频信号,处理时利用低通滤波器以运动频率的1.5倍作为滤波频率将试验信号中高频信号滤除,然后取比较稳定的数据进行分析。对受力和力矩的时历曲线进行正弦拟合,给出幅值和相位差。
3.1 纯横荡运动的数据处理
平动类运动以纯横荡为例,将飞艇纯横荡运动时受到的时历力和力矩,分解为与横荡同相位的流体惯性力(力矩)、与升沉相位正交的阻尼力(力矩)、常量部分。则可得

(1)
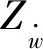
3.2 纯艏摇运动的数据处理
转动类运动以纯艏摇为例,将飞艇纯艏摇运动时受到的时历力和力矩,分解为与艏摇同相位的流体惯性力(力矩)、与艏摇相位正交的阻尼力(力矩)、常量部分。则可得
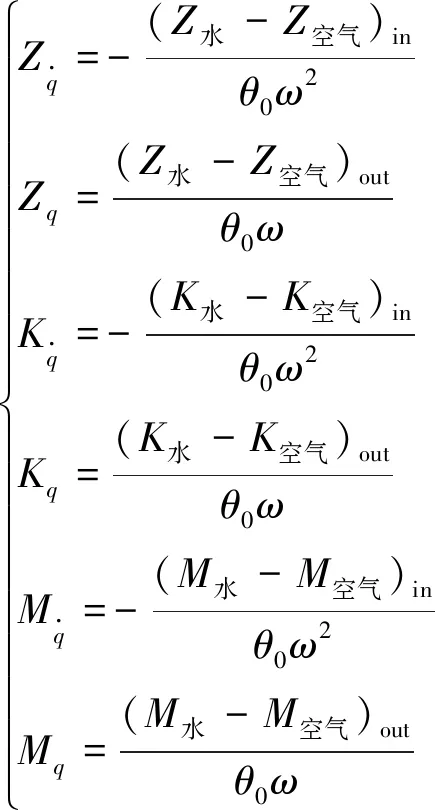
(2)

3.3 其他平面运动的数据处理
4 试验步骤
(1)模型的安装。参照图1,自上至下依次安装六自由度运动平台、连接杆、水密天平、飞艇水动力模型。需保证飞艇水动力模型是水密的,水密天平坐标原点、方向与飞艇水动力模型坐标原点、方向是一一对应重合的。
(2)空气中强迫正弦周期性往复运动。通过控制六自由度运动平台,以特定的圆频率和幅度,实现飞艇水动力模型在6个方向上的强迫正弦周期性往复运动,得到相应的力和力矩的时历曲线。
(3)水中强迫正弦周期性往复运动。在水中重复在飞艇水动力模型强迫正弦周期性往复运动的圆频率、幅值,与空气中强迫正弦周期性往复运动的圆频率、幅值保持一致,得到相应的力和力矩的时历曲线。
(4)试验数据的处理。将水中强迫正弦周期性往复运动得到的力和力矩与将空气中强迫正弦周期性往复运动得到的力和力矩,对应相减,求得其与运动的同相分量,依据公式,可以换算得到相应的飞艇附加质量。
5 飞艇附加质量试验结果
5.1 标准椭球体的附加质量试验结果
如图3所示,待验证的椭球体(2a=20 m,2b=5.333 m,ρ=1.225 kg/m3)可以作为一个标准模型,通过数值仿真[10-12]或势流理论[13]的方式计算其附加质量。标准椭球体的水动力模型为1∶10缩尺比的钢骨架玻璃钢壳体模型,水动力模型的长度为2 m。标准椭球体的水动力模型重量约为其排水质量的一半,即标准椭球体的水动力模型在空气中和水中的向下的力和向上的力较为接近,占用水密天平向上或向下的量程基本相等。

图3 标准椭球体的水动力模型
以标准椭球体的水动力模型在水中纯垂荡运动试验为例,六自由度运动平台施加在标准椭球体水动力模型上特定垂向的强迫正弦周期性往复运动。在全部20个周期中,前2个周期运动幅值由0逐渐增加到指定幅值,后2个周期运动幅值由指定幅值降低到0,这样可以避免突然启动或停止对六自由度运动平台造成损坏。图4为标准椭球体在水中纯垂荡运动的试验曲线,黑色实线为垂荡位移随时间变化曲线,运动幅值为50 mm,运动频率为1.25 Hz,蓝色实线为水密天平测得的垂向力随时间变化曲线。通过滤波、拟合、去平衡均值等步骤,可以获得稳定时间段的垂荡位移、垂向力的正弦公式的表达形式,即幅值、圆频率、初始相位,6个方向附加质量试验结果如表1所示。

表1 标准椭球体的水动力模型试验结果
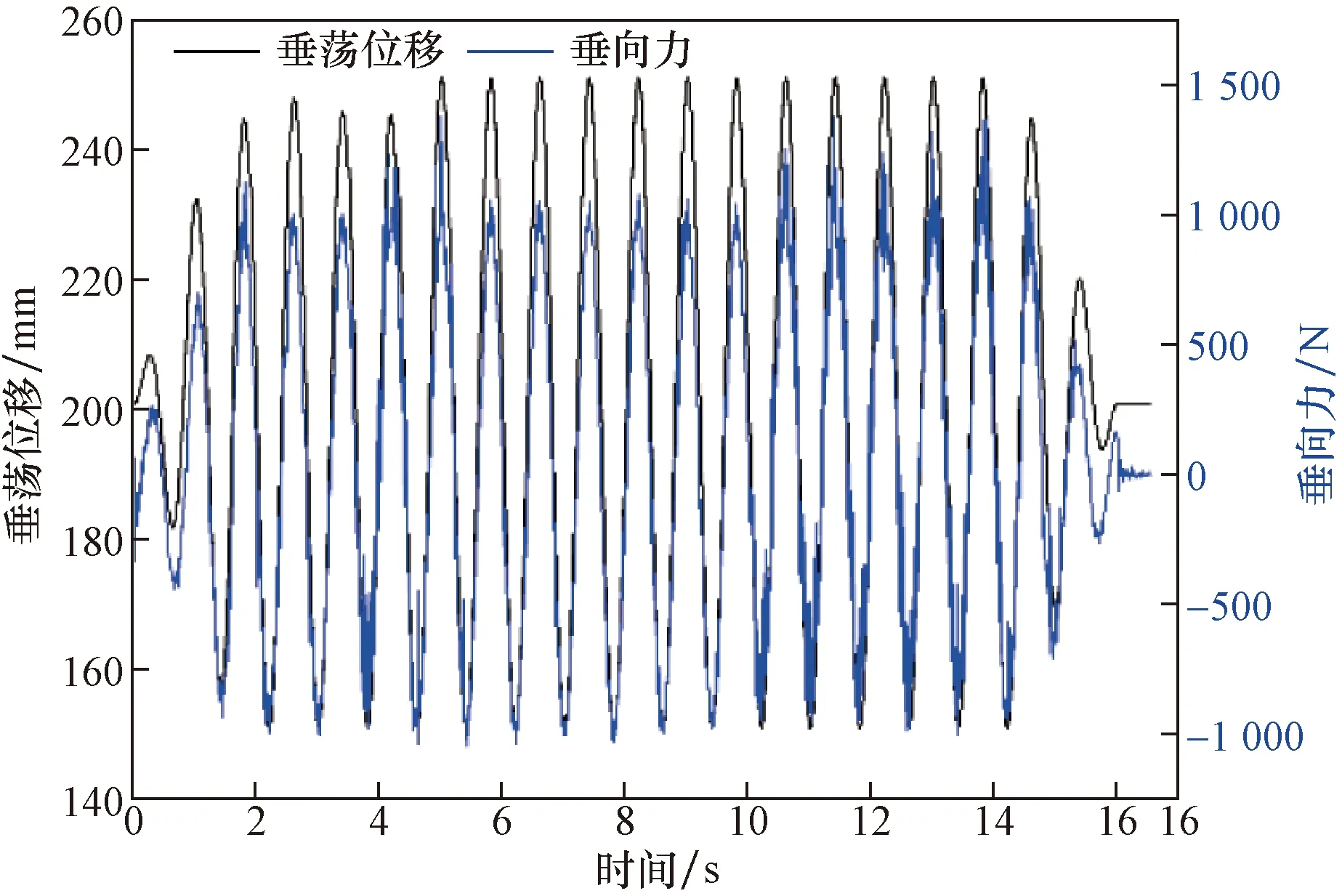
图4 标准椭球体在水中纯垂荡运动的试验曲线
表1中所有工况均需要重复10次,通过取多次试验值的平均值,来降低试验误差。将水中和空气中测得的质量或惯量对应相减,即为该方向的附加质量。对于纯纵荡运动、纯垂荡运动、纯横荡运动方向的附加质量,模型试验值与实际值呈缩尺比的三次方关系;对于纯横滚运动、纯艏摇运动、纯俯仰运动方向的附加质量,模型试验值与实际值呈缩尺比的五次方关系;并将水的密度换算为空气的密度,即可得到实尺寸标准椭球体的附加质量的水动试验值。
根据标准椭球体(缩尺比1∶10)附加质量λij水动试验值(10次试验结果平均值)与理论值可进行误差分析,结果如表2所示。
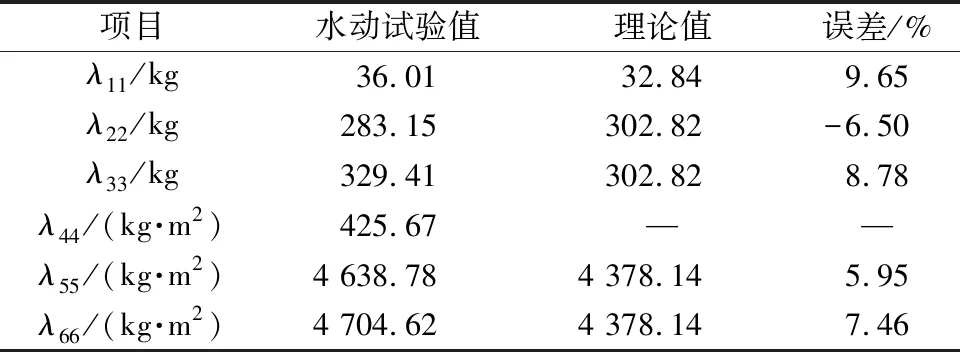
表2 标准椭球体主方向上的附加质量误差表
根据表2可知,标准附加质量在纵荡、垂荡、横荡、艏摇、俯仰方向上的附加质量误差分别为9.65%、-6.50%、8.78%、5.95%、7.46%。经过标准椭球体验证的飞艇附加质量的水动力模型试验技术,其试验误差小于10%,可以用于目标飞艇附加质量的水动试验。
5.2 飞艇的附加质量试验结果
目标飞艇为中段大尺寸等值面圆柱单囊体、倒Y形尾翼布局形式。根据目标飞艇(缩尺比1∶100)附加质量水动试验值与数值计算值可进行误差分析,结果如表3所示。
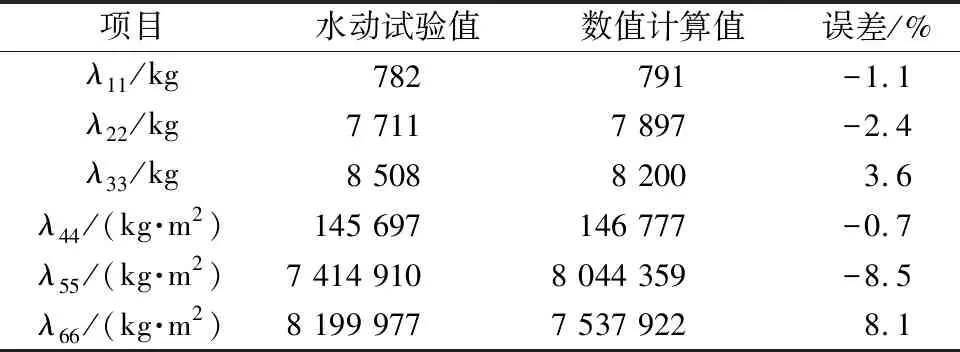
表3 飞艇主方向上的附加质量误差表
根据表3可知,飞艇附加质量在纵荡、垂荡、横荡、横滚、艏摇、俯仰方向上的附加质量误差分别为-1.1%、-2.4%、3.6%、-0.7%、-8.5%、8.1%。
6 结论
(1)飞艇附加质量的水动力模型试验技术通过缩比模型水动试验,逐次测试6个方向惯性力和力矩的大小,依据公式,通过换算求得飞艇附加质量,不需要二次安装和调试。相比风洞附加质量试验技术,拓展了3个平动方向的附加质量测量范围。
(2)标准椭球体在纵荡、垂荡、横荡、艏摇、俯仰方向上的附加质量误差分别为9.65%、-6.50%、8.78%、5.95%、7.46%,标准椭球体主方向上的附加质量均不大于理论值的10%,表明了飞艇附加质量的水动力模型试验技术是有效的,可以替代并补充风洞附加质量试验技术。
(3)飞艇附加质量在纵荡、垂荡、横荡、横滚、艏摇、俯仰方向上的附加质量误差分别为-1.1%、-2.4%、3.6%、-0.7%、-8.5%、8.1%。

