进场航空器跑道占用时间预测

李楠, 傅饶

(中国民航大学民航航班广域监视与安全管控技术重点实验室, 天津 300300)

跑道吞吐量对于空域资源的利用至关重要。由于大型机场的跑道容量有限,经常出现空域资源紧张、协调及运行保障压力大的现象[1]。跑道占用时间的预测可以提高跑道使用效率,为管制员提供高效、准确的决策信息,实现航空器行为及时、合理的调整,从而保航空器运行的安全性。在此驱动下,准确的预测进场航空器的跑道占用时间,计算进场航空器之间合理的时间间隔,是进场管理系统(arrival management,AMAN)和机场协同决策系统(airport collaborative decision making system,ACDM)中有效利用进场时隙的重要前提。同时可以为机场运行效率的研究提供理论参考。

国外学者对于跑道占用时间的预测展开了广泛的研究。Spencer等[2]基于贝叶斯算法对美国27个机场的进、离场航空器跑道占用时间及滑行距离进行预测,提出了不同航空器降落和起飞性能中存在巨大差异;Meijers等[3]运用数据驱动的方法来探究跑道占用时间的影响因素,并重点研究了不同因素对跑道占用时间预测的影响;Meijers等[4]使用递归神经网络模型预测每个可用跑道出口的使用概率和航空器使用该出口离开跑道时的跑道占用时间(runway occupancy time, ROT),并使用该模型确定可以最大降低ROT的跑道出口位置;Nguyen等[5]运用决策树、随机森林和梯度提升模型3种方法对跑道占用时间预测结果进行对比研究; Mirmohammadsadeghi等[6]通过蒙特卡洛方法对每架飞机着陆的关键参数进行仿真,并采用了数据驱动方法建立预测模型;Stempfel等[7]根据苏黎世机场收集的3年数据,基于梯度增强回归模型,对跑道占用时间预测的准确率进行分析,以此增加跑道容量;Friso等[8]结合神经网络、多层感知器(multilayer perceptron,MLP)、Lasso和回归树模型,建立了进场航空器跑道占用时间 (arrival runway occupancy time,AROT)的预测模型,并使用戴高乐机场和维也纳机场的数据预测了异常的跑道占用时间。

国内研究主要通过将跑道占用时间预测与跑道占用时间间隔相结合进行研究,而针对跑道占用时间的单独研究则较少。张定鹏[9]结合单跑道运行方式中航空器跑道占用时间间隔规定的特点,构建配对进近模式下航空器跑道占用时间间隔模型;金京等[10]采用函数拟合的方法,在特定气象条件下对跑道占用时间进行预测并由此推定起飞间隔标准;张兆宁等[11]建立航空器脱离跑道时间优化模型,得到航空器脱离跑道的最短时间和到达跑道穿越点的最早时刻,并进一步建立航空器滑行路径优化模型,提高跑道使用效率;刘涛[12]利用前馈型神经网络模型对跑道占用时间进行预测,基于跑道占用时间构建跑道容量模型,模拟评估不同飞机类型到达组合的跑道容量。

在上述研究中,没有考虑跑道入口端速度、跑道出口端速度对跑道占用时间的影响,导致预测精度降低。因此,现增加跑道入口端速度和跑道出口端速度的分析,分析这些因素的作用,并使用改进的GWO-RF方法预测跑道占用时间,得到一个最佳的跑道占用时间预测模型。

1 数据描述

1.1 样本数据分析

对2020年12月美国纽瓦克自由国际机场的进离场航班进行了统计分析,时间为30 d,涵盖了12月的所有工作日及节假日。这些数据的总数为343 110条,原始数据信息包括时间戳、航班号、机型、经度、纬度、高度、地速和航向。航空器样本数据集如表1所示。

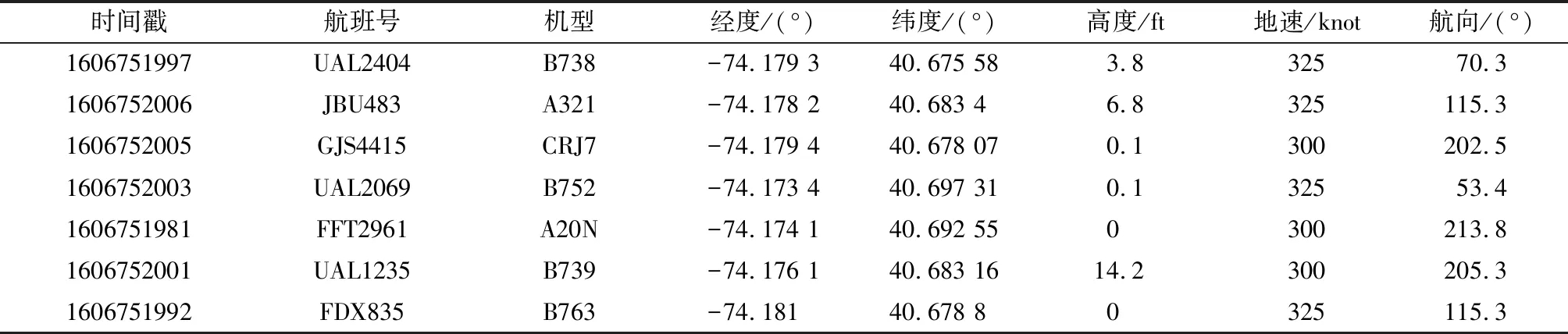
表1 原始数据

1.2 跑道占用时间的定义与提取

美国联邦航空管理局[13]将跑道占用时间定义为:航空器从跑道入口到脱离跑道所用时间;欧洲航空安全组织[14]将跑道占用时间定义为:航空器接地点到脱离跑道所用时间; 中国民用航空局[15]将跑道占用时间定义为:航空器占用跑道,包括航空器起飞和着陆占用地面保护区的总时间。本文研究采用的数据是美国纽瓦克自由国际机场的数据,为了更加符合实际运行,现采用美国联邦航空管理局对跑道占用时间的定义。计算公式为

ROT=tend-t0

(1)

式(1)中:ROT为进场航空器跑道占用时间;t0为航空器飞至跑道入口端的时刻;tend为航空器落地后滑行脱离跑道的时刻。

首先,进行数据整理。基于航空器编码,识别出第一组独立的飞行轨迹。然后通过识别此组飞行轨迹中时间间隔超过10 min的连续数据点,创建新的精细飞行轨迹。使得具有相同航空器编码的航班能够被分开,飞行轨迹被细分。

其次,运用数据识别将进场航空器的飞行轨迹与离场航空器的轨迹分离。通过反复实验,选择出两个合适的阈值将轨迹可视化。本文研究选择的阈值为当航空器到达跑道入口端的速度大于100 kt、航空器脱离跑道时的速度低于20 kt时,此飞行航迹被识别为着陆飞行。

再次,对识别出的进场航空器轨迹以每秒为单位进行线性插值,补全航空器每秒的经度坐标、纬度坐标、速度、航向和高度信息。

最后,根据跑道占用时间的定义,提取两个时间戳来计算跑道占用时间。这两个时间戳分别对应于航空器飞越跑道入口端的时间和其尾部脱离跑道的时间。第一个时间戳t0的提取根据飞行轨迹插值后到达跑道入口端的最近点确定,第二个时间戳tend的提取根据航空器脱离跑道后距离跑道的最小垂直距离确定。因为记录航空器位置的GPS天线通常位于航空器的中心附近,因此当航空器的中心距离跑道边界的垂直距离D大于航空器垂直于跑道轴上的投影长度一半时,航空器被认定为脱离跑道。可使用式(2)计算垂直距离D,计算示意图如图1所示。

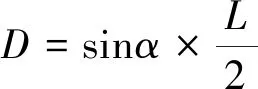
(2)

式(2)中:α为跑道出口的角度;L为飞机的总长度;D为提取出的航空器离开跑道后距离跑道边界的最小垂直距离。

此时对应的轨迹点被识别,tend被提取。最后通过计算tend和t0之间的差值来计算跑道占用时间。跑道占用时间小于20 s的值通常对应于质量较差的飞行轨迹,其位置、速度和高度值不可靠,因此被忽略。总共从343 110条轨迹中提取出2 069架次进场航班的跑道占用时间测量值。

对获取的数据进行去噪声处理后得到样本总体最大值、最小值、平均值、中位数和标准差,如表2所示。表2中的第25百分位数及第75百分位数表明,纽瓦克机场进场航空器的跑道占用时间集中在44～63 s。

表2 航空器跑道占用时间统计分析

图2为纽瓦克机场进场航空器跑道占用时间频率分布。由图2可知,纽瓦克机场进场航空器跑道占用时间呈现右偏态分布,其偏度和峰度分别位3.16、0.90。通过表2和图2可知,提取出的跑道占用时间准确性较高,符合美国联邦航空管理局的规定和实际运行情况。

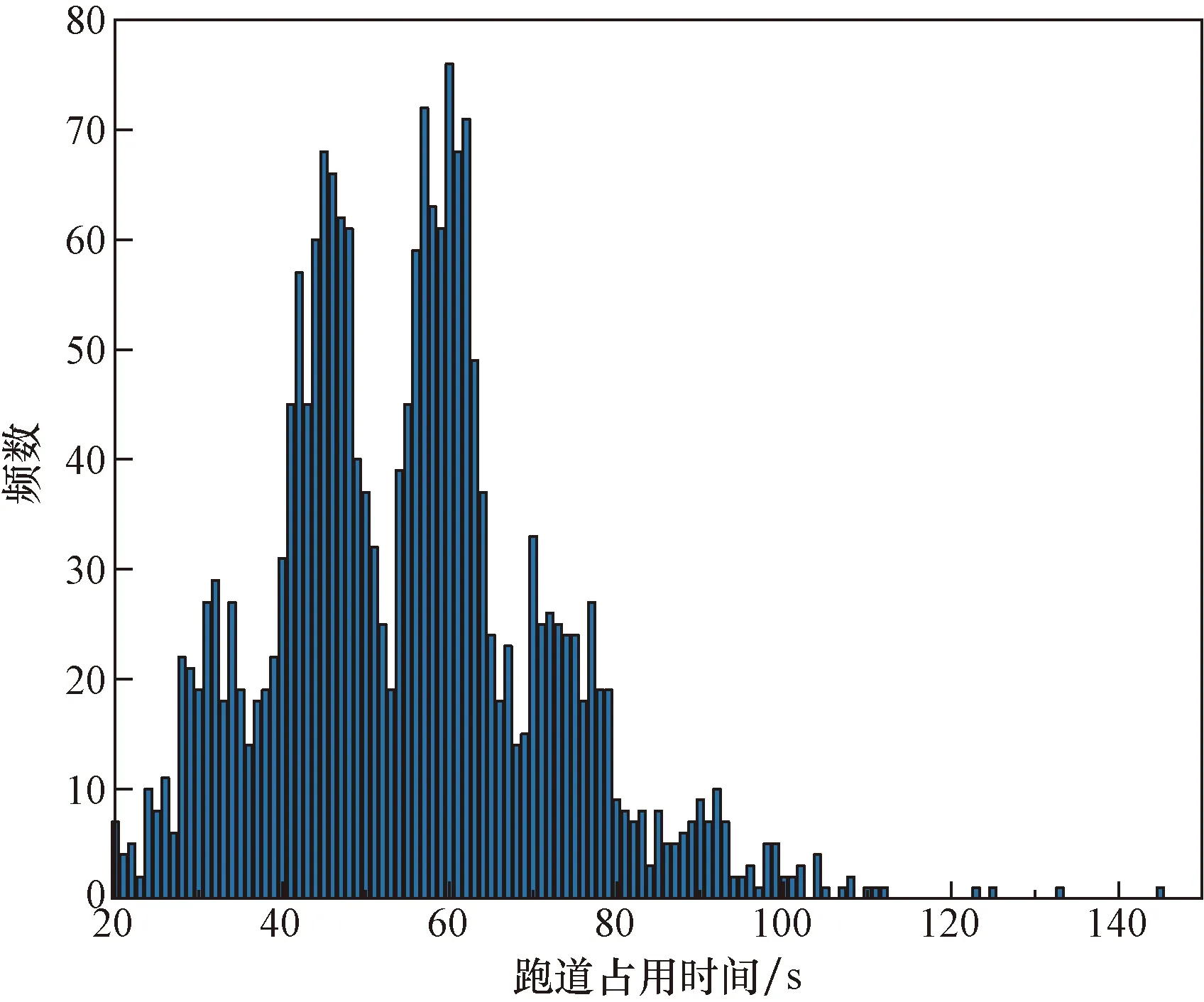
图2 纽瓦克机场进场航空器跑道占用时间分布

1.3 影响跑道占用时间的关键指标定义与分析

1.3.1 机型性能

图3显示了每个尾流类别(一般中型、超中型、一般重型和超重型)航空器ROT的累积分布。由图3可知,不同尾流类别的航空器跑道占用时间分布不同,并且属于最大起飞重量(maximum takeoff weigh,MTOW)较高类别的航空器平均跑道占用时间较高。

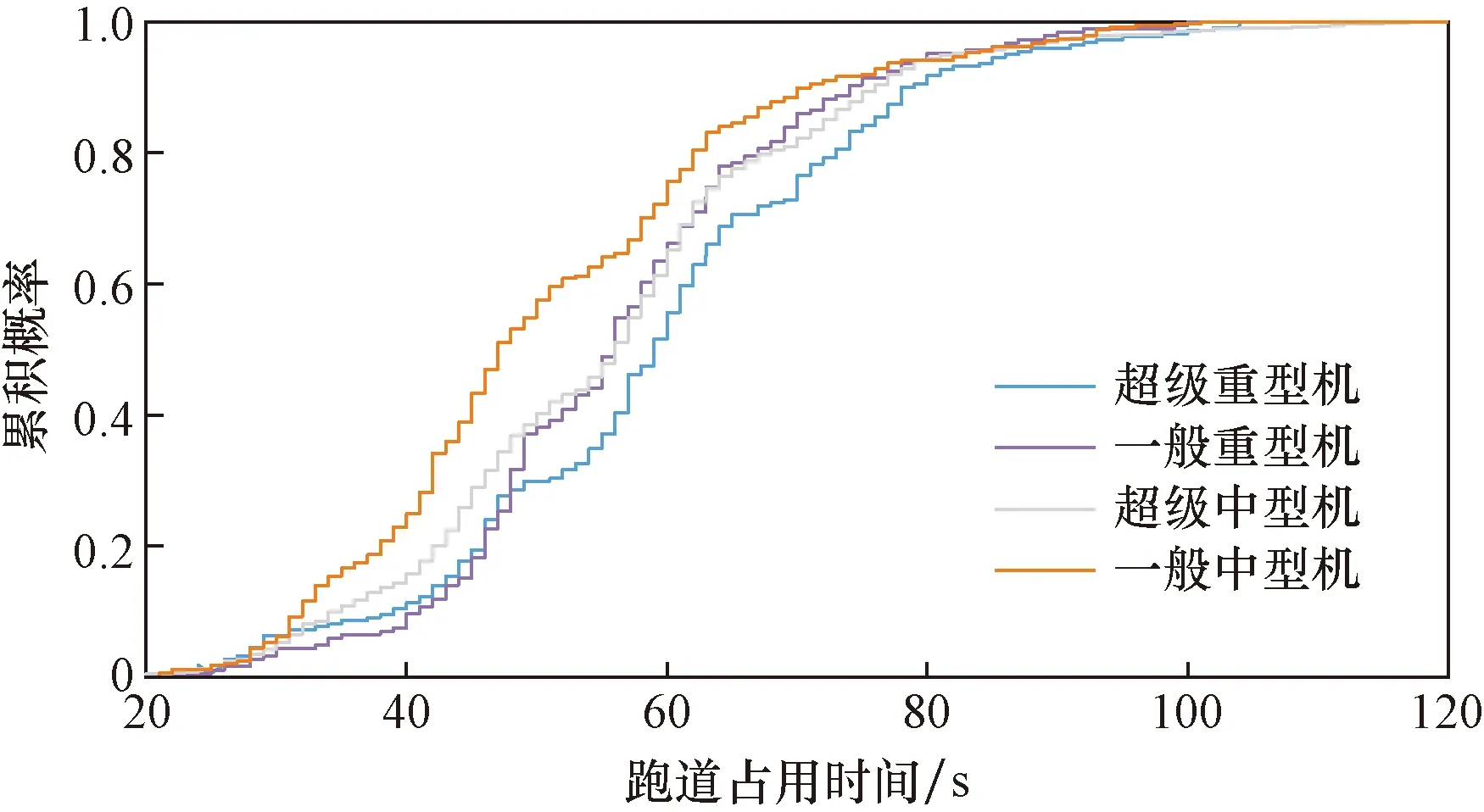
图3 不同尾流类别的ROT累积分布

即使在每个尾流类别中,不同的航空器也具有不同的ROT分布。大型飞机不仅具有较大的最大起飞重量,而且因为其尾流间隔的要求具有较高的进近速度,这些因素均导致航空器的动量增大,从而得到较高的ROT。如图4所示,图4显示了属于“中型”类别的4种常见航空器的ROT累积分布。在B737和A320系列中,最大机型(B738和A321)的跑道占用时间更高。

图4 4种常见“中型”航空器的ROT累积分布

由于ROT与飞机类型的依赖性,可以通过查看特定的飞机类型来分析其他因素对ROT的影响。因此对影响因素的研究均采用A320飞机进行重点分析。

1.3.2 航空公司

由于不同的航空公司拥有不同的机队,并且不同航空公司工作的飞行员接受不同的飞行员培训,遵循不同的操作程序,如使用不同的自动刹车设置等。因此,飞行员驾驶航空器着陆的方式有所不同。图5为美国3家广泛使用A320航空器航空公司的ROT分布。从图5可知ROT分布有明显差异。

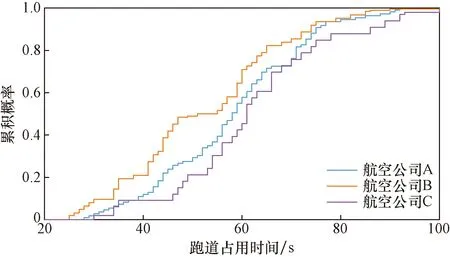
图5 不同航空公司的A320 ROT累积分布

1.3.3 跑道出口选择与跑道出口角度

跑道的关键参数包括跑道出口距跑道入口端的距离以及跑道出口与跑道轴线的夹角。其中跑道出口角度是滑行道中心线与跑道中心线组成的夹角,夹角范围为0°～180°。如图6所示,最常用的出口角度为90°(即直角出口)和30°(即快速脱离出口)。航空器在进入跑道出口安全转弯时,需要降低速度,随着出口角度的增大,速度降低率需增加。因而与直角出口相比,快速脱离道口可以使航空器以更高的速度离开跑道,减少跑道上的制动距离,降低跑道占用时间并增加跑道容量。图7显示了高速30°出口和60°出口之间的ROT累积分布差异。基于这一逻辑,在影响跑道占用时间的因素时引入跑道出口角度这一变量。

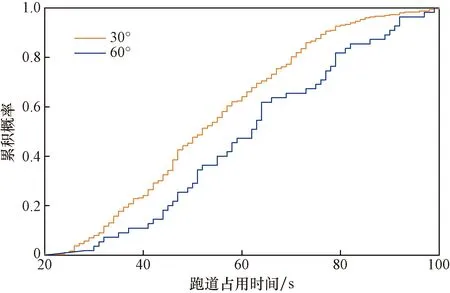
图7 不同出口角度的ROT累积分布

跑道出口的选择影响航空器从跑道入口沿跑道中心线到开始转弯从特定跑道出口滑出的直线距离。这个距离是航空器着陆前大幅度减速的距离,一般来说,跑道出口位置离跑道入口端距离越短跑道占用时间越短。如图8所示,ROT随着跑道出口距跑道入口距离的增加而增加,增加约0.24 s/m。因此航空器每次着陆选择的出口位置将对跑道占用时间产生很大影响,需要在跑道占用时间模型中引入跑道出口的选择。

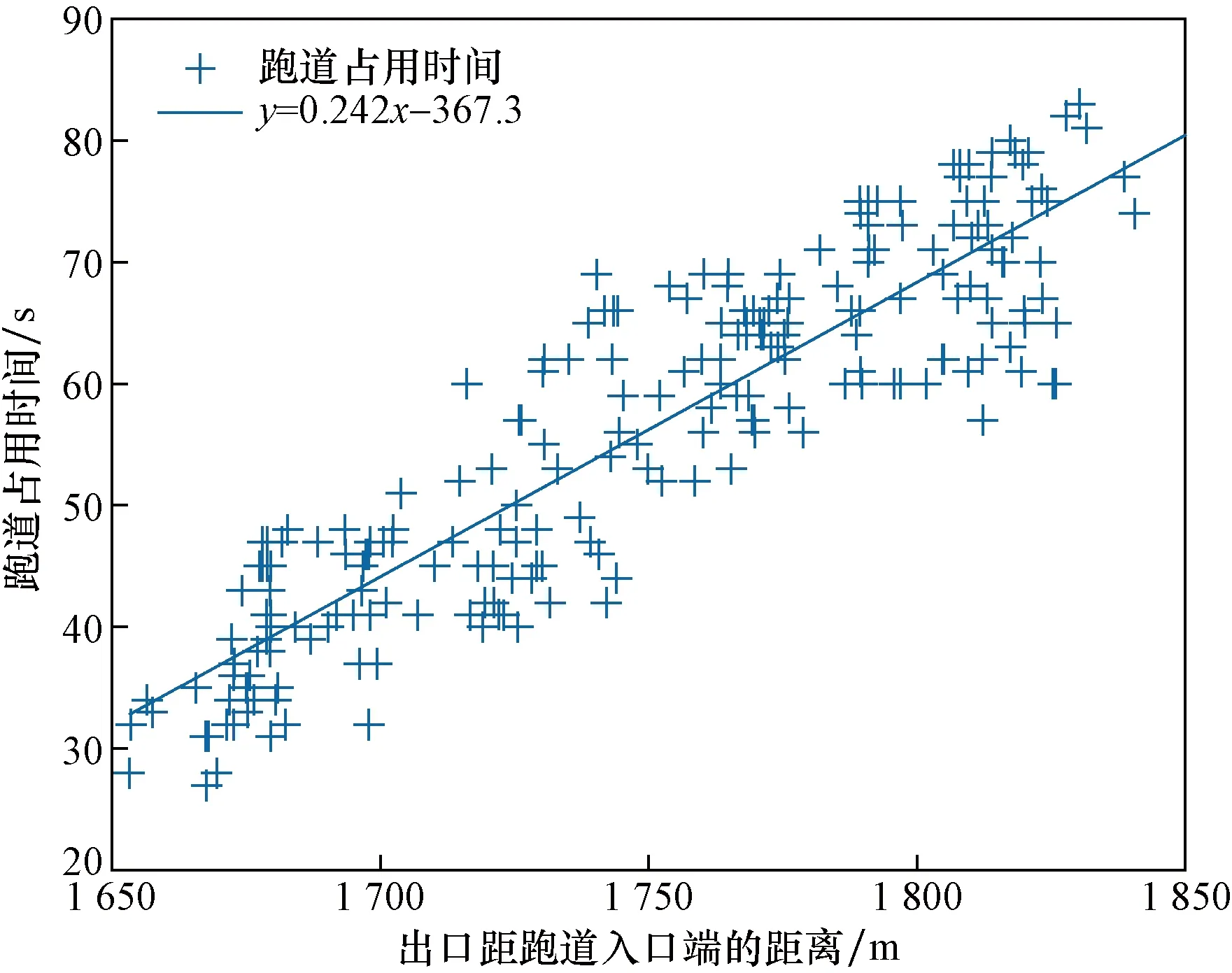
图8 跑道出口位置对ROT的影响

1.3.4 飞越跑道入口端及脱离跑道的速度

对于进近的航空器,较高的进近速度通常会导致较高的着陆速度,并缩短从跑道入口到跑道出口端所需的时间。如图9(a)所示,当航空器从同一跑道出口离开跑道时,跑道入口端速度每增加一节,跑道占用时间就会降低0.19 s。但在航空器着陆过程中,同时需要考虑到更高的进近速度会迫使航空器不能较快减速而选择更远的跑道出口,从而增加跑道占用时间。如图9(b)所示,当航空器从不同出口离开跑道时,跑道入口端的速度每增加一节,就会产生0.12 s的额外跑道占用时间。因此,如果具有不同进近速度的航空器是在同一出口离开跑道,则进近速度对ROT的影响成正比,反之则成反比。

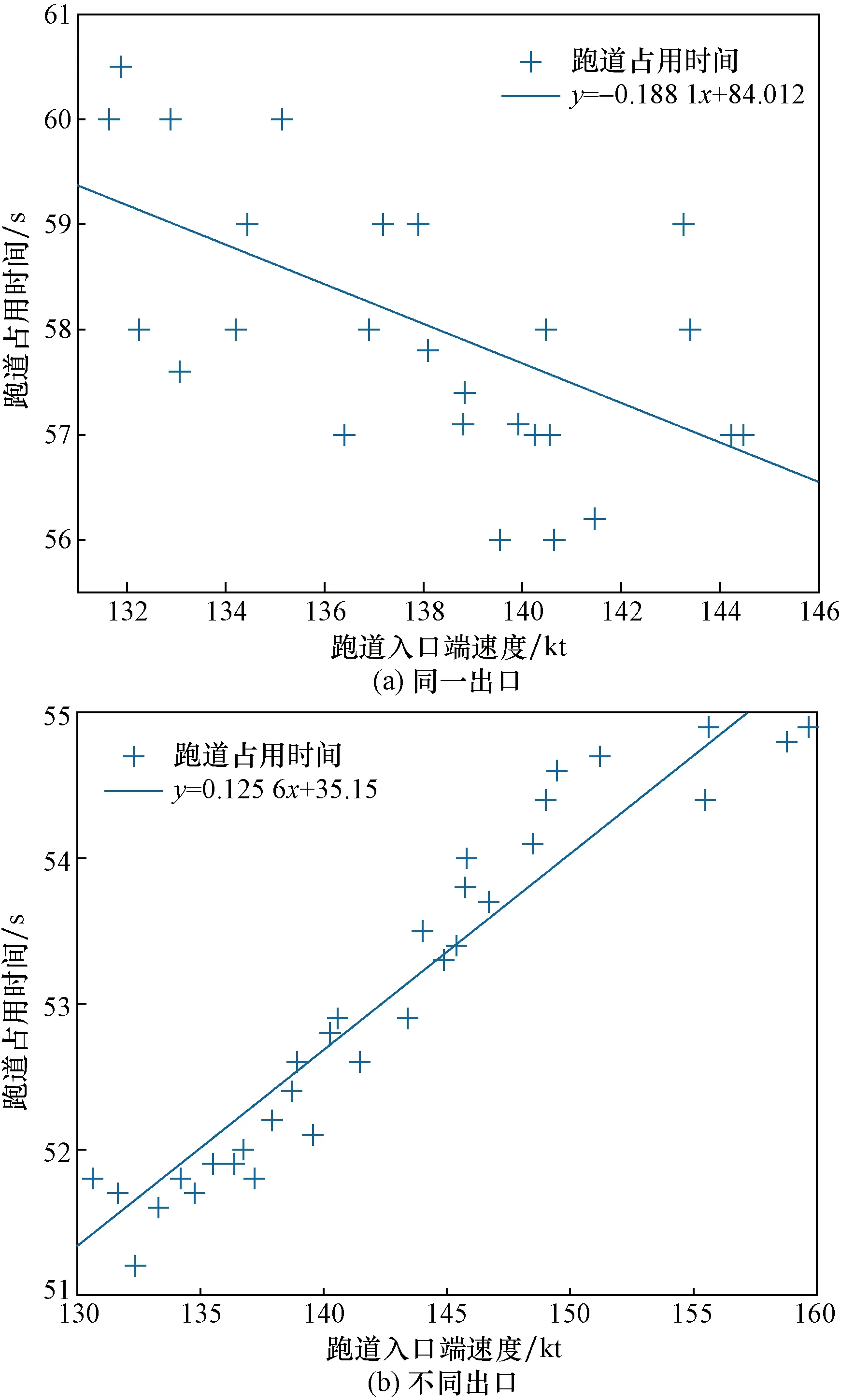
图9 跑道入口端速度对跑道占用时间的影响

1.3.5 气象条件

着陆期间的风向、风速可能会影响进场航空器的进近速度。例如,一般情况下,逆风增加航空器升力,航空器与气流的相对速度增大,跑道占用时间缩短。通过美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA),获取到纽瓦克机场每小时的天气数据(温度、风、能见度、昼夜指示器、气压高度、降水类型和数量),并与tend和t0相关联。

2 基于灰狼算法优化的进场航空器跑道占用时间预测模型

2.1 灰狼算法

灰狼算法是由 Mirjalili等[16]提出的一种智能优化算法。灰狼算法由狼群的社会等级来建模,分别为α、λ、δ和ω4种,层次结构如图10所示。

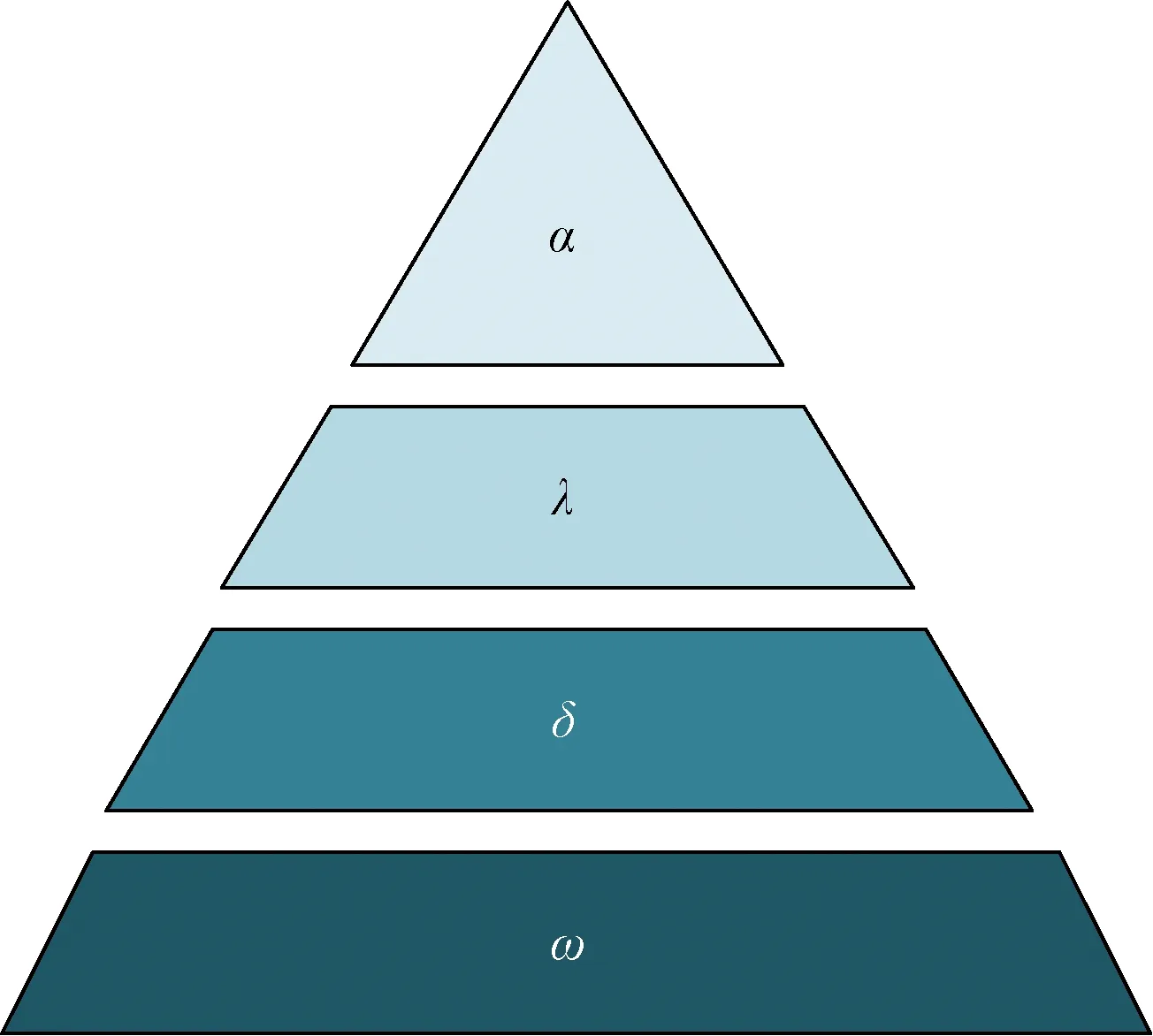
图10 灰狼等级制度

灰狼捕获猎物的过程可以用式(3)和式(4)表示。

D=|CPp(t)-P(t)|

(3)

P(t+1)=Pp(t)-AD

(4)

式中:D为灰狼与猎物之间的距离;t为当前进化代数;A和C为系数向量;Pp为猎物所处的位置向量;P为灰狼的位置向量。A和C的计算公式为

A=2an1-a

(5)

C=2n2

(6)

式中:n1、n2为[0,1]的随机向量;a为收敛因子。

灰狼逐渐接近猎物并更新其位置,ω狼更新位置和最终位置为

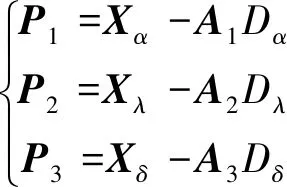
(7)

(8)

式中:Dα、Dλ、Dδ为α、λ、δ狼与猎物的距离;A1、A2、A3为α、λ、δ的系数向量;P1、P2、P3为对应狼群的位置向量;Xα、Xλ、Xδ为对应猎物的位置向量;P(t+1)为t+1时刻ω狼的位置向量。

2.2 随机森林算法

随机森林模型是一个组合分类模型,由多个决策树集成,具体构建过程如下。

(1)使用Bootstrap抽样从样本数量为N的原始数据集中有放回的随机抽取N个,作为决策树数据来训练模型。

(2)重复步骤(1)m次,得到m个新的训练集,每个训练集的大小为N。

(3)构建CART决策树,根据基尼系数Gini选择节点特征。选择基尼系数最低的阈值作为最佳分割阈值,构建决策树h(X)。

(4)训练m个样本数据集获得m棵决策树,令决策树分类序列为{h1(X),h2(X),…,hm(X)}。

(5)将每棵树对该样本的预测结果进行统计,使用投票法选出最终结果,公式为

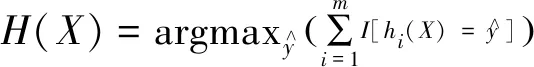
(9)

2.3 GWO优化随机森林

(1)设置狼群数量、最大迭代次数、树的个数(记为n)及最小叶子节点(记为l)取值范围。

(2) 建立随机灰狼种群,每个灰狼都有一个由n和l组成的个体位置向量。

(3) 给定初始参数n和l,使用随机森林训练样本数据,并将个体的适应度表示为训练集的识别准确率。

(4) 计算每只灰狼的适应度值,根据适应度值将灰狼分为α、β、δ和ω4个等级,并更新每个个体在灰狼群体中的位置。

(5) 若迭代次数超出最大迭代次数,寻优结束,得到最优参数n和l;否则跳转至(4)继续进行参数寻优,得到最优的随机森林分类模型。

算法流程图如图11所示。

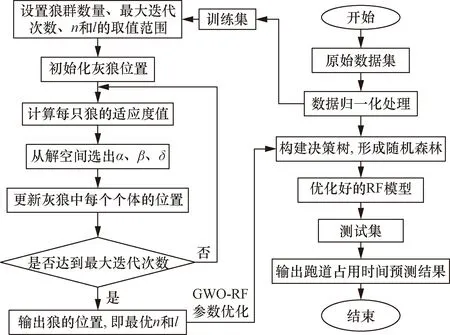
图11 GWO-RF模型流程图

2.4 模型试验结果与分析

对跑道出口选择、跑道出口角度、气象条件、跑道入口端速度、跑道出口端的速度、机型、航空公司7个变量建立机器学习模型,对进场航空器跑道占用时间进行建模。

2.4.1 寻优过程分析

在提取跑道占用时间后,使用GWO寻找RF最佳参数。GWO的初始化设置和RF参数取值范围如表3所示。

表3 航空器跑道占用时间统计分析

RF参数寻优适应度曲线如图12所示,可以看出:经过3次迭代后,适应度函数大幅度下降保持在0.195;经过8次迭代后,最佳适应度保持在0.194。相比人工随机选择参数相比, GWO可以增加寻优的效率和准确率。经过寻优,得到最佳树的个数取值为49、最小叶子节点取值为2。

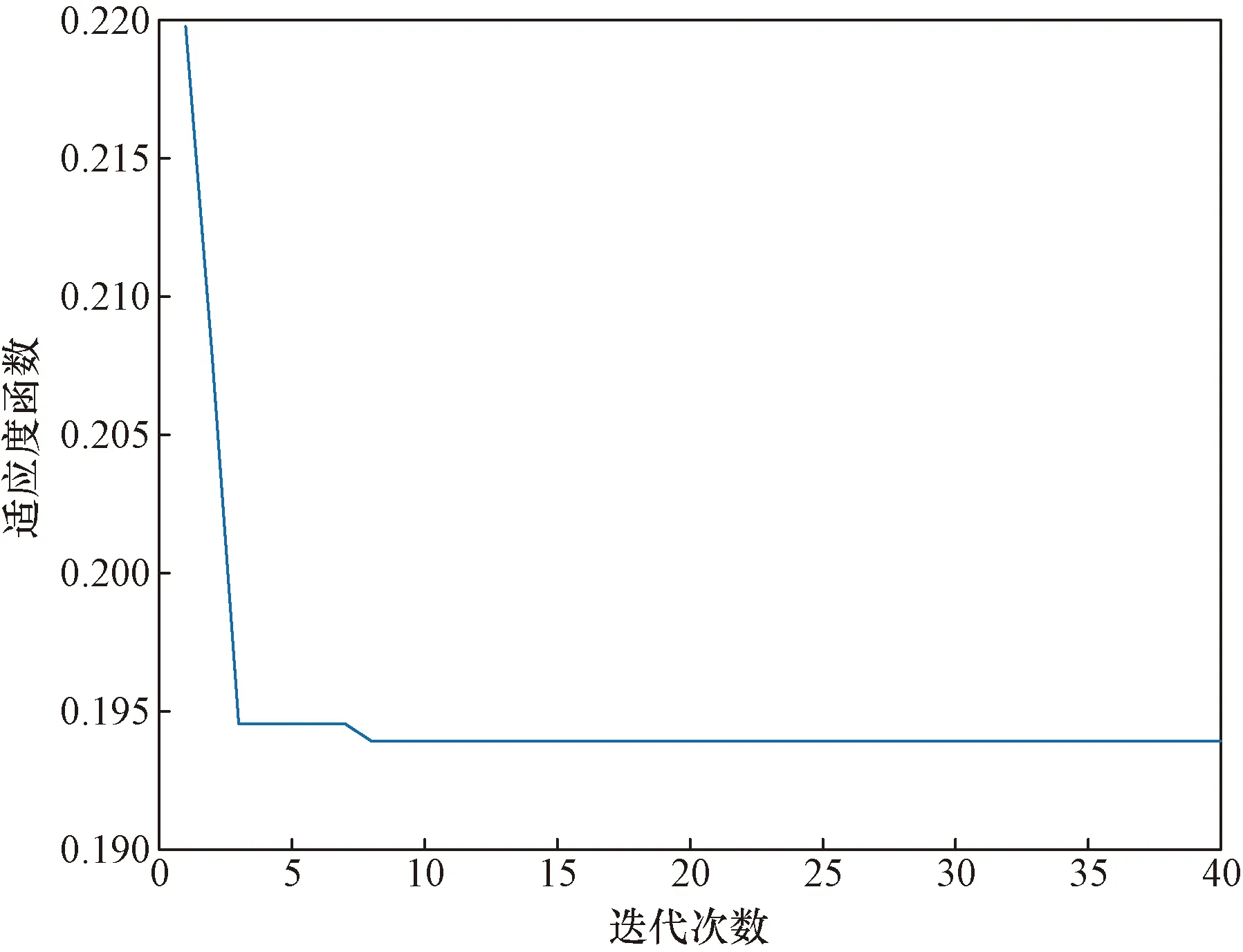
图12 GWO-RF参数寻优适应度曲线

利用上述随机森林模型研究ROT,该过程类似于数据分析中的曲线拟合过程,为了论证预测结果的准确性,选择平均绝对误差(mean absolute error,MAE)、均方根误差(root mean squared errors,RMSE)作为评价指标,其中MAE为4.020 7、RMSE为4.443 7。并使用回归分析来估计模型的鲁棒性,选择R2参数进行真实值和预测值之间的回归分析。图13显示了优化后的RF模型ROT预测回归图,对实际值和预测值进行回归分析,可以看出随机森林模型完成了预测分析,且没有出现过拟合情况。

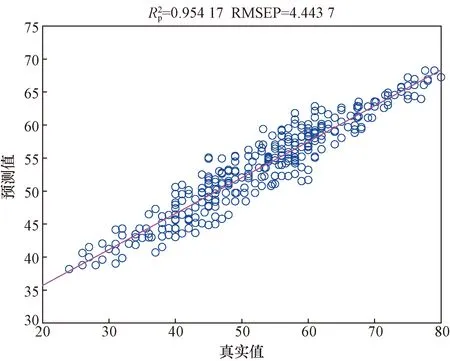
图13 跑道占用时间真实值预测值回归图

2.4.2 影响跑道占用时间的因素分析

通过随机森林回归算法确定影响跑道占用时间的因素。通过查看每个树的每个节点对降低数据集总方差的贡献程度,可以确定每个因素在ROT估计中的重要性排名,并对影响因素进行了排序。

图14给出了影响跑道占用时间因素的排名。在该排名中可以看出,航空器用于滑出跑道的出口选择占主导地位,占变化量的25.95%;跑道出口端速度和跑道入口端速度对跑道占用时间均有显著影响,占变化量的17.28%和16.39%;天气因素、机型、跑道入口角度对跑道占用时间的影响接近,占变化量的12.61%、9.96%和9.35%;最后,航空公司因素对跑道占用时间的影响较小,占变化量的8.46%。

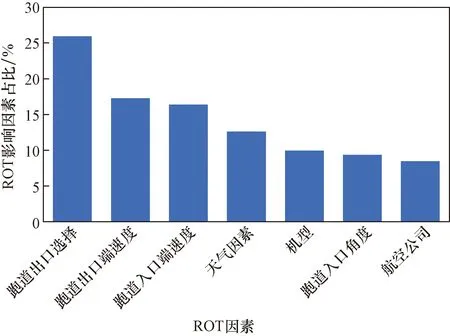
图14 ROT影响因素重要性排名

2.4.3 模型准确度对比

提取得到的100个预测值与实际值进行了比较,图15显示了与实际值相比预测值的准确性。由图15可知,预测值和实际值基本重合,表明模型的拟合效果很好。

图15 不同模型预测准确率对比

模型的准确性可以用±5 s、±7 s和±10 s这3个指标及误差图来评价。准确率定义为在一定范围内的模型预测时间与实际跑道占用时间的差值数量与总样本数量之比。例如,±5 s的准确率是指实际时间与模型预测时间不超过5 s的样本数占实际样本总数的百分比。表4显示了预测值和准确值之间的误差,对比结果显示优化后的随机森林模型对纽瓦克机场进场航空器跑道占用时间的预测结果与实际结果在±7 s的准确性平均达到88.08%,已经超过现有研究的准确性。44～63 s为航空器跑道占用时间的第25百分位数至第75百分位数,但还存在航空器在进场时受空中交通管制、极端恶劣天气影响、机场拥堵等不常见原因导致跑道占用时间过长或过短的现象,总体跑道占用时间为20～145 s,在此情况下再引入±10 s作为评价指标,10 s的误差占比不大符合实际运行效果,模型±10 s的准确性达到93.59%。这表明使用GWO-RF算法的进场航空器跑道占用时间预测模型更合适。

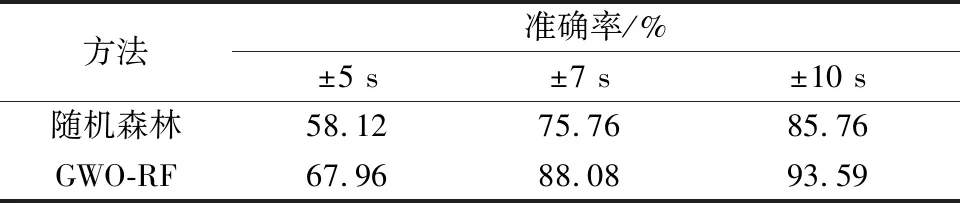
表4 模型预测准确率对比

3 结论

(1)通过对跑道占用时间的分析,可以发现跑道出口的选择对ROT的影响最大,跑道出口端速度、跑道入口端的速度、气象情况、机型、跑道出口角度、航空公司等因素也对跑道占用时间具有不同程度的影响。

(2)通过GWO实现了随机森林参数的高效寻优,提升了随机森林参数的优化效率,使得 ROT预测模型具有良好的准确性和鲁棒性。

(3)在未来跑道占用时间的预测工作中,可以考虑将跑道因素、特殊天气因素引入进行建模,以进一步提高跑道占用时间的准确性,为管制员提供更加高效、准确的决策信息。