盾构下穿引起上覆管线变形的解析计算方法

王晓军

(中铁十一局集团有限公司, 武汉 430061)

尽管盾构掘进技术已经较为成熟,但在隧道开挖过程中,打破了地层中原始应力平衡状态,从而使得周边土体产生了相应的自由位移场,进而会引起上覆管线应力应变响应[1-5],严重时会引起管线管片开裂、渗水、断裂。

目前,针对盾构隧道对邻近隧道及管线受力变形影响的理论主要基于两阶段法,第一阶段可以采用Peck公式[6]或者Loganathan公式[7]来评估隧道开挖对周边土体变形的影响,第二阶段将既有隧道或者管线简化成梁搁置在不同地基模型上,通过解方程的方法获得其受力变形解析。梁荣柱等[8]基于Winkler地基和铁木辛柯梁,获得了考虑剪切变形下隧-土相互作用半解析解;张陈蓉等[9]基于Winkler地基模型及管线接口非线性的工程实况,通过解析获得既有管线在盾构开挖下受力变形响应;然而,相比于Winkler地基,两参数Pasternak和Vlasov地基由于能够考虑土体剪切变形影响而更广泛地应用于地下工程中[10-11]。张桓等[12]基于Pasternak地基和管线侧向土体影响对管-土相互作用的影响,通过解析解的方法获得管线在隧道下穿影响下的理论解析;Liang等[13]基于欧拉梁和Pasternak地基,获得非线性土体反力作用下新建隧道引起上覆管线受力变形差分解;何小龙等[14]基于Pasternak地基模型并考虑管-土分离的工况,解析获得管线在邻近基坑开挖作用下受力变形响应。章李刚等[15]基于Pasternak地基模型,并考虑到管廊存在残余顶推力的工况,通过差分的方法获得管廊在盾构下穿作用下的受力变形响应。同时,也有学者采用双参数的Vlasov地基模型[16]和三参数Kerr地基模型[17-20]模拟隧-土相互作用,但考虑到Kerr地基模型参数较多,公式复杂繁琐,难以用于实际工程中。

综上所述,双参数地基模型简单且实用于预测管-土相互作用,并能较好地反映管线在邻近开挖作用下的影响,但以上理论均是基于力学平衡的角度出发,而忽视了管线在受力变形过程中系统的能量关系。基于此,现从能量法的角度出发,采用Pasternak地基建立管线在外力作用下的势能方程,并利用最小势能原理对管线能量进行变分求解,随后获得盾构下穿引起上覆既有管线受力变形解析解。最后将该方法与工程实测数据进行对比验证并展开一系列参数分析。

1 分析方法

1.1 理论解析过程

如图1所示,将既有管线简化为搁置在Pasternak地基模型上的无限长梁,并做出如下假设:①假定既有管线为抗弯刚度EI、直径D的圆形截面无限长梁搁置在Pasternak地基模型上;②梁和地基都处在弹性变形的阶段内,既有管线与周围土体协调变形;③既有管线轴线处的附加荷载为q。

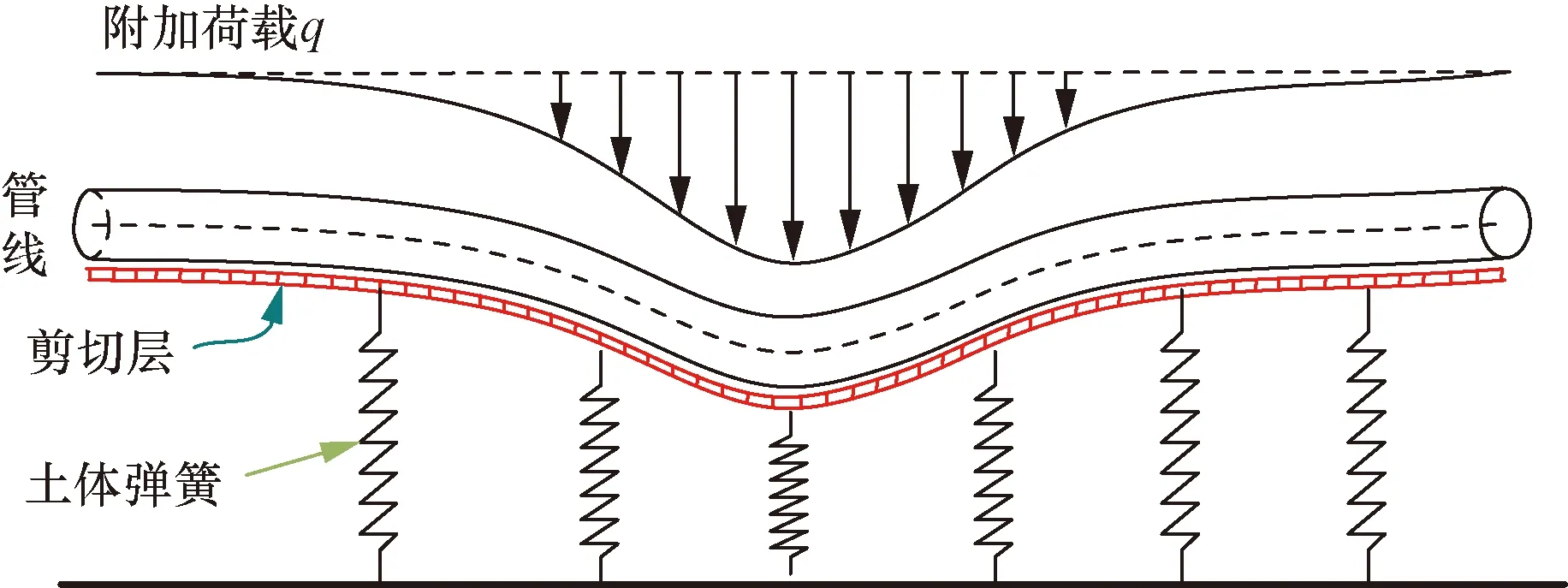
图1 Pasternak地基模型

Pasternak地基模型下管线所受土体反力为

(1)

式(1)中:w(x)为管线竖向位移;p(x)为既有管线所受土体反力;k为地基弹性刚度;G为地基剪切层刚度。k和G的计算公式为

(2)

式(2)中:υ和Es分别为土体模量和泊松比;D为既有管线直径;t为土体剪切层厚度,t=2.5D。

为了采用能量法求解既有管线变形位移,根据Rayleigh-Ritz法[21]假设管线位移函数满足:

(3)

式(3)中:Ai为待定系数;w为管线竖向位移;L为一半管线长度;ai为待定系数;x为沿管线纵向方向的坐标值;i=0,1,2,…,n。

式(3)可简化为

w={B}1×(n+1){A}(n+1)×1

(4)

式(4)中:

(5)

考虑到管线变形总能量分为弯曲变形能E1、Pasternak模型中地基反力作用功E2和附加荷载q作用功E3,其计算公式分别为

(6)

基于能量变分法可知:

δE1+δE2+δE3=0

(7)

分别对管线弯曲变形能E1、地基反力作用功E2以及附加应力作用功E3进行变分计算:

(8)

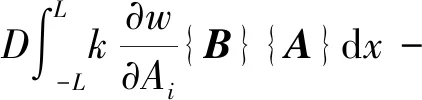
(9)

(10)

则式(7)可转化为

(11)

将式(11)进一步写为矩阵方程的形式,即

(K1+K2-K3)A=q

(12)

式(12)中:K1为管线弯曲刚度矩阵;K2为土体弹性刚度矩阵;K3为土体剪切刚度矩阵;q为附加应力向量。K1、K2和K3的表达形式分别为

(13)

(14)

(15)

将式(13)～式(15)代入式(12),可求解得到待定系数向量{A}的表达式,随后将其代入式(3)即可得到管线竖向位移w的表达式。

同时,管线所受弯矩和剪力的微分控制方程为

(16)

(17)

至此,得到盾构下穿引起上覆管线变形w(x)位移及其内力解析解。

1.2 自由位移场求解

基于Loganathan等[7]提出邻近土体随隧道开挖下自身自由位移重分布的表达式为

(18)

式(18)中:R为隧道半径;H为隧道轴线深度;x为管线到隧道中心线的水平距离;z为距地表垂直距离;ε为等效地层损失比;υ为土体泊松比。

根据既有文献[3]的研究可知,当隧道和管线存在夹角θ时,式(18)中x将变成xsinθ,且盾构下穿对上覆既有管线轴线处产生的附加荷载为

(19)

2 算例验证

2.1 工程概况

吴为义[22]曾报道深圳地铁一期工程隧道盾构下穿既有上覆管线的工程实况(图2),同时,在施工过程中监测既有管线在隧道开挖下结构的变形位移,其中管线埋深为z0,根据吴为义[22]的研究,既有管线变形监测布置如图3所示,且新建隧道和既有管线的参数以及两者之间的土体参数信息如表1所示。

表1 工程实例计算参数

图2 隧道与管线位置简图

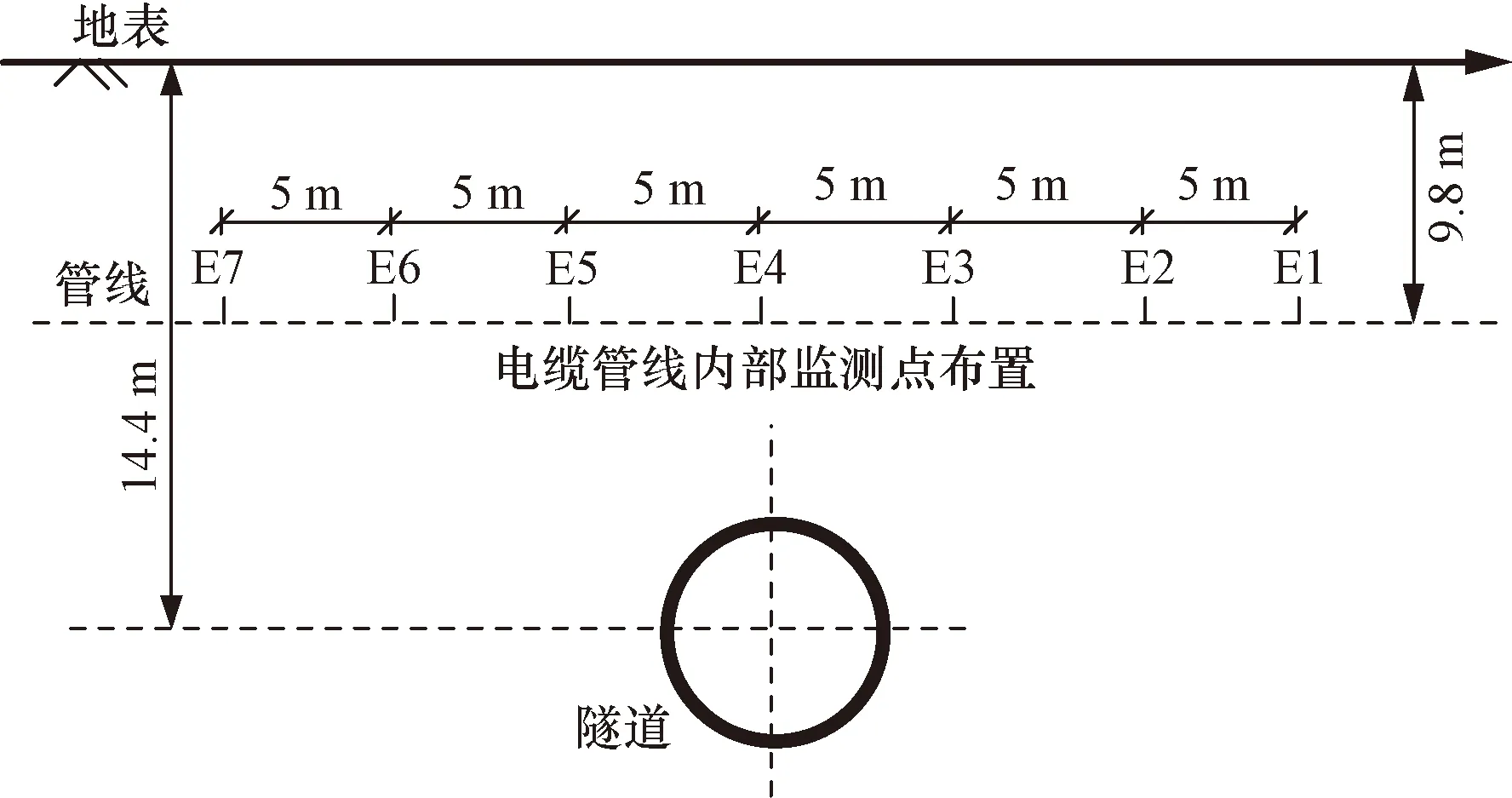
图3 管线测点布置图

2.2 计算结果分析

采用本文方法和传统计算方法计算本案例的管线变形数据与实测数据对比如图4所示,其中传统计算方法指的是指基于力学平衡理论采用有限差分法获得将既有管线简化为欧拉梁搁置在Pasternak地基和Winkler地基(E-P和E-W模型)上的半解析解。由于实测数据仅分布在管线轴线两侧20 m范围内,同时为了展示3种方法与实测数据的比较,采用3种方法计算了管线中心轴线两侧40 m范围内的变形数据,并对计算结果与实测数据进行对比分析。由图4可见,3种方法计算结果与实测数据分布一致,呈现出管线中心轴处变形最大,后逐渐向两侧减小的趋势。在盾构下穿作用下,既有管线主要变形范围分布在管线中心轴线两侧20 m范围,此时管线变形实测数据均大于2 mm,这也是既有管线最容易产生破坏的区段,而本文方法结果与实测数据相近,能够较好地拟合管线变形的实测数据。采用本文方法获得管线最大变形位移为7.95 mm;采用差分解获得的E-P模型计算结果偏大,其解析获得管线最大变形为9.1 mm;同样地,采用差分解获得的E-W模型计算结果更大,其计算的管线位移峰值为14.4 mm。本文方法采用的能量法相比于差分法的计算结果,能充分考虑到土体的剪切效应,导致其预测结果更贴合工程实际;而Winkler地基缺乏考虑土体剪切效应,其计算结果明显偏大。总的来说,本文方法能够较好地反映实际工程中的管-土相互作用。

图4 管线计算变形及实测数据对比曲线

采用本文方法、E-P和E-W方法计算获得盾构下穿作用下管线内力分布如图5所示。由图5可知:本文方法和E-P计算结果相差不大,这是由于两者都考虑到了土体剪切变形的影响,但其相比于差分法求解管线变形,本文研究采用的能量计算方法法低估了盾构下穿对邻近既有管线的影响;然而,E-W模型由于缺乏考虑土体剪切效应对管-土相互作用的影响,其计算结果明显偏大。

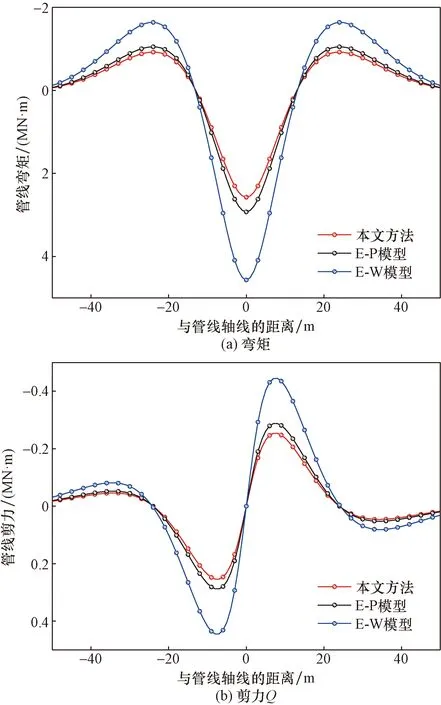
图5 管线内力分布图

3 参数分析

为了研究盾构开挖半径,地层损失率和隧道和管线夹角变化对上覆既有管线受力变形的影响,仍以第2节深圳地铁一期工程作为基础数据,并基于变量分析法进行参数分析。

3.1 盾构开挖半径

不同盾构开挖半径下既有管线变形及其弯矩分布图如图6和图7所示。从图6和图7可以看出,在盾构下穿作用下既有管线变形和弯矩沿管线中心轴线对称分布,且管线变形和弯矩峰值处均位于管线中心轴线。同时,既有管线变形及内力随盾构开挖半径增大而呈现出逐渐增大的趋势,且其增速也逐渐增大。造成这一原因在于随着盾构半径的增大,管线与隧道之间的竖向净距越来越近且增大的开挖半径致使隧道开挖引起的周边土体自由位移逐渐增大,最终导致既有管线轴线处的位移及其内力也会呈现出快速增大的变化。由此可知,在实际工程中,尽量减小盾构开挖半径以减轻盾构下穿对邻近既有管线受力变形的影响。

图6 不同盾构半径下管线变形分布

图7 不同盾构半径下管线弯矩分布

3.2 地层损失率

不同地层损失率下盾构开挖引起上覆管线纵向位移峰值wmax和弯矩峰值Mmax变化分布如图8和图9所示。从图8可知,随着地层损失率从0.5%增加到2.5%的过程中,管线最大变形位移从4.7 mm逐渐递增到23.7 mm,增幅高达4.0倍,且其增长速率基本无变化。从图9可知,随着地层损失率的逐渐增大,既有管线弯矩峰值从1.34 MN·m增大到6.68 MN·m,其增幅3.99倍,且其增长速率基本保持恒定。产生这一现象说明在盾构下穿作用下,既有管线变形及其内力与地层损失率保持线性增长的关系,这也说明地层损失率是决定管线受力变形的关键因素。

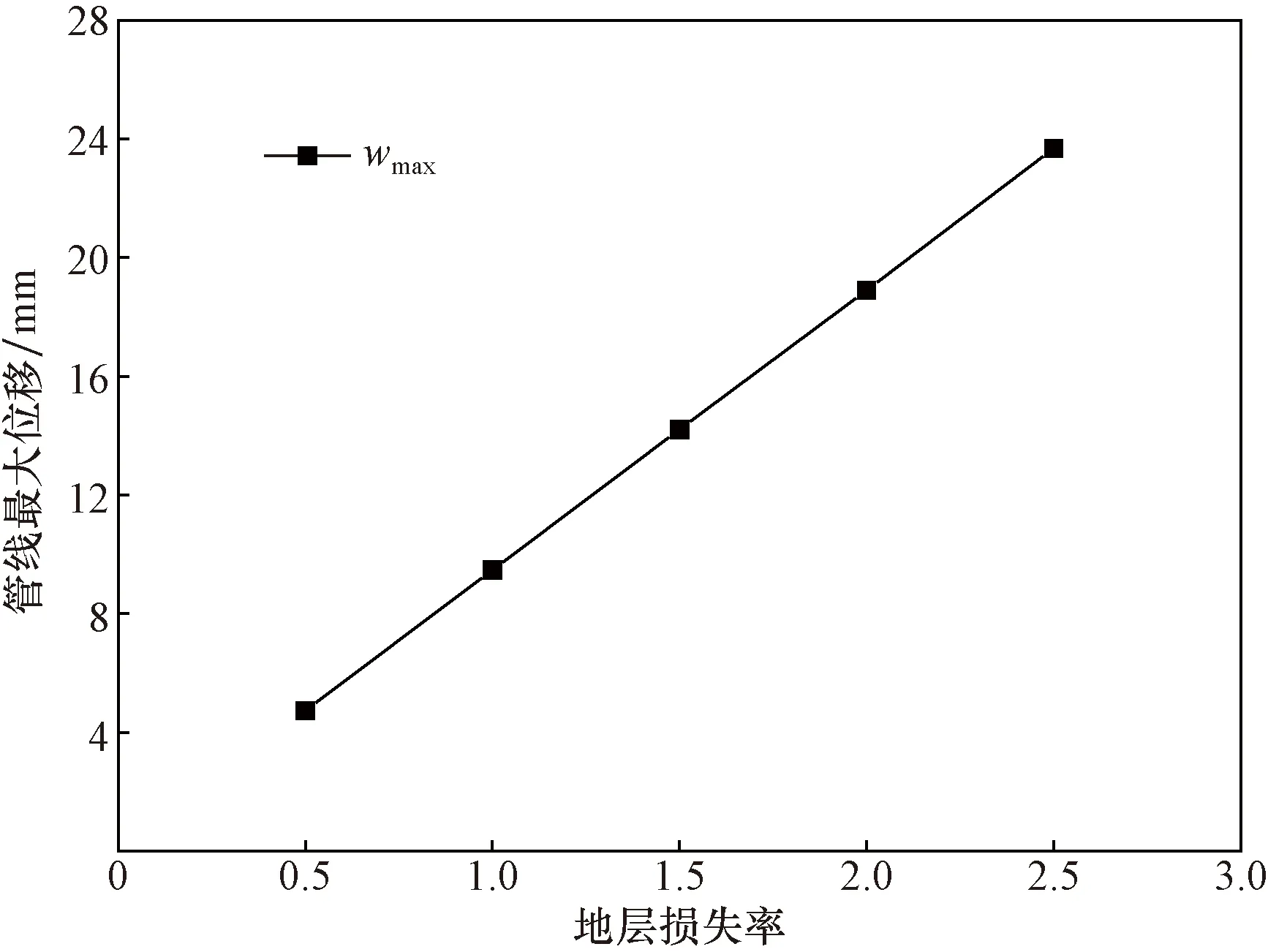
图8 不同地层损失率下管线变形峰值变化

图9 不同地层损失率下管线弯矩峰值变化

3.3 隧道与管线夹角

不同隧道与管线夹角下既有管线变形峰值wmax和弯矩极值Mmax变化如图10和图11所示。从图10可知,当隧道与管线夹角从15°增大到90°时,管线变形峰值从14.26 mm逐渐减小到7.96 mm,降幅约为44%,且其减小速率迅速变缓。然而,从图11可知,随着隧道与管线夹角逐渐增大,管线弯矩峰值从0.82 MN·m逐渐增大至2.24 MN·m,增幅近1.73倍,且其增长速率也迅速变缓。笔者认为这是由于随着两者相对位置从较为“重合”转变成“垂直”状态,隧道开挖对管线轴线处产生的土体自由位移逐渐变小,且管线受到的附加荷载从“均布荷载”转变成“集中荷载”的状态,管线所受最大附加应力反而会增大。这也说明两者夹角对既有管线受力变形不可忽略,在实际工程中也要注意隧道与管线的夹角对管线的影响。

4 结论

基于能量法提出了一种可预测既有管线在盾构下穿作用下受力变形的解析计算方法。得到如下结论。

(1) 基于能量法,采用Pasternak地基模拟管-土相互作用,考虑管线在外力作用下系统总势能结合变分法获得盾构下穿引起既有上覆管线受力变形解析计算方法。

(2) 与深圳某隧道工程监测数据对比,本文方法获得的管线变形位移与实测接近,计算精度高。相比于传统力学特性下的Pasternak和Winkler地基差分解比较,本文方法更贴近实测。

(3)参数分析表明:盾构半径和地层损失率的增大会引起管线受力变形的迅速增大;而增大隧道与管线的夹角会减轻管线变形但会使得管线弯矩增强,其速率逐渐变缓。