铁路波纹钢管涵力学特性数值仿真及参数分析
许见超 董亮 随意 班新林
中国铁道科学研究院集团有限公司 铁道建筑研究所, 北京 100081
波纹钢管涵不仅具有施工便捷、工期短、运输方便等优点,而且对基础承载力要求较低,适应变形能力强,适用于山区、特殊土体等区域的涵洞工程。波纹钢管涵在我国公路工程领域应用较多,在铁路工程中仅青藏线采用了4 座波纹钢涵洞,其推广应用尚待研究。
指导波纹钢管涵设计的规范主要有美国规范[1]、加拿大规范[2]和中国规范[3],指导波纹钢管涵使用的手册有文献[4-6]等。在波纹钢涵洞上覆恒载土压力计算方面,加拿大规范[2]和中国规范[3]考虑了土-结构相互作用,引入了结构起拱效应产生的土压力增大系数(kf),同时通过轴向刚度参数(Cs)考虑波纹钢涵洞和回填土相对刚度的影响;而美国规范[1]对此处理相对简单,一般认为恒载土压力是涵顶填土的棱柱体重量。在结构内力分析和强度检算方面,各国规范均基于环向压力理论,美国规范[1]检算了管壁受压强度和屈曲应力,加拿大规范[2]和中国规范[3]则进一步检算了塑性铰。
针对波纹钢涵洞的研究主要集中在公路工程领域,对铁路波纹钢管涵的系统研究尚不足。本文通过建立铁路波纹钢管涵受力分析有限元模型,将列车荷载按客货共线铁路特种荷载考虑,系统分析铁路波纹钢管涵的受力特征及涵顶填土高度、列车荷载作用位置、填土弹性模量、壁厚、管径、波形等关键结构参数对波纹钢管涵受力的影响规律,为波纹钢管涵在铁路工程中的应用提供技术支撑。
1 数值模型建立
建立的波纹钢管涵受力分析数值模型,见图1。波纹钢管内径3 m,波形为150 mm(波长) × 50 mm(波高),壁厚4 mm,填土高度2 m,截取2个完整波形。根据文献[14]研究结果可知,柔性管涵受3 倍管径以外的土体影响较小,故模型中截取管涵左右两侧各9 m、底部向下9 m 范围内的土体。约束模型底部三向平动自由度,约束模型侧面法向平动自由度。考虑到柔性管涵在施工过程中对管周回填土体有严格的压实要求,荷载作用下土与管涵之间不会产生明显的相对滑动,本文对埋置管涵与周围土体之间的接触方式采用绑定约束进行模拟。该简化方式已被许多学者应用[15]。

图1 波纹钢管涵有限元模型
土体采用实体单元C3D8R 离散,波纹钢管采用S4R壳单元离散,土体与波纹钢管接触局部加密网格。在工程应用中,波纹钢管涵自身及周围土体基本处于弹性状态,波纹钢和土体本构均采用弹性模型。TB 10001—2016《铁路路基设计规范》[16]中规定了各类基床填料的地基系数(K30)。参考文献[17],依据弹性均质半无限体空间理论(BOUSSINESQ),得到地基弹性模量(Ev)和地基系数(K30)的相关关系。经换算,K30为80 ~ 190 MPa/m,Ev为17 ~ 41 MPa。数值模型材料参数见表1。

表1 数值模型材料参数
根据TB 10002—2017《铁路桥涵设计规范》[18],客货共线铁路涵洞设计采用ZKH特种荷载(图2)。列车荷载经道床传至路基表面,道床厚度按0.3 m 计,荷载在道床中的扩散角度正切值取0.5,则特种荷载在路基表面的线路方向分布长度为1.4 × 3 + 0.3 = 4.5 m。列车荷载在线路横向的分布宽度为2.9 m。根据TB 10002—2017 最不利工况,动力系数取1.4,则特种荷载在路基表面的分布集度为1.4 × (250 × 4)/(4.5 ×2.9) = 107.2 kN/m2。根据TB 10002—2017,道床轨道结构自重荷载集度取19.1 kN/m2。列车荷载施加在涵顶,线路方向分布长度为4.5 m。首先施加管涵截面中心高度以上土体的自重荷载,再施加道床轨道结构自重,最后施加列车荷载。
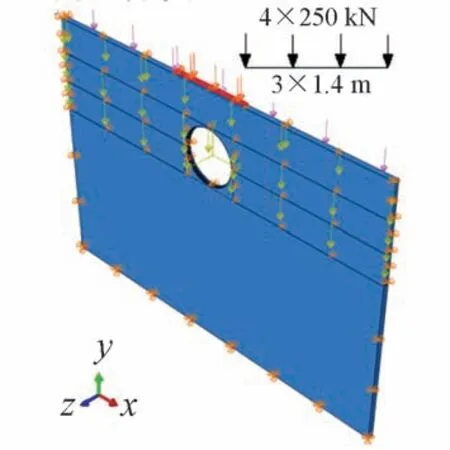
图2 施加列车荷载
2 波纹钢管涵受力特征
2.1 管涵涵身环向应力分布
管涵环向应力分布见图3。图中,环向位置为0°时对应涵顶。可知:管涵在恒载和活载作用下的环向应力分布特征基本一致,管涵在承受整体环向压应力的同时,在涵顶、涵底和两侧存在显著的弯曲应力。涵顶、涵底的波峰受压,波谷受拉,管涵两侧波峰受拉,波谷受压。管涵4个45°位置的环向应力基本为压应力。涵身最大绝对值对应的应力为压应力。
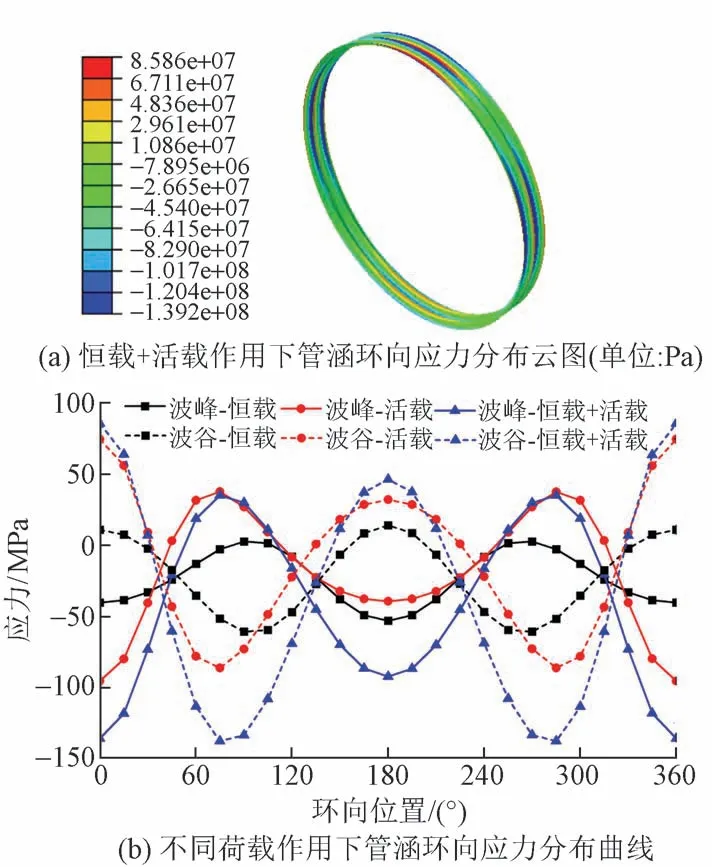
图3 管涵环向应力分布
2.2 涵周土压力分布
涵周土压力分布见图4。可知:涵周土压力均为压应力;管涵波峰处土压力明显大于波谷处;管涵顶部、底部土压力小于管涵两侧土压力,说明荷载作用下管涵横向膨胀挤压土体,与土体之间存在显著的结构-土相互作用。
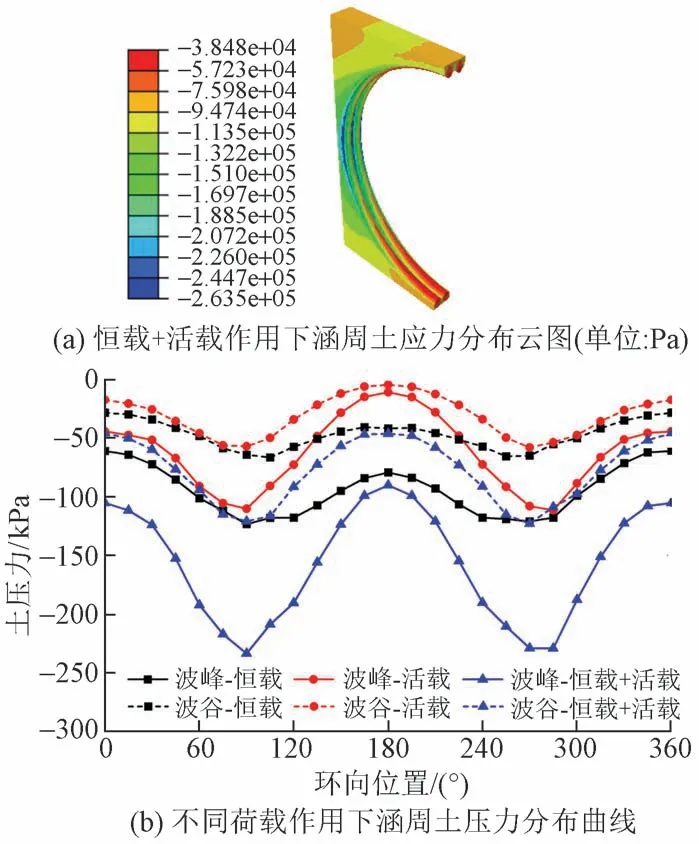
图4 涵周土压力分布
3 波纹钢管涵受力参数分析
3.1 填土高度
保持数值模型中其他参数不变,计算涵顶填土高度分别为0.6、1.0、2.0、4.0、7.0、10.0 m 时的管涵受力响应。不同填土高度下管涵最大应力变化曲线见图5。可知:随着填土高度的增加,恒载作用下管涵最大环向拉、压应力线性增加;活载作用下管涵应力逐渐减小;恒载+活载作用下,管涵最大压应力逐渐增大,最大拉应力逐渐减小。
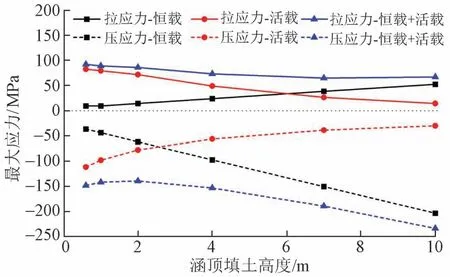
图5 不同填土高度下管涵最大应力变化曲线
不同填土高度下涵顶土压力变化曲线见图6。可知:涵顶波峰处土压力显著大于波谷处土压力;随着填土高度的增加,路基自重下涵顶土压力线性增加;涵顶波峰、波谷土压力均值小于涵顶土柱自重应力。
小学语文是众多学科里面比较重要的一门学科,教材中的任何一篇课文都是需要学生了解其中的主旨内涵,在思维发散中获得语文的多重感悟。教学中对微课的应用非常符合当下小学生的特点,打破了死气沉沉的语文课堂。因此老师应该顺应时代的改变,使微课的优势在课堂中最大化,转变传统的教学观念,把学生从旁观者状态脱离出来,在语文学习中融入自己的情感与作者产生共鸣。微课不仅图文并茂,还能够在网络中获取大量的辅助信息,在课堂中教师可以根据学生的实际情况,打破传统的教学模式,把语文教学内容充实起来,把微课作为载体,促进语文教学质量的有效提升。
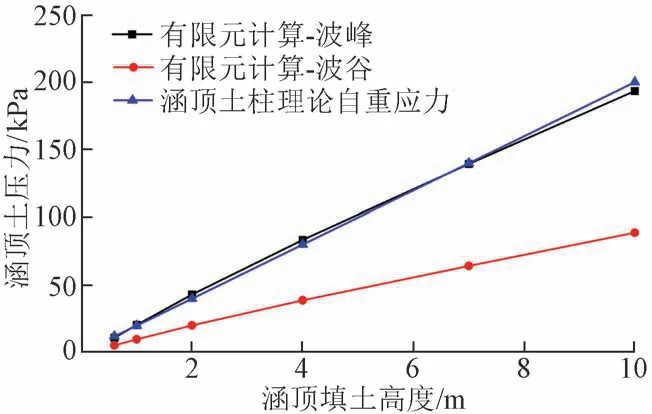
图6 不同填土高度下涵顶土压力变化曲线
不同填土高度下管涵竖向活载挠度见图7。可见,活载作用下,随着填土高度的增加,管涵竖向挠度减小,活载作用效果减弱。
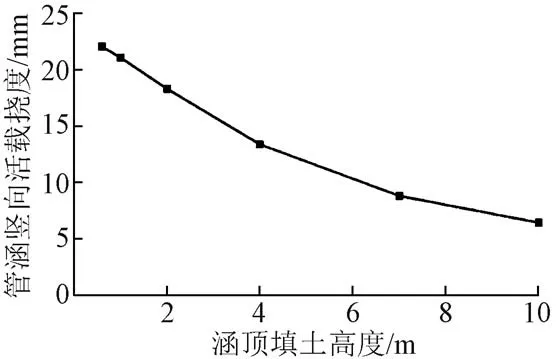
图7 不同填土高度下管涵竖向活载挠度
3.2 列车荷载作用位置
保持数值模型中其他参数不变,计算涵顶填土高度为0.6、2.0、4.0 m,活载作用位置由x= 0(涵顶正上方)移动至x= 6.8 m 时恒载 + 活载作用下管涵环向最大拉、压应力。活载移动步长为0.2 m,向模型左侧(环向270°方向)移动;活载中心作用于管涵边界时,x= 1.5 m;活载全部退出管涵时,x= 3.8 m。管涵环向最大拉、压应力随活载作用位置变化曲线见图8。
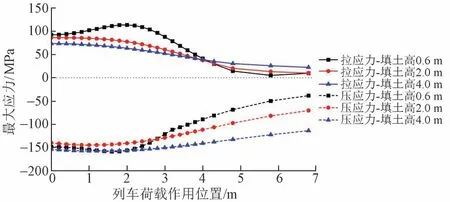
图8 管涵环向最大应力随活载作用位置变化曲线
由图8可知:
1)涵顶填土高度为0.6 m 时,随着活载作用位置逐渐远离涵顶正上方,管涵最大环向压应力和拉应力均先增加再减小。x= 1.6 m 时最大环向压应力取得最大值-158.0 MPa,比x= 0时增大6.8%;x= 2.0 m时最大环向拉应力取得最大值113.2 MPa,比x= 0 时增大23.0%
2)涵顶填土高度为2.0、4.0 m 时,随着活载作用位置逐渐远离涵顶正上方,管涵最大环向压应力先小幅增加再减小;管涵最大环向拉应力减小。填土高度为2.0 m,x= 1.0 m 时最大环向压应力取得最大值-144.2 MPa,比x= 0 时增大了3.6%。填土高度为4 m,x= 1.2 m 时,最大环向压应力取得最大值-157 MPa,比x= 0 时增大了2.5%,两种工况增幅均很小。
综上,涵顶填土高度为0.6、2.0、4.0 m 时,活载中心作用于接近管涵边界或管涵正上方和边界之间某位置时,管涵取得最大环向压应力,但数值与活载中心作用于涵顶正上方时相差很小(差值小于等于6.8%)。
以填土高度2 m 工况为例,绘制不同活载作用位置时管涵波峰环向应力分布曲线和涵周土压力分布曲线,见图9。可知:随着活载作用位置的变化,活载作用下管涵的环向应力及涵周土压力分布曲线形状一致,但会跟随活载位置的变化发生平移。
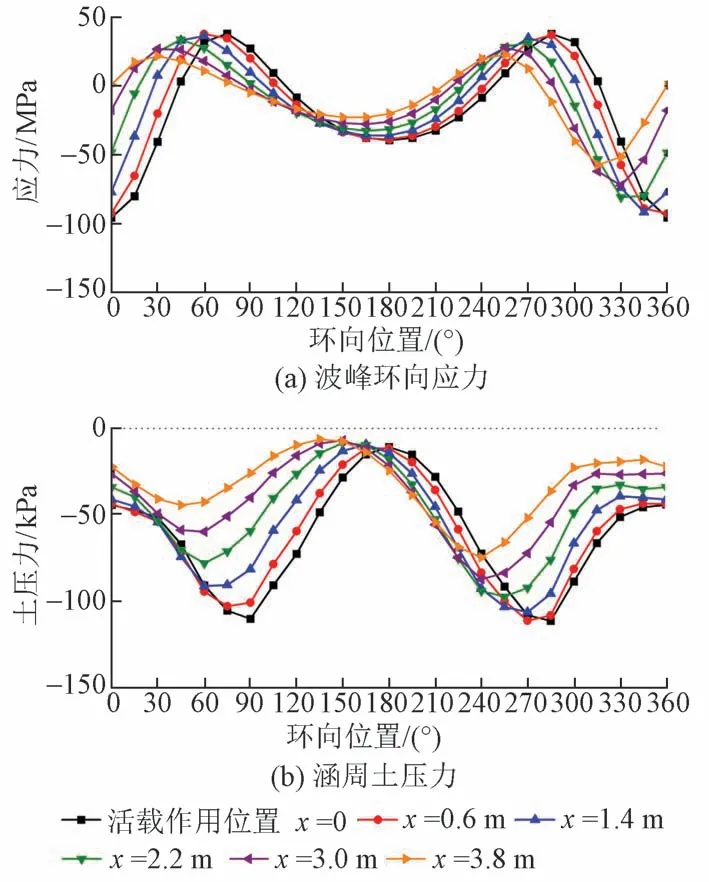
图9 不同活载作用位置管涵应力、土压力分布曲线
不同活载作用位置时管涵活载挠度变化曲线见图10。可知:涵顶填土高度为0.6 m时,随着活载作用位置逐渐远离涵顶正上方,挠度先略微增大再减小;涵顶填土高度为2.0、4.0 m 时,随着活载作用位置逐渐远离涵顶正上方,管涵活载挠度逐渐减小。
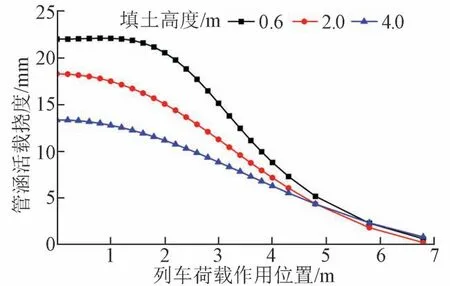
图10 不同活载作用位置管涵活载挠度变化曲线
3.3 填土弹性模量
保持数值模型中其他参数不变,计算填土弹性模量取6、12、17、34、68 MPa 时涵身最大应力、涵顶土压力和活载挠度,见图11。可见:随着填土弹性模量增大,管涵最大环向拉、压应力、涵顶土压力及活载挠度均减小;当填土模量较低时(6 ~ 17 MPa),随着填土弹性模量增大,波纹钢管涵最大环向拉、压应力及活载挠度快速减小;当填土模量较高时(17 ~ 68 MPa),波纹钢管涵最大环向拉、压应力及活载挠度减小速度减慢。这说明波纹钢管涵的应力状态对填土弹性模量非常敏感,填土密实度对于保证波纹钢管涵受力状态非常关键。
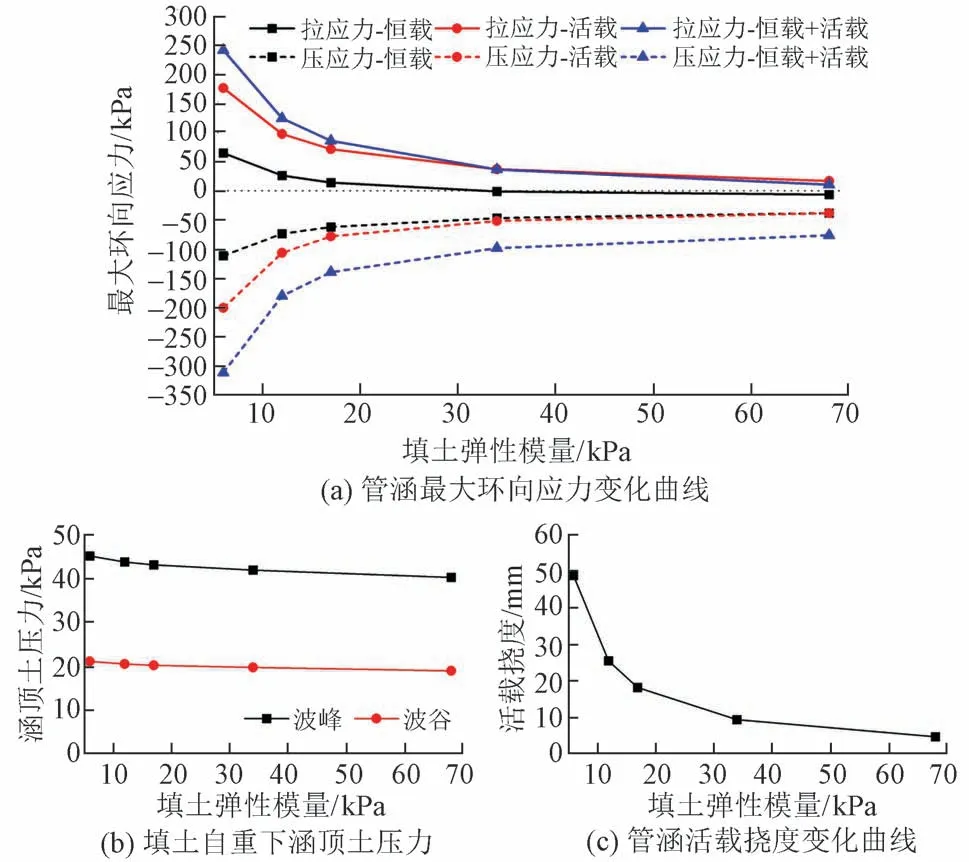
图11 不同填土弹性模量下管涵计算结果
3.4 管径
保持数值模型中其他参数不变,涵顶填土高度保持2 m,计算管径取1.0、1.5、2.0、2.5、3.0 m时涵身最大应力、涵顶土压力和活载挠度,见图12。可见:管径小于1.5 m 时,管涵最大环向拉、压应力随管径的增大而增加;在管径取1.5 m 时达到最大值,随后整体呈减小趋势,变化速率较慢。随着管径的增大,管涵涵顶土压力逐渐减小,管涵活载挠度基本线性增加。
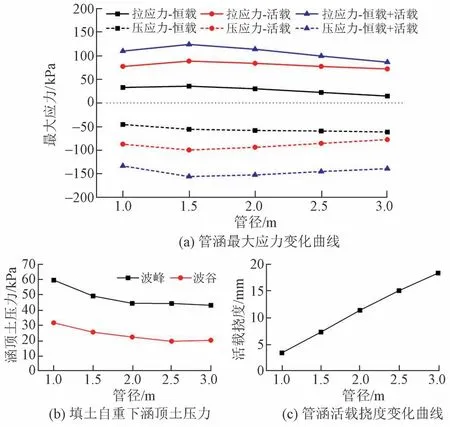
图12 不同管径下管涵计算结果
3.5 壁厚
保持数值模型中其他参数不变,计算壁厚取2、3、4、5、7、10 mm 时涵身最大应力、涵顶土压力和活载挠度,见图13。可见,随着壁厚的增大,管涵最大环向压应力减小,且减小速度先快后慢;涵顶土压力缓慢增大;管涵活载挠度基本线性减小。
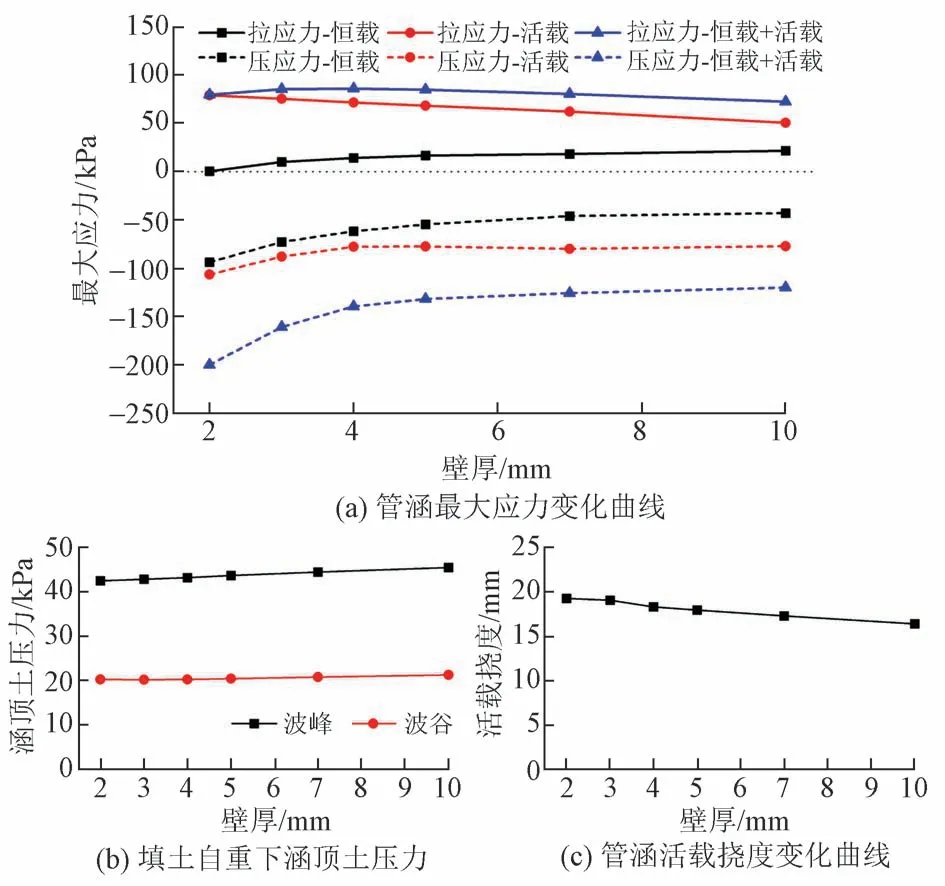
图13 不同壁厚下管涵计算结果
3.6 波形
保持数值模型中其他参数不变,计算波形取125 mm × 25 mm、150 mm × 50 mm、200 mm × 55 mm(截面惯性矩分别为357、1 459、1 819 mm4/mm)时涵身最大应力、涵顶土压力和活载挠度,见图14。可见,随着波形截面惯性矩的增大,管涵最大环向拉、压应力逐渐增大。波峰、波谷涵顶土压力平均值随波形截面惯性矩缓慢增大。随着波形截面惯性矩的增大,波纹钢管涵活载挠度基本线性减小。
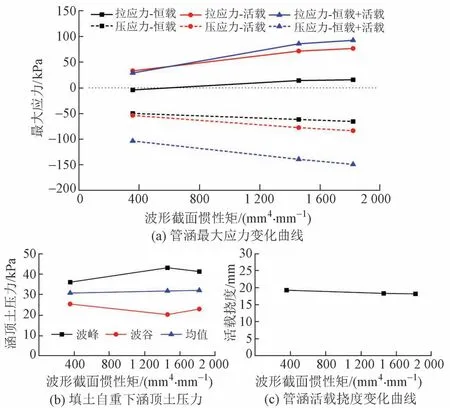
图14 不同波形下管涵计算结果
分别采用等截面面积和等截面惯性矩的圆管涵替代波纹钢管涵进行受力计算。管涵截面信息和模型计算结果见表2。可见,与等截面惯性矩的圆管涵相比,圆管涵和波纹管涵受力均表现为以弯曲应力为主导,波纹钢管涵环向压、拉应力增大109%、117%,活载挠度增加5.2%,但截面面积减小81%。等截面面积替换时,圆管涵截面惯性矩很小,截面上应力整体表现为压应力。与等截面面积圆管涵相比,波纹管涵活载挠度减小5.7%,压应力增大175%。与等截面面积圆管涵相比,波纹钢管涵环向受力状态理论上不具优势,其力学优势主要体在轴向变形能力强,且具有较大的截面弯曲刚度,便于施工。

表2 管涵截面信息和模型计算结果
4 结论
1)波纹钢管涵在承受整体环向压应力的同时,在涵顶、涵底和管涵两侧存在显著的弯曲应力,管涵最大绝对值应力为压应力;涵顶、涵底的波峰受压,波谷受拉,管涵两侧波峰受拉,波谷受压。
2)涵顶填土高度直接影响管涵的恒载土压力水平和活载扩散作用。土体弹性模量、管径、波形、壁厚对土体、管涵及二者的相对刚度有影响,进而影响管涵、土体之间的荷载分配及管涵的应力水平。
3)活载中心作用于接近管涵边界或管涵正上方和边界之间某位置时,管涵会取得最大环向压应力,但数值与活载中心作用于涵顶正上方时相差较小,不超过6.8%。

